直流电机调速的MCP-PID控制

方文阳，杨 平（上海电力学院 自动化工程学院，上海　20090）

直流电机调速的MCP-PID控制

方文阳，杨 平
（上海电力学院 自动化工程学院，上海20090）

针对快响应的直流电机调速过程，进行了MCP-PID控制器设计和仿真试验研究。直流电机调速过程的MCP-PID控制与ZN-PID控制的仿真试验结果表明：MCP-PID控制具有超调量小、调整时间短和鲁棒性高的优点。

直流电机；调速；MCP-PID控制；鲁棒性

0　引言

直流电机具有构造简单、使用方便、调速性能优秀等特点，在各个行业中得到广泛的应用。虽然近年来交流电机调速也发展很快，但是在机器人领域和在伺服控制领域，直流电机调速仍占主导地位。所以直流电机调速的深入研究还在继续。直流电机的控制一直以PID控制为主流技术［1］。因此，PID控制器的参数整定方法倍受关注。文献［2］提出了一种新的PID控制参数整定方法，采用该方法整定的PID控制器被称为MCP-PID控制器。MCP-PID控制器的参数整定依据一种称为多容惯性（MCP：multiple Capacity Process）标准传递函数，该传递函数被证明具有无超调、不限系统阶数和不限系统型次的优良特性［3］。文献［4～6］给出了MCP-PID控制器分别用于电站锅炉汽温过程、双容时滞过程和过热汽温串级过程的应用案例，结果表明MCP-PID控制具有超调量小、调整时间短、扰动抑制强和鲁棒性高的特点，值得在复杂工业过程控制系统中推广应用。但是，文献［4-6］的应用案例都是典型的慢响应过程控制类型，如果是用于电机调速一类的快响应过程控制案例，结果将怎样呢？这正是开展以下案例研究的初衷。

1　PID系统的性能

PID控制系统的性能主要取决于PID控制器参数的整定。因此，PID控制器的参数整定技术成为PID控制器实施成功的关键。自从 1942年 Tayor公司的 J.G. Ziegler和N.B.Nichols提出Ziegler-Nichols整定准则（简称Z-N整定法）后，就再没有更有影响力的PID控制器参数整定方法出现。不过，Z-N整定法是以实现衰减率为1/ 4动态性能为整定目标的方法。按Z-N整定后的控制系统必然有反应快但超调量大的特征。这对于要求反应缓而超调量小的控制系统就不适合。文献［2］提出的PID控制器参数整定方法则以超调量小和鲁棒性高为特征。按照文献 ［2］提出的整定方法整定的PID控制器，被称为MCP-PID控制器，而按照Z-N整定法整定的PID控制器将称为ZN-PID控制器。

根据文献［2］，MCP-PID控制器的参数整定原理可以简述为：针对单容时滞型或积分时滞型被控过程模型采用PID型控制器构成的PID控制系统，可推导出其闭环传递函数，令其规范后的特征多项式与MCP标准传递函数系统的同阶特征多项式相等，可解出PID控制器参数。由具有无超调量、调整时间短和鲁棒性高特性的MCP标准传递函数确定的PID控制器参数，自然继承了MCP标准传递函数的优秀动态性能。但是由于只做到了最优极点匹配而不配置零点，所以所整定的PID控制系统具有超调量小的性能而不保证无超调量。

图1　PID控制系统Fig.1 A PID control system

2　MCP-PID控制器及ZN-PID控制器设计

设典型的PID控制系统如图1所示。其中Gp（s）为被控过程的传递函数模型；Gc（s）设为常用PID控制器，其传递函数模型设计为：

若取PID控制器为文献［2］提出的MCP-PID控制器，则该控制器的参数整定计算如式（2）所示。若取PID控制器为常规的PID控制器，则常用Ziegler-Nichols整定法确定PID控制器参数。这里不妨称该类型PID控制器为ZN-PID控制器。根据文献［7］，当时，ZN-PID

控制器参数整定计算如式（3）所示。无论是MCP-PID控制器还是ZN-PID控制器，参数整定计算都依据的是单容时滞型被控过程模型（仅就有自平衡过程而言），如式（4）所示。

3　直流电机调速过程模型及PID控制器设计

3.1直流电机调速过程数学模型

根据文献［8］，可得到直流电机的传递函数形式的数学模型为：

式中：Ce—电势常数；Td—机电时间常数；Tm—电磁时间常数。假设以下的研究以文献［9］中的某大型直流电机为案例，该直流电机额定技术参数见表1，则可算得该直流电机的具体数学模型为：

表1　某直流电机额定技术参数Tab.1 The nominal technical parameters for the DC motor

3.2直流电机调速PID控制器设计

针对式（6）所示的具体被控过程，为设计MCP-PID控制器和ZN-PID控制器，还需要先得到式（6）模型相对应的单容时滞模型。为此，可通过Matlab的SIMULINK仿真平台先做得式（6）模型的阶跃响应曲线，再通过文献［10］介绍的两点法图解计算得到单容时滞模型参数如式（7）所示。从图2可看出，除了阶跃响应的初始时段，所拟合得到的单容时滞模型的阶跃响应曲线与原模型式（6）的阶跃响应曲线几乎重合。

图2　直流电机阶跃响应及拟合模型响应曲线Fig.2 The step responses of the DC motor and its fitted model

利用所拟合出来单容时滞模型参数，可分别算得MCP-PID控制器和ZN-PID控制器参数，见式（8）和式（9）。

4　仿真试验

4.1设定值跟踪与过程扰动抑制试验

利用Matlab的Simulink仿真平台可搭建直流电机调速控制系统的仿真试验模型，如图3所示。图中，上边的控制回路是直流电机调速的MCP-PID控制回路，下边的控制回路是直流电机调速的ZN-PID控制回路。Step模块产生设定值单位阶跃信号。Step1模块在t=0.5s时加入20%阶跃扰动信号。

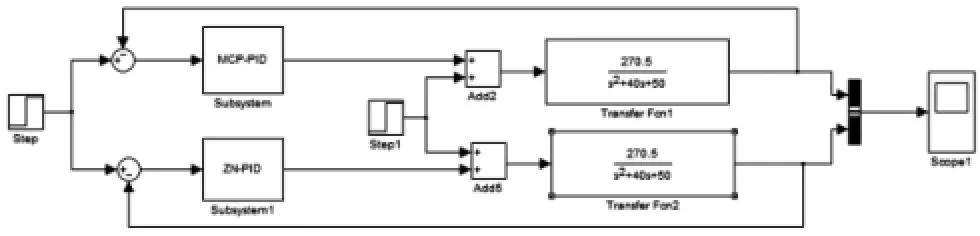
图3　直流电机调速控制的仿真试验系统Fig.3 The simulation test system for the DC motor speed control

Simulink仿真试验结果如图 4所示。可以看出，MCP-PID控制响应的最大超调量比ZN-PID控制响应的更小；在抑制扰动方面则是，MCP-PID控制略逊色于ZN-PID控制。

图4　直流电机调速控制系统响应曲线Fig.4 The step responses for the DC motor speed control system

4.2控制系统鲁棒性试验

在直流电机运行过程中，因环境影响或机身发热会使其电枢回路电阻的阻值发生变化。根据文献［8］和文献［9］，电枢回路电阻阻值的变化势必会影响直流电机的动态性能并使其数学模型参数发生变化。根据文献［8］，电枢回路电阻Rd的变化会使电磁时间常数Td和机电时间常数Tm发生变化，与电势常数Ce和转矩常数Cm无关，其相互关系如式（11）和式（12）所示。其中，Ld为电枢回路电感；GD2为飞轮转矩；Ce为电势常数；Tm为机电时间常数；Td为电磁时间常数。

为测试控制系统的鲁棒性，设置直流电机的电枢回路电阻Rd做增减变化：① Rd阻值上升20%；②Rd阻值下降20%。按式（4）计算可得，Rd阻值上升20%时的直流电机数学模型为式（13）；Rd阻值下降20%时的直流电机数学模型为式（14）。

利用图3所示的直流电机调速控制系统的仿真试验模型，分别进行电枢回路电阻Rd增减变化时的MCPPID控制和ZN-PID控制仿真试验，可得图5所示的仿真试验结果。对该结果的分析表明：①Rd阻值上升20%

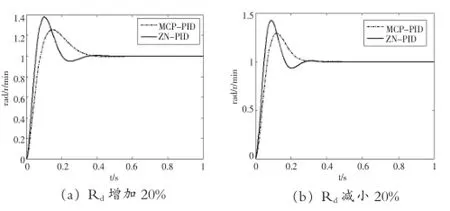
图5　Rd变化后的控制效果对比Fig.5 The control effect comparison with Rdchanging

时，MCP-PID控制响应的最大超调量σ%=25.69%，调整时间ts=0.335s；ZN-PID控制响应的最大超调量σ%= 37.97%，调整时间ts=0.311s；②Rd阻值下降20%时，MCP-PID控制响应的最大超调量σ%=28.41%，调整时间ts=0.283s；ZN-PID控制响应的最大超调量σ%=42.81%，调整时间ts=0.253s。将电枢回路电阻Rd增减变化仿真试验数据与电枢回路电阻Rd不变时仿真试验数据一起整理并对比分析可得鲁棒性特性分析表，见表2。

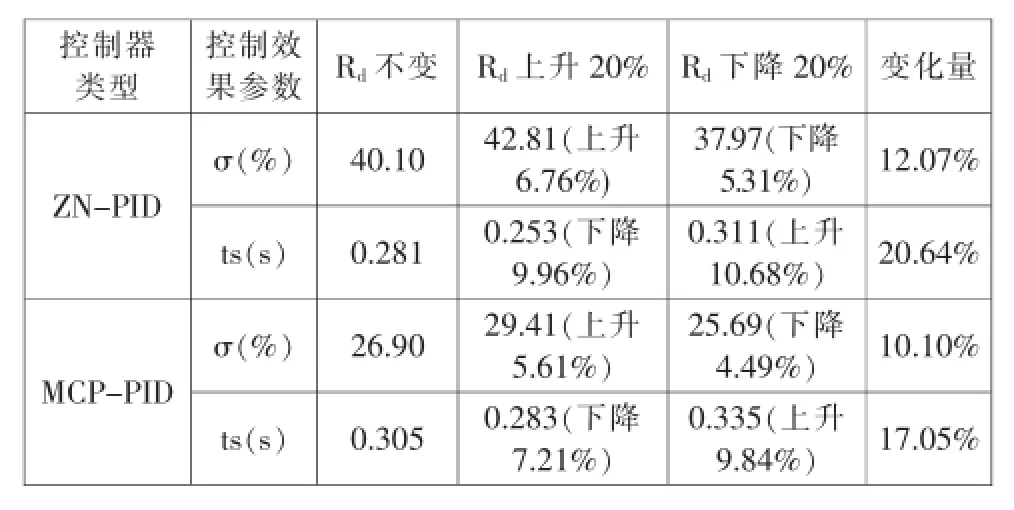
表2　MCP-PID控制和ZN-PID控制的鲁棒性试验结果分析Tab.2 The analysis of the robust tests for MCP-PID and ZN-PID

由表2可知，阻值从上升20%至下降20%变化时，MCP-PID控制的最大超调量的变化量为10.1%，而相应的调整时间的变化量为17.05%；而ZN-PID控制对应的最大超调量的变化量为12.071%，5结论

调整时间的变化量为20.64%。很明显，MCP-PID控制系统比ZN-PID控制系统具有更强的鲁棒性。

综上所述，针对快响应的直流电机调速控制过程，MCP-PID控制较常规PID控制有超调量小和调整时间短的优势，尤其在鲁棒性方面，MCP-PID控制可允许的系统参数变化范围远宽于常规PID控制。因此，MCPPID控制在直流电机调速领域有推广应用价值。

［1］王立涛.直流电机PID控制系统仿真研究［J］.电子设计工程，2012，18. ［2］杨平，黄伟，孙宇贞，等.PID参数整定的MCP标准传递函数法公式［J］.上海电力学院学报，2014，1.

［3］杨平.多容惯性标准传递函数控制器—设计理论及应用技术［M］.北京：中国电力出版社，2013.

［4］丁远扬，杨平.基于MCP-PID控制器的电站锅炉汽温控制［J］.电力科学与工程，2014，11.

［5］雷晓春，杨平.双容时滞过程的MCP-PID控制［J］.工业仪表与自动化装置，2014，5.

［6］苏隽成，杨平.过热汽温串级MCP-PID控制［J］.自动化仪表，2014，11.

［7］杨平，翁思义，王志萍.自动控制原理－理论篇（2版）［M］.北京：中国电力出版社，2014.

［8］张红莲，王丽玲，刘崇伦，等.电机与电力拖动控制系统［M］.北京：机械工业出版社，2013.

［9］张学阳，盛子怡，曾培煌.基于模糊参数自整定的双闭环直流电机调速系统研究［J］.机电产品开发与创新，2013，5.

［10］王再英，刘淮霞，陈毅静.过程控制系统与仪表［M］.北京：机械工业出版社，2006.

MCP-PID Control for a DC Motors Speed Regulation System

FANG Wen-Yang，YANG Ping
（Shanghai University of Electric Power，College of Automation Engineering，Shanghai 20090，China）

A study is conducted to design the MCP-PID controller with simulation for fast response DC motor speed control process.Comparing ZN-PID control with MCP-PID control，the simulation results show that MCP-PID control has small overshoot，shorter adjustment time and higher robustness.

DC motor；speed regulation；MCP-PID control；robustness

TH-39

Adoi：10.3969/j.issn.1002-6673.2015.05.036

1002-6673（2015）05-097-04

2015-07-14

项目来源：上海市电站自动化技术重点实验室（13DZ2273800）；上海市科技创新行动计划（13111104300）

方文阳（1992-），男，广西人，在读本科生。研究方向为电机先进控制；通讯作者：杨平。