航天器火工作动装置流固耦合过程的数值研究
2015-10-29杨震春杜永刚刘轶鑫
水 龙,杨震春,杜永刚,杨 勇,刘轶鑫
(兰州空间技术物理研究所 真空技术与物理重点实验室,兰州 730000)
航天器火工作动装置流固耦合过程的数值研究
水龙,杨震春,杜永刚,杨勇,刘轶鑫
(兰州空间技术物理研究所 真空技术与物理重点实验室,兰州730000)
航天器上配备的火工作动装置用于完成关键程序动作与任务,具有很高的可靠性与安全性要求。针对复杂结构火工作动装置的工作过程,建立非线性流固耦合动力学模型,在推力与拉力负载两种工况下,采用有限体积法、有限元法进行数值计算,得到火工作动装置工作过程中流场变化规律与输出性能。数值模拟结果表明,航天器火工作动装置流固耦合过程的数值分析能够模拟其工作过程,火工作动装置的负载对输出性能有较大影响。
航天火工装置;流固耦合;有限元;ALE方法
0 引言
航天器入轨后始终运行在真空环境中,通常配备有多个火工作动装置,以完成关键程序动作与任务[1]。火工作动装置以装药燃烧产生的高温高压气体作为驱动源,将化学能转化为机械能并输出线性作动力。在实际工程应用中,对火工作动装置具有很高的可靠性与安全性要求,且需要考虑到火工冲击对航天器结构的影响。火工作动装置的设计主要依赖工程经验,一般研制程序为经验/半经验设计-大量试验-改进设计。由于火工作动装置关键参数的微调能对输出性能产生巨大影响[2],实际研制过程中总是需要进行大量试验与反复修改设计,导致研制周期长、成本高。另一方面,由于火工作动装置的体积较小、工作时间极短(毫秒级),对其工作过程性能的全面测试有较大困难。因此,为了提高火工作动装置的设计水平、缩短研制周期、降低研制成本、全面而准确获得其工作过程性能,对火工作动装置工作过程进行数值模拟是十分必要的。
20世纪50年代末,美国、俄罗斯就开始在航天器上采用各种火工装置,已积累了丰富的工程经验,并进行了一定的相关理论研究。1993年,Kuo等[3]分析了由NASA标准电起爆器驱动拔销器的动态特性,分别采用C语音、MESA-2D代码程序建立了两个理论分析模型,分析结果能与试验数据更好地吻合。此后,Goldstein等[4]采用NASA-2D和DYNA 3D软件对拔销器和电爆阀门的工作过程进行了动力学仿真分析,为结构受力和变形的研究提供了依据。1994年,Gonthier等[5-6]以NASA标准电起爆器驱动的拔销器为研究对象,采用LSODE标准程序对所建立的理论模型进行求解计算,对该拔销器火药(Zr/KClO4)燃烧过程、活塞运动过程进行了分析。美国的一些专业火工装置生产厂也开发了自己的性能分析和模拟手段[7],如Scot公司能够对火药燃烧过程、分离作动过程、温度、压力等进行计算机模拟仿真,并进行设计优化。
南京理工大学的王涛等[8]基于经典内弹道和气体动力学理论,建立了二级活塞式抛放弹射机构的理论模型,采用Godnov差分格式对该弹射机构的工作过程进行了数值模拟计算,分析了不同参数对其弹射效果的影响。高滨[7,9]基于经典内弹道理论,建立了火工作动装置的性能计算模型,利用性能仿真模型对一种弹射装置进行了分析,计算结果与试验结果基本吻合。北京理工大学的叶耀坤等[10]对一种用于高速导弹分离系统的楔块式火工解锁螺栓动作过程建立了内弹道模型,并利用MATLAB/Simulink进行了仿真计算,可以反映该火工解锁螺栓的分离运动特性。综上所述,火工作动装置的仿真分析模型关注火药的燃烧过程,采用牛顿第二定律描述活塞的运动过程,均没有考虑火工作动装置工作过程中的非线性流固耦合等本质特性。
针对火工作动装置工作过程中的非定常、高速可压缩高温高压气体与活塞之间的非线性流固耦合问题,以伸长型火工作动装置为研究对象,引入任意拉格朗日-欧拉(ALE)方法描述流场控制方程,建立火工作动装置工作过程的流固耦合系统动力学模型。在不同负载工况条件下,结合有限体积法与有限元法进行求解计算,获得火工作动装置的流场变化规律、活塞运动位移和速度等输出性能。
1 流固耦合系统动力学模型的建立
火工作动装置燃烧室内火药燃烧产生的高温高压气体流经腔室后作用于活塞,活塞克服负载开始运动,输出满足要求的推力,如图1所示。火工作动装置的工作过程是一个复杂的物理、化学变化过程[7],工作时间极短,涉及到高温高压气体的超音速流动、几何非线性(活塞的大位移运动)、状态非线性(筒壁与活塞的接触)、流固热多场耦合等重要问题,这是一个强瞬时性、强非线性和强耦合的复杂系统。对火工作动装置工作过程性能的数值模拟实质就是非线性流固热耦合系统动力学建模及其求解问题。
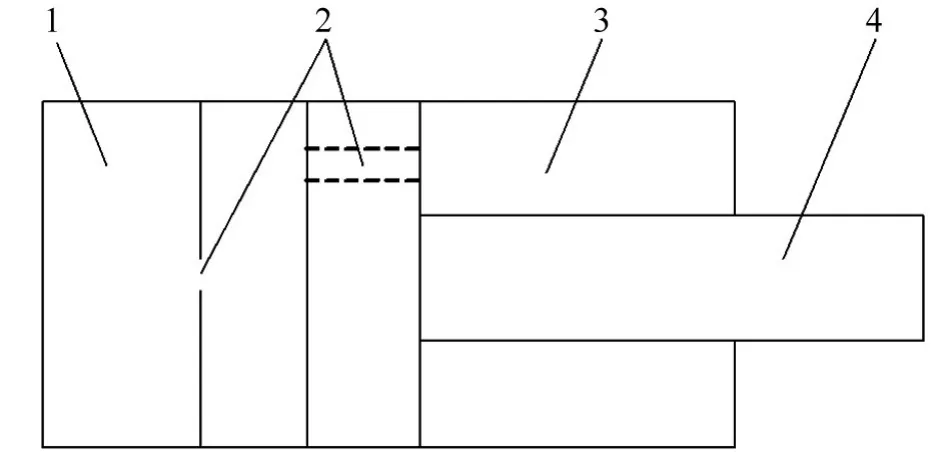
图1 火工作动装置工作原理图
1.1非线性偏微分方程组
给出三个假设条件:(1)火药燃烧产生的高温高压气体为三维非定常、高速可压缩流动气体;(2)关于任一单元体,高温高压燃气满足完全气体状态方程;(3)整个工作过程忽略热量损失。
建立笛卡尔坐标系O-xyz,对于流场内任意一点(x,y,z),在t时刻的速度为v=[u v w]T,密度为ρ,压力为p,温度为T;流体的分子粘性系数、第二粘性系数分别为ρ、λ,热传导系数为k,单位质量的体积力为f,通过表面的热通量为q,单位质量的体积加热率为r˙,单位质量的内能为e。根据质量守恒、动量守恒以及能量守恒定律,可以分别得到连续性方程、动量方程与能量方程为:
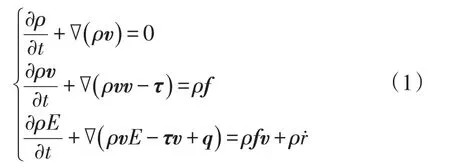
这一组控制方程就是守恒形式的纳维-斯托克斯(N-S)方程,写成更简洁的形式为:
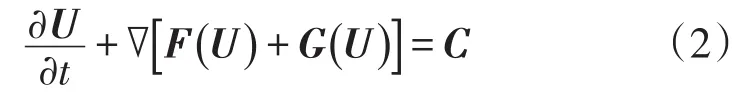
火工作动装置内火药燃烧产生的高温高压气体作用于活塞,高温高压燃气流场的变化影响活塞的变形和运动,而活塞的变形和运动又会影响燃气流场的变化[11]。由于火工作动装置活塞的运动会导致流场网格的运动,这里采用任意拉格朗日-欧拉(ALE)方法来描述网格的几何变形与运动。
流场中任一控制体V的控制面为S,控制面的外法向矢量为S,在t时刻动网格的运动速度为w。
将式(2)写成在ALE坐标系中的积分形式:
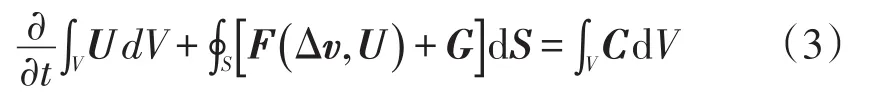
式中:Δv=v-w。
为了得到封闭方程组,补充气体状态方程:
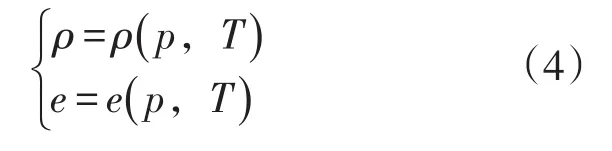
联立式(3)、(4),得到一组非线性耦合偏微分方程组,该方程组的求解变量为守恒变量U。
1.2边界条件和初始条件
火工作动装置非线性流固耦合系统包括三个求解域:火药燃烧产生高温高压气体形成的流场,火工作动装置的筒壁与活塞形成的结构场,流场与结构场的耦合界面。火工作动装置在工作过程中,其流场各点的速度、压力、温度等变量之间是强耦合关系,每个边界条件都需要对变量进行综合考虑。注意到火工作动装置的对称性,取原模型的1/2作为分析模型,并在截断面上施加对称边界条件。定义火工作动装置的筒壁作为高温高压流场的固定壁面,并采用无滑移条件,即气体在筒壁上的速度v=0,忽略热量损失。定义气体与活塞界面为流固耦合边界,该边界需要同时满足运动学与动力学条件,实现流场与结构场的耦合。结构场内在火工作动装置的筒壁与活塞之间定义接触面,在活塞端部施加与实际情况符合的负载,并定义与流场相对应的流固耦合边界条件。边界方程离散化后,可以整合到系统动力学模型中进行求解计算。
根据火工作动装置的装药结构,分别定义火药组与空气组的初始条件,可以模拟火药瞬间燃烧产生高温高压燃气的过程。
因此,采用ALE方法描述了火工作动装置内流场、流场与结构场的耦合过程,并给出流固耦合过程的边界条件和初始条件,得到火工作动装置非线性流固耦合系统的动力学模型。
2 流固耦合系统的求解
对于前面得到的流固耦合系统动力学模型,是一个强非线性、强耦合复杂系统,无法直接得到其解析解,结合有限元法和有限体积法进行数值求解,得到变量的变化规律。
对火工作动装置的结构域、流场域离散化。火工作动装置的筒体与活塞结构复杂,均采用四面体单元进行自由网格划分;流场域与结构域互补,也采用四面体单元进行网格划分。如图2所示,每个四面体单元包含4个控制体、4个节点。

图2 四面体单元网格划分图
取时间步长为Δt,对时间项的积分采用欧拉方法,取积分参数α=1。流场内任一控制体V,对式两边进行积分,并将积分项用平均值表示,整理后可得:
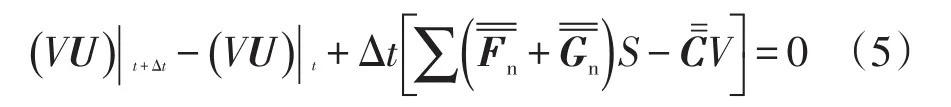
式中:Fn是矢通量F在法矢量n方向的分量,即Fn= nF;同理,Gn=nG。
下面采用有限体积法求解包含对流项和压力的非粘性项Fn,有限元法求解包含粘性和传导项的粘性项Gn。
2.1计算非粘性项
对于流场中某一单元体的一个面,定义该三边形的三个顶点分别为1、2、3,这三个顶点的位移为ri(i=1,2,3)、运动速度为wi(i=1,2,3)。于是有:
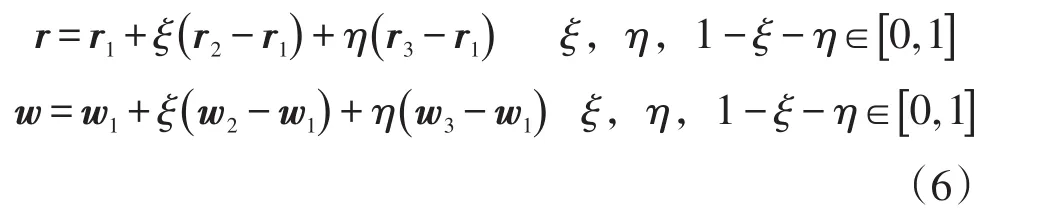
流场体积变量为:
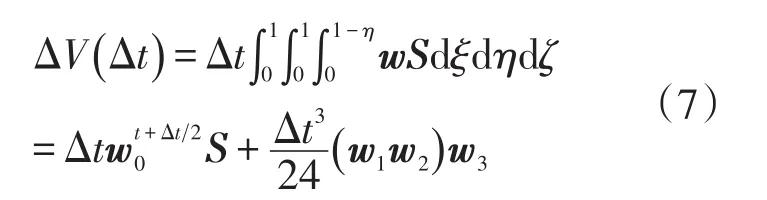
式中:w0=(w1+w2+w3)/3。
在t~t+Δt时间段内,该单元面的平均运动速度为:

分别用L、R表示共用一个单元面的两个控制体,Roe平均变量为:
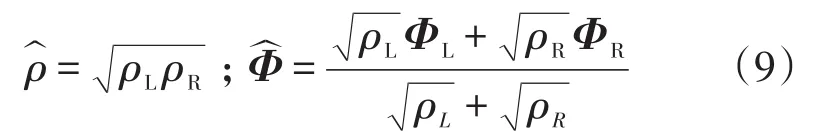
矢通量增量ΔF用Roe平均变量表示为:

式中:P、P-1为特征矩阵。
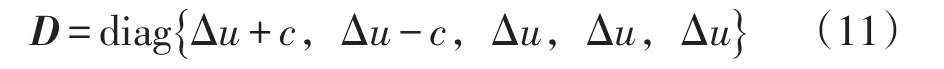
其中:Δu=u-wn,c为声速。
因此,平均非粘性矢通量为:
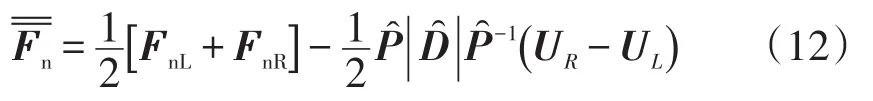
2.2计算粘性项
采用有限元法计算粘性项,关于控制体的面S积分有:

于是,热通量可用式(14)计算:

式中:hi为单元形函数。
2.3求解步骤
基于ALE描述的火工作动装置工作过程流固耦合系统有限元方程,结合有限体积法与有限元法进行数值计算。求解步骤为:
(1)对求解域内所有单元循环求解:
a.计算形函数及其导数;
b.对求解域内所有控制体循环求解:
c.结束控制体循环;
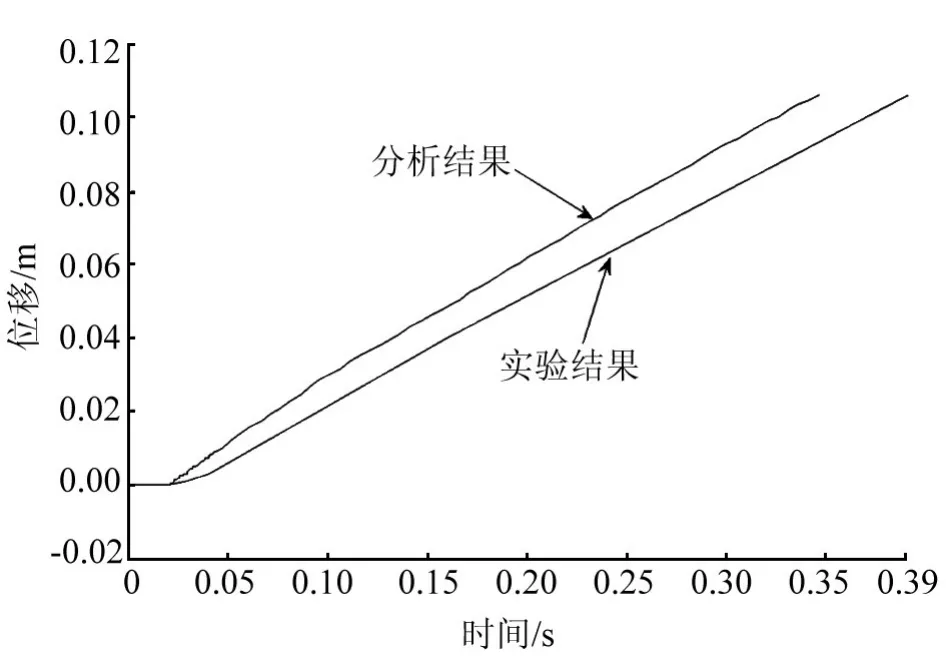
图3 工作过程中活塞的位移变化图
e.结束控制体面循环;
(2)结束单元循环。
3 结果与分析
建立火工作动装置的流场、结构场有限元模型,在结构场分别施加推力与拉力两种工况的负载,并进行直接耦合求解。值得注意的是,流场有限元模型的网格划分对计算效率和解的精度有直接关系,对计算收敛性有重要影响。
在推力负载作用下,火工作动装置工作过程中活塞的位移随时间的变化如图3所示,活塞的运动速度变化如图4所示。
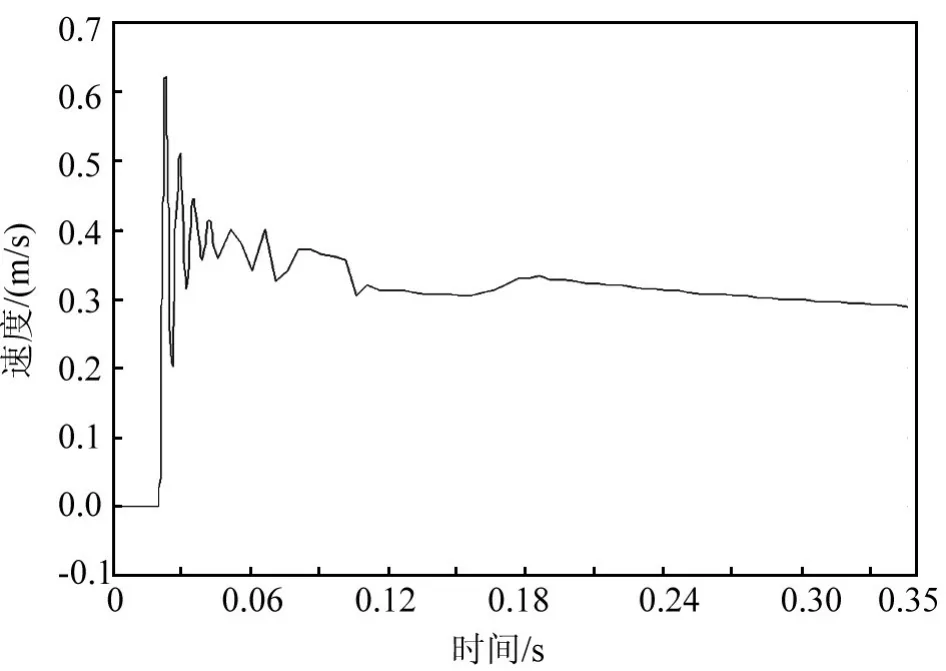
图4 工作过程中活塞的速度变化图
由图4可知,在点火后经过0.02 s,活塞开始运动,活塞的位移随着时间的增加而增加,且位移与时间近似呈线性关系;试验结果与分析结果基本一致,验证了仿真分析的正确性。活塞的速度先波动后趋于稳定,达到稳定状态后随着时间的增加逐渐减小。经过0.345 s后活塞运动到位,火工作动装置的行程为0.106 m,活塞的到位速度为0.29 m/s,活塞到位时会对筒体与周围结构产生较大冲击。
在火工作动装置腔室空间内取点1、点2、点3、点4以及点5,如图5所示。

图5 腔室空间内点的示意图
考察在火工作动装置工作过程中所选取各点压力、温度随时间的变化关系,分别如图6、7所示。
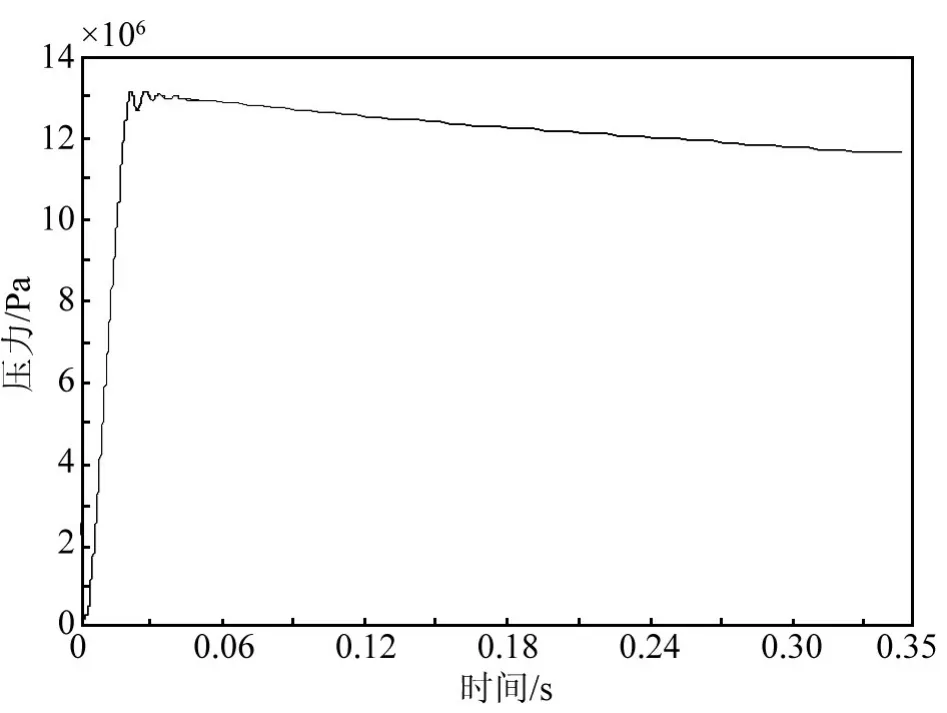
图6 腔室空间内各点的压力变化图
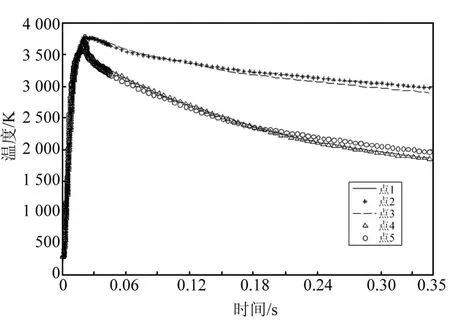
图7 腔室空间内各点的温度变化图
由图6可知,腔室空间内5个点的压力随时间的变化关系完全一致,腔室内压力先增大,经过较小波动后逐渐减小。在0.028 s时刻,腔室空间内压力达到最大值13.12 MPa。这5条完全重合的曲线说明,在火工作动装置工作过程的各个时刻,其腔室空间内各点的压力处处相等,即可以认为腔室空间内压力瞬时平衡。由图7可知,腔室空间内5个点的温度随时间的变化趋势是相同的,均先增大后逐渐减小,在活塞运动到位时刻,位于腔室空间后端的点2、点3的温度明显高于位于前端的点1、点4,腔室空间中间的点5的温度介于两者之间且靠近前端空间点。
在拉力负载作用下,火工作动装置工作过程中活塞的位移变化如图8所示,活塞的运动速度变化如图9所示。

图8 推力与拉力负载作用下活塞位移变化的对比图
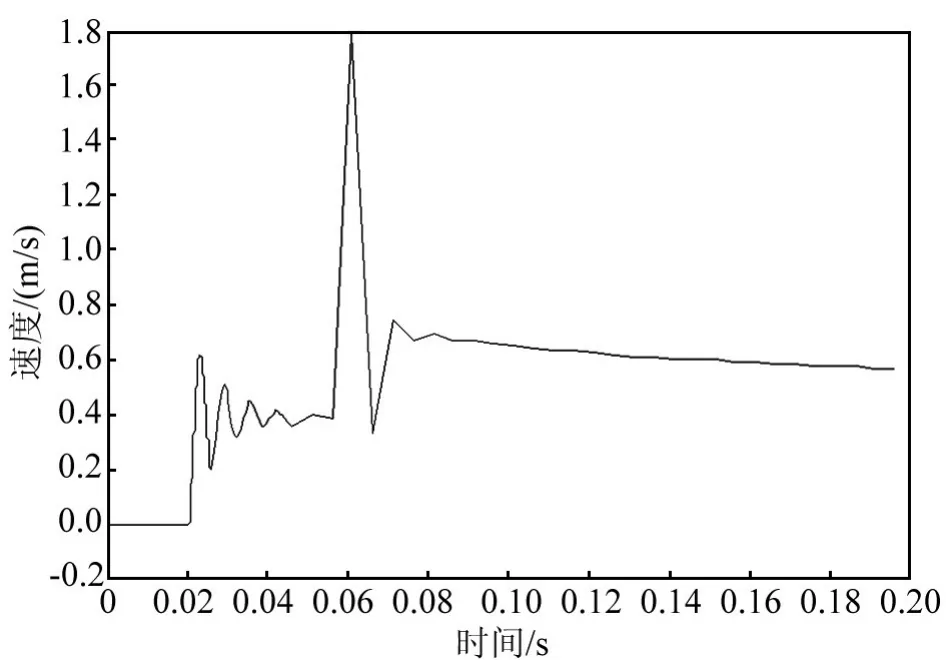
图9 拉力负载作用下活塞的运动速度变化图
由图9可知,与在推力负载作用下相同,点火后经过0.02 s,活塞开始运动,活塞的位移随着时间的增加而增加,且位移与时间近似呈线性关系;活塞的速度先波动后趋于稳定,达到稳定状态后随着时间的增加逐渐减小。经过0.196 s后活塞运动到位,火工作动装置的行程为0.106 m,活塞的到位速度为0.56 m/s。与推力负载作用下工况相比,受到拉力负载作用时,火工作动装置活塞的运动速度更快,到位时间更短。从图9可以看出,活塞的运动速度在经历波动后明显出现突然增大后突然减小的现象,这是由于活塞在与其运动方向相同的拉力作用下开始快速运动,火工作动装置通过调节给活塞一个反向作用力使得其运动速度减小,因此该火工作动装置具有较好的负载自适应性。另外,在拉力负载作用下,活塞到位时会对筒体与周围结构产生更大冲击。
4 结论
以复杂结构火工作动装置为研究对象,引入任意拉格朗日-欧拉(ALE)描述方法,建立了火工作动装置工作过程的非线性流固耦合动力学模型,采用有限体积法、有限元法进行了数值计算。计算结果表明:
(1)采用有限体积法、有限元法对火工作动装置的工作过程进行数值模拟是有效的,理论模型表征了火工作动装置工作过程的非线性流固耦合本质特征,通过求解计算得到了其流场变化规律与输出性能;
(2)火工作动装置在推力、拉力两种负载工况下,其输出性能基本保持一致,具有较强的负载自适应性;
(3)由于火工作动装置的体积较小,工作时间极短,工作过程中腔室空间内各点压力变化规律一致,可以认为腔室空间内各点压力是瞬时平衡的;
(4)火工作动装置活塞运动到位时,会对筒体产生较大冲击,进而对火工作动装置及其周围结构产生影响。因此,需要考虑采取相应的缓冲措施。
[1]王希季.航天器进入与返回技术(下册)[M].北京:中国宇航出版社,1991.
[2]Bement L J,Schimmel M L.A Manual for Pyrotechnic Design Development and Qualification[R].NASA Technical Memorandum110172,1995.
[3]Kuo J H.Dynamic analysis of NASA Standard Initiator driven pin puller[C]//AIAA,Joint Propulsion Conference and Exhibit,29th,Monterey,CA,1993.
[4]Goldstein S,Lu Y M,Wong T E.Importance of enhanced test dataforcomputermodelingofexposivelyactuateddevices[C]// AIAA,Joint Propulsion Conference and Exhibit,31 st,San Diego,CA,1995.
[5]Gonthier K A,Powers J M.Formulations,predictions,and sensitivity analysis of a pyrotechnically actuated pin puller model[J].Journal of propulsion and power,1994,10(4): 501-507.
[6]Gonthier K A,Kane T J,Powers J M.Modeling Pyrotechnic Shock in a NASA Standard Initiator Driven Pin Puller[R]. AIAA94-3054,1994.
[7]高滨.火工分离装置的性能研究[D].长沙:国防科学技术大学,2005.
[8]王涛,廖振强,贾安年,等.二级活塞式弹射机构动态仿真与分析[J].弹道学报,2002,14(4):36-39.
[9]高滨.火工作动装置设计参数的敏感性分析[J].航天返回与遥感,2006,27(3):57-59.
[10]叶耀坤,严楠.低冲击火工解锁螺栓的内弹道特性分析[J].北京工业大学学报,2012,38(9):1332-1336.
[11]邢景棠,周盛,崔尔杰.流固耦合力学概述[J].力学进展,1997,27(1):19-38.
NUMERICAL SIMULATION ON NONLINEAR FLUID-STRUCTURE INTERACTION PROCESS OF PYROTECHNICALLY ACTUATED MECHANISM
SHUI Long,YANG Zhen-chun,DU Yong-gang,YANG Yong,LIU Yi-xin
(Science and Technology on Vacuum Technology and Physics Laboratory,Lanzhou Institute of Space Technology and Physics,Lanzhou730000,China)
The pyrotechnically actuated mechanisms equipped on spacecraft are used for achieving key procedures and missions,and need to satisfy very high reliability and security requirements.This paper focused on the working process of pyrotechnically actuated mechanism with complex structure,the dynamics model considering nonlinear fluid-structure interaction has been established and solved by using finite volume method and finite element method under two different load working conditions.The change of variables in fluid field and output performance of pyrotechnically actuated mechanism has been obtained.The numerical simulation results showed the availability of numerical simulation on pyrotechnicallyactuatedmechanism,andtheoutputperformanceofpyrotechnicallyactuatedmechanismwas relatedtotheloads.
space pyrotechnic device;fluid-structure interaction;finite element analysis;ALE method
V423
A
1006-7086(2015)01-0042-06
10.3969/j.issn.1006-7086.2015.01.010
2014-10-28
水龙(1989-),男,硕士研究生,主要从事非线性多场耦合仿真研究工作。E-mail:shuilonghit@126.com。
