基于主成分分析和支持向量机的滚动轴承故障特征融合分析

古莹奎　承姿辛　朱繁泷

江西理工大学,赣州,341000

基于主成分分析和支持向量机的滚动轴承故障特征融合分析

古莹奎承姿辛朱繁泷

江西理工大学,赣州,341000

为有效降低滚动轴承故障特征的维数并提高诊断准确率，将主成分分析(PCA)和支持向量机(SVM)方法应用到轴承故障特征的融合分析中，给出了相应的决策流程。应用基于小波包分解的特征提取算法及特征向量的构造方法对不同状态下的振动信号进行分解，得到用于表征轴承运行状态的8维特征集合；应用PCA提取累积贡献率达到95%的特征主成分并输入SVM分类器中进行识别。结果表明，将滚动轴承故障特征从8维降低到5维，仍可有效表征轴承的状态，但大大降低了计算的复杂性；故障诊断的准确率达到97%以上，诊断时间也相对较短；4种轴承状态识别的准确率从高到低依次为正常、外圈剥落、滚动体剥落和内圈剥落，可为确保设备安全运行和快速故障诊断提供理论依据。

主成分分析;支持向量机;特征融合;故障诊断;滚动轴承

0　引言

在故障诊断中,如何尽可能多且准确地从信号中获取与设备状况相关的信息是基于振动信号进行故障诊断的关键[1]。任何一类诊断对象,单用一方面信息来反映其状态行为都是不完整的，仅依靠单一的理论方法和单一的故障信息也难以对故障作出精确的诊断。为对设备作出更准确、更全面的状态评估，需要从不同角度获取更多表征其运行状态的信息，但随着信息量的增大,急需解决的问题是如何充分地融合筛选信息并加以高效利用。

当前,神经网络、证据理论、互信息、支持向量机(support vector machine,SVM)等方法已被引入故障信息的融合中并得到有效应用。王赟松等[2]在发动机的故障诊断中用基于神经网络的特征层信息融合诊断取代单一传感器,有效地压缩了信息并实现了实时处理与诊断，取得了良好效果。Otman等[3]用基于信息融合的D-S证据理论对发动机进行了故障诊断。而针对传统D-S证据理论中存在的证据冲突等问题,Niu等[4]通过神经网络将多传感器收集信号进行特征级融合后，应用D-S回归和最小二乘SVM进行决策级融合，实现对压缩机的状态监测。Peng等[5]在将互信息理论用于特征选择方面做了大量的工作,使用互信息最大最小相关性的方法评价特征,通过互信息的大小判断特征之间的相似程度,认为相似程度高的特征携带的故障信号具有冗余性而予以剔除。李冰等[6]将互信息用于轴承振动信号特征参数集的优化选择。Zhao[7]运用基于粗糙集的特征选择方法和基于SVM的特征选择方法进行行星齿轮箱的故障诊断，在252种反映设备运行状态的特征中选择了10余种关键特征，从而避免了由于故障特征多而产生的分类器模型复杂和效率低等问题。蒋玲莉等[8]将SVM应用于多振动信息融合的齿轮故障诊断中。

以上方法尽管在故障特征的融合中得到应用，但随着信息量的增大，单一的方法仍然难以对信息进行有效的处理，尤其是当冗余信息较大时。本文以滚动轴承为研究对象，将基于主成分分析(principal component analysis，PCA)的特征级融合引入旋转机械的故障诊断，对轴承试验中由小波包分解所得特征进行融合，实现故障特征的降维，并结合SVM分类器良好的分类性能，使得输入到故障分类器的特征集更加简练高效，以降低分类器运行时间，减小计算量，通过对冗余信息的删除提高故障诊断的准确率。

1　PCA和SVM

PCA是一种分析、简化数据的技术，通过线性变换将问题从高维转化到低维，保留低阶主成分，删除高阶成分，达到降低数据集维数的目的。通过降维将原本复杂的多维数据转换成简单、直观且不相关的低维数据，有效降低数据分析的难度和复杂程度[9]。

将机械振动信号用模式向量矩阵表示为X=[x1x2…xn],其中第l列为Xl=[x1lx2l…xnl]T,xl表示设备的某一状态,其协方差矩阵为[10]

(1)

求矩阵Rx的特征值以及特征向量。将特征值λi(i=1,2,…,n)进行排序：λ1>λ2>…>λn，各特征值对应的特征向量为vi。样本xj投影到特征向量vi，得到该方法对应的主成分量为

(2)

所求特征向量构成n维正交空间,将样本投影到该空间即可得到对应的n维主成分量。重构时特征向量的贡献率与其所对应的特征值大小成正比。设正交空间中前l个主成分量为y1,y2,…,yl,其累积贡献率为

(3)

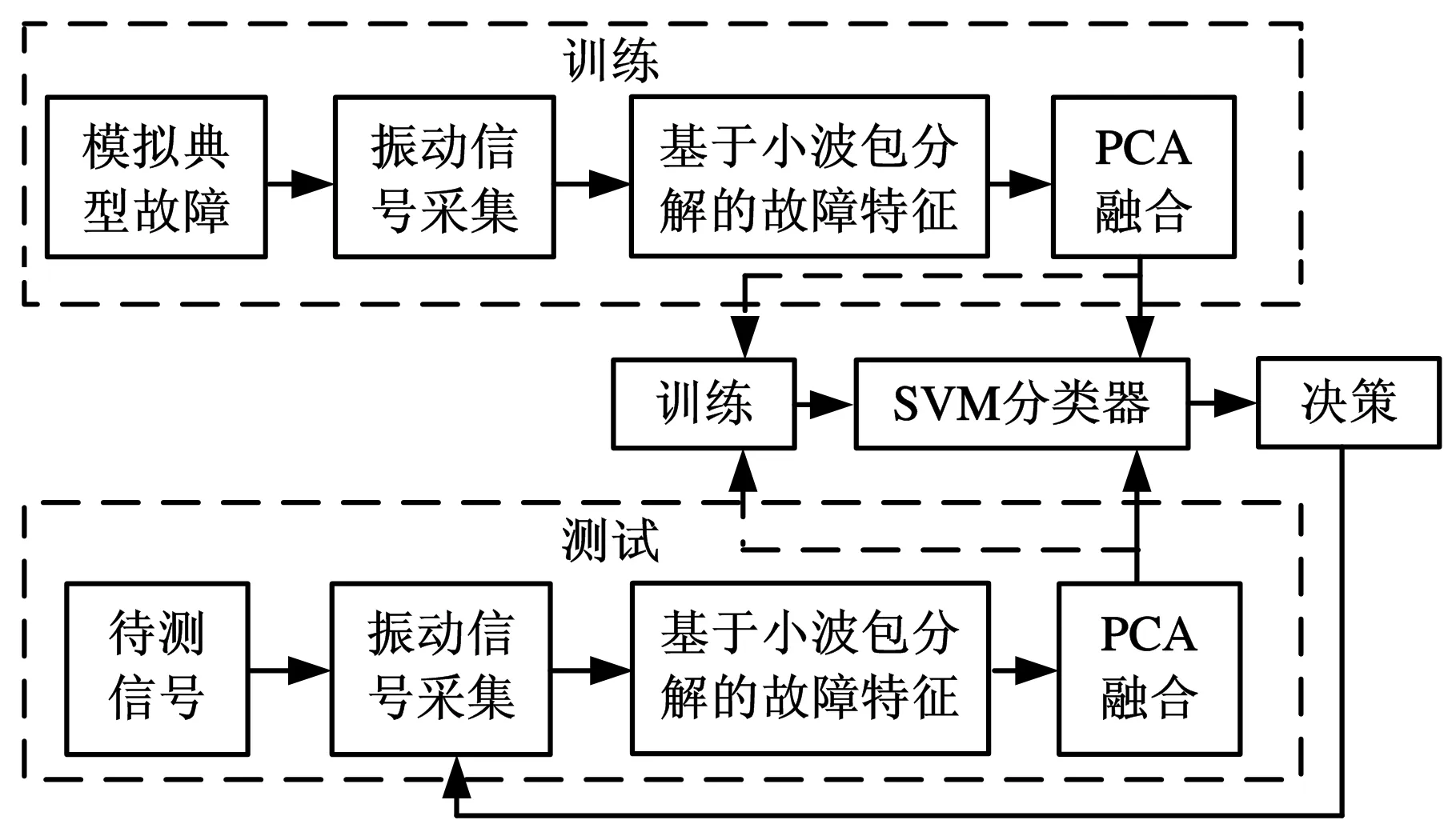
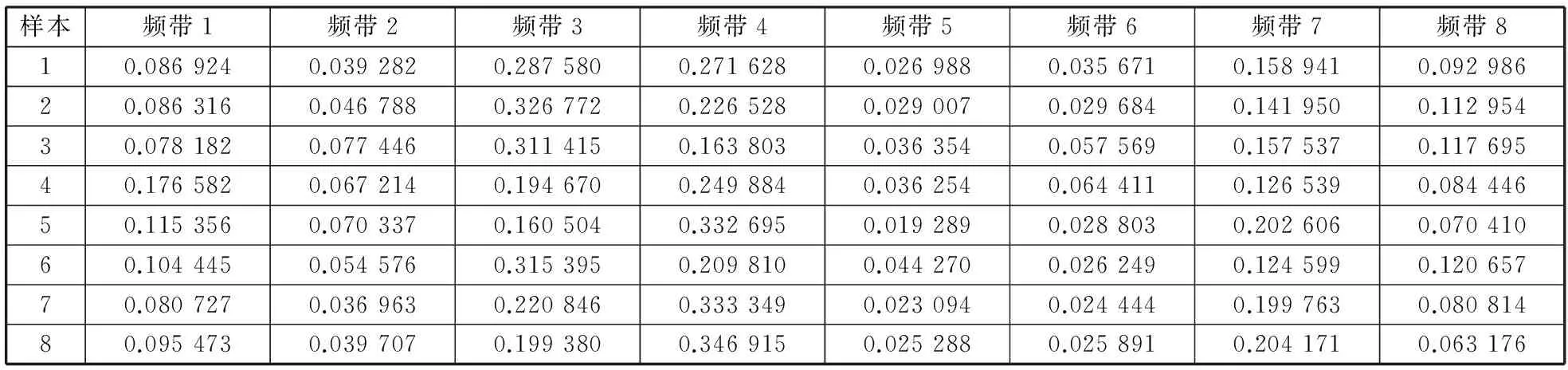
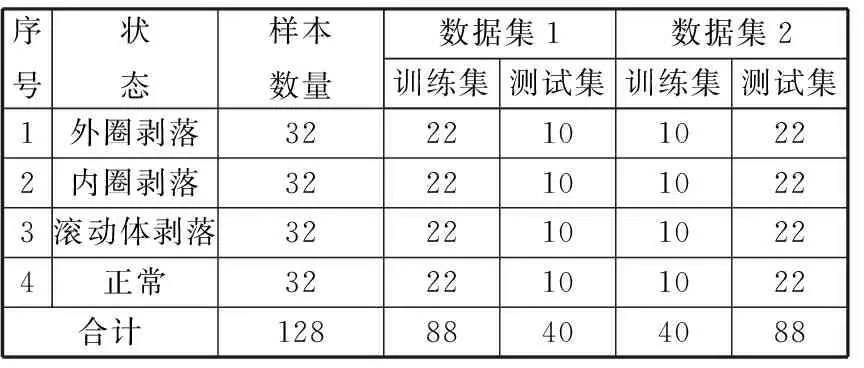
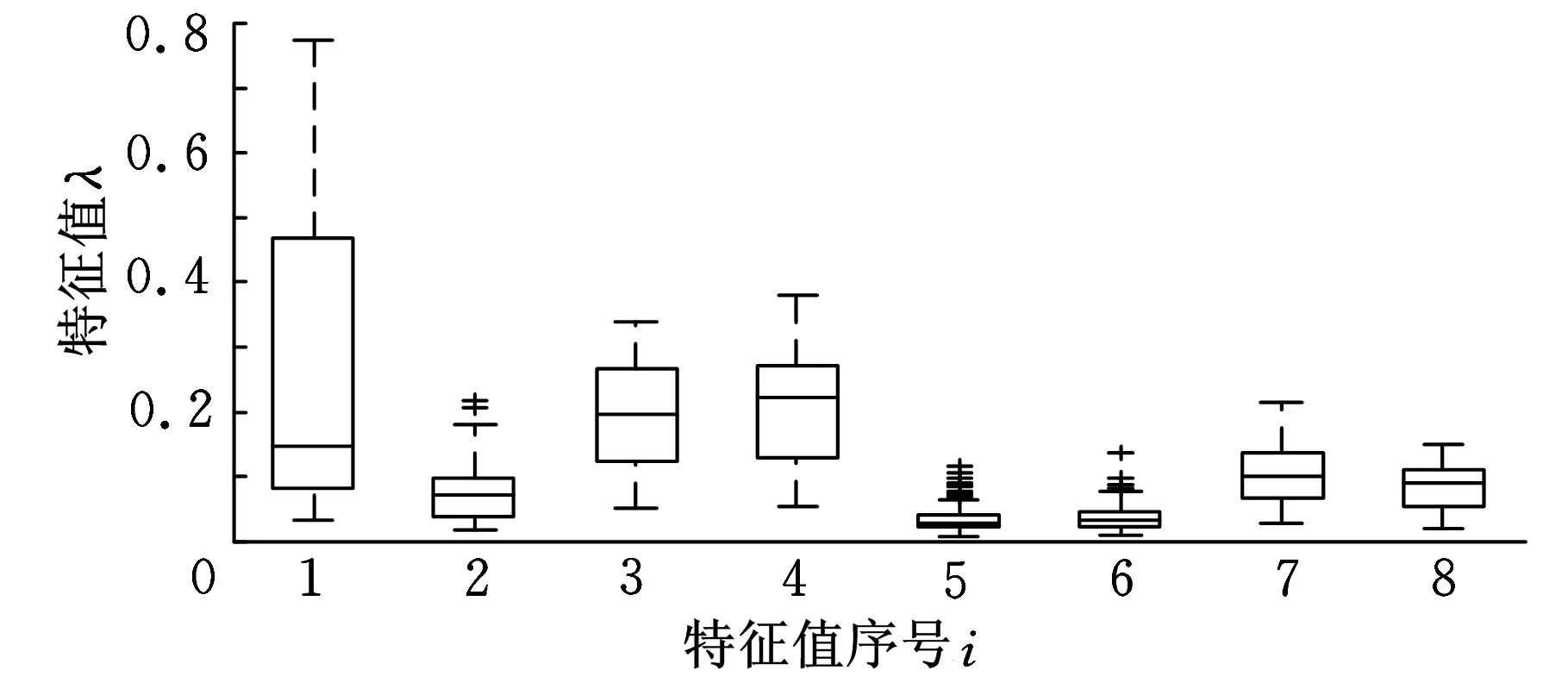
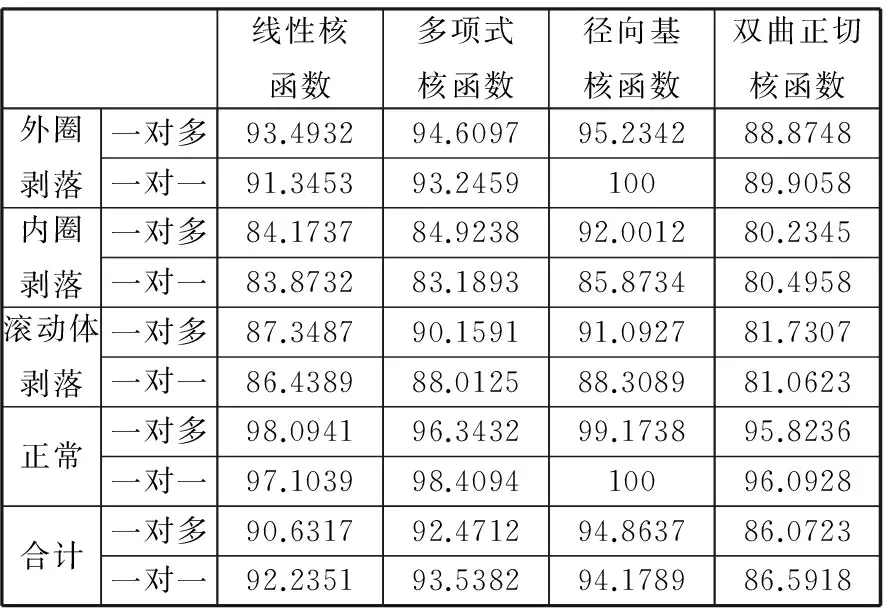
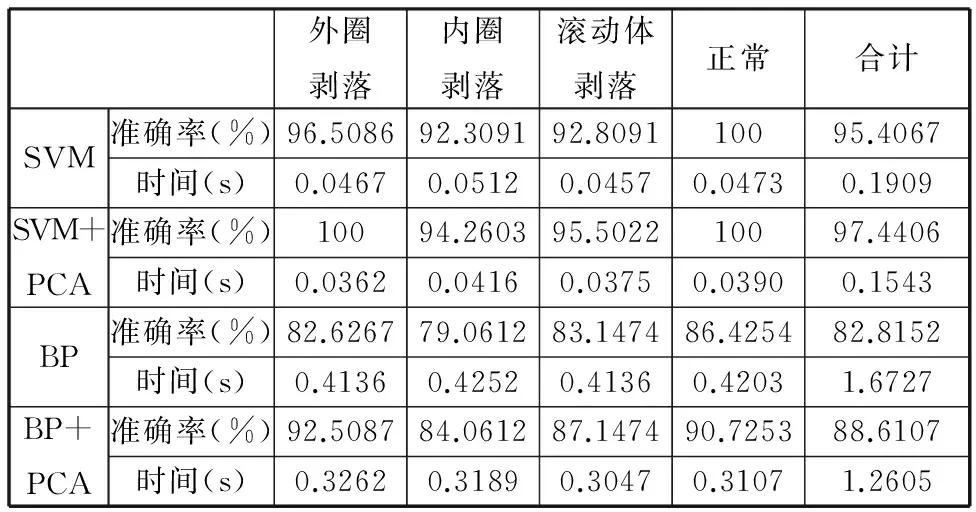
θ的取值通常在95%以上,即l(l

SVM是建立在统计学习理论基础上的一种数据挖掘方法，能非常成功地处理回归问题和模式识别等问题，可推广应用于预测和综合评价等领域。SVM的机理是寻找一个满足分类要求的最优分类超平面，使得该超平面在保证分类精度的同时，超平面两侧的空白区域最大化[11-12]。实质上，机械设备故障诊断是多类别模式识别和多值分类问题，设备故障类型和失效形式多种多样，其损坏的严重程度也有大小之分,因而,如何实现SVM分类器在多值分类中的应用是实现准确的故障特征分类与诊断至关重要的环节之一。目前，SVM处理多值分类问题使用最为广泛的算法有一对一算法和一对多算法[11]。

2　小波包故障特征提取算法及特征向量的构造

原始信号经小波包分解后得到具有一定能量的分解频带信号，可将各分解频带信号所携能量与信号总能量之比作为特征向量以表征设备的运行状态。

信号经小波包分解后所得分解频带相互独立且无冗余,由能量守恒定理可得[13]

(4)

设原始信号x(t)长度为N,分解频带离散信号xk,m(i)长度缩减为2-kN,其能量可表示为

(5)

归一化处理后,第m频带分解信号的相对能量可表示为

En(m)=En(xk,m(i))/En(x(t))

(6)

根据能量守恒原理,显然有

(7)

设备运行状态的改变使其振动信号各频带内信号能量随之发生变化,因此分解频带信号能量占总能量之比组成的特征向量e可很好地表征设备的运行状态,其表达式为

e=(En(xk,1(i)),En(xk,2(i)),…,

En(xk,m(i)))/En(x(t))

(8)

3　基于PCA与SVM的故障特征分类与诊断流程

根据PCA、SVM和小波包分解理论，结合机械故障诊断的特点，基于PCA与SVM的故障特征分类与诊断流程如图1所示。

图1　基于PCA和SVM的故障特征分类与诊断流程

在训练阶段,采集设备已知状态的振动信号，将振动信号进行小波包分解，求得用于表征已知状态的特征向量。利用PCA进行特征的融合降维，将融合后的特征向量作为SVM分类器的输入，进行模型训练并找出已知状态训练样本中的支持向量，据此确定最优分类超平面；在测试阶段，测取未知状态设备振动信号，将振动信号进行小波包分解，利用PCA进行特征的融合降维，求得用于表征未知状态的特征向量。在训练模型已完成的情况下将用于表征未知状态的特征向量作为SVM分类器的输入，SVM分类器将根据最优分类超平面对用于表征未知状态的特征向量作出分类决策。

4　基于PCA与SVM的滚动轴承故障特征融合分析

4.1试验数据描述

对308轴承分别在外圈滚道剥落、内圈滚道剥落、滚动体剥落和正常4种不同状态下的信号进行分析。测取其振动信号,采样频率为25 kHz,轴承工作转速为1600 r/min,样本长度为8192。构造基于小波包分解的故障特征向量。由于样本数目较多，仅列出外圈滚道剥落故障状态下8个经小波包分解后的结果,见表1,各频带宽为1562.5 Hz,由低到高分布，如频带1的范围为0～1562.5 Hz,频带2的范围为1562.5～3125 Hz,依此类推。经分解可以得到故障的8维特征向量,如外圈剥落故障样本1,e1=(0.086 9240.039 2820.287 580.271 6280.026 9880.035 6710.158 9410.092 986)。

表1　外圈滚道剥落故障信号小波包分解各频带的相对能量比

在试验中共测得试验数据128组,其中滚动体剥落、内圈剥落、外圈剥落以及正常状态各32组。为了方便比较和更好地表现SVM分类器的性能,将原始数据分成训练样本较多和训练样本较少的两组数据集,见表2。

表2　试验样本

4.2基于PCA的轴承故障特征融合分析

将试验数据进一步处理,通过小波包分解提取的8维特征盒图如图2所示。从中可以大致了解8种特征的一些基本情况,如特征5、6比其他特征具有更多的异常点,但其分布的整体变化幅度比其他特征小,变化幅度最大的特征是特征1，特征3、4、7、8整体分布比较均匀。

图2　轴承试验中8种特征数据的描述(已归一化)

将得到的8维特征向量进行基于PCA的融合,提取累积贡献率达到95%的主成分。经过PCA融合后,轴承试验所提取的5个主成分贡献率值见表3,前5个主成分累积贡献率达到95%以上。可以看出主成分1的贡献率最大,达57.8622%,从理论上说主成分1集合了原8维特征57%左右的信息,是所有主成分中最具故障判断价值的成分。

表3　轴承试验所提取的5个主成分贡献率　%

图3为利用PCA方法融合后的前5个主成分特征波形图。可以看出,第1个特征参数主成分1保留了原信号大部分信息,变化趋势较为明显地表征了不同状态下的轴承,与样本状态变化趋势基本保持一致，其他参数的变化整体较为混乱，无规律性可言，对不同状态轴承的表征能力较弱。

图3a为PCA融合后轴承主成分1的特征波形图,4个圆圈分别对应轴承试验中的4种不同状态的轴承,除外圈剥落(样本1～32)与内圈剥落(样本33～64)分辨率较低外，滚动体剥落(样本65～96)与正常状态轴承(样本97～128)间区分度较高。

4.3基于SVM的轴承故障特征分类

4.3.1SVM核函数的选择

(a)主成分1

(b)主成分2

(c)主成分3

(d)主成分4

(e)主成分5图3　轴承试验前5个主成分随样本变化趋势图

为选择合适的核函数以获得SVM最佳的分类性能,分别选择线性核函数、多项式核函数、径向基核函数、双曲正切核函数对样本进行SVM训练。同时为了比较不同SVM分类算法对试验结果的影响，分别选用一对多、一对一算法进行计算。对准确率结果采用5折交叉验证方法进行验证,不同故障类别轴承的分类准确率结果见表4和表5。

表4　不同故障状态的测试分类结果(数据集1)　%

表5　不同故障状态的测试分类结果(数据集2)　%

由表4和表5可知,SVM分类器并没有因为训练样本数据的减少而导致准确率出现大的波动,依然表现出较高的准确率。采用了一对一和一对多两种算法,SVM分类器在准确率方面并没有显著的差距。核函数确定了从样本空间到高维特征空间的非线性映射，不同的核函数及其参数对应着样本数据在高维特征空间分布不同的复杂程度，从而影响最终的分类准确率。因而，选择不同的核函数对分类结果有一定的影响，如双曲正切核函数在本次试验中的分类准确率明显低于其他3种核函数。试验结果显示,径向基核函数的准确率最高，双曲正切核函数最低，线性核函数和多项式核函数的准确率略低于径向基核函数，但明显高于双曲正切核函数，说明在分类准确率上双曲正切核函数综合性能最差，因而选择径向基核函数。

4.3.2基于SVM的轴承故障特征融合

将前文试验中的8维特征向量进行基于PCA的融合,提取累积贡献率达到95%的主成分。将融合后的5个主成分输入SVM分类器进行识别,为避免偶然性，同时用BP神经网络分类器进行结果比较。分类结果见表6。

表6　轴承8维特征PCA融合前后的故障诊断准确率

由表6的结果分析可知,基于PCA和VSM的特征融合无论在诊断的准确率和时间方面都具有优势,准确率可以达到97%以上。因而,将两者相结合能充分利用各特征间的互补性,将特征信息中的冗余信息剔除，最大化压缩信息量，提高特征表征运行状态的能力，从而提高故障诊断率。同时，基于PCA的特征融合方法还能有效降低特征维数，减少分类器的训练时间，这一性能在处理海量数据时具有一定价值。

在轴承试验中,作为SVM分类器输入的5个主成分累积贡献率为97.2840%,这5个主成分几乎包含原有8维特征的全部信息。但在实际运用中,融合前的特征往往较多,为尽可能达到降低维数的要求,应用PCA融合的方法保留主成分贡献率很难达到95%以上，对于故障状态相对不是很复杂的情况,可适当降低主成分贡献率的设定值,如取值在85%左右。在本文中前3个主成分的贡献率为83.5083%,将前3个主成分作为SVM输入进行故障诊断,准确率为82.5641%。相对于取5个主成分，其诊断准确率有较大的下降。

图4为基于PCA的前3个主成分特征绘制的样本空间三维图，可以通过前3个主成分特征表征4种不同状态的轴承。从图4中可以看出，正常状态的轴承最易识别，其分布图也最为集中，其次为外圈剥落，该状态下的分布图也较为紧密，以上两种状态的轴承通过3个主成分特征均能达到很高的识别率。内圈剥落和滚动体剥落这两种状态的轴承较难识别,部分特征间出现了相互干涉的现象,但考虑到这3个主成分累积贡献率仅为83.5083%,且从原8维特征降到3维,特征维数幅度压缩量大使得信息量损失较大，所以出现了部分样本难以区分的情况。因而，为提高诊断的准确率，不应过度对信息进行压缩。

图4　基于PCA融合后前3个主成分的样本分布图

5　结束语

(1)采用PCA和SVM相结合的方法,通过删除冗余特征进行融合的方法可以极大地压缩信息量，既能降低特征维数，降低计算的复杂性,又能有效表征轴承的故障状态，诊断精度也较其他方法高。

(2)对滚动轴承来说，正常状态的轴承较其他状态易识别，外圈剥落次之，内圈剥落和滚动体剥落这两种状态的轴承较接近，相对而言较难识别。因而，为保证故障诊断的有效性，在信息融合过程中不宜过度进行信息的压缩而使信息量损失较大。

致谢感谢加拿大阿尔伯特大学可靠性实验室提供的技术和条件支持。

[1]徐晓滨,王玉成,文成林.评估诊断证据可靠性的信息融合故障诊断方法[J].控制理论与应用,2011,28(4):504-510.

Xu Xiaobin,Wang Yucheng,Wen Chenglin.Information-fusion Method for Fault Diagnosis Based on Reliability Evaluation of Evidence[J].Control Theory & Applications,2011,28(4):504-510.

[2]王赟松,褚福磊, 何永勇, 等. 基于信息融合技术的发动机故障诊断的研究[J].内燃机学报,2003,21(5):374-378.

Wang Yunsong,Chu Fulei,He Yongyong,et al.Study on Fault Diagnosis for Automobile Electronically Controlled Engine Based on Data Fusion Technique[J].Transactions of CSICE,2003,21(5):374-378.

[3]Otman B,Yuan X H.Engine Fault Diagnosis Based on Multi-sensor Information Fusion Using Dempster-Shafer Evidence Theory[J].Information Fusion,2007,8(4):379-386.

[4]Niu G,Yang B S.Intelligent Condition Monitoring and Prognostics System Based on Data-fusion Strategy[J].Expert Systems with Applications,2010,37(12):8831-8840.

[5]Peng H,Long F,Ding C.Feature Selection Based on Mutual Information:Criteria of Max-dependency,Max-relevance,and Min-redundancy[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(8):1226-1238.

[6]李冰,张培林,任国全,等.基于互信息的滚动轴承故障特征选择方法[J].测试技术学报,2009,23(2):183-188.

Li Bing,Zhang Peilin,Ren Guoquan,et al.Features Selection for Rolling Bearing Fault Diagnosis Based on Mutual Information[J].Journal of Test and Measurement Technology,2009,23(2):183-188.

[7]Zhao Xiaomin.Data-driven Fault Detection,Isolation and Identification of Rotating Machinery:with Applications to Pumps and Gearboxes[D].Edmonton:University of Alberta,2012.

[8]蒋玲莉,刘义伦,李学军,等.基于SVM与多振动信息融合的齿轮故障诊断[J].中南大学学报(自然科学版),2010,41(6):2184-2188.

Jiang Lingli,Liu Yilun,Li Xuejun,et al.Gear Fault Diagnosis Based on SVM and Multi-sensor Information Fusion[J].Journal of Central South University(Science and Technology),2010,41(6):2184-2188.

[9]周荣义,钟岸,任竞舟,等.基于主成分分析和神经网络的事故预测方法及应用[J].中国安全科学学报,2013,23(7):55-60.

Zhou Rongyi,Zhong An,Ren Jingzhou,et al.An Accident Forecasting Method of ANN Based on PCA and Its Application[J].China Safety Science Journal,2013,23(7):55-60.

[10]Jolliffe I T.Principal Component Analysis[M].New York:Springer-Verlag,2002.

[11]丁世飞,齐丙娟,谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报,2011,40(1):2-10.

Ding Shifei,Qi Bingjuan,Tan Hongyan.An Overview on Theory and Algorithm of Support Vector Machines[J].Journal of University of Electronic Science and Technology of China,2011,40(1):2-10.

[12]聂磊,黄圣国,舒平,等.基于支持向量机(SVM)的民用飞机重着陆智能诊断研究[J].中国安全科学学报,2009,19(7):149-154.

Nie Lei,Huang Shengguo,Shu Ping,et al.Intelligent Diagnosis for Hard Landing of Aircraft Based on SVM[J].China Safety Science Journal,2009,19(7):149-154.

[13]程军圣,于德介,邓乾旺,等.连续小波变换在滚动轴承故障诊断中的应用[J].中国机械工程,2003,14(23):2037-3040.

Cheng Junsheng,Yu Dejie,Deng Qianwang,et al.An Application of Continuous Wavelet Transform to Fault Diagnosis of Rolling Element Bearings[J].China Mechanical Engineering,2003,14(23):2037-3040.

(编辑陈勇)

Rolling Bearing Fault Feature Fusion Based on PCA and SVM

Gu YingkuiCheng ZixinZhu Fanlong

Jiangxi University of Science and Technology,Ganzhou,Jiangxi,341000

To effectively reduce the dimension of rolling bearing fault features and improve the accuracy of diagnosis,the PCA and SVM were applied in the fusion of bearing fault features,and the corresponding decision-making process was presented.By using the fault feature extraction algorithm and eigenvector constructing methods which were proposed based on wavelet packet decomposition,the bearing vibration signals in different states were decomposed to get the 8-dimensional feature sets which could be used to characterize the running conditions of the bearing.The cumulative contribution rate of 95% principal components were extracted by using PCA method and were input into SVM classifier for identification.Results show that the fault feature dimensions of rolling bearing can be reduced from 8-dimensions to 5-dimensions,which can still characterize the bearing status effectively,and the computational complexity can be reduced.The fault diagnosis accuracy is higher than 97%,and the diagnosis time is short relatively.The identification accuracy of four bearing status from high to low in turn is normal, outer ring peel, roller peel and inner ring peel.It can ensure the safe operation of the equipment and provide theoretical basis for fast fault diagnosis.

principal component analysis(PCA);support vector machine(SVM);feature fusion;fault diagnosis;rolling bearing

2015-01-14

国家自然科学基金资助项目(61164009, 61463021); 江西省自然科学基金资助项目(20132BAB206026);江西省教育厅科学技术研究项目 (GJJ14420); 江西省青年科学家培养对象计划资助项目(20144BCB23037)

X928.03; TH165.3DOI：10.3969/j.issn.1004-132X.2015.20.014

古莹奎,男,1976年生。江西理工大学机电工程学院教授、博士。主要研究方向为机械装备可靠性与健康管理。发表论文40余篇。承姿辛,女,1991年生。江西理工大学机电工程学院硕士研究生。朱繁泷,男,1989年生。江西理工大学机电工程学院硕士研究生。