基于Lanczos法的模态重分析法在拓扑优化中的应用

刘　丹　王　琥

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

基于Lanczos法的模态重分析法在拓扑优化中的应用

刘丹王琥

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

在拓扑优化中,经常要求对结构进行修改,快速准确地计算修改后结构的低阶特征值对于提高整个结构优化的效率非常重要。将基于Lanczos算法的模态重分析法应用于拓扑优化过程中,利用初始结构模态分析结果,结合Lanczos算法和投影技术,采用缩减基方法求解修改结构的固有频率和振型, 则该方法同时具备了Lanczos向量快速收敛的优点和基于全局近似的缩减基向量的高精度。刚架算例验证了该重分析法的高精度。固支方形板和车架结构优化结果表明,该方法在保证求解精度的同时能够在一定程度上提高优化迭代速度。

Lanczos算法;模态重分析;拓扑优化;频率优化

0　引言

在拓扑优化中,随着结构的不断修改,需要求解一系列形如KiX=P的大规模线性方程组,其中Ki是在结构拓扑优化中第i步结构刚度阵,X是待求结构的响应,P是载荷向量。在结构拓扑优化中求解一系列大规模线性方程组已成为计算速度的瓶颈。结构重分析技术就是利用初始结构响应,设计高效重分析算法来求解修改后结构的新响应而不对新结构进行完整分析的技术，可以显著降低计算成本,从而加速优化过程。而修改结构的模态分析比静力分析更加耗时,所以模态重分析就显得更加重要。

近年来,很多学者研究了结合直接法和近似法形成改善的动力学重分析方法的途径,如黄海等[1]将摄动和Padé逼近法、迭代和组合逼近相结合形成动力学重分析方法。这些方法可用于结构形状修改和拓扑修改(包括自由度增加)的动力学重分析。但到目前为止,还没有真正形成一些十分简便、快速、高效和通用的拓扑修改动力学重分析方法。Kirsch[2]将静力学组合近似法引入结构振动分析过程,将模态方程和静力平衡方程进行了等效处理,在Krylov子空间内构造缩减基,求解降阶的模态方程,并给出了误差评估[3]。同样,组合近似法对于结构小修的计算效果较好，但是结构修改量增大或需要计算高阶模态时，常常会出现较大的误差。为了提高组合近似法在结构大修改时的求解精度,文献[4-6]提出了扩展的组合近似法,利用瑞利商提高了组合近似法的求解精度,但却增加了计算量。Huang等[7]提出了基于扩展基向量和瑞利-里兹分析的模态重分析方法。

结构的频率在许多工程领域都是关注的重点。工程结构在动载荷作用下的动响应在很大程度上依赖于结构前几阶固有频率。当动载荷频率接近于被作用结构的固有频率之一时，该结构会出现过度振动。为了避免严重振动，常常需要调整结构基频或前几阶频率，使之远离动载荷频率范围。因此，频率优化是结构拓扑优化中很重要的一部分。本文采用双向渐进优化方法(evolutionary structural optimization,BESO)解决频率优化问题,该方法是在一定体积约束条件下，最大化第一阶固有频率。逐渐删除材料的双向渐进结构优化概念在频率优化中已得到推广和有效应用。优化过程中求解特征值问题时应用基于Lanczos算法的模态重分析法可以在保证精度的同时，在一定程度上提高求解效率。

1　模态重分析

考虑初始无阻尼系统特征值问题：

K0Φ0=Λ0M0Φ0

(1)

其中,K0和M0分别为初始结构刚度矩阵和质量矩阵,Λ0和Φ0分别为初始结构的特征值矩阵和相应的模态向量组,结构发生修改时,修改后系统的特征值问题可以表示为

KmΦm=ΛmMmΦm

(2)

(3)

(4)

下标n表示初始结构的自由度,m表示修改结构新增加的自由度。Λm和Φm为修改后结构的特征值矩阵和相应的模态向量组。直接求解式(2)可以得到精确解,但是为提高效率,我们可以利用初始分析的结果近似求解结构修改之后的方程。文献[7]提出基于扩展基向量和瑞利-里兹分析的模态重分析方法，主要步骤如下。

(1)假设Φm和Λm的近似表达为

(5)

Λm≈Λ0

(6)

(2)把式(3)～式(6)代入式(2),展开可得

(ΔKmn-λ0iΔMmn)φ0i=-(ΔKmm-λ0iΔMmm)Δφi

(7)

所以有

Δφi=-(ΔKmm-λ0iΔMmm)-1·

(ΔKmn-λ0iΔMmn)φ0i

(8)

(3)三角分解刚度矩阵Km为

Km=LDLT

(9)

(4)求解静态方程,获得改善的里兹基向量:

(10)

(5)构造缩减方程:

(11)

(12)

(6)最终的近似特征值和特征向量分别为

(13)

(14)

在此基础上，改进的单步摄动瑞利商逆迭代法[8]将单步摄动法和瑞利商逆迭代法结合起来,获得了更好的效果。

2　基于Lanczos算法的模态重分析法

本文提供了一种将Lanczos算法、投影技术和缩减基法相结合的模态重分析方法。同主流重分析方法相比，本方法并没有直接采用初始特征向量构造缩减基向量组,而是基于Lanczos向量良好的正交性和快速收敛性[9],利用Lanczos法迭代出前几阶Lanczos向量做基向量。主要步骤如下。

(1)计算修改结构的刚度矩阵K和质量矩阵M。

(2)对刚度矩阵K进行三角分解。

(3)选取初始分析所得特征向量Φ0为初始基向量构造Lanczos向量：

(15)

q0是初始结构的特征向量,正交化得

(16)

(17)

正则化得

(18)

qi即为迭代出的Lanczos向量。这就将广义特征值问题KΦ=ΛMΦ转换为Lanczos向量空间内对角矩阵Tm的标准特征值问题，即求解

TmZ=Z λ

(19)

λ=diag(λi)Λ=λ-1

(4)构造投影向量矩阵T。

(5)计算缩减矩阵KR和MR：

(20)

(6)求解特征值方程KRy=λMRy,得到前几阶固有频率,再用线性组合法计算出相应的主振型。

2.1截断的Lanczos向量

选取已求得初始结构的特征向量作为初始基向量，利用Lanczos算法迭代出前几阶向量。求解过程中，只需要采用PARDISO程序包一次三角分解稀疏矩阵K,之后就是前后回代计算。设v0是要求解的修改结构的特征向量,r0是初始结构求得的特征向量,令

(21)

则

(22)

迭代出基向量：

(23)

将式(22)代入式(23)得

(24)

正交化得

(25)

将式(20)和(23)代入式(24),正交化结果为

(26)

最后可简化得

r1=H·Δv+ΔvTpv0

(27)

因此

|r1|≤|H||Δv|+|p||v0||Δv|=

(|H|+|p||v0|)|Δv|=c|Δv|

其中,c为一定常数。

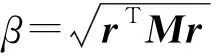
2.2投影方法

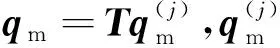
(28)

(29)

设n是Lanczos向量截断阶次,投影基矩阵的大小为nsdof×(n+1)j,如此缩减矩阵之后，需要求解的特征值矩阵规模就减小为(n+1)j×(n+1)j,大大缩短了CPU的运算时间。

3　频率优化

动力问题设计中,通常需要将结构的基频或低频控制在一定范围内以避免共振,BESO在处理频率优化时简单有效。与刚度优化类似，频率优化也要根据灵敏度来确定需要删除的单元。

3.1拓扑优化问题

为了辨识结构修改的最好位置，经常需要进行灵敏度分析。在有限元分析中，结构动特性一般特征值问题为

(30)

式中，ωi为第i阶固有频率；φi为对应于ωi的特征矢量。

固有频率及相应的特征矢量通过瑞利商相互关联:

(31)

其中,模态刚度ki和模态质量mi分别定义为

这里考虑拓扑优化，最大化一阶固有频率，优化问题表示如下：

(32)

式中,Vi为单个单元的体积;V*为预先设定的结构体积;N为结构中总的单元数目。

3.2材料插值方法

为了获得设计变量的梯度信息,我们将材料在xmin和1之间进行插值。假设原始的材料弹性模量和密度分别为E0和ρ0,则有：

(33)

式中,p为惩罚系数。

为了避免当xi=xmin时,由于对刚度和质量的惩罚比值太大而引起局部奇异模态[10],因此,我们将材料插值表示为

(34)

根据式(31),可以求得目标函数ω1的灵敏度为

(35)

根据式(31)以及特征向量关于质量矩阵正交的性质,可以将式(35)简化为

(36)

3.3拓扑优化的进化过程

采用双向渐进结构优化方法，逐渐从结构中删除材料,使结构频率能移向期望值。在优化迭代过程的每一步，已经算得当前结构的固有频率与主振型，并确定出可删除单元集合。可删除单元是当前结构的一部分，利用已知的主振型即可对删除某个单元所引起的特征值改变量进行估计。本文的模态重分析方法可以加快优化迭代速度,主要步骤如下：

(1)用有限元精细网格离散结构；

(2)确定BESO方法的参数，如目标体积V*、进化率er和惩罚值p；

(3)采用有限元Lanczos方法求解特征值问题；

(4)用式(36)计算每个单元的灵敏度,通过平均单元过滤器内的单元灵敏度和平均单元历史灵敏度来更新单元灵敏度，并删除一定数量具有最小灵敏度的单元；

(5)采用本文基于Lanczos算法的模态重分析方法近似求解修改结构的特征值；

(6)在结构体积约束条件限制下,重复步骤(3)～步骤(5)直至达到最佳结构需求。

4　数值算例

为了验证该方法的有效性，本文给出三个数值算例，第一个算例验证该重分析方法的精确性，后两个算例验证该方法在结构拓扑优化过程中的应用可行性。

4.1刚架结构

如图1a所示的平面刚架结构，刚架的材料参数为：E=2.1×1011Pa,ρ=7800 kg/m3,梁单元的横截面半径r=0.02 m,节点1到2之间的长度是0.5 m,节点1到3之间的长度也是0.5 m,节点1和节点2固定。假设结构拓扑修改之后增加了2个节点和3个梁单元，如图1b所示。同时刚架的材料参数变化为E=1.8×1011Pa,质量密度变为ρ=6800 kg/m3,节点1到2和节点1到3的长度都变为0.625 m。

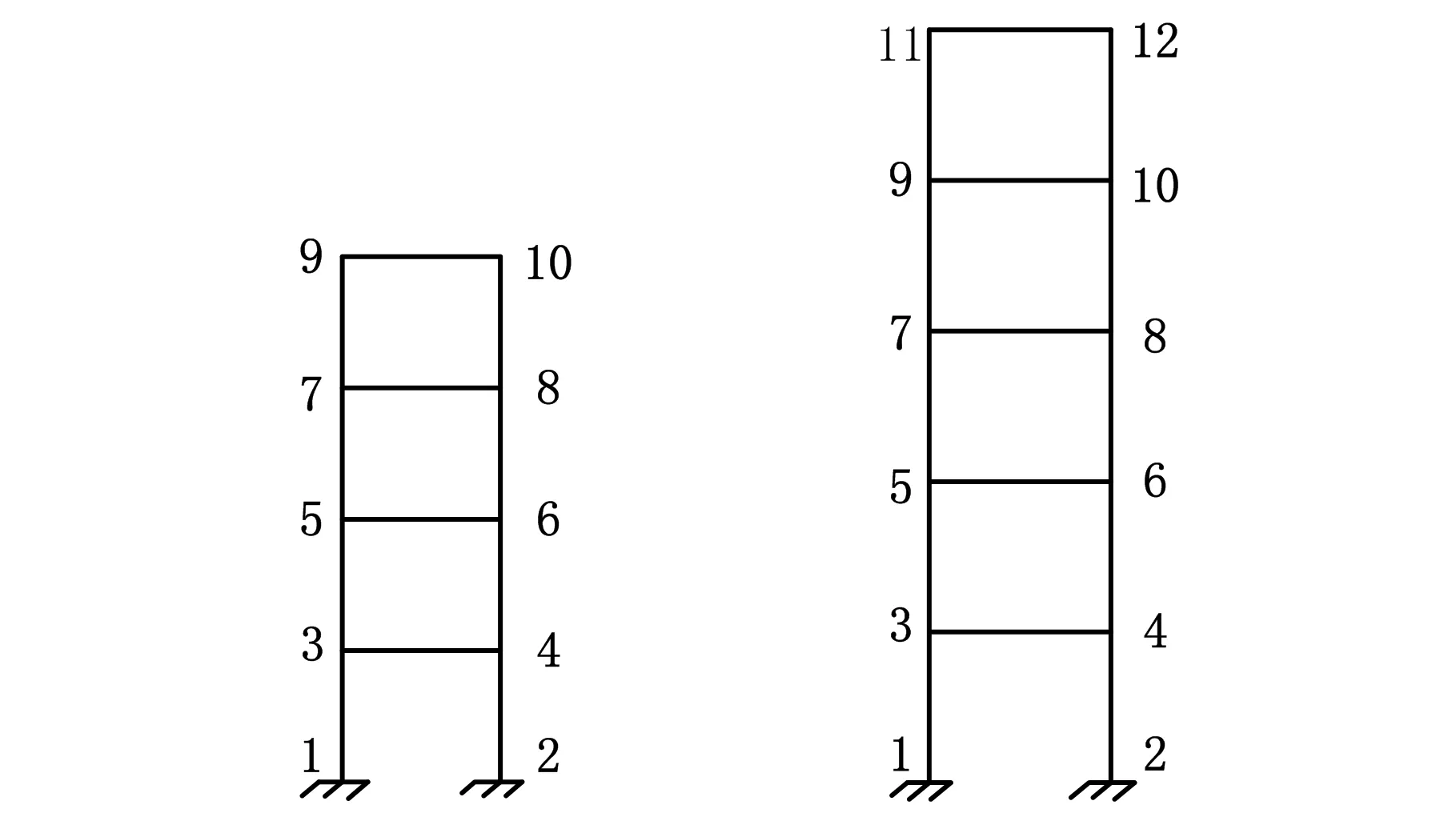
(a)刚架初始结构(b)刚架修改后结构图1　刚架结构拓扑修改

以λi表示拓扑修改后有限元计算参考解,λi0表示近似方法求得的解,下标i表示第i阶特征值。相对误差定义为

从表1可以看出，本文方法求得前6阶特征值近似值与有限元计算参考解是一致的，相对于其他方法，精度有一定提高。

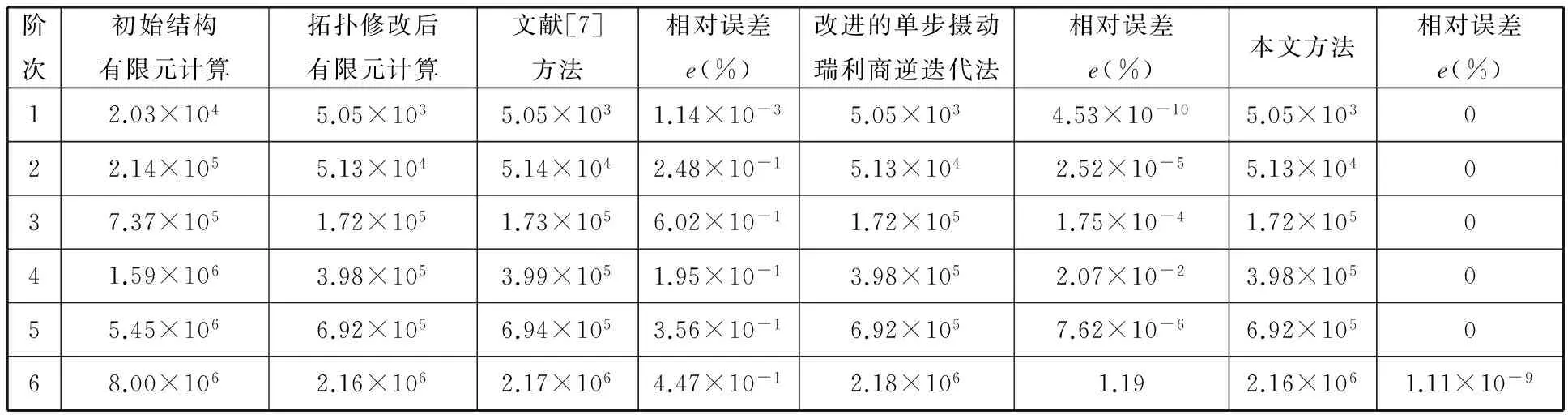
表1　刚架结构拓扑修改前后前6阶特征值比较

4.2固支方形板

边长为20 m的正方形板，厚度为1 m，四边固支。在ANSYS中细分模型为40×40的四边形壳单元网格。材料参数如下：弹性模量E=100 GPa，泊松比υ=0.3,密度ρ=7800 kg/m3,在板中心施加集中非结构质量m=3.12×105kg。BESO参数为：进化率er=2%,最大增加率RA,max=2%，单元过滤半径rmin=1.5 m,惩罚因子p=3.0,xmin=10-6,体积约束为初始体积的50%。

最终的拓扑优化结果如图2所示。

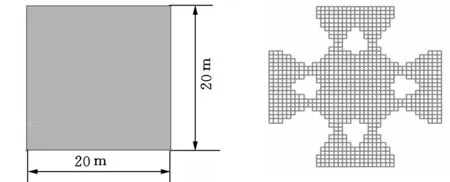
(a)固支方板初始设计域(b)固支方板拓扑优化后模型图2　固支方板

图3显示了基频和体积分数的迭代历史进程，最初基频随着体积的减小呈缓慢下降趋势，在达到体积约束后，基频逐渐收敛到一定值。其中ω1表示全分析求得的一阶角频率，ω2表示本文重分析方法求得的一阶角频率，可以看出两者结果十分相近。

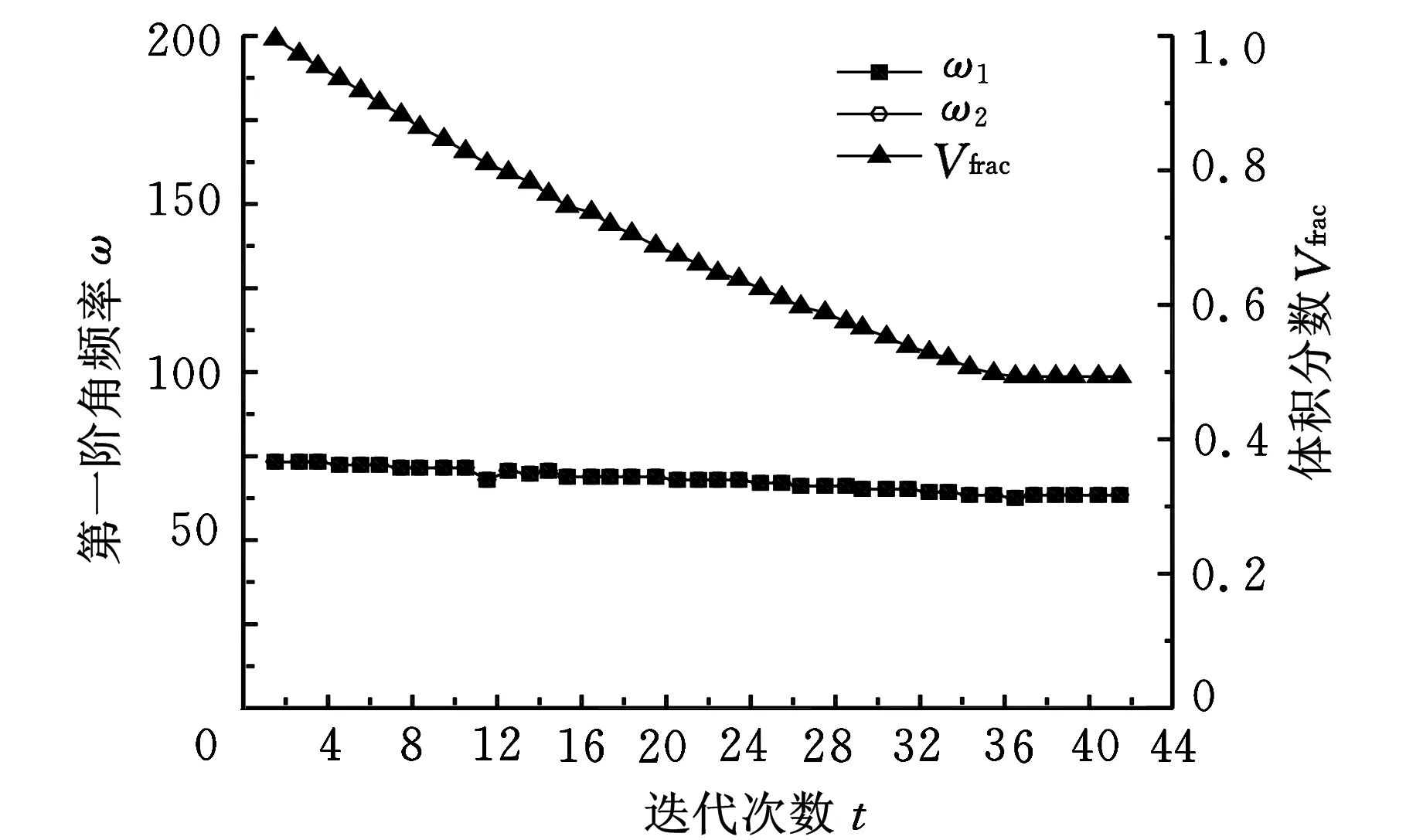
图3　一阶角频率随迭代次数变化曲线

优化过程中，每近似分析十步进行一次全分析，保证了解的正确性。

4.3车架结构

轻型载货汽车车架设计的初始模型如图4所示，本算例是优化车架横梁的位置，车架的基本参数为：E=200 GPa,ρ=7800 kg/m3,μ=0.3。

图4　车架设计初始模型

BESO参数为：er=2%,RA,max=2%，Rmin=75 mm,p=3.0,xmin=10-2，优化区域为车架横梁,设置纵梁为非优化区域。优化目标为maxωi;约束条件为V*≥30%Vo。

优化迭代历史次数与一阶角频率和体积分数的关系曲线如图5所示。

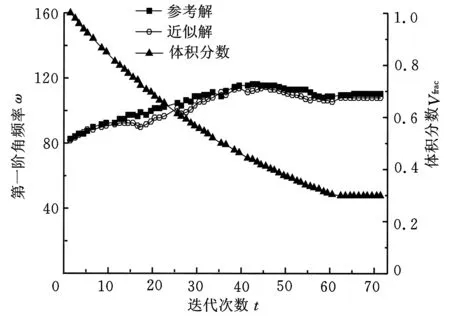
图5　一阶角频率参考解和近似解随迭代次数变化曲线

最后拓扑优化后的车架结构如图6所示，符合实体货车车架的基本构造，横梁一般都布置在车架前部和后部以承收货车大部分载荷。

图6　车架拓扑优化后模型

为保证特征解的收敛，优化过程中，每近似分析五步就进行一次全分析。由于每次最多只删除总体积的2%，经过60步迭代后，体积减小到原优化区域体积的30%，在之后的几步迭代中目标值逐渐趋于稳定。迭代停止的条件为

其中，k是当前迭代步数；τ是允许的收敛误差；N是一整数，本算例中取5，表示最后的10步迭代，特征值的改变量已经足够小。

从图5中可以看出,采用本文方法优化固有频率所得近似解和参考解十分接近，一阶固有角频率从82.96 rad/s增加到110.36 rad/s,增加33%。同时，求解时间从1946 s缩短到1494 s,相较于全分析缩短了23%,保证求解精度的同时提高了求解效率。

5　结论

本文将Lanczos算法和缩减基法相结合,提出了一种高精度的模态重分析方法。该方法在结构拓扑优化中得到很好应用，可以在保证求解精度的同时有效节省求解时间。

[1]黄海,陈塑寰,孟光.摄动法结合Padé逼近在结构拓扑重分析中的应用[J]. 应用力学学报,2005，22(2)： 155-158.

Huang Hai,Chen Suhuan,Meng Guang.The Application of Perturbation Method Combined with Padé Approximation in the Structural Topology Reanalysis[J].Chinese Journal of Applied Mechanics,2005,22(2):155-158.

[2]Kirsch U.Approximate Vibration Reanalysis of Structures[J].AIAA Journal,2003,41(3)：504-511.

[3]Kirsch U,Bogomolni M.Error Evaluation in Approximate Reanalysis of Structures[J].Structural and Multidisciplinary Optimization,2004,28(2/3):77-86.

[4]吕振华.结构动力学修改重分析方法的发展[J].计算结构力学及其应用,1994,11(1):85-91.

Lü Zhenhua.Development of Reanalysis Method for Structural Dynamics Modifications[J].Computional Structural Mechanics and Application,1994,11(1):85-91. [5]Chen Suhuan, Yang Xiaowei. Extended Kirsch Combined Method for Eigenvalue Reanalysis[J].AIAA Journal, 2000, 38(5): 927-930.[6]Feng Rong, Chen Suhuan, Chen Yudong. Structural Modal Reanalysis for Topological Modifications with Extended Kirsch Method[J]. Computer Methods in Applied Mechanics and Engineering，2003,192(5):697-707.

[7]Huang Cheng，Chen Suhuan，Liu Zhongsheng. Structural Modal Reanalysis for Topological Modifications of Finite Element Systems[J]. Engineering Structures，2000，22：304-310.

[8]何建军. 结构拓扑修改动力学重分析方法的研究[D]. 西安：西北工业大学，2006.

[9]王欣欣. 求解对称矩阵特征值问题的Lanczos算法的改进及分析[D]. 哈尔滨：哈尔滨工业大学，2008.

[10]Huang Xiaodong,Zuo Zhihao,Xie Yimin.Evolutionary Topological Optimization of Vibrating Continuum Structures for Natural Frequencies[J]. Computers and Structures, 2010，88(5):357-364.

(编辑袁兴玲)

Application of Lanczos-based Modal Reanalysis Algorithm in Topological Optimization

Liu DanWang Hu

State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University,Changsha,410082

In topological optimization,the structures were often required to make some modifications,and it was very important for improving the effciency of optimization that the low-order eigenvalues could be calculated accurately and quickly.The Lanczos-based modal reanalysis method was applied to topological modification.The presented method which combined Lanczos algorithm and projection techniques,solved the natural frequency and mode shapes for the modified structures utilizing the already obtained eigenvectors with reduced-basis algorithm.The major advantages laid that the fast convergence of Lanczos vector and high-accuracy of reduced-basis method based on global approximations.A stiff frame example was demonstrated the high accuracy of the reanalysis method.The optimization results of the clamped square plate and vehicle frame indicate that the method can also ensure the calculation accuracy and optimization iteration speed to a certain extent.

Lanczos algorithm;modal reanalysis;topological optimization;frequency optimization

2014-01-21

国家自然科学基金资助项目(11172097)；教育部新世纪优秀人才支持计划资助项目(NCET-11-0131);湖南省自然科学基金资助项目(11JJA001)

TH11;O32DOI：10.3969/j.issn.1004-132X.2015.11.015

刘丹,女,1987年生。湖南大学机械与运载工程学院硕士研究生。研究方向为模态重分析及结构优化。王琥，男，1975年生。湖南大学机械与运载工程学院副教授。