不确定需求下的设备动态布局方法
2015-10-29马淑梅蔡惠森张一帆李爱平
马淑梅 蔡惠森 张一帆 李爱平
同济大学,上海,201804
不确定需求下的设备动态布局方法
马淑梅蔡惠森张一帆李爱平
同济大学,上海,201804
针对现有车间设备动态布局方法存在的不足,在考虑产品需求不确定性对布局性能稳定性影响的基础上,提出了一种结合模糊理论与改进遗传算法的不等面积设备动态布局方法。分析了产品需求不确定性及其随时间变化特性,引入了三角模糊数描述不确定产品需求;通过分析各生产阶段间的设备重组过程,将动态布局转化为数个静态布局,构建了基于柔性区域结构的不确定需求动态布局模型。结合三角模糊数运算及排序方法与自适应局部搜索机制提出了改进遗传算法,以物料搬运及设备重组费用总和为优化目标,解决不确定需求下的不等面积设备动态布局问题。通过算例测试和实例分析,验证了所提方法的有效性和实用性。
不确定需求;改进遗传算法;不等面积;设备动态布局
0 引言
车间设备布局规划是制造过程的重要环节,良好的车间布局可以提高企业整体效益,降低高达50%的生产运营费用[1]。传统静态布局方法假设设备间物流量固定不变,忽视了品种、产量等因素波动的长远影响。动态车间设备布局方法将整个布局使用期限划分为多个生产阶段,综合考虑各个生产阶段的产品类型及需求信息,并在生产阶段间进行设备重组,因其对市场变化的快速响应能力而引起学者们的广泛关注[2-4]。在设备动态布局规划中,影响布局性能的主要因素有规划中所使用信息的准确性、设备布局模型和求解算法。
大多数动态布局研究均假设规划中使用的信息是绝对准确的,但是布局规划必须在产品投产前完成,规划中涉及的品种、需求等与产品相关的信息均由市场预测方法获得,具有不确定性。再者,由于长期预测比短期预测准确性更低,信息的不确定性随着时间推移而增大,故对布局性能的影响也随之增大。在布局规划涉及的诸多信息中,需求信息直接影响设备间物流量的大小,对布局性能稳定性影响最为严重。
近年来,开始有学者在动态布局规划中,考虑需求不确定性的影响。Balakrishnan等[5]研究了动态布局中产品需求的预测误差问题,证明了产品需求的不确定性对布局性能稳定性影响极大。Samarghandi等[6]采用模糊理论对不确定的物流量进行建模,研究车间设备动态布局问题,但是没有考虑不确定性随时间增大的性质。Drira等[7]研究了不确定需求下的动态布局问题并提出了一种有效的求解方法。以上研究均说明了考虑需求的不确定性可以提升布局面对需求波动时性能的稳定性,但是在布局模型上均采用离散式模型,假设所有设备形状尺寸均相同,在生产实际中,易造成空间浪费,最终获得的离散式块状布局亦不利于转化为生产实际应用。
设备布局模型可以分为离散式和连续式,相比离散式布局模型,连续式布局模型考虑设备面积不尽相等的影响,以期获得更贴合实际的设备布局方案。由于求解相对困难,连续式布局模型主要被应用于静态布局的研究中,在动态布局中的应用较少。McKendall等[8]解决了基于混合整数规划的动态布局问题;Mazinani等[9]则研究了以柔性区域结构为布局模型的动态布局问题,但是均未考虑需求的不确定性。由于解决组合优化问题的良好表现以及易于编码等优点,遗传算法被广泛地应用于设备动态布局问题中[10]。遗传算法在解决较小规模问题时表现优异,但是在较大规模问题求解过程中也面临着收敛速度缓慢和陷入局部收敛等问题。动态布局具有多阶段多约束特性,属于大规模问题,因此应用遗传算法求解动态布局问题时通常需对算法进行改进。
综合以上分析可知,在不确定需求环境下的动态布局问题研究中,还存在有待深入研究的地方。在需求信息的处理上,需要考虑需求不确定性对布局性能稳定性的影响,所以必须正确描述需求不确定性及其随时间增大的特性;在布局模型上,为更贴合实际并提高车间面积利用率,必须考虑设备面积不尽相等的实际情况,从而使布局方案在转化为生产应用时更为容易;在求解算法上,解决较大规模问题时,算法应具有较快的收敛速度,并能有效避免局部收敛。
因此,本文采用模糊理论描述产品需求不确定性以提升布局面对需求波动时的性能稳定性,同时避开概率分布函数所引起的计算复杂性,构建以针对不等面积设备的多行线性布局模型为基础的动态布局模型;引入自适应局部搜索机制来改进遗传算法性能,在增加较小运算量的前提下提升遗传算法的收敛速度并强化搜索方向性;再将改进遗传算法与三角模糊数运算与排序方法结合,解决不确定需求下的动态布局问题。
1 不确定需求下的不等面积设备动态布局模型
1.1不确定需求的处理方法
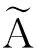
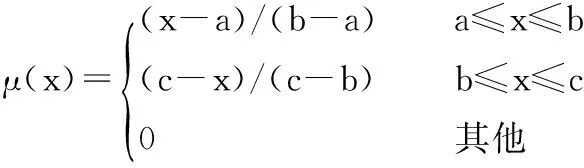
(1)
由隶属函数可以看出,b为可能性最大的值,而上限c与下限a之差的大小则表示该三角模糊数不确定性的大小。
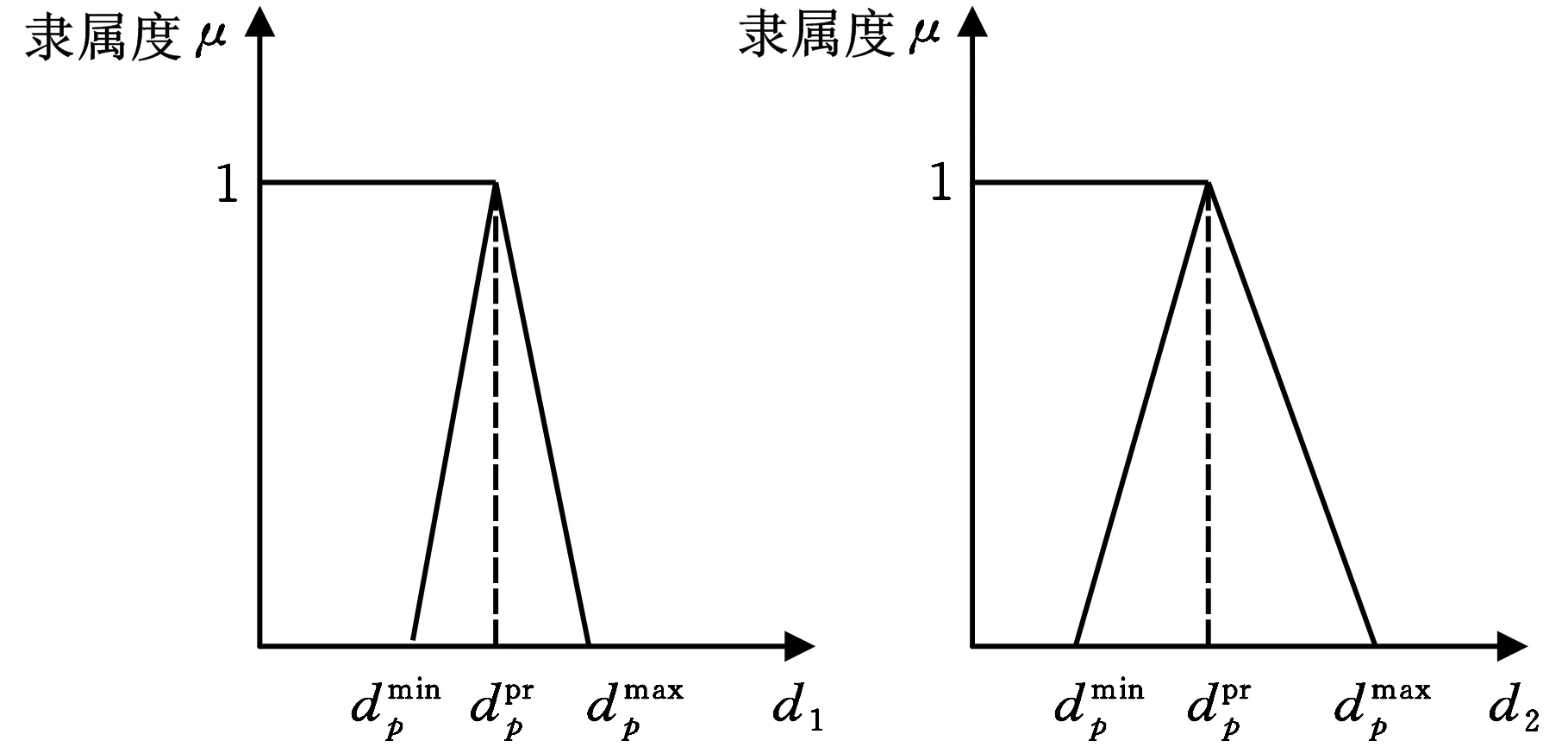
(a)生产阶段1(b)生产阶段2
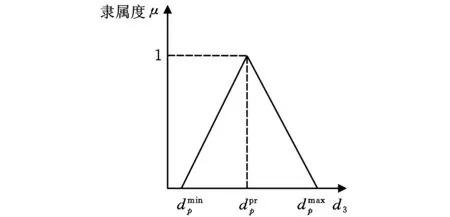
(c)生产阶段3图1 不同生产阶段的需求不确定性
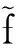
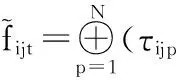
(2)
式中,N为产品种类数。
1.2问题描述与相关假设
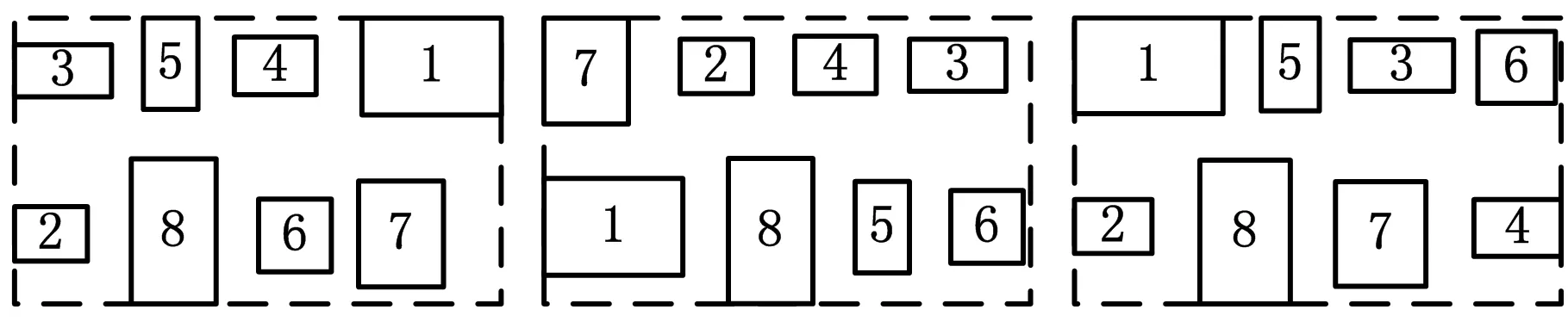
在多品种加工车间中,将车间布局的规划使用期限划分为多个生产阶段,每个产品在每个阶段的具体产量需求数据通过预测获得,具有不确定性;因为长期预测的可靠性比短期预测的可靠性低,所以产品需求数据的不确定性随生产阶段的推移而增大。本文研究的问题就是在考虑上述产品需求不确定性的前提下,在每个阶段对已知的M台不等面积设备进行布局,并允许阶段间设备重组,以物料搬运与设备重组费用总和最小为目标,最终获得切合实际的动态布局方案。
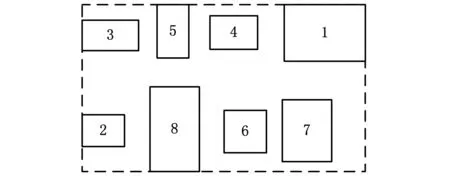
连续型布局模型主要有混合整数规划(mixed-integer programming, MIP)和柔性区域结构(flexible bays structure, FBS)两类。混合整数规划虽然理论上可以获得物料搬运费用更小的布局方案,但是由于过多的边界参数导致求解困难。相比混合整数规划模型,柔性区域结构求解更为简单,也是最容易转化为实际应用的布局模型[11]。多行线性布局[12]是柔性区域结构的特殊形式,其每一行相当于柔性区域结构中的一个区域,并且增加了设备间距和行间距约束,因此具有易于转化为实际应用、求解相对容易的优点,是一种面向不等面积设备的设备布局模型。本文采用多行线性设备布局模型,并假设:①布局车间和设备形状均为矩形且尺寸已知;②设备放置的方向确定;③布局车间生产产品型号及其对应的单位物流量已知。
图2是多行线性车间示意图,M台设备分行布置,在同一行内各设备纵向(y轴)坐标相同,L、W分别为车间的长度和宽度。xit、yit为设备i几何中心在t阶段时的x、y坐标,hij为设备i与j间要求的横向最小距离;s0为最小纵向行间距;so x、soy为设备边界与车间边界的横向安全距离和纵向安全距离;six、siy分别为设备i的横向和纵向尺寸。具体约束条件表达如下。
(1)设备间横向距离约束。即在水平方向相邻设备的距离必须不小于设备间要求的横向最小距离hij:

(3)
式中,Zikt为决策变量,如果在t阶段设备i布置于k行则取1,否则取0。

图2 多行线性设备布局示意图
(2)设备行间距约束。即任意两行设备(p行、q行)的行间距必须不小于纵向行间距要求s0:
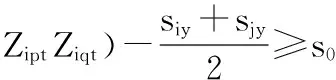
(4)
(3)边界约束。为便于物料搬运和人员运动,设备边缘与车间边界间的距离必须不小于最小安全距离:
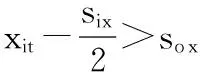
(5)
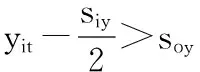
(6)
设备重组是在已有布局上进行设备位置改变的复杂过程。本文根据车间实际情况,简化设备重组过程,假设在车间边缘位置有足够大的设备暂存区,则相邻生产阶段间的设备重组步骤如下:
(1)在待重组设备中随机选择一台设备Mn为当前重组设备,先将该设备Mn目标位置上的现有设备移至暂存区,再将设备Mn移至目标位置;
(2)在暂存区设备中选择一台设备为当前重组设备,按照步骤(1)的方法对当前重组设备进行位置重组,重复此步骤直至暂存区上无设备存放;
(3)判断是否完成所有设备重组,若未完成,返回步骤(1)。
图3所示为设备Mn的重组过程,先将Mn目标位置上的设备Mk、Mj移至暂存区,再将设备Mn移至目标位置。
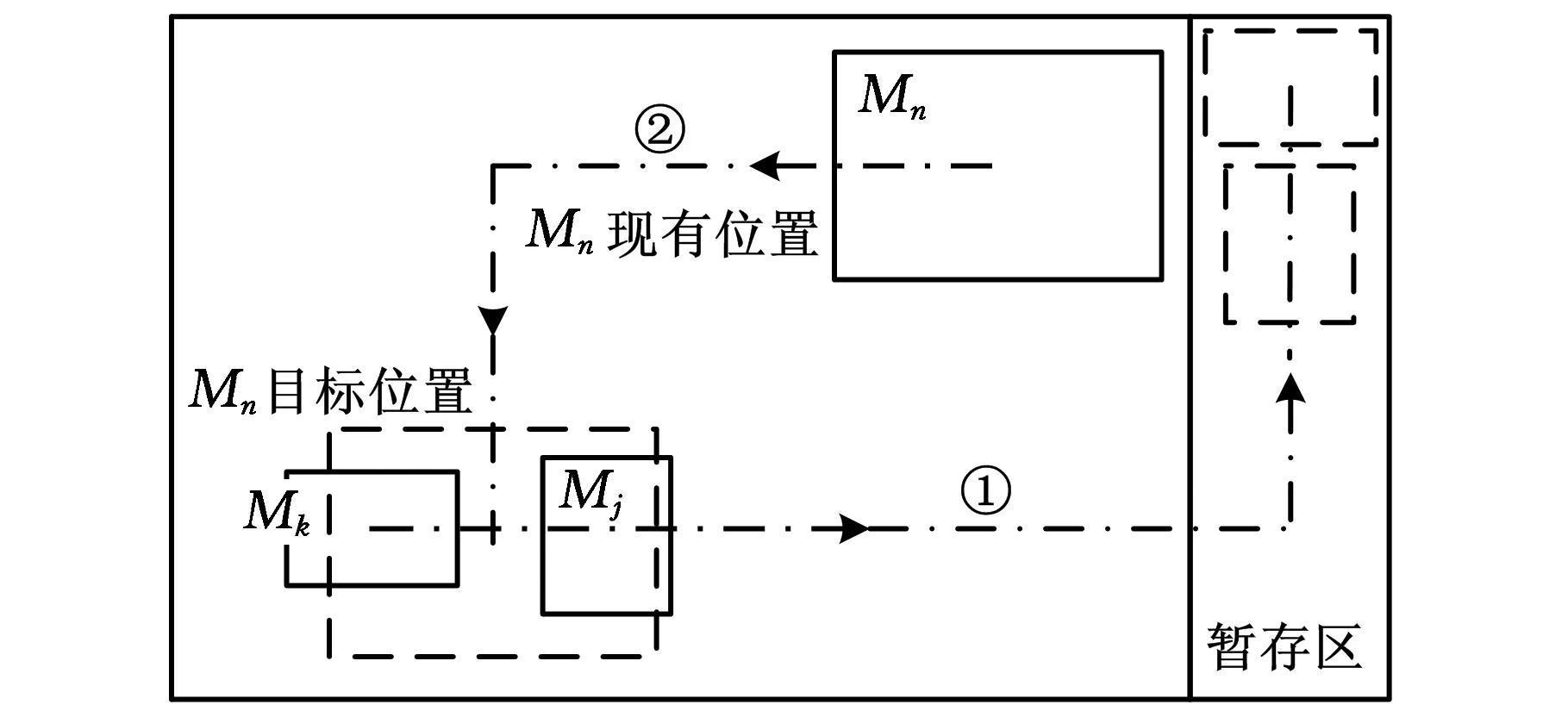
图3 动态布局重组过程
1.3优化目标模型
车间设备布局的主要优化目标是物料搬运费用最小,因此求解时必须考虑布局重组产生的费用。按照上述动态布局设备重组过程,阶段间的设备重组费用主要由设备从现有位置移至目标位置、设备从现有位置移至暂存区和设备从暂存区移至目标位置三个设备移动动作所产生。车间动态设备布局方法的优化目标为整个规划期物料搬运与设备重组费用总和最小,即
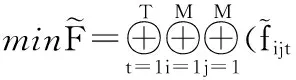
(7)
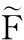
2 基于改进遗传算法的设备动态布局问题求解方法
2.1遗传算法的改进
本文选择遗传算法作为求解方法,并根据所解决问题的特性对遗传算法进行改进:
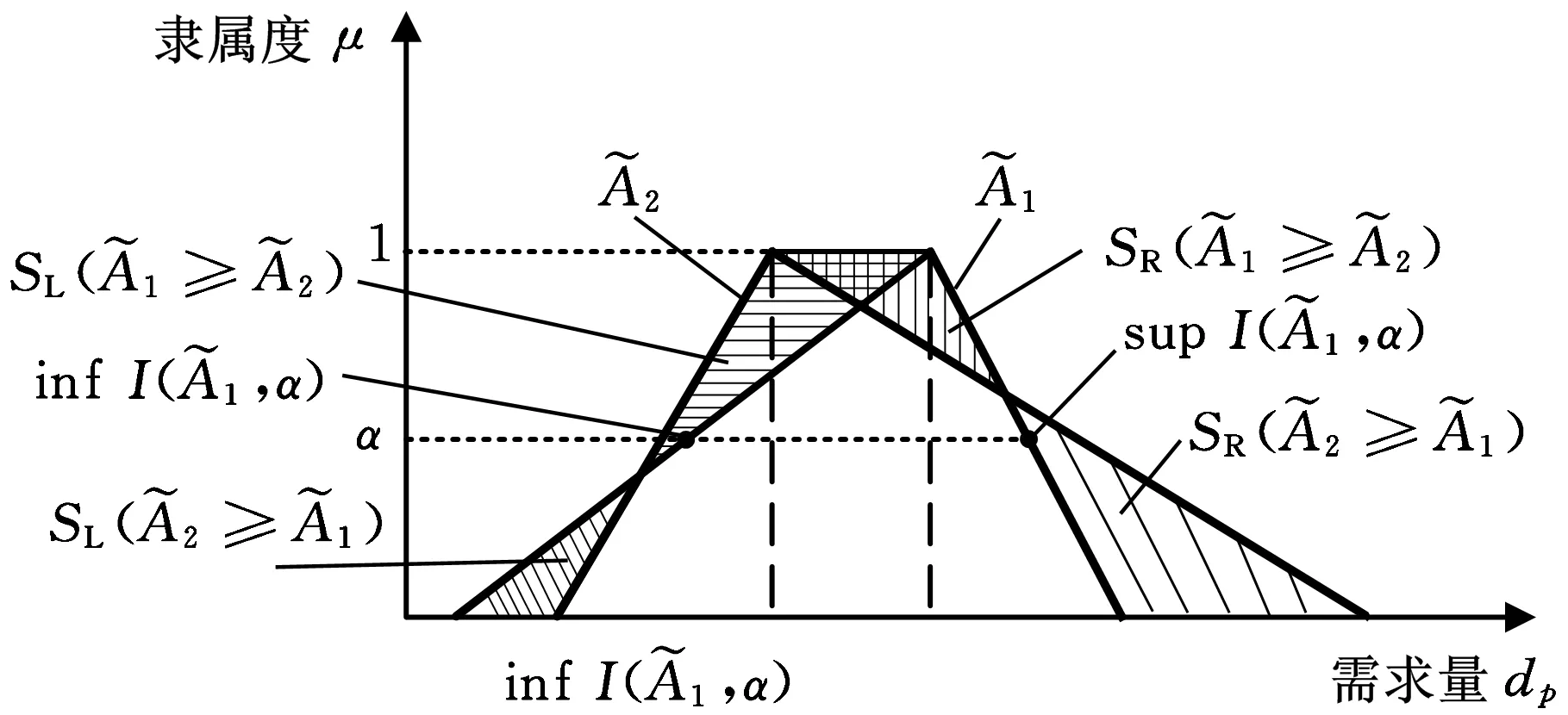
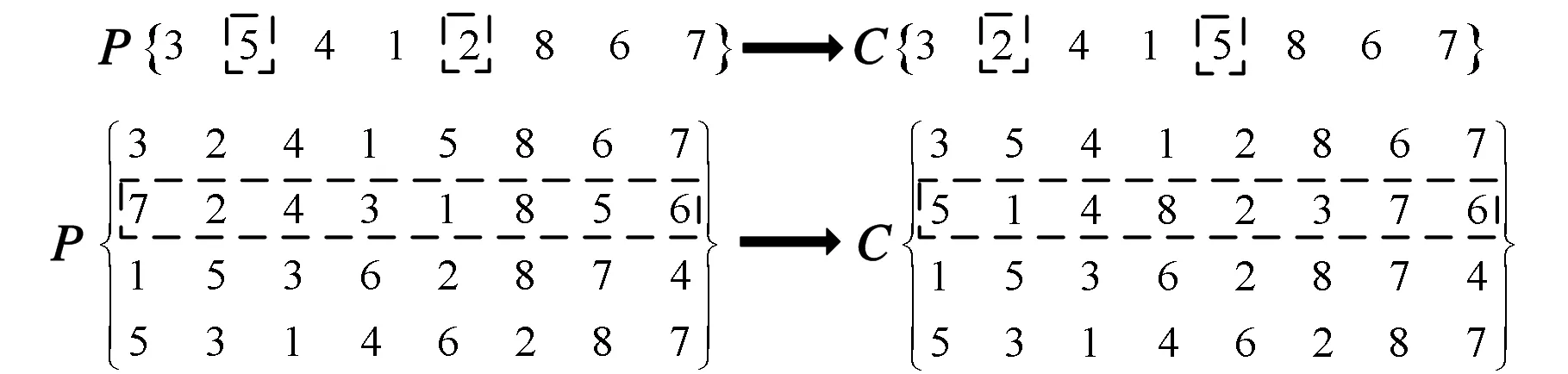
(1)结合三角模糊数字运算和排序方法。遗传算法的目标值计算和比较通常是精确数值运算,但是在上述构建的基于不确定需求的不等面积动态设备布局模型中,作为输入之一的需求数据是三角模糊数字,目标值计算过程涉及模糊运算,目标值的比较亦是模糊数字的大小比较。因此,在遗传算法中引入三角模糊数字计算和排序方法,根据三角模糊数字运算规律计算获得每个可能方案的目标函数值,再按照模糊数字排序方法比较不同方案目标值的大小,完成优胜劣汰过程。
(2)引入自适应局部搜索机制。遗传算法是一种全局搜索进化算法,可有效避免局部收敛,但是在解决大规模复杂问题时存在收敛缓慢问题。引入局部搜索机制既可提升遗传算法收敛速度,又可通过在次优解的领域搜索增加获得最优解的概率[13],是改善遗传算法性能的有效方法。但是局部搜索需要进行大量的运算,将会大大延长求解时间,同时有可能导致局部收敛。因此,本文在遗传算法中引入的是基于相似系数方法[14]的自适应局部搜索机制,并非在每次循环都进行局部搜索,而是通过计算每次遗传循环中种群的平均相似度系数,判断是否需要局部搜索。
改进遗传算法的求解流程如图4所示,具体求解步骤如下。
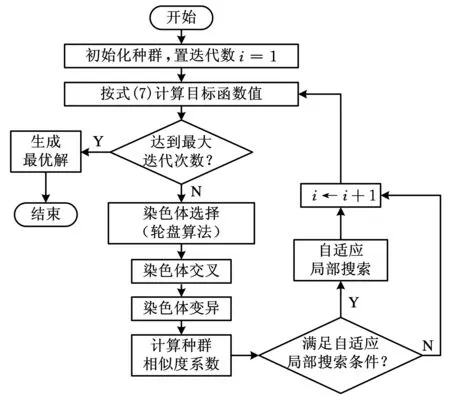
图4 改进遗传算法的求解流程图
(1)迭代数i=0,随机产生初始种群P0,种群规模N0,置P0为当前种群P。
(2)根据式(7)计算当前种群目标值,比较获得当前种群的最优个体并置为当前最优解Be。
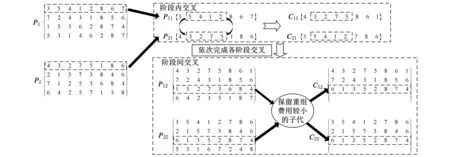
(3)若迭代数i (4)i←i+1,产生新种群Pi。①轮盘算法产生新种群,在当前种群P上随机选择k个染色体,比较其目标值,将较优者复制至新种群Pi;②重复步骤①直至新种群Pi规模为N0;③将新种群Pi随机划分为Ni/2对父代染色体,按概率pc进行交叉操作,被选中的父代染色体在交叉操作完成后由子代染色体取代,未被选中的染色体保留在种群Pi中;④对种群Pi按概率pm进行变异操作;⑤计算种群Pi的相似度系数并判断是否符合局部搜索条件,若符合则对当前种群进行局部搜索。 (5)将新种群Pi置为当前种群P,返回步骤(2)。 2.2三角模糊数运算与排序方法 (8) (9) 根据上述三角模糊数字运算定义,每个方案计算获得的目标值是三角模糊数字,故须比较模糊数字的大小(即模糊数字排序)。目前,在模糊数字排序上尚无公认的最好的方法,出于可靠性和可实施性考虑,本文采用Fortemps等[15]提出的面积比较方法。 (10) (11) (12) (13) 其中 (14) (15) (16) 图5 三角模糊数比较示意图 2.3染色体编码 图6 单阶段布局示意图 在动态环境下,一个动态布局方案由T(T为阶段数)个静态布局方案组成,因此,其染色体编码为T行矩阵,每行为一个单阶段染色体序列,代表一个阶段的静态设备布局。图7所示的车间动态布局方案对应的染色体编码为编码后,每个染色体代表一个动态布局方案,通过交叉、突变和自适应局部搜索等一系列遗传操作完成优胜劣汰过程,最终获得最优解或近最优解。 图7 动态布局示意图 2.4染色体交叉操作 交叉操作包括阶段内染色体交叉(行内交叉)和阶段间染色体交叉(行间交叉)两部分,并按一定概率进行。阶段内染色体交叉以行内的单个设备编码为交叉对象。如图8所示,P11、P21是父代矩阵编码P1、P2对应阶段的编码(即进行交叉操作的两个阶段编码),随机生成两个交叉点,将P11、P21位于两交叉点间的编码逐一交叉,依次对P1、P2各个阶段进行交叉操作。 阶段间染色体交叉以整行编码为交叉对象,在阶段内交叉完成后进行。随机产生交叉点t,将父代P12、P22中t以前阶段的编码保留至子代中,对于子代中t阶段的编码,以子代C12(C22)的t-1阶段到t阶段的重组费用最小为标准,从P12、P22的t阶段中选择重组费用较小的一个作为C12(C22)的t阶段编码,同理产生子代t以后阶段的编码。如图8中,选中的交叉点为3,所以父代中第一、二阶段的编码直接保留至子代C12、C22中。子代C12中第三阶段编码的产生方法为:分别计算C12第二阶段到P12第三阶段和C12第二阶段到P22第三阶段的设备重组费用并比较大小,若前者小,则将P12第三阶段编码复制至C12第三阶段,否则将P22第三阶段编码复制至C12第三阶段。同理产生C12的第四阶段编码和C22的第三、四阶段编码。 图8 染色体交叉操作 2.5染色体突变操作 种群在完成交叉操作后按一定概率进行突变操作,包括阶段内突变和阶段间突变两部分。如图9所示,阶段内突变是在单阶段染色体编码中随机选择两个编码,交换其位置。阶段间突变在阶段内突变之后进行,随机选取突变阶段,将其替换为一个随机产生的染色体编码。 图9 染色体变异操作 2.6自适应局部搜索 本文采用基于相似度系数的自适应性局部搜索。在每次迭代中,计算种群的染色体相似度系数,将种群相似度系数与预定参数比较,对符合条件的种群进行局部搜索。种群相似度系数按文献[14]提出的方法计算,染色体p和q的相似度系数Spq为 (17) (18) 式中,v为染色体中的位置系数;gpv为在染色体p中布置于位置v的设备;∂(gpv,gqv)为判断指数。 按式(18)定义,整个种群的平均相似度系数为 (19) 只有当种群的平均相似度系数大于预定值δ时,方在此次循环中进行局部搜索。 对符合局部搜索条件的种群,先将种群中所有染色体按照式(7)目标函数值升序排列,再根据文献[16]所采用的方法筛选出需进行领域搜索的染色体。这种筛选方法可保证较优和较差的方案均有一定的概率被选中,但是较优的方案有更大的概率被选中,从而保证在加快收敛速度的同时避免局部收敛。 局部搜索的领域结构采用两两交换结构,即在选定的染色体中随机选取某一阶段的任意两个设备,交换其位置。比较交换前后染色体的目标函数值,将较优者保留在种群中,同时记录这两个设备的位置,在之后的λ次搜索中不改变其位置。如果重复θ次搜索之后仍未获得更优的方案,则放弃该染色体搜索,进入下一个选定染色体的局部搜索。 3.1不等面积设备布局问题测试 本文分别就解决不等面积设备静态布局和不确定需求下的动态布局问题与文献案例进行对比分析,从而验证所提方法的有效性。 以文献[17]中的案例(记为算例1)作为测试算例进行求解。算例1中共有12个设备组和一个原料堆放组,各个设备的尺寸不等,设备尺寸和物流量等相关信息在文献[17]中均有详述。取种群规模N0=100,交叉概率pc=0.8,突变概率pm=0.3,最大迭代数imax=100,在CPU主频2.2 GHz,内存4 G,Window 7操作系统下进行求解。获得最优解的布局方案如图10所示,图11为算法收敛图。 图10 算例1布局方案图 图11 算例1收敛图 由图11可看出,采用本文提出的改进遗传算法能够在有限的迭代次数内获得最优解或近最优解,并能有效避免局部收敛。两种算法运算结果对比列于表1,由于在遗传算法中增加了自适应局部搜索,搜索方向性更强,因此能够在较少的迭代次数中获得最优解。 表1 算例1两种算法运算结果对比 3.2不确定需求下的动态布局问题测试 算例1验证了所提算法在解决不等面积设备布局问题的有效性,为进一步验证算法解决不确定需求下设备动态布局的有效性,采用文献[7]的案例进行测试。文献[7]采用遗传算法解决不确定需求环境下的动态布局问题,但是布局模型是离散式模型,共有3个案例,选取其中含有12个设备(记为算例2)和30个设备(记为算例3)的两个算例进行求解,两种方法获得的结果如表2所示。 表2 算例2和算例3的两种算法结果对比 由表2可知,在算例2和算例3中,改进遗传算法均能获得较优方案,这是因为引入自适应局部搜索,在次优解的领域进行搜索,增加了获得更优解的概率。 4.1实例概述 为了从整体上更全面地验证本文所提方法的有效性和实用性,以发动机缸盖加工车间为实例,在不确定需求环境下进行动态布局规划。 某发动机厂拟新建一加工车间,需确定12个设备组的布局位置,设备组尺寸及单位距离重组费用如表3所示。该车间计划用于生产H1、H2、H3三种类型的缸盖,三种产品的单位物流量矩阵已知,在可预见的各个生产阶段的预测产量如表4所示。车间为34 m×28 m的矩形场地,相邻设备间横向最小间距h=1.5 m,纵向最小行间距s=2 m,设备与车间边界横向最小距离so x=2 m,纵向最小距离soy=2 m。 表3 设备尺寸信息 表4 产品预测需求量 件 4.2不确定需求描述 4.3算法参数设计及问题求解 根据车间实际约束要求,按照1.2节构建多行线性设备布局模型。优化算法的参数设置如下:种群规模200,交叉概率0.85,变异概率0.3;自适应局部搜索的相关参数设置δ=0.6,λ=20,θ=60。以式(7)为优化目标,对实例问题进行求解。获得方案总费用值用三角模糊数表示为(3.85×107,4.16×107,4.45×107),布局方案如图12所示,图13是求解过程的算法收敛图。 图12 动态布局方案图 图13 实例求解过程收敛图 4.4结果分析 实例问题如果采用静态布局方法求解,获得的最优方案物料搬运费用值为4.26×107kg·m,而采用本文所提出的方法获得的模糊总费用值为(3.85×107,4.16×107,4.45×107)kg·m,可看出,两种方案的费用值基本在一个数值范围内且本文所提方法的结果更优一些,由此可说明获得的动态布局方案是一个有效方案。在图12所示的动态布局方案中,设备根据实际尺寸在布局空间中分行布置,满足设备间距和行间距要求,比较容易转化为实际应用。由图13可看出,由于引入自适应局部搜索,求解过程可较迅速地搜索到最优解或近最优解,从整体上验证了所提出的方法在解决不确定需求下不等面积设备动态布局问题的有效性和实用性。 在动态布局规划中考虑需求不确定性的影响是为了提升布局在面对未来产品需求波动时的性能稳定性,以节省生产过程中的物料搬运费用。为进一步验证所获得的布局方案在面对未来需求波动时的性能,通过随机产生需求数据以模拟未来的需求波动,计算总费用值,以静态布局方案为参照进行验证。随机产品需求数据列于表5,对应的总费用值列于表6。表5中,(1100,120,3000)指产品H1在生产阶段1、2、3的需求分别为1100、120、3000。 表5 测试需求数据 件 表6 测试结果 kg·m 由表6可看出,在5组数据测试结果中,本文所提出方法获得的布局方案较优的有4组(加粗),说明本文提出的方法可以获得较高鲁棒性的动态布局方案,应对未来需求波动时性能稳定。 传统车间设备布局方法假设产品需求信息确定、物流量固定不变,忽视通过预测获得的需求信息的不确定性及其随时间增大特性的影响。本文针对现有布局方法存在的不足,从更利于转化为生产实际应用的角度出发,以基于柔性区域结构并增加设备间距约束的多行线性布局为基础,构建不确定需求下的不等面积设备动态布局模型。在此基础上,引入三角模糊数运算与排序方法和自适应局部搜索机制对遗传算法进行改进,提出改进遗传算法。分别就不等面积设备静态布局问题和不确定需求动态布局问题分别验证所提算法的有效性。再以某发动机缸盖加工车间为实例,应用本文提出的方法获得不确定需求下的动态布局方案,从整体上验证所提方法的有效性和实用性。车间设备布局有较多评价指标,本文仅以物料搬运和设备重组费用为优化目标进行求解,在今后的研究中,可以着重研究不确定需求下设备动态布局的多目标优化技术,也可以进一步提升算法的搜索效率以解决大规模设备布局问题。 [1]Tompkins J A. Facilities Planning[M]. Hoboken:John Wiley & Sons, 2010. [2]Jr McKendall A R, Liu W H. New Tabu Search Heuristics for the Dynamic Facility Layout Problem[J]. International Journal of Production Research, 2012, 50(3): 867-878. [3]Hosseini-Nasab H, Emami L. A Hybrid Particle Swarm Optimisation for Dynamic Facility Layout Problem[J]. International Journal of Production Research, 2013, 51(14): 4325-4335. [4]祝恒云,叶文华. 模拟退火粒子群算法在动态单元布局中的应用[J]. 中国机械工程,2009,20(2):181-185. Zhu Hengyun, Ye Wenhua. Application of Particle Swarm Algorithm Based on Simulated Annealing in Variable Cellular Facility Layout Problems[J]. China Mechanical Engineering,2009,20(2):181-185. [5]Balakrishnan J, Hung Cheng C. The Dynamic Plant Layout Problem: Incorporating Rolling Horizons and Forecast Uncertainty[J]. Omega, 2009, 37(1): 165-177. [6]Samarghandi H, Taabayan P, Behroozi M. Metaheuristics for Fuzzy Dynamic Facility Layout Problem with Unequal Area Constraints and Closeness Ratings[J]. The International Journal of Advanced Manufacturing Technology, 2013, 67(9/12): 2701-2715. [7]Drira A, Pierreval H, Hajri-Gabouj S. Design of a Robust Layout with Information Uncertainty Increasing Over Time: a Fuzzy Evolutionaryapproach[J]. Engineering Applications of Artificial Intelligence, 2013, 26(3):1052. [8]McKendall A R, Hakobyan A. Heuristics for the Dynamic Facility Layout Problem with Unequal-area Departments[J]. European Journal of Operational Research, 2010,201(1):171-82. [9]Mazinani M, Abedzadeh M, Mohebali N. Dynamic Facility Layout Problem Based on Flexible Bay Structure and Solving by Genetic Algorithm[J]. The International Journal of Advanced Manufacturing Technology, 2013,65(5):929-43. [10]Drira A, Pierreval H, Hajri-Gabouj S. Facility Layout Problems: a Survey[J]. Annual Reviews in Control, 2007,31(2):255-67. [11]Kulturel-Konak S. A Linear Programming Embedded Probabilistic Tabu Search for the Unequal-area Facility Layout Problem with Flexible Bays[J]. European Journal of Operational Research, 2012,223(3):614-25. [12]周娜,宓为建,徐子奇,等. 基于改进型自适应遗传算法求解设备多行布局问题[J]. 上海交通大学学报,2013,47(12):1924-1929. Zhou Na, Mi Weijian, Xu Ziqi,et al. Solution to Multi-line Layout Problems of Equipment Based on Improved Adaptive Genetic Algorithm[J]. Journal of Shanhai Jiaotong University,2013,47(12):1924-1929. [13]Ripon K S N, Glette K, H∅vin M, et al. An Adaptive Local Search Based Genetic Algorithm for Solving Multi-objective Facility Layout Problem[M]. Berlin: Springer, 2010. [14] Yun Y, Moon C, Kim D. Hybrid Genetic Algorithm with Adaptive Local Search Scheme for Solving Multistage-based Supply Chain Problems[J]. Computers & Industrial Engineering,2009,56(3):821-38. [15]Fortemps P, Roubens M. Ranking and Defuzzification Methods Based on Area Compensation[J]. Fuzzy Sets and Systems, 1996, 82(3): 319-330. [16]Rochat Y, Taillard É D. Probabilistic Diversification and Intensification in Local Search for Vehicle Routing[J]. Journal of Heuristics,1995,1(1):147-67. [17]郭源源, 王谦, 梁峰. 基于粒子群优化算法的车间布局设计[J]. 计算机集成制造系统,2012,18(11):2476-2484. Guo Yuanyuan, Wang Qian, Liang Feng. Facility Layout Design Based on Particle Swarm Optimization[J]. Computer Integrated Manufacture systems, 2012, 18(11):2476-2484. (编辑袁兴玲) Dynamic Facility Layout Method under Uncertain Product Demands Ma ShumeiCai HuisenZhang YifanLi Aiping Tongji University,Shanghai,201804 The dynamic facility layout method combined with fuzzy set theory and improved genetic algorithm was brought out on the basis of considering the influences of uncertain product demands, aiming at the deficiency of the present dynamic facility layout method. The characteristics of product demand uncertainty change over time were analyzed, and the uncertain demands were described by the triangular fuzzy numbers. The dynamic layout was transformed into several static layouts through analyzed facility relocation process between each period so as to establish a dynamic facility layout model under uncertain demands based on flexible bays structure. An improved genetic algorithm was proposed by combined triangular fuzzy number operation and adaptive local search with genetic algorithm, and then solved dynamic facility layout problems with uncertain product demands and unequal area constraints; the target of the problem was minimum the total cost of material handling and facility relocation. At last,the examples were illustrated to verify the practicability and effectiveness of the given method. uncertain demand; improved genetic algorithm; unequal area; dynamic facility layout 2014-12-23 国家科技重大专项(2013ZX04012-071) TH165< class="emphasis_italic">DOI :10.3969/j.issn.1004-132X.2015.11.012 马淑梅,女,1967年生。同济大学机械与能源工程学院副教授、博士。主要研究方向为数字化设计与制造、逆向工程技术及快速原型制造技术等。蔡惠森,男,1990年生。同济大学机械与能源工程学院硕士研究生。张一帆,男,1992年生。同济大学机械与能源工程学院硕士研究生。李爱平,女,1951年生。同济大学机械与能源工程学院教授、博士研究生导师。

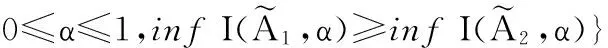
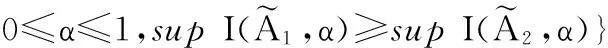

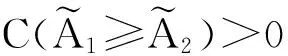

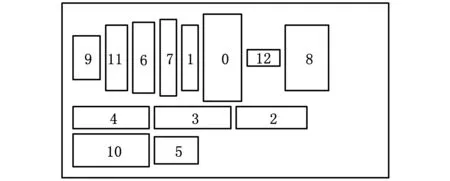
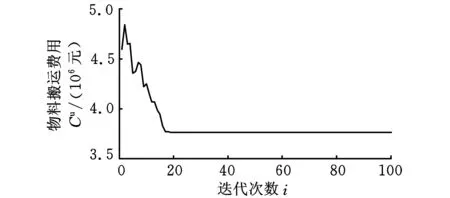
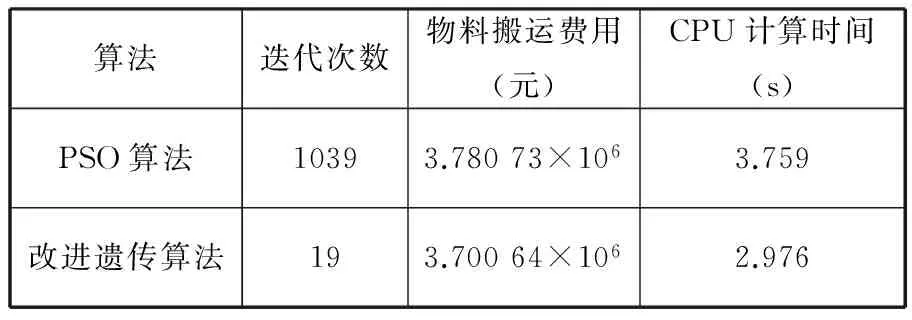
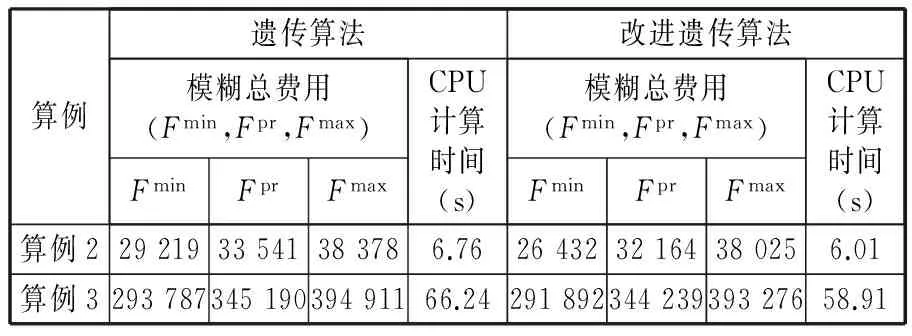
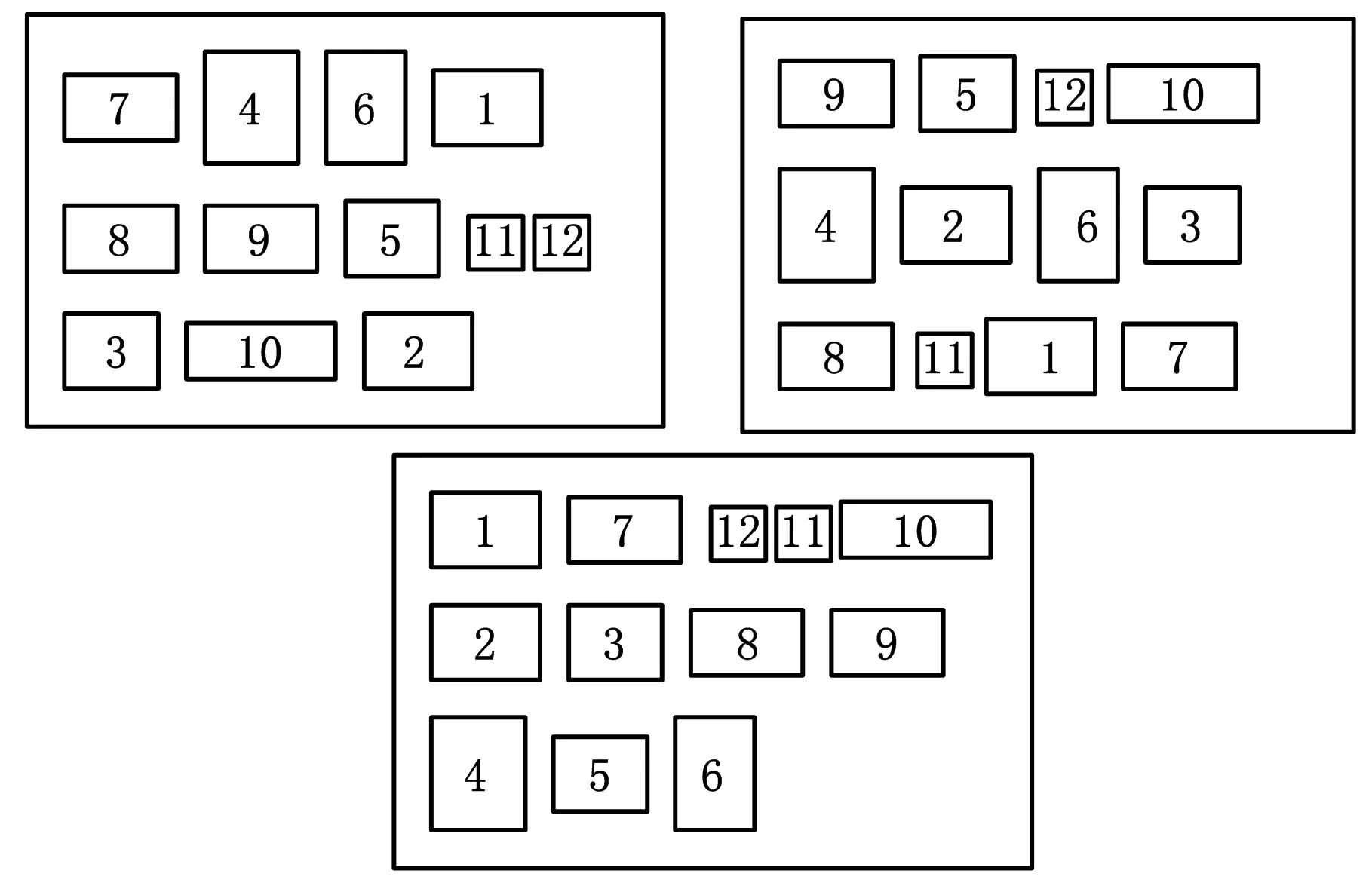
3 算例测试
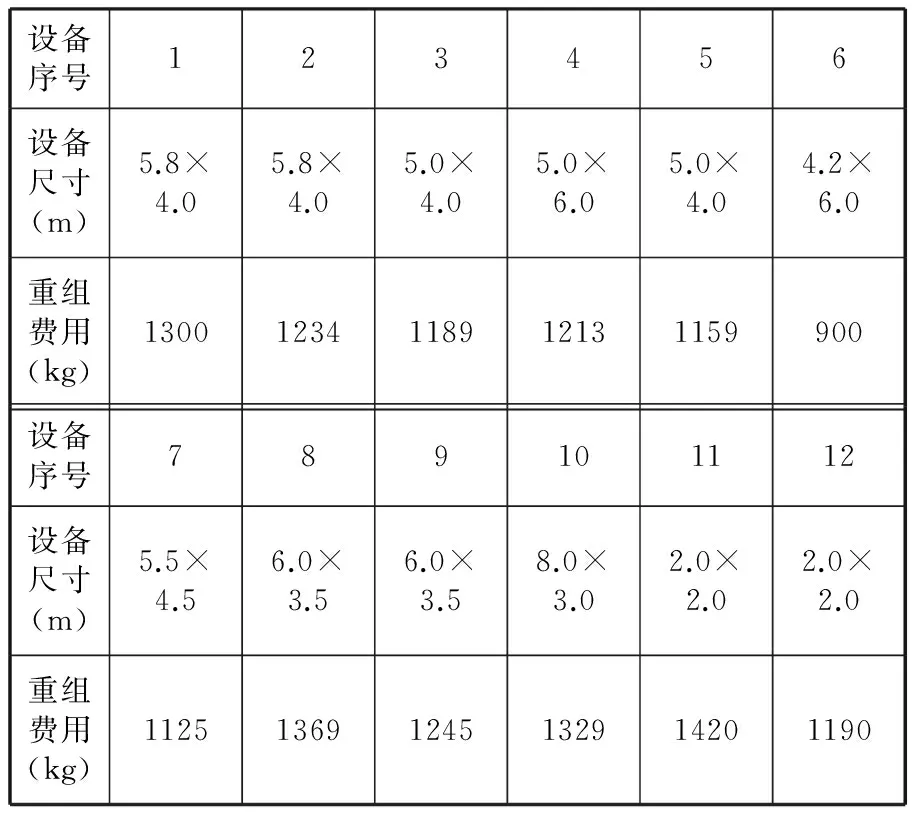
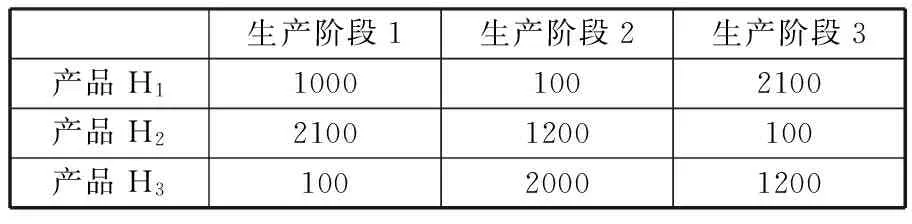
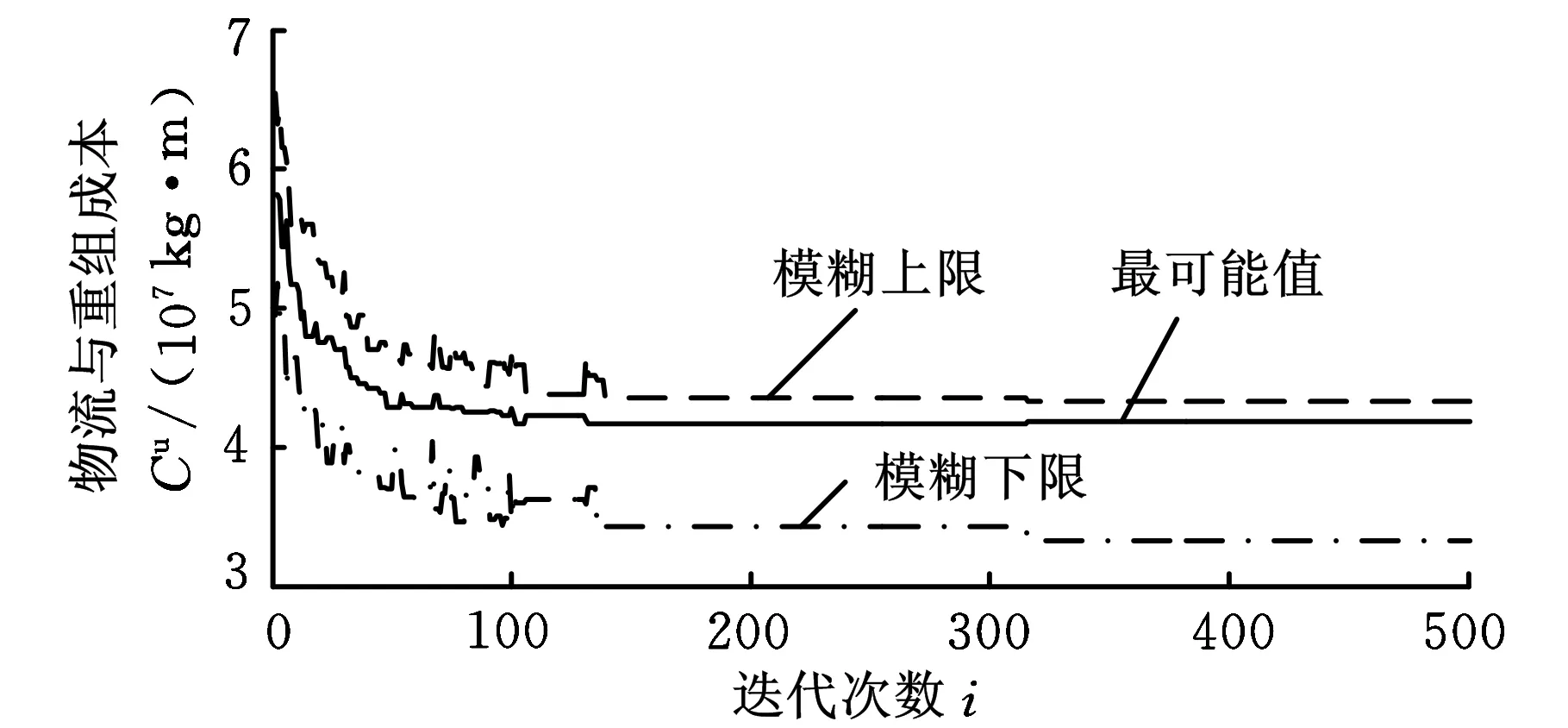
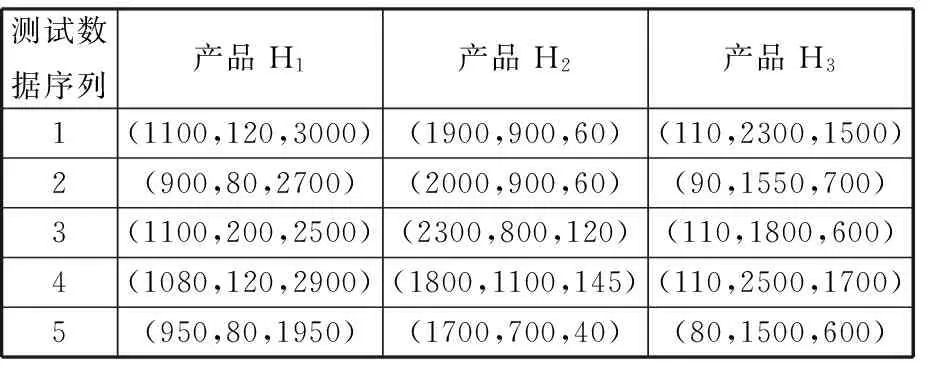
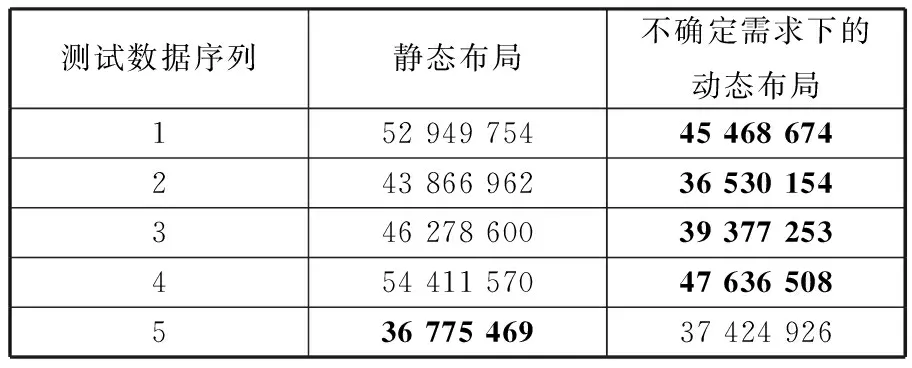
4 实例分析
5 结束语
