考虑不完全保护的复杂系统可靠性评估
2015-10-29阮渊鹏
阮渊鹏 李 晓 崔 剑
杭州电子科技大学,杭州, 310018
考虑不完全保护的复杂系统可靠性评估
阮渊鹏李晓崔剑
杭州电子科技大学,杭州, 310018
鉴于已有研究在处理由部件失效传播引起的共因失效的复杂系统可靠性评估问题时存在的缺陷,借鉴元胞自动机并行计算的优势以及蒙特卡罗模拟技术在处理复杂问题中的灵活性,提出了一种基于元胞自动机思想的蒙特卡罗模拟方法,该方法考虑了不完全保护对系统可靠性产生的影响,不受系统结构、部件数目的限制。最后,通过两个算例分别说明了该方法的正确性以及在可靠性分析中的具体应用。
复杂系统;失效传播;不完全保护;元胞自动机;蒙特卡罗模拟
0 引言
为了更好地适应实际工程的需要,可靠性评估问题的研究对象逐渐由单个部件转化到整个系统。而对于系统可靠性评估问题而言,系统结构的复杂化、系统部件数量的规模化以及部件存在关联性等也使得研究对象逐渐从简单系统深化到复杂系统。
文献[1-5]研究了较为复杂系统的可靠性,其重点在于如何提高算法的效率,以降低算法的时间复杂度以及空间复杂度。当系统结构十分复杂、部件数目很多时,精确解析方法的计算将变得繁琐,因此,针对这类系统,许多近似方法被广为应用,这类方法主要包括定界法和仿真分析方法两种类型。由于定界法不能有效地平衡计算精度与计算效率[6],故仿真分析方法一直受到很多学者的青睐,其中,最为经典的当属蒙特卡罗模拟(Monte Carlo simulation,MCS)方法。当MCS法应用到系统可靠性评估过程中时,最为重要的一步是如何判断系统对应网络的连通性。传统的MCS法[7-8]都是基于最小路集/割集或基于图论中提到的深度优先搜索算法(depth first search,DFS)与广度优先搜索算法(breadth first search,BFS)来判断网络的连通性,Rocco等[6]指出,上述判断网络连通性的方法都会导致NP问题。元胞自动机(cellular automata,CA)作为一种离散系统仿真的方法,由于其在判断网络连通性问题上具有并行运算的优势,因此,在近几年被广泛应用到复杂系统的可靠性评估问题当中[6,9-11]。
上述文献都着眼于算法的效率或精确度,未考虑部件之间的关联性,认为各部件的失效与否是不相关的,即各部件的“失效事件”是相互独立的。但是,如文献[12]所述,现实工程中,许多系统的部件之间存在一定的相关性。部件间的相关性有许多类型,包括共因失效、功能相关、载荷共享等[12]。本文仅研究共因失效对复杂系统可靠性的影响,对于此类问题,现有的研究可以大致分为两类。一类是外部环境导致的共因失效对系统可靠性的影响,另一类是部件的失效传播对系统可靠性的影响。对于第一类问题,现有的研究已较为成熟[13-15]。
针对第二类问题,现有的研究[16-19]或多或少存在一些缺陷。①提出的组合算法在系统结构复杂并且能引起失效传播的部件数目较多时,或是无能为力,或是效率较低,易引起组合爆炸;②未考虑不完全保护的影响。失效保护[20]指的是由于部件存在一定的保护机制,使得其在遭受由其他部件引起的失效传播时不受影响。失效保护分为个体保护与群体保护两类。个体保护是指部件自身具备一定的保护能力,群体保护是指多个部件受同一保护机制的影响,形成了失效保护群,当这一保护机制失效时,失效保护群中所有部件将不能被保护,个体保护是群体保护的特例。若个体保护或群体保护存在一定的失效概率,则称其为不完全保护。
文献[21-22]提出了基于MCS与CA的算法,并应用于复杂二态系统的可靠性评估问题当中,但是该研究未考虑不完全保护的影响。文献[20]考虑了不完全保护的影响,将发生函数法应用到多态系统的可靠性评估问题当中,但是,该方法仍不能有效处理前文所说的第一类缺陷。文献[23]提出了一种基于MCS的方法,能有效解决多态情况下随机流网络的可靠性评估问题,并考虑了不完全保护的影响。针对系统结构复杂、部件数目较多、系统存在部件失效传播以及不完全保护的情况,本文提出了一种基于MCS与CA的有效评估该种情况下系统可靠性的方法。
1 问题描述与基本假设
1.1问题描述
如图1所示,系统的可靠性框图可以转化成网络G=(N,A),N表示网络中n个节点的集合,而A表示网络中m个边的集合,每条边代表一个部件,边的状态为0(失效)或1(正常),即系统对应的部件是二态的。系统的可靠性可以转化为网络的可靠性,而网络的可靠性可进一步转化为网络两端点S与T连通的概率,对于这个问题的求解,文献[6,9-11]利用CA解决复杂网络连通性的优势,有效解决了网络结构复杂、边数较多情况下的可靠性评估问题。
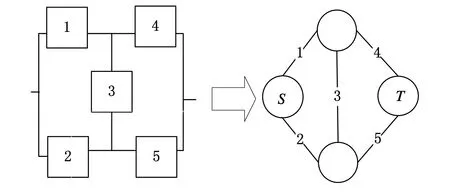
图1 系统转化为网络
本文同时考虑了失效传播及不完全保护对于系统可靠性的影响,这种影响可以从两方面得以体现,一是某条边(部件)的失效有可能会引起其他边发生失效,二是在某条边受其他边失效传播影响时,其失效保护群会发挥一定的保护作用,使其免受损害。因此,若部件不独立,则文献[6,9-11]中提出的一些方法在该种情况下不适用。
1.2问题基本假设
对于考虑部件失效传播及不完全保护的复杂系统,本文作了以下几个基本假设:
(1)部件本身存在“失效”与“正常”两种状态。它的“失效”状态(即状态为0)可能由三种情况引起,一是受自身“共因失效”影响,二是受其他部件“共因失效”带来的失效传播影响,三是受只影响自身的“独立失效”影响。
(2)系统也存在“失效”与“正常”两种状态。系统是否失效取得于两方面因素,一是系统的结构,二是组成系统的各部件对应的状态。如果用系统对应网络来表示的话,系统是否失效便取决于网络两端点是否连通。
(3)各部件“独立失效”事件之间相互独立。
(4)存在失效传播部件的“共因失效”事件之间相互独立,并且部件在受其他部件“共因失效”事件作用时自身的“共因失效”事件也能触发。
(5)同一部件不存在于不同的失效保护群。
(6)“失效保护”事件只有在其对应失效保护群里的部件受其他不属于此保护群的部件“共因失效”事件作用时才可能触发,并且不同失效保护群对应“失效保护”事件是相互独立的。
(7)部件在受自身触发的“共因失效”事件作用时, 不管其是否在失效保护群里,都失效。
(8)部件在受其他部件“共因失效”事件作用时,若这两个部件属于同一失效保护群,则不管其对应失效保护群“失效保护”事件是否触发,该部件都失效。
2 算法提出
2.1算法基本思想
针对已有方法的缺陷,本文提出了一种基于MCS与CA的计算复杂系统可靠性的方法。如图2所示,该算法的基本思想是:首先将系统可靠性框图转化成二终端网络,然后根据基本假设中提到的关于“共因失效”与“失效保护”事件的触发条件,并结合部件对应的可靠度条件概率进行每一次仿真,用CA判断每次仿真对应网络的连通性,最后计算网络可靠度。
2.2CA判断网络连通性
CA应用的基本思想是:将图1所示网络的每个节点看作一个元胞,其对应的状态是1(激活)或0(未激活),各节点在时刻t的状态由与其相连的各节点(邻居)在时刻t-1的状态决定,若邻居中至少存在一个节点在时刻t-1的状态为1,则该节点在时刻t的状态为1。元胞随时间变化的规则可以用关联函数
w(i,t+1)=OR(w(j,t),…,w(k,t)),
(1)
来表示。其中,w(i,t+1)表示节点i在时刻t+1的状态,j,…,k∈Ei,Ei表示节点i的邻居,定义Ei={j∈N且(j,i)∈A}。若在经过数次迭代之后,端点T被激活,则表示网络是连通的,否则,不连通。由迭代过程可知,判断网络是否连通的迭代次数不会超过n-1,因此,CA算法的时间复杂度为O(n)。
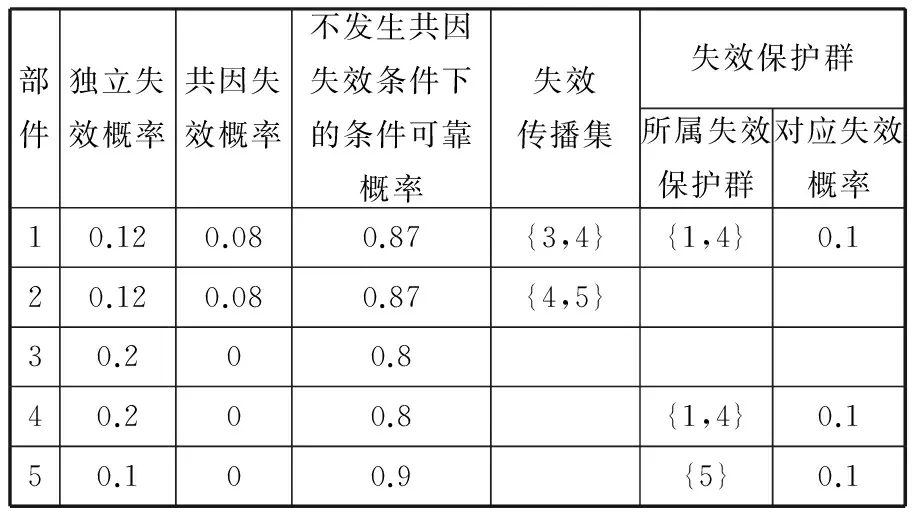
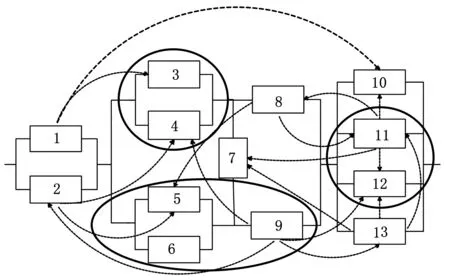
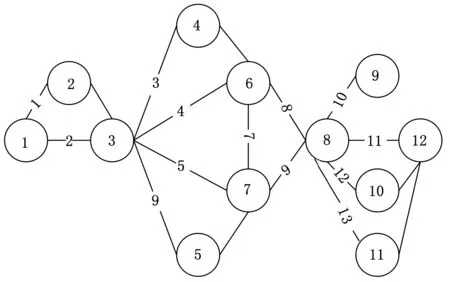
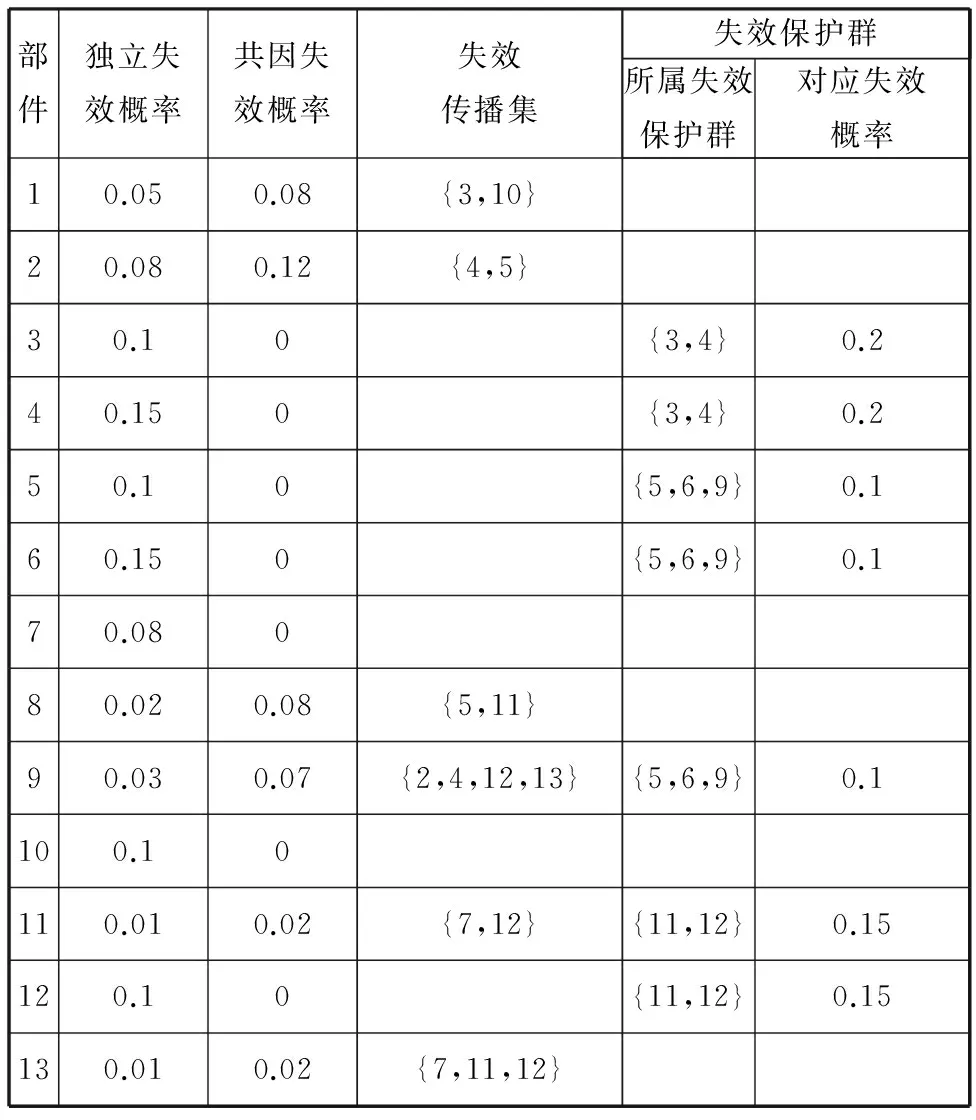
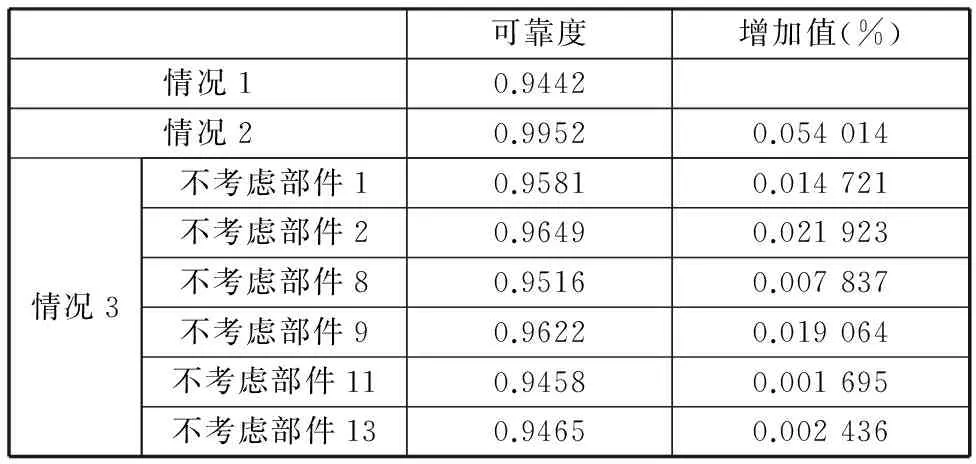
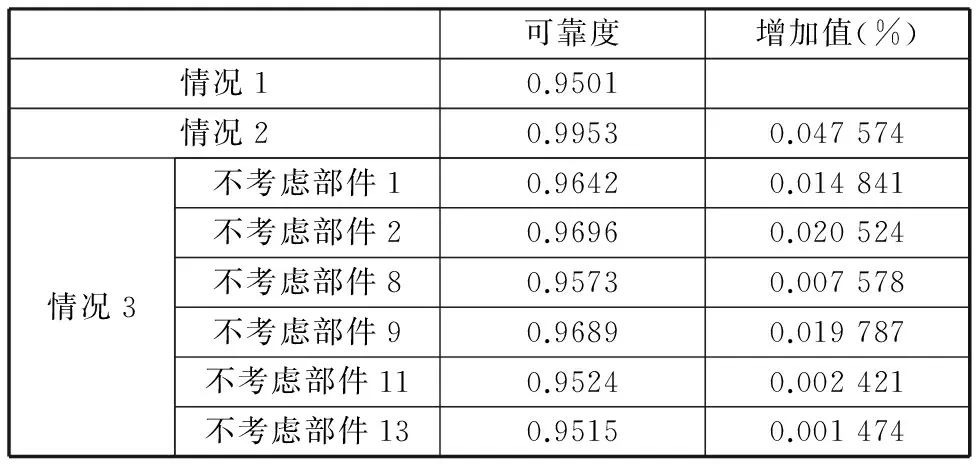
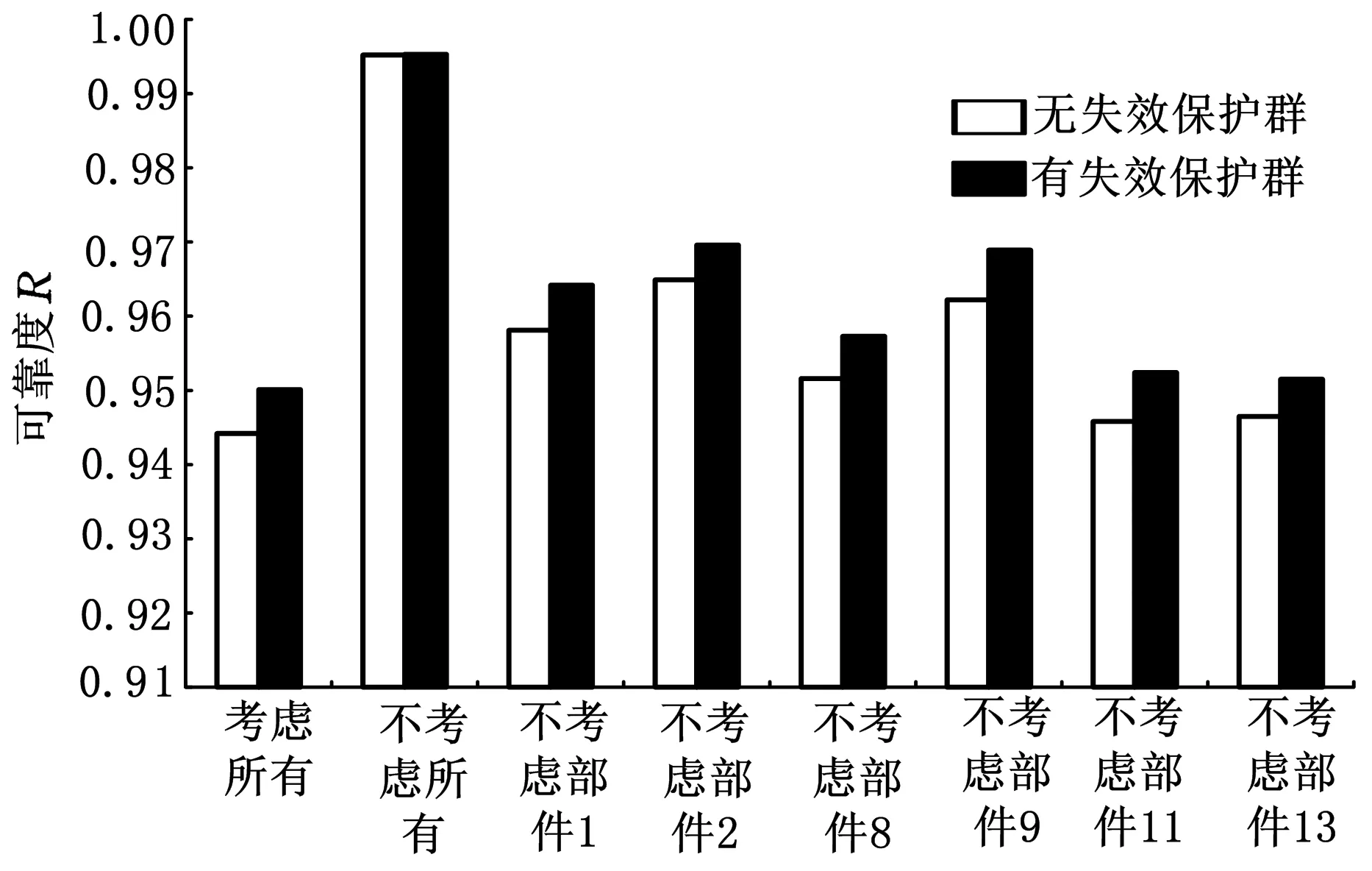
CA判断网络连通性的具体步骤[20-21]如下:①初始时刻t=0;②设置所有元胞的初始状态都为0;③设置源点S的状态为1,即w(1,0)=1;④时刻t←t+1;⑤按照关联函数式(1)更新所有元胞的状态;⑥如果w(T,t)=1,算法结束,输出c=1,即表示节点S到节点T是连通的;⑦否则,假如t 2.3具体步骤 所提算法需要输入的参数和条件如下:仿真循环次数M、系统可靠性框图、存在失效传播的部件编号(i1,i2,…,iL)、对应的共因失效概率(pci1,pci2,…,pciL)、独立失效概率(pi1,pi2,…,piL)、可靠概率(qi1,qi2,…,qiL)、失效传播集(Ci1,Ci2,…,CiL)、失效保护群PGj(j=1,2,…,F)及各失效保护群对应的保护失效概率pG1,pG2,…,pGF,其余不存在失效传播的部件对应的独立失效概率及可靠概率。 算法的具体步骤如下。 (1)将系统的可靠性框图转化成网络。冗余子系统需要经过特殊处理,保留一个部件,然后将其余部件都转化成两个部件,一个是和原部件相同的部件,另一个是失效概率为0的虚拟部件,如图3所示。图3中,左边部分是冗余子系统的可靠性框图,右边部分是转化后的网络图,网络图中的边1,2,…,n代表的是部件1,2,…,n,而1′,2′,…,(n-1)′代表失效概率为0的虚拟部件,部件n没有虚拟部件。 图3 冗余系统网络转换 (2)循环次数m的初始值为1,网络连通次数c的初始值为0。 (3)初始网络G=(N,A)对应各边的初始状态都为1。 (4)各边失效传播集用Cij表示,例如,若部件1发生“共因失效”事件,失效会传播给部件2、3,则部件1对应的失效传播集为C1={2,3}。每个失效保护群用PGj(j=1,2,…,F)表示,例如,若第一个失效保护群由部件2、3组成,则失效保护群可以表示为PG1={2,3}。 (5)对于各失效保护群分别产生随机数r,若r≤pGj,j=1,2,…,F,则说明对应的失效保护群发生失效,即未触动“失效保护”事件,反之,则触动“失效保护”事件。 (6)对于会引起失效传播的部件分别产生随机数r,若r>1-pcij,j=1,2,...,L,则此部件发生“共因失效”事件。若部件满足以下任意一种情况:①部件触发“共因失效”事件;②部件受其余部件“共因失效”事件影响,并且不属于任何失效保护群或对应失效保护群失效;③部件受其余部件“共因失效”事件影响,对应保护群触发“失效保护”事件,但至少有一个对其进行失效传播的部件与其属于同一个失效保护群。则其在初始网络G中对应边的状态值由1转化为0,从而形成新的网络G1=(N1,A1),该网络将剔除初始网络G中状态值为0的边。 (8)对于网络G1=(N1,A1)中的每个边,分别产生一个随机数r,若其值大于其条件可靠概率,则该边的状态值由1变为0,最终生成新的网络G2=(N2,A2)。 (9)用CA算法判断网络G2节点S到节点T的连通性,并得出c值,c=1表示网络连通,c=0表示网络不连通。 (10)若c=1,c←c+1。 (11)若循环次数m (12)否则,计算网络可靠度:R=c/M。 2.4算法结果分析 本文采用文献[18,20]中给出的两个例子对提出算法进行应用说明和验证。由于该例子中系统的结构不能转化为串联或并联结构,因此,文献[18,20]中提出的发生函数法不适用于该系统的可靠性评估问题,而文献[19]中提出的故障树与组合算法的集成算法未考虑不完全保护对于系统可靠性产生的影响,且当能引起失效传播的部件数量较多时,该方法会引发“组合爆炸”问题。本文提出方法考虑了不完全保护对于系统可靠性的影响,可以计算任意复杂结构的系统可靠度,也不会因为能引起失效传播的部件或不完全保护群的数量较多而引发“组合爆炸”问题。 3.1算例一 某工业生产模块由5个部件组成:2个泵设备(部件1、2)以及3个反应器(部件3、4、5)。部件1、2 并联,并与部件3、4、5 组成的并联子系统串联,系统可靠性框图见图4。第一个泵设备(部件1)失效引起的火灾可以使反应器3、4失效,第二个泵设备(部件2)失效引起的火灾可以使反应器4、5失效,因此,部件1、2 能引起失效传播。如图4a所示,带箭头的虚线表示部件对应的失效传播集,椭圆表示的是失效保护群。 (a)系统可靠性框图 (b)系统对应网络图图4 系统可靠性框图转化为系统网络图 将系统可靠性框图转化为网络图,网络图上已标注的每个边表示系统每一个部件,其余未标注的边表示虚拟部件,其可靠性是1,且不受任何其他部件失效传播的影响。部件对应的基本信息如表1所示。 表1 算例一部件基本信息 分别用文献[18,20]中提到的发生函数法与本文中提出的算法进行计算,仿真循环次数M=100 000,计算结果如表2所示。 表2 两种方法的结果比较 由于相对误差率绝对值只有0.12%,因此,可以验证本文提出算法是正确的。 3.2算例二 如图5所示,系统由13个部件组成,存在冗余子系统。带箭头的虚线部分表示每个能引起共因失效的部件的失效传播集,能引起共因失效的部件有部件1、2、8、9、11、13。椭圆表示的是失效保护群,系统存在三个失效保护群,失效保护群1对应部件3、4,失效保护群2对应部件5、6、9,失效保护群3对应部件11、12,每个失效保护群对应一定的失效概率。 图5 系统可靠性框图 首先将可靠性框图转化为网络图,如图6所示。部件对应的基本信息如表3所示。 图6 系统网络图 部件独立失效概率共因失效概率失效传播集失效保护群所属失效保护群对应失效概率10.050.08{3,10}20.080.12{4,5}30.10{3,4}0.240.150{3,4}0.250.10{5,6,9}0.160.150{5,6,9}0.170.08080.020.08{5,11}90.030.07{2,4,12,13}{5,6,9}0.1100.10110.010.02{7,12}{11,12}0.15120.10{11,12}0.15130.010.02{7,11,12} 假设仿真循环次数M=100 000,表4、表5分别给出了有失效保护群时以及无失效保护群时下列三种情况下的系统可靠度值:①考虑所有共因失效影响;②不考虑所有共因失效影响;③不考虑某一部件引起的共因失效的影响。 表4 无失效保护群时的计算结果 表5 有失效保护群时的计算结果 由于仿真循环次数达到了100 000,而对应系统的可靠度水平都较高(大于0.9),因此,结果误差很小,不会对分析造成影响。 由图7可知,在不考虑所有共因失效影响的情况下,失效保护群是否存在对系统可靠度没有任何影响,因此,其对应的系统可靠度值基本相等(不完全相等是因为模拟误差的存在)。而在其余7种情况下,系统可靠度在有失效保护群时要大于无失效保护群时,这也说明了失效保护群引起的“失效保护”事件能提高存在部件失效传播的系统的可靠度。 图7 结果比较 无论有失效保护群还是无失效保护群,情况2(不考虑所有共因失效影响)对应的可靠度值远大于其他情况,情况1(考虑所有共因失效影响)对应的可靠度值最小,而情况3(不考虑某一部件引起的共因失效影响)中,不考虑部件2引起的共因失效的情况对应的可靠度值大于情况3中的其他5种情况。情况1与情况2的结果说明了如果忽略共因失效的影响会高估系统的可靠度,从而误导工程人员作出系统可靠性满足实际需求的错误判断,另外,这也说明了减少或消除由部件引起的共因失效能较大幅度地增加系统的可靠度。对情况3的结果进行分析,可以看出,消除部件2的共因失效可以最大程度地提高系统的可靠度。 通过结果分析,可以发现,影响系统可靠性的因素除系统本身的结构以及部件对应的可靠性以外,“共因失效”事件及“失效保护”事件也是需要考虑的重要因素。评估系统可靠性的主要目的在于分析各因素对系统可靠性的影响,然后制定出改进系统可靠性的合理措施。若不考虑资源、成本限制,改进系统可靠性的措施可以是:①增加系统的冗余结构;②提高部件可靠性;③减少或消除由部件引起的共因失效;④建立失效保护机制,减少失效保护群的失效概率。如果考虑资源、成本限制,则需要找出最优的解决方案,这时应优先消除部件2引起的共因失效。 本文提出了对考虑失效传播及不完全保护的复杂系统进行可靠性评估的MCS-CA集成算法,该算法借鉴了CA在判断网络连通性时的优势,并结合MCS在处理复杂问题时的灵活性,有效解决了已有研究存在的两点缺陷。在此基础上,本文最终通过两个算例说明了算法在实际中的应用。算例一用来验证本文提出算法的正确性,算例二的结果表明,在考虑资源、成本限制下,本文提出算法能为制定改进系统可靠性的有效措施提供帮助,具有一定的理论与实践意义。 [1]Lin Y K.Reliability of a Computer Network in Case Capacity Weight Varying with Arcs, Nodes and Types of Commodity [J]. Reliability Engineering & System Safety, 2007, 92(5): 646-652. [2]Dohmen K. Inclusion-exclusion and Network Reliability [J]. The Electronic Journal of Combinatorics, 1998, 5(1): 1-8. [3]Fratta L, Montanari U. A Boolean Algebra Method for Computing the Terminal Reliability in a Communication Network[J].IEEE Transactions on Circuit Theory, 1973, 20(3): 203-211. [4]Moskowitz F. The Analysis of Redundancy Networks [J]. American Institute of Electrical Engineers, Part I: Transactions of the Communication and Electronics, 1958, 77(5): 627-632.[5]Hsu S J, Yuang M C. Efficient Computation of Terminal-pair Reliability Using Triangle Reduction in Network Management [C]//Proceedings of IEEE International Conference on Communications. Atlanta, 1998: 281-285.[6]Rocco S C M, Zio E. Solving Advanced Network Reliability Problems by Means of Cellular Automata and Monte Carlo Sampling [J]. Reliability Engineering & System Safety, 2005, 89(2): 219-226. [7]Billinton R, Allan N R. Reliability Evaluation of Engineering Systems, Concepts and Techniques[M].New York: Plenum Press,1992. [8]Fishman G S. A Comparison of Four Monte Carlo Methods for Estimating the Probability of s-t Connectedness [J]. IEEE Transactions on Reliability, 1986, 35(2):145-155. [9]Rocco S C M, Moreno J A. Network Reliability Assessment Using a Cellular Automata Approach [J]. Reliability Engineering & System Safety, 2002, 78(3): 289-295. [10]Zio E,Podofillini L,Zille V.A Combination of Monte Carlo Simulation and Cellular Automata for Computing the Availability of Complex Network Systems [J]. Reliability Engineering & System Safety,2006,91(2): 181-190. [11]Yeh W C, Lin Y, Chung Y Y. Performance Analysis of Cellular Automata Monte Carlo Simulation for Estimating Network Reliability [J]. Expert Systems with Applications, 2010, 37(5): 3537-3544. [12]Pozsgai P, Neher W, Bertsche B. Models to Consider Dependencies in Reliability Calculation for Systems Consisting of Mechanical Components[C]//Proceedings of Third International Conference on Mathematical Method in Reliability. Trondheim, 2002:1-4. [13]Goble M W, Brombacher C A, Bukowski V J.Using Stress-strain Simulations to Characterize Common Cause [M]. New York: Springer, 1998. [14]Roy D, Dasgupta T. A Discretizing Approach for Evaluating Reliability of Complex Systems under Stress-strength Model [J]. IEEE Transactions on Reliability, 2001, 50(2): 145-150. [15]周金宇, 谢里阳, 王学敏. 多状态系统共因失效分析及可靠性模型[J]. 机械工程学报, 2005,41(6): 66-70. Zhou Jinyu,Xie Liyang,Wang Xuemin.Analysis for Common Cause Failure and Reliability Model in Multi-state Systems[J]. Chinese Journal of Mechanical Engineering, 2005, 41(6):66-70. [16]Wang C N,Xing L D,Levitin G.Propagated Failure Analysis for Non-repairable Systems Considering both Global and Selective Effects[J].Reliability Engineering & System Safety,2012,99:96-104. [17]Xing L D,Wang C N,Levitin G.Competing Failure Analysis in Non-repairable Binary Systems Subject to Functional Dependence[J].Proceedings of the Institution of Mechanical Engineers,Part O:Journal of Risk and Reliability,2012,226(4):406-416. [18]Levitin G,Xing L D.Reliability and Performance of Multi-state Systems with Propagated Failures Having Selective Effect [J]. Reliability Engineering & System Safety,2010,95(6):655-661. [19]Xing L D,Dugan J B,Morrissette A B.Efficient Reliability Analysis of Systems with Functional Dependence Loops[J].Maintenance and Reliability,2009,43(3):65-69. [20]Levitin G,Xing L D,Hanoch B H,et al.Multi-state Systems with Selective Propagated Failures and Imperfect Individual and Group Protections[J].Reliability Engineering & System Safety,2011,96(12):1657-1666. [21]阮渊鹏,何桢.基于MCS-CA的考虑共因失效的复杂系统可靠性评估[J].系统工程与电子技术,2013,35(4):900-904. Ruan Yuanpeng,He Zhen.Reliability Evaluation of Complex Systems with Common Cause Failures Based on MCS-CA[J].Systems Engineering and Electronics,2013,35(4):900-904. [22]阮渊鹏,何桢,张旭涛,等.存在共因失效的复杂可修系统可靠性评估[J].中国机械工程,2014,25(10):1327-1324. Ruan Yuanpeng,He Zhen,Zhang Xutao,et al.Reliability Evaluation of Complex Repairable System with Common Cause Failures [J]. China Mechanical Engineering, 2014, 25(10):1327-1324. [23]阮渊鹏,何桢.基于MCS的多状态复杂系统可靠性评估[J].系统工程学报,2013,28(3):410-418. Ruan Yuanpeng,He Zhen.Reliability Evaluation of Multi-state Complex Systems Based on MCS[J].Journal of Systems Engineering,2013,28(3):410-418. (编辑袁兴玲) Reliability Evaluation of Complex System with Imperfect Protections Ruan YuanpengLi XiaoCui Jian Hangzhou Dianzi University,Hangzhou,310018 Because of the drawbacks of current researches when dealing with the problems of evaluating the reliability of a complex system containing components with propagated failures,a cellular automata-based Monte Carlo simulation algorithm was presented to deal with the complex problems,which combined the advantages of parallel computing of cellular automata and the flexibility of Monte Carlo simulation technology.The proposed algorithm considered the influences of imperfect protections on system reliability and overcame the limitations of system structure and the number of components. Finally, two given examples illustrated the validity of the proposed algorithm respectively and the method to analyze system reliability. complex system;propagated failure;imperfect protection;cellular automata;Monte Carlo simulation 2014-12-15 浙江省高校人文社科重点研究基金资助项目(ZD03-201401);浙江省自然科学基金资助项目(LQ14G010009,LQ13E050019) TB114.3;TH122< class="emphasis_italic">DOI :10.3969/j.issn.1004-132X.2015.22.004 阮渊鹏,男,1985年生。杭州电子科技大学管理学院讲师。主要研究方向为质量与可靠性工程。发表论文8篇。李晓,女,1977年生。杭州电子科技大学管理学院副教授。崔剑,女,1979年生。杭州电子科技大学管理学院副教授。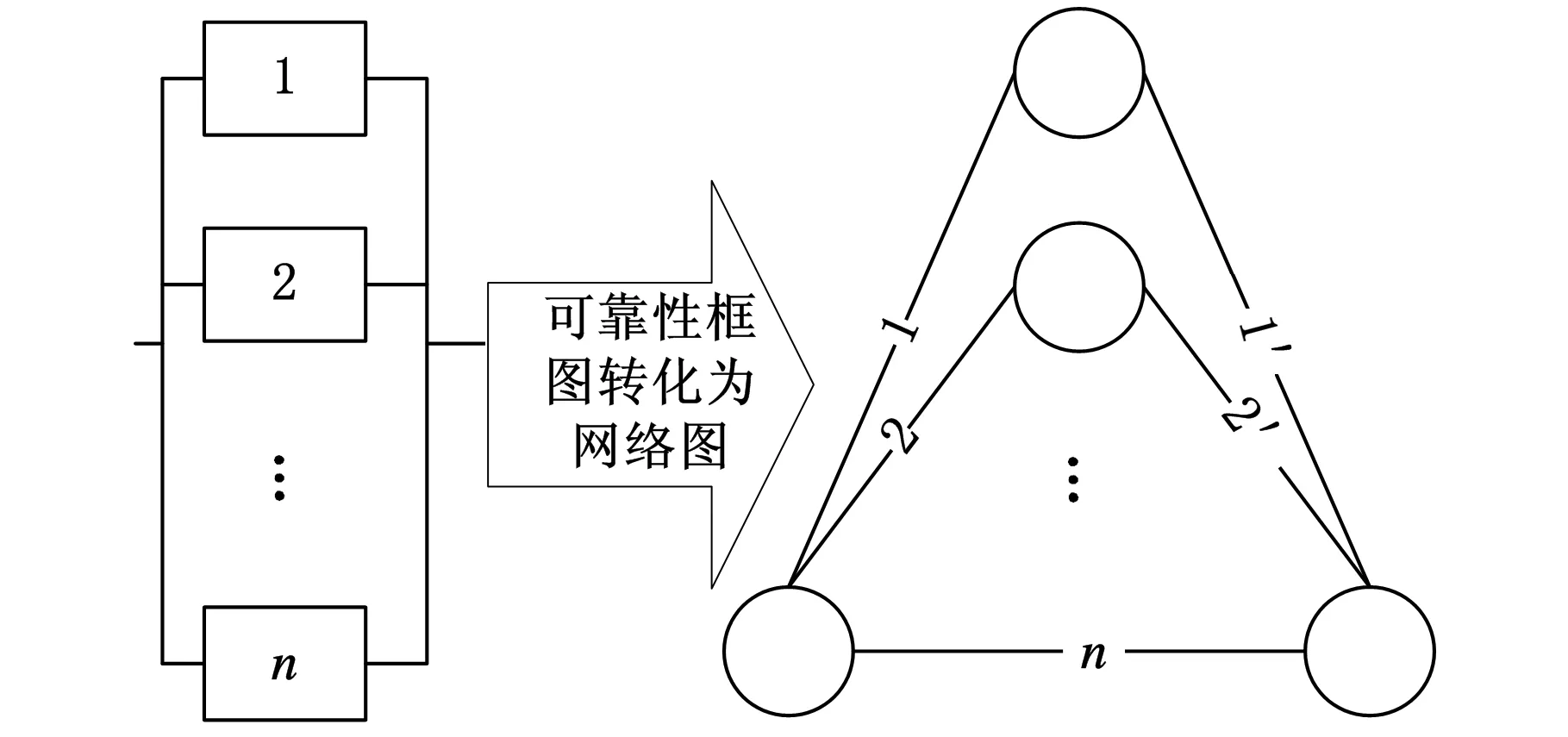
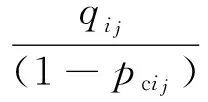
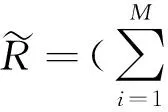

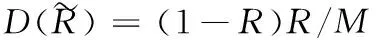
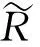
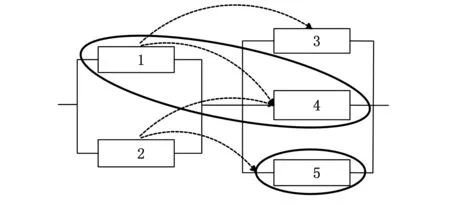
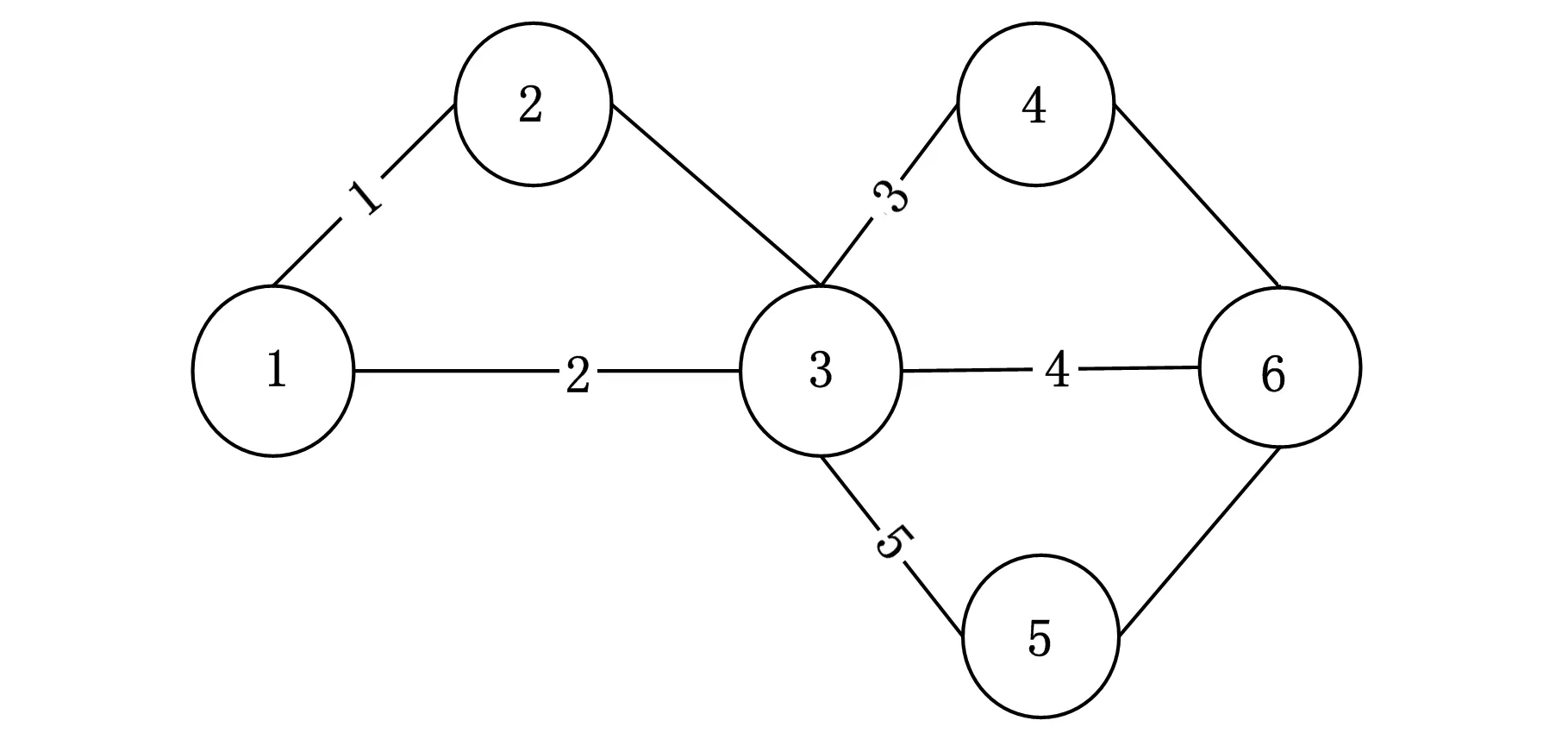
3 算例分析

4 结束语
