面向再设计的产品模块划分方法

周开俊　贡智兵　童一飞

1.南通职业大学，南通，226007　　2.南京康尼机电新技术有限公司，南京，2100133.南京理工大学，南京，210094

面向再设计的产品模块划分方法

周开俊1贡智兵2童一飞3

1.南通职业大学，南通，2260072.南京康尼机电新技术有限公司，南京，2100133.南京理工大学，南京，210094

针对现有模块划分方法的不足，提出和构建了产品模块划分的统一数学模型和求解流程。在此基础上，利用零件综合模糊相似矩阵构造了基于模块聚合度和分离度的适应度函数，同时根据模块划分矩阵的特点，应用矩阵交叉遗传算法进行了产品模块划分的优化求解。最后以某天文圆顶产品为例，说明了零件综合模糊相似矩阵的获取过程，以及算法的优化求解过程。实践证明该方法快速有效。

模块划分；相似矩阵；遗传算法；矩阵交叉

0　引言

产品的模块划分因影响产品最终的生产成本而备受研究人员和生产厂家的关注。通常情况下，产品的模块划分分为两个层次，一是产品创新设计之初，此时没有产品的物理原型，设计人员考虑客户需求和各功能单元之间的信息流、能量流及物料流的流动关系，在抽象层面进行的模块划分；二是已经有了产品物理原型，根据生产要求、维修保养要求及相关设计变更的要求，重新定义模块接口所进行的划分，此阶段属于实际操作层面的具体划分。如果说创新设计时，是体现客户需求兼顾生产制造要求的模块划分，那么产品再设计时的模块划分则是蕴涵客户需求，针对生产制造、装配、维修保养的具体要求进行的详细划分。

文献[1]面向广义工程更改，考虑企业生产更改、客户需求更改、供应商更改及环保需求更改等，采用模糊截取矩阵进行模块聚类；文献[2]面向产品配置，从模块组合复杂度、变形设计复杂度、配置成本等方面构建了模块优化模型，采用复合λ聚类方法进行模块划分；文献[3]面向产品设计，基于信息熵理论以模块产品设计中的横系列设计复杂度、纵系列设计复杂度和更新换代设计复杂度为优化目标，采用模糊树图法聚类进行模块划分方案优化；文献[4]基于公理设计、设计关联矩阵，采用关联距离聚类划分产品模块，并将实现产品族基本功能要求的模块定义为公用模块；文献[5]在模块聚类分析的基础上，从绿色产品的角度进行模块划分结果的优化；文献[6]面向产品全生命周期，针对每阶段的设计目标构造相关矩阵，由设计师对每一设计目标的模块划分结果进行对比和综合，得到最终的模块划分结果。综上所述，目前的模块划分方法[1-6]大都既考虑抽象层面的划分，又考虑操作层面上的详细划分，这就使得划分方法需要考虑的因素很多，模型过于复杂，划分算法通用性和实用性较差，难以应用和推广。

本文面向产品再设计，构建了产品模块划分的数学模型和统一求解流程，在此基础上根据数学模型的特点，应用矩阵交叉遗传算法进行产品模块划分的优化求解，实践证明该方法快速有效，具有较高的工程应用价值。

1　模型的建立及划分流程

1.1零件模块划分数学模型

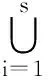
那么产品的模块划分可以用数学方法描述成如下形式：

(1)

现简记为

M=A•P

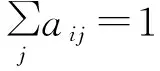
1.2零件的综合模糊相似矩阵

产品再设计时的模块划分，是根据现有产品物理结构，结合客户的多样化需求和功能独立性要求，以及产品装配、制造、维修等方面的实际情况进行的优化调整。因此，必须将这些影响产品模块划分的影响提取出来，建立零件之间的综合模糊相似矩阵：

R=[rij]n×n

(2)

c=max (wkrij,k)i≠j

其中，rij,k为各零件在客户需求、功能独立性、装配、制造、维修等因素上的相似度，从不同角度反映了客户的期盼、并行设计的要求、装配约束(如接触连接关系、序列规划的要求、装配稳定性的要求等)、制造特点(如配作、互为基准等)和维修保养的需要(如便于拆卸、易损件的更换等)等；wk为这些因素的影响权重。

1.3产品模块划分的统一流程

面向产品再设计的模块划分问题，其本质是基于零件综合模糊相似矩阵和相关关联条件，求解最优模块划分矩阵(式1)的问题，其求解流程如图1所示。设计人员可以根据具体情况，针对产品生命周期中一个或几个特定阶段提取初始信息，设置影响权重，获取不同划分方案，以保证模块划分方案的合理性和经济性。

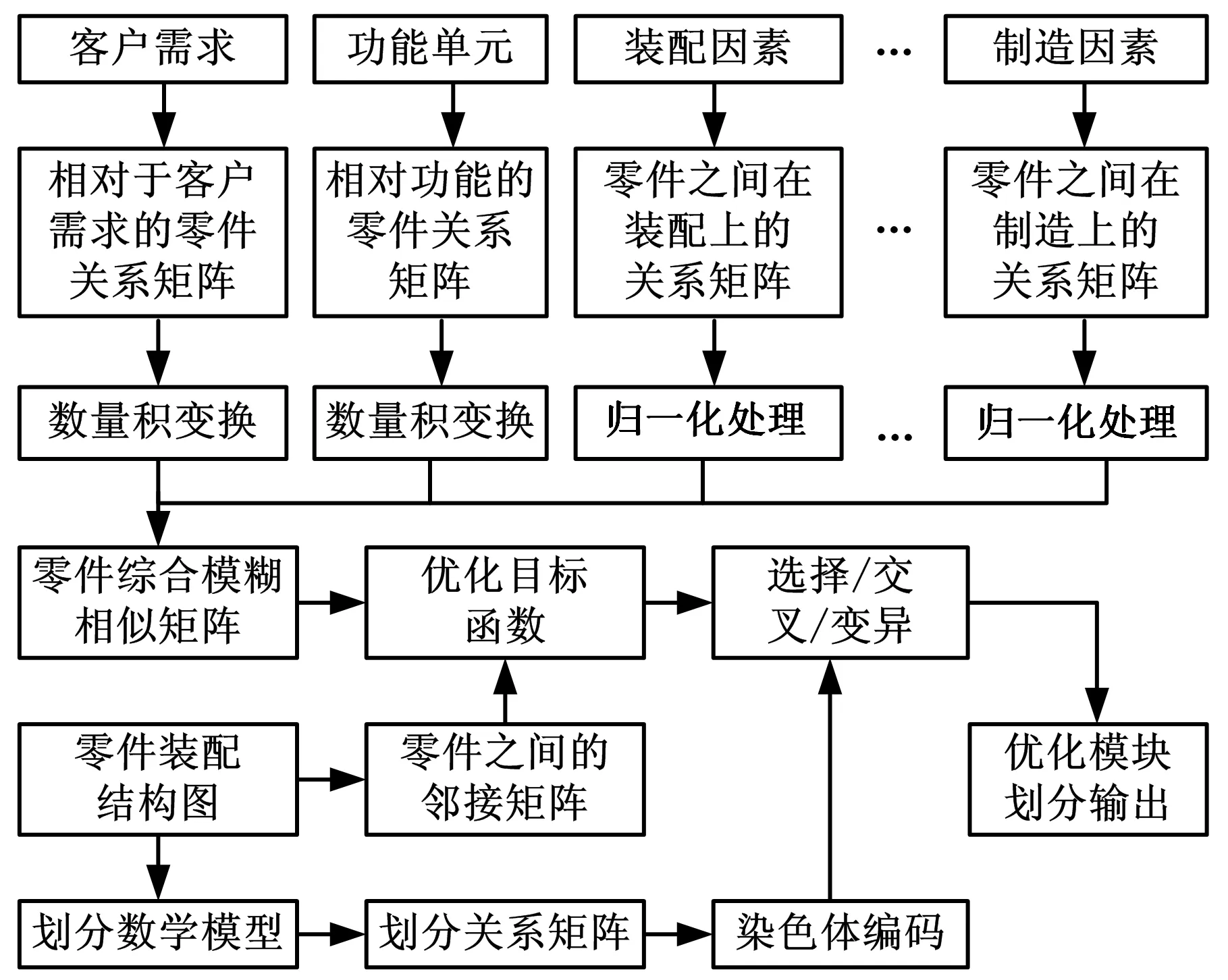
图1　面向产品再设计的模块划分求解流程

2　适应度函数的构造

为了评价模块划分的质量，需要构造一个适应度函数，用其来度量不同模块划分方案的优劣。借鉴文献[7]的思想，利用聚合度和分离度来构造模块划分的优化目标函数。假设产品P由n个关键零件组成，P={P1,P2,…,Pn}，P被划分成s个模块，M={M1,M2,…,Ms}，Mi与Mj为该划分的两个模块，其中Mi中有ki个零件，Mj中有kj个零件，则优化目标函数可构建为

(3)

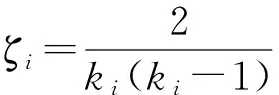
3　遗传算法操作

由于零件模块划分矩阵A=[aij]s×n只存在0和1两种元素，且每列只有一个1(即每个标号零件只属于一个模块)的特点，互换划分矩阵的列不仅可以改变模块的划分，而且不会违反式(1)的约束条件，因此零件模块划分矩阵非常适宜于整体作为遗传算法的基因编码。另外遗传算法是一种自适应全局优化概率搜索算法，对于一些大型、复杂的非线性系统，它更表现出了比传统优化方法更加独特和优越的性能[8]。由于其具有思想简单、易于实现、应用效果明显等优点而被众多应用领域所接受，因此本文选择应用遗传算法来优化求解零件模块划分矩阵。算法具体步骤如下。

(2)选择操作。选择操作是用来确定交叉重组的种群个体，本文采用轮盘赌的选择方法，在设定交叉概率Pc的条件下，随机选择交叉个体。

(3)交叉重组。为了保证种群的交叉效果，采用两点部分列交叉并移位重组方法。随机在两交叉的染色体中选择一个交配区域，如两父代染色体及交配区域选定为A、B，然后将B的交配区域加到A的前面，A交配区域加到B的前面，再顺次后移即得到两子代染色体A′和B′，具体过程如图2所示。这种方法的优点是无需考虑父代染色体情况，获得的子代均会有一定程度的变异效果，有利于保持种群的多样化。

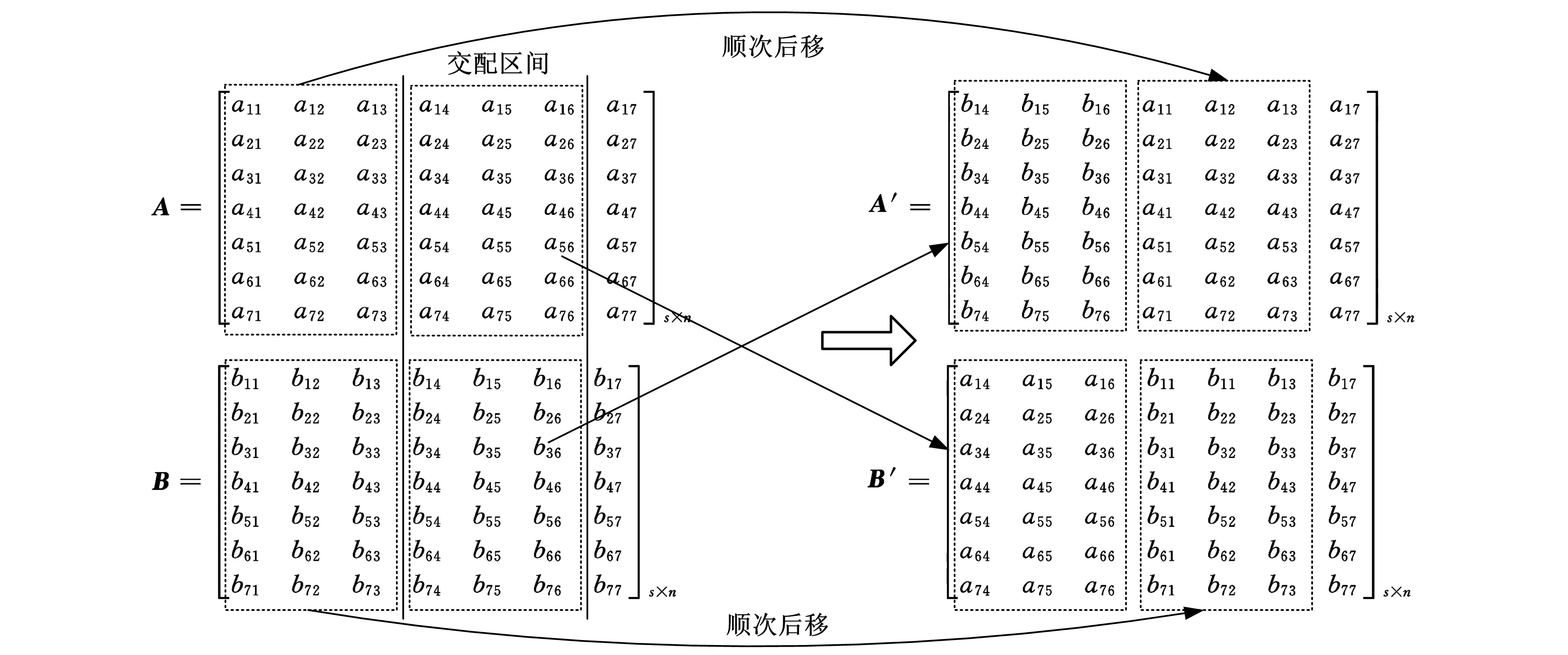
图2　两点部分列交叉并移位重组方法示意图

(4)变异技术。每代种群以设定的变异概率Pm进行变异，一旦发生变异，即随机产生两个互换列的位置，将染色体的对应两列进行互换。

4　应用实例分析

以天文观测中经常使用的天文圆顶产品为例，说明面向再设计的产品模块划分过程。图3为天文圆顶的结构图，该天文圆顶产品在实施观察或跟踪任务时，首先要打开天窗做好观察准备，同时在天文望远镜工作时会随着望远镜转动而同步转动。

表1为天文圆顶产品客户需求表，图4为天文圆顶产品功能结构图。本文综合考虑了客户需求、功能独立性、装配和制造四个因素，采用常用的5分制方法，根据表2获取原则分别获取相对于客户需求的关系矩阵X1=[xij,1]10×48、相对于功能独立性的关系矩阵X2=[xij,2]11×48，零件装配关系矩阵X3=[xij,3]48×48，零件制造关系矩阵X4=[xij,4]48×48。由图3、图4、表1知，零件数量为48，客户需求数为10，功能单元数为11。

对于X1=[xij,1]10×48和X2=[xij,2]11×48矩阵，采用数量积方法进行变换，分别获得零件相对于客户需求的相似度矩阵[rij,1]48×48和相对于功能独立性的相似度矩阵[rij,2]48×48。对于X3=[xij,3]48×48和X4=[xij,4]48×48，矩阵进行规一化处理，分别获得零件装配相似度矩阵[rij,3]48×48和零件制造相似度矩阵[rij,4]48×48，最后利用式(2)进行处理后获得零件综合模糊相似矩阵R=[rij]n×n，如表3所示。

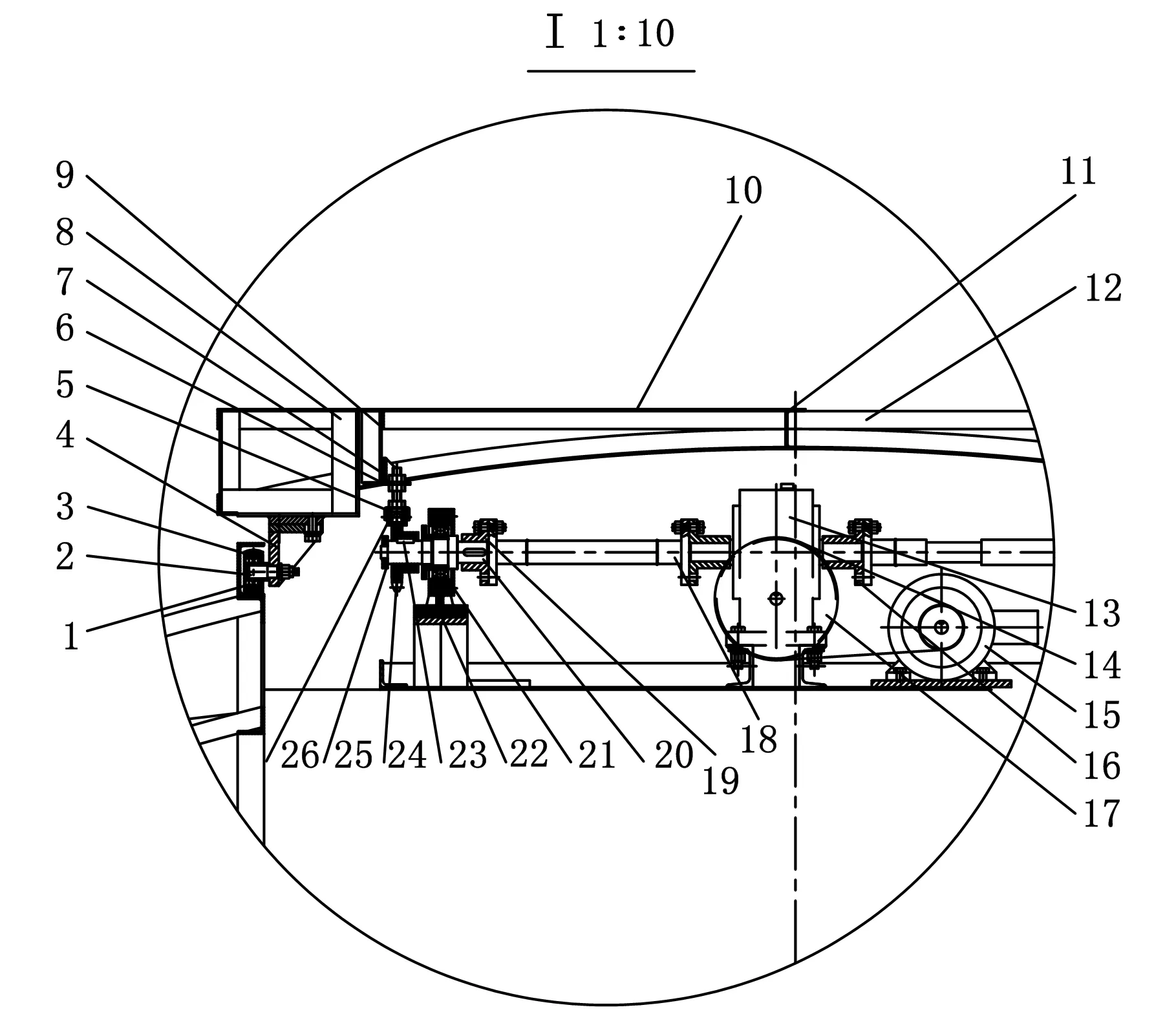
(a)局部视图Ⅰ

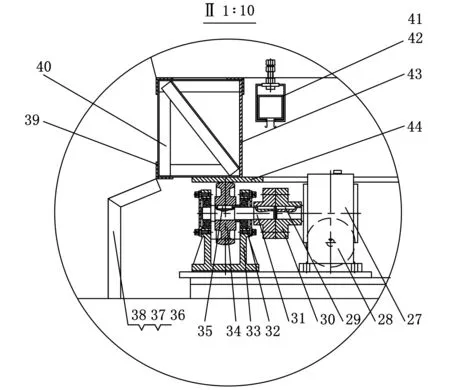
(b)局部视图2

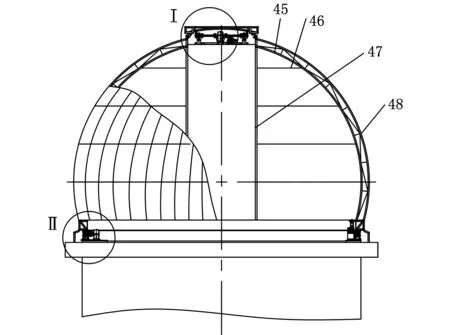
(c)主视图1.轴承1　2.轴承轴　3.滚轮　4.滚轮支架座　5.链条盒　6.内弧筋　7.螺杆架　8.天窗侧梁　9.外弧筋　10.天窗口门楣板　11.天窗蒙板　12.天窗截面梁　13.减速器　14.皮带　15.天窗电机　16.连轴节1　17.带轮　18.传递轴　19.连轴节2　20.传动轴　21.轴承2　22.轴承座　23.键1　24.链轮　25.防滑螺母　26.链条　27.减速器　28.圆顶电机　29.键2　30.连轴节3　31.轴　32.轴承3　33.轴承支架　34.摩擦轮　35.键3　36.裙边斜板　37.裙边直板　38.外圈筋　39.框架　40.底盘加强筋　41.导电环　42.挡块　43.站筋　44.底板　45.片梁4～14　46.环筋　47.导轨梁　48.内外蒙皮图3　天文圆顶结构图

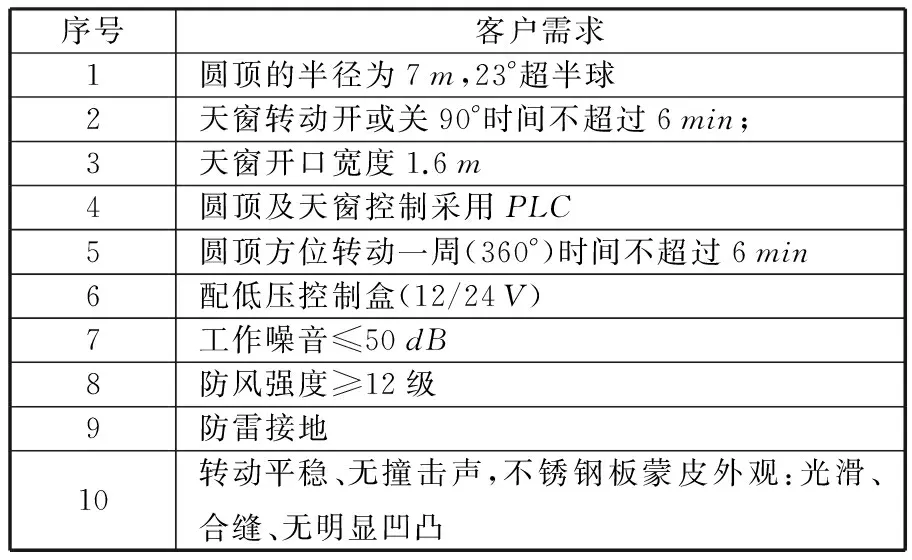
序号客户需求1圆顶的半径为7m,23°超半球2天窗转动开或关90°时间不超过6min;3天窗开口宽度1.6m4圆顶及天窗控制采用PLC5圆顶方位转动一周(360°)时间不超过6min6配低压控制盒(12/24V)7工作噪音≤50dB8防风强度≥12级9防雷接地10转动平稳、无撞击声,不锈钢板蒙皮外观:光滑、合缝、无明显凹凸

客户需求、功能独立性、装配和制造四个因素的权重，由技术人员打分，采用层次分析法[9]确定，考虑到本文是面向产品再设计或调整优化设计，因此弱化了客户需求和功能独立性的要求，突出了装配和制造等后期因素的影响，四个因素的影响权重分别为：w1=0.1，w2=0.2，w3=0.4，w4=0.3。

根据第3节所述的遗传算法操作方案，采用BorlandC++编写了算法原型程序。表4列出了在种群大小为100，交叉概率为0.8，变异概率为0.2时算法的迭代过程。实验结果表明该算法于349代收敛，获得最优模块划分结果为：(5,6,7,8,9,10,11,12,13,15,16),(18,19),(17,20,21),(22,23,24,25,26,27,28,29,30),(37,38,39,40),(41,42,43,44,45),(31,32,33,34,35,36,46,47,48),(1,2,3),(4,14)。该优化结果与工程实际情况基本吻合，说明本文提出的方法具有较好的普适性。

5　结语

产品的统一划分模型和求解流程揭示了零件模块划分的本质，设计人员可在产品生命周期的不同阶段有侧重点地提取初始信息和关联条件，构建优化求解函数，利用遗传算法求解零件划分矩阵。实践证明该方法快速有效，具有较高的工程应用价值。

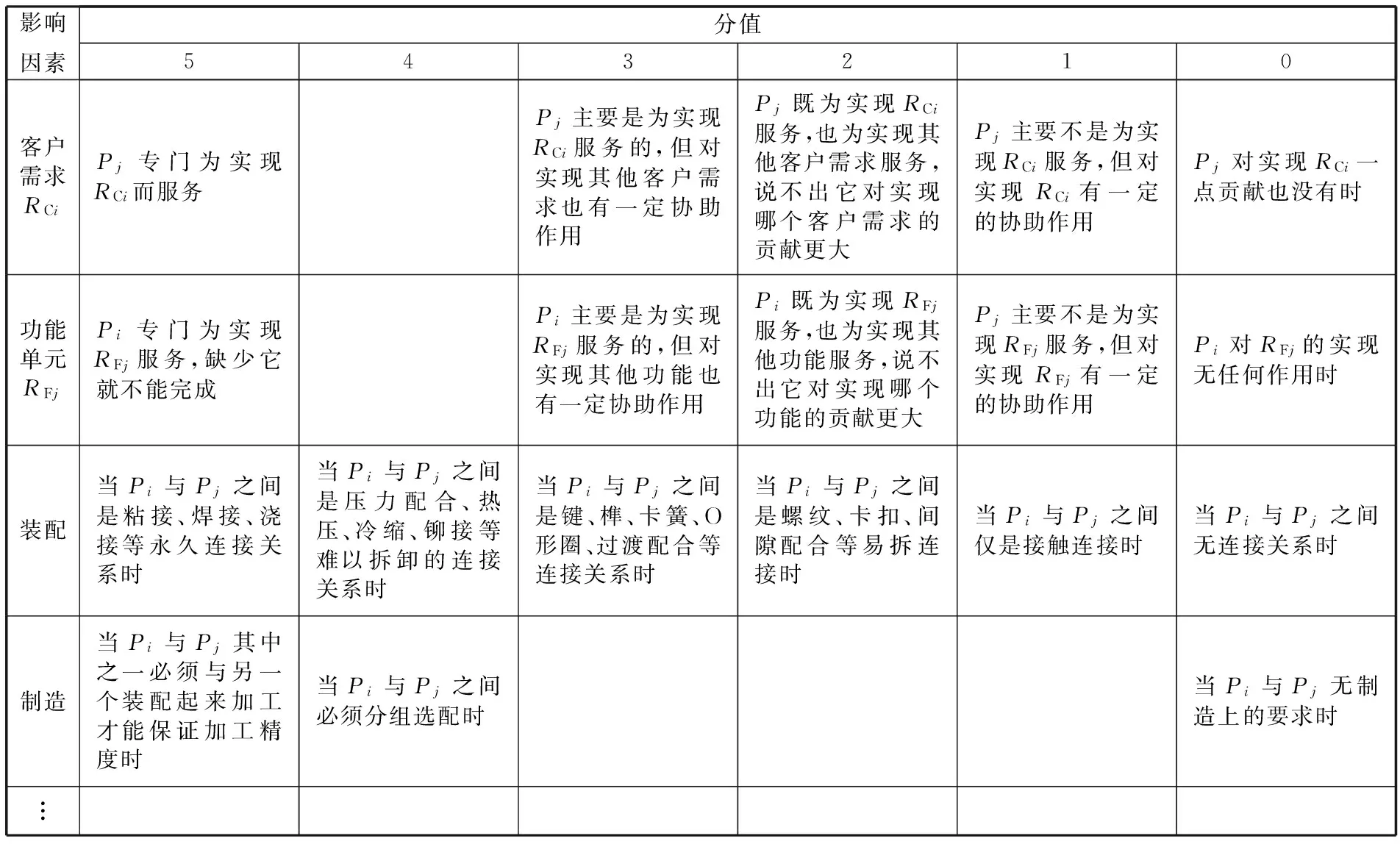
表2　四个影响因素对应的零件关系矩阵的获取原则

表3　零件综合模糊矩阵

续表3

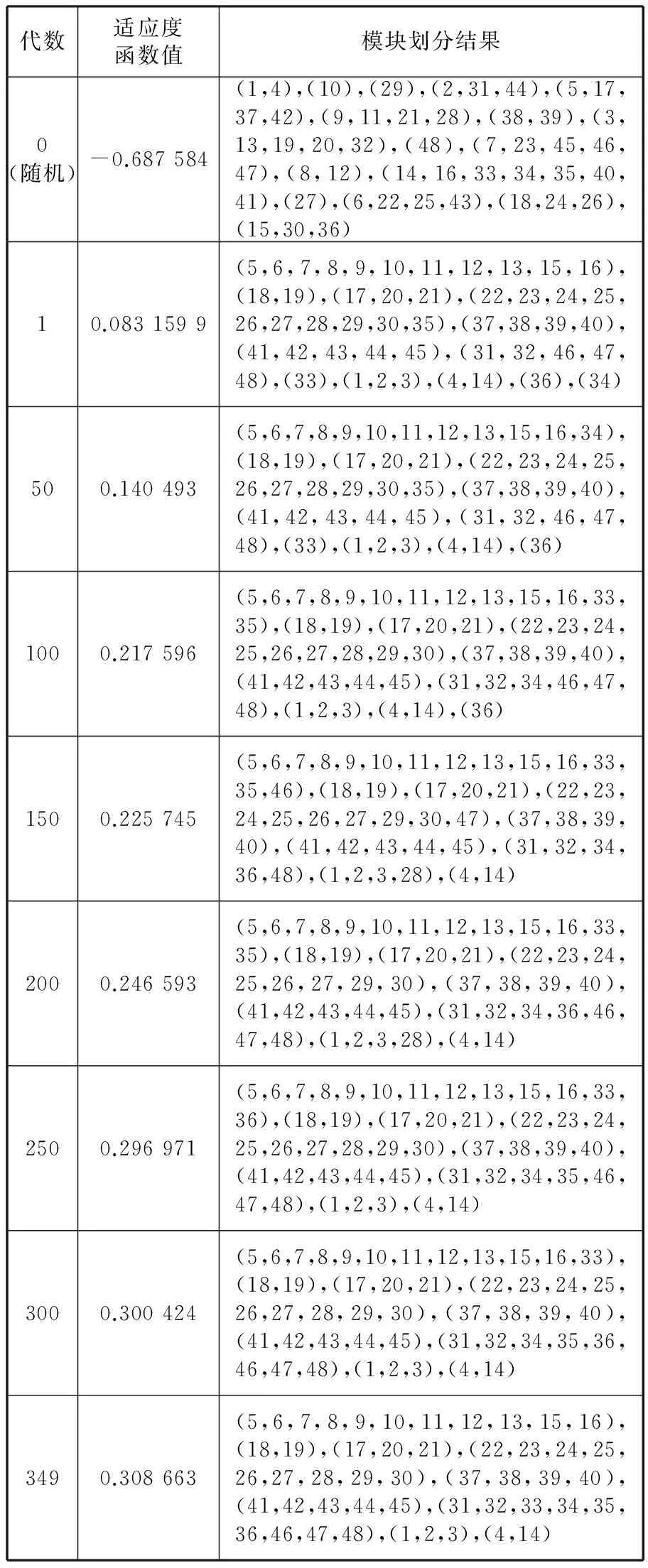
表4　天文圆顶模块划分优化结果

[1]章海峰，谭建荣，冯毅雄，等. 面向广义工程更改的产品模块划分方法研究[J]. 中国机械工程，2007，18(18)：2227-2232.

Zhang Haifeng, Tan Jianrong, Feng Yixong, et al. Research on Product’s Module Partition for Generalized Engineering Change[J]. China Mechanical Engineering, 2007，18(18)：2227-2232.

[2]贡智兵，李东波，史翔. 面向产品配置的模块形成及划分方法[J]. 机械工程学报，2007，43(11)：160-167.

Gong Zhibing, Li Dongbo, Shi Xiang. Module Generation and Module Partition Method for Product Configuration[J]. Journal of Mechanical Engineering, 2007, 43(11):160-167.

[3]王日君，张进生，葛培琪，等. 面向设计的产品模块划分方法[J]. 农业机械学报，2009，40(9)：182-186.

Wang Rijun, Zhang Jinsheng, Ge Peiqi, et al. Module Partition Method for Product Design[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(9)：182-186.

[4]肖人彬，程贤福，陈诚，等. 基于公理设计和设计关联矩阵的产品平台设计新方法[J]. 机械工程学报，2012，48(11)：94-101.

Xiao Renbin, Cheng Xianfu, Chen Cheng, et al. New Approach to Product Platform Design Based on Axiomatic Design and Design Relationship Matrix[J]. Journal of Mechanical Engineering, 2012，48(11)：94-101.

[5]Tseng H E, Chang C C, Li J D. Modular Design to Support Green Life-cycle Engineering[J]. Expert Systems with Applications, 2008, 34(5):2524-2537.

[6]Gu P, Sosale S. Product Modularization for Life Cycle Engineering[J]. Robotics and Computer Integrated Manufacturing, 1999, 15(5):387-401.

[7]周开俊，李东波，童一飞. 面向产品创新设计的功能模块划分方法[J]. 计算机辅助设计与图形学学报，2007，19(1)：73-77.

Zhou Kaijun, Li Dongbo, Tong Yifei. Function Module Partition Method for Product Innovative Design[J]. Journal of Computer-Aided Design & Computer Graphics, 2007，19(1)：73-77.

[8]邢文训，谢金星. 现代优化计算方法[M]. 北京：清华大学出版社，2001.

[9]闻邦椿. 机械设计手册：第6卷 现代设计理论与方法[M]. 5版. 北京：机械工业出版社，2004.

(编辑王艳丽)

A Module Partition Method for Product Redesign

Zhou Kaijun1Gong Zhibing2Tong Yifei3

1.Nantong Vocational University,Nantong,Jiangsu,226007 2.Nanjing Kangni New Technology of Mechantronic Co., Ltd.,Nanjing,210013 3.Nanjing University of Science and Technology,Nanjing,210094

In order to improve the defects in present methods of module partition, a unified product module partition mathematical model and solution processes were proposed. According to the characteristics of the mathematical model, a fitness function module was constructed based on the degree of polymerization and the degree of separation, then the matrix crossover genetic algorithm was applied for solving optimization module partition. Finally, taking astronomical dome products for example, the component integrated fuzzy similar matrix acquisition was illustrated, as well as the optimization algorithm for solving process. Practice has proved that this method is fast and effectives.

module partition; similar matrix; genetic algorithm; matrix-cross

2014-10-11

国家自然科学基金资助项目(61104171)；南通市科技计划资助项目(CP22013002)；江苏省青蓝工程资助项目(2014)

TP391< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.15.019

周开俊，男，1974年生。南通职业大学汽车与交通工程学院副教授、博士。主要研究方向为先进制造技术。获省级科技进步二等奖1项。发表论文20余篇。贡智兵，男，1980年生。南京康尼机电新技术有限公司技术中心研发部部长、工程师、博士。童一飞，男，1981年生。南京理工大学机械工程学院副研究员、博士。