飞机液压系统伺服舵机热力学分析与计算

李　晶　汤贵春　曹骏飞　是贤珠

1.同济大学,上海,201804 2.中国商用飞机有限责任公司上海飞机设计研究院,上海,201804

飞机液压系统伺服舵机热力学分析与计算

李晶1汤贵春1曹骏飞1是贤珠2

1.同济大学,上海,201804 2.中国商用飞机有限责任公司上海飞机设计研究院,上海,201804

为减少飞机液压系统故障,从温度控制层面对飞机液压伺服舵机进行热力学分析。将液压伺服舵机的物理模型简化为伺服阀控制作动筒的形式,建立液压伺服舵机热力学模型。根据热力学第一定律,采用集中参数法建立热力学方程。基于MATLAB平台，采用龙格-库塔法对舵机热力学模型进行编程仿真计算,得出舵机各节点温度分布曲线。将仿真结果与实验数据进行了对比,对比结果验证了飞机液压伺服舵机热力学模型的正确性,该模型可应用于飞机液压系统动态温度计算。

飞机;液压伺服舵机;热力学模型;仿真

0　引言

液压传动系统对工作介质的油温变化极其敏感,其工作稳定性很容易受温度变化影响。过高或过低的工作温度不仅会引起飞机液压系统的故障,甚至会造成灾难性的事故。相关研究资料表明,飞机发生故障的总数中液压系统的故障约占40%,在等级严重的事故中,约有15%～20%是由飞机液压系统故障引起的。因此,针对飞机液压系统进行热分析对其设计和元器件选型具有重要的指导意义。

舵机是飞机液压系统中十分重要的部件之一,其典型构成是一个伺服阀加作动筒。目前,针对飞机液压舵机的热力学模型研究很少。李永林等[1]、曹克强等[2]对液压伺服阀进行了热力学建模,在其伺服阀热分析模型中将伺服阀的供油控制体视为不变,此模型可用于计算伺服阀本身的发热,对于带动负载做往复运动的伺服舵机而言,该模型尚不能直接应用；王然然等[3]对气缸腔的热力学过程建立了较为准确的数学模型；谢三保等[4]对飞机液压系统温度仿真进行了研究,利用动态油温计算法建立了典型液压元件的温度模型；Li等[5]、李永林等[6]对柱塞泵进行了热力学建模。上述研究对液压元件的热力学模型的建立都有很大的参考意义。

本文针对飞机液压系统中的重要部件——液压伺服舵机进行热力学建模和分析,用MATLAB对其仿真计算,并进行实验验证,从温度控制层面为液压系统设计和元器件选型提供参考。

1　热力学基本原理

采用集中参数法对液压伺服舵机进行热分析,并作如下假设：①油液为一维流动；②控制体内油液性质均匀；③节流发热全部进入油液中；④忽略油液动能和势能的变化。取控制体如图1所示,根据热力学第一定律,有

(1)

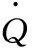
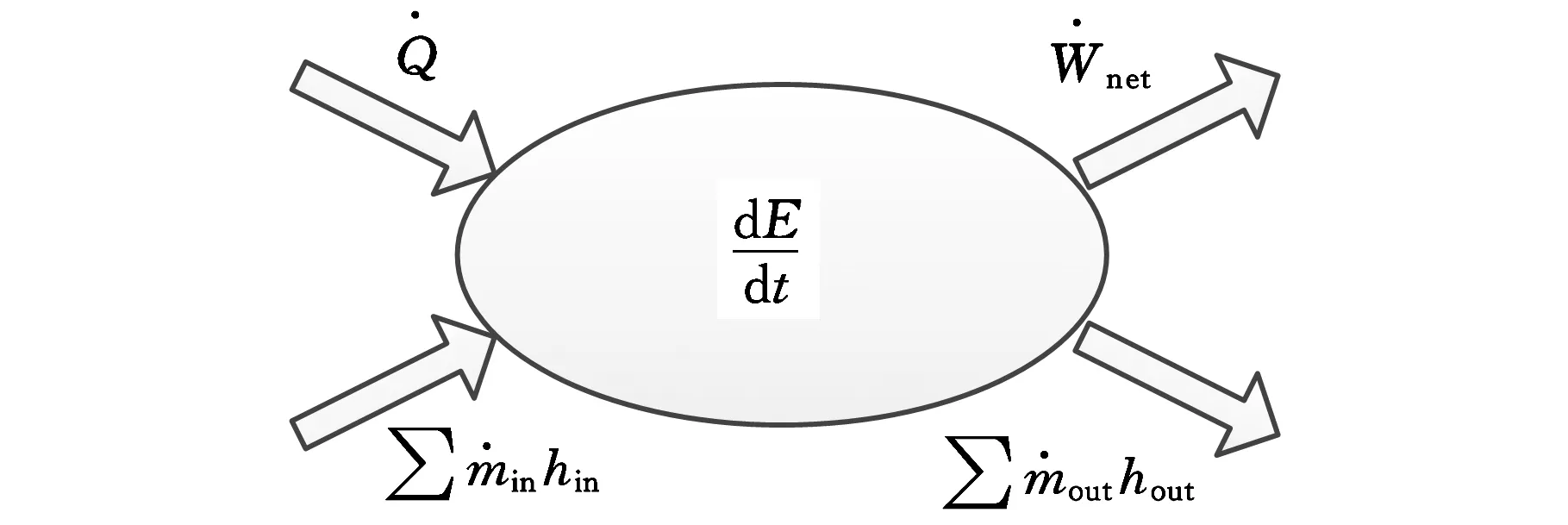
图1　控制体模型

在工程上,除了出口流速很大的喷管和进口流速很大的扩压管这两种特殊管道外,通常忽略控制体内部油液宏观动能与宏观位能的变化[7]。所以控制体内的储存能E的变化近似等于其热力学能U的变化,则有

(2)

式中，u为流体比内能；m为容腔内质量。

根据比焓(h)的定义及其微分形式，有

h=u+pν

(3)

(4)

式中，p为流体压力；ν为比体积；cp为流体定压比热容；T为流体温度；α为流体体积膨胀系数。

联立式(1)～式(4)，可得

(5)

其中,净功Wnet一般由轴功和边界功组成,本模型中轴功功率为零,故有

(6)

容腔内质量变化率为

(7)

一般情况下,可以近似认为流出控制体的油液温度与控制体内油液的平均温度相同,故可假设流出控制体的比焓与控制体内的平均比焓相同。由式(3)～式(7)可得

(8)

式中，Tin为流入控制体的油温；pin为控制体的进口压力。

2　液压伺服舵机系统热力学分析

2.1液压伺服舵机工作原理分析

飞机液压伺服舵机是一个高度复杂精密的机电液一体化传动控制机构,由电液伺服阀和作动筒两大部件组成。电液伺服阀精确控制进入作动筒的油液流量,实现飞行控制动作要求,其简化结构原理如图2所示。

图2　液压伺服舵机工作原理图

2.2伺服阀工作发热原理分析

伺服阀的工作原理如图3所示,在伺服滑阀换向时可实现液压伺服舵机的正反向运动。

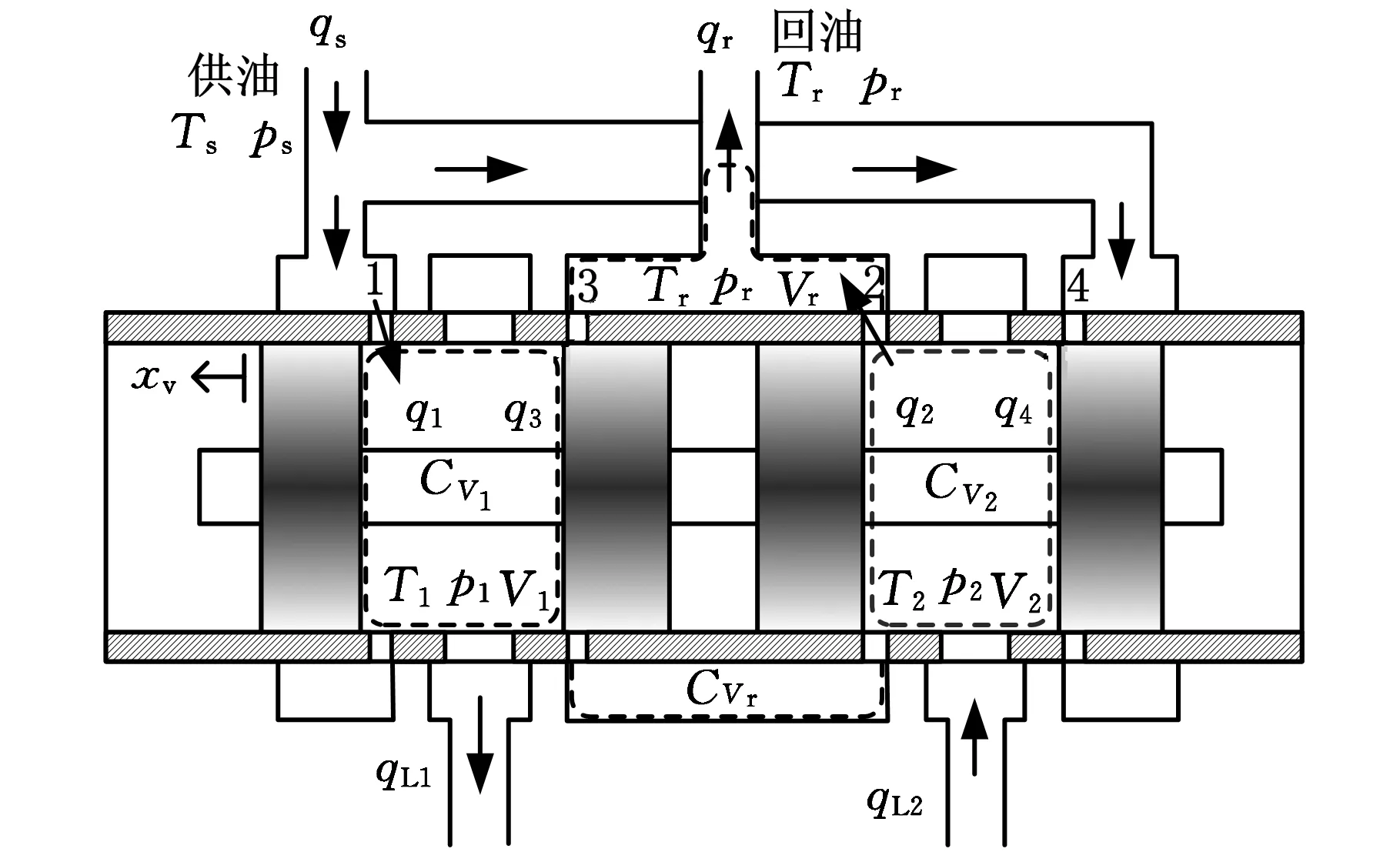
(a)阀芯左移

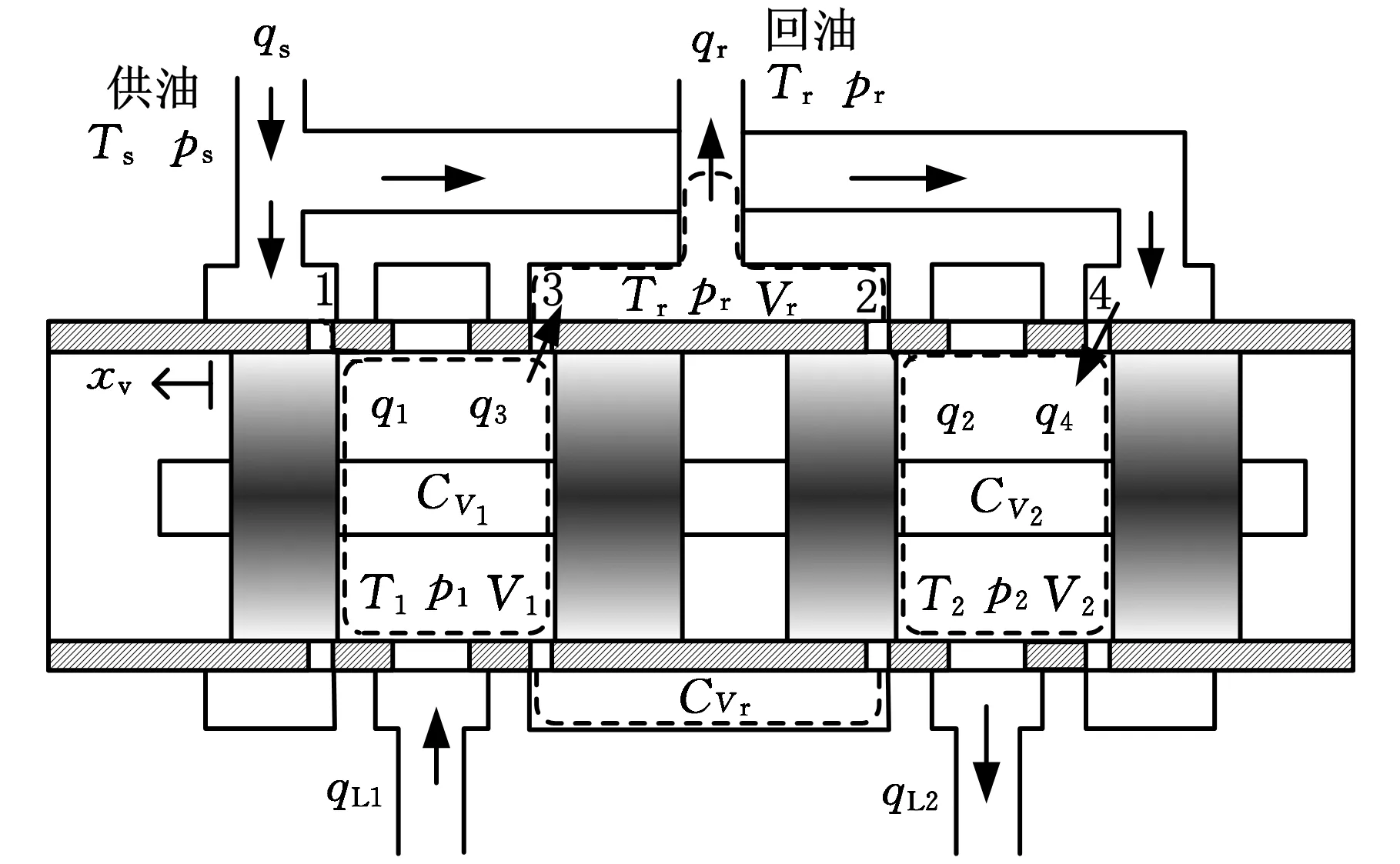
(b)阀芯右移图3　三位四通圆柱滑阀等效结构示意图

图3中阀内液压油被划分为CV1、CV2和CVr三个部分。xv为阀芯位移，当阀芯左移(xv>0)时,CV1为供油控制体；当阀芯右移(xv<0)时，CV2为供油控制体；CVr为回油控制体。阀的进口压力、流量和温度分别为ps、qs和Ts；回油压力、流量、温度和控制体CVr的体积分别为pr、qr、Tr和Vr；p1、T1和V1分别为控制体CV1的压力、温度和体积；p2、T2和V2分别为控制体CV2的压力、温度和体积。阀芯四个节流口处流量分别为q1、q2、q3、q4。阀出口与负载连接的两端的流量分别为qL1和qL2。其中，当油液流出阀体时qL1的符号为正,流入阀体时qL1的符号为负；当油液流入阀体时qL2的符号为正,流出阀体时qL2的符号为负。忽略液压油的压缩性,根据质量守恒定律可得

qs=q1+q4

(9)

qr=q2+q3

(10)

qL1=q1-q3

(11)

qL2=q2-q4

(12)

忽略阀和负载外泄漏流量，则有

qs=qr

(13)

qL1=qL2

(14)

由于先导阀的流量及其压差损失远小于负载的流量及其压差损失,故先导阀中控制油液产生的发热量可以忽略不计。根据伺服阀和作动筒的工作原理,可建立其运动微分方程和热平衡方程。

2.3作动筒工作发热原理分析

作动筒的工作简图见图4,图4中，T3、p3、V3分别为控制体CV3的温度、压力和体积，T4、p4、V4分别为控制体CV4的温度、压力和体积；pL为负载压强，q5为油缸的内泄漏流量,q6和q7为油缸的外泄漏流量。

图4　作动筒工作简图

由于舵机中外泄漏量极小,此处略去不计,作动筒与伺服阀通过短管道连接,忽略管道压降,有

(15)

(16)

pL=p3-p4

(17)

3　液压伺服舵机热分析模型

3.1伺服阀的热力学模型

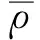
图5　伺服阀阀芯左移时热力学模型示意图

模型中各控制体对外做功功率为零,与壁节点、内部质量节点和上游流体节点的热交换相对于节流生热和油液流动带入的热量来说极其微小,对控制体节点温度影响甚微，且其中热力学参数确定较为复杂,常需通过大量试验结合经验公式才能确定。本文忽略滑阀控制体与外界的热交换，根据式(8)可得伺服阀热力学模型的微分方程组如下：

(18)

(19)

(20)

阀芯右移时模型结构类似,只需改变图5中qL1和qL2液流的方向,其回油腔温度计算公式不变,控制体CV1和CV2中温度变化相应改变为

(21)

(22)

3.2作动筒的热力学模型

作动筒的热力学模型会因为伺服阀阀芯位移方向和负载的不同而略有不同,在建模时需要分情况讨论。根据作动筒的简化物理模型,当伺服阀阀芯左移且负载pL向左时,作动筒的热力学模型如图6所示。图6中m3和h3为控制体CV3的质量和比焓；m4和h4为控制体CV4的质量和比焓；mw2和Tw2为作动筒质量节点的质量和温度；B3w2和B4w2分别为控制体CV3、CV4对作动筒壁节点的对流换热系数；B2为作动筒壁节点和外部空气的对流换热系数；TA为外部空气温度。

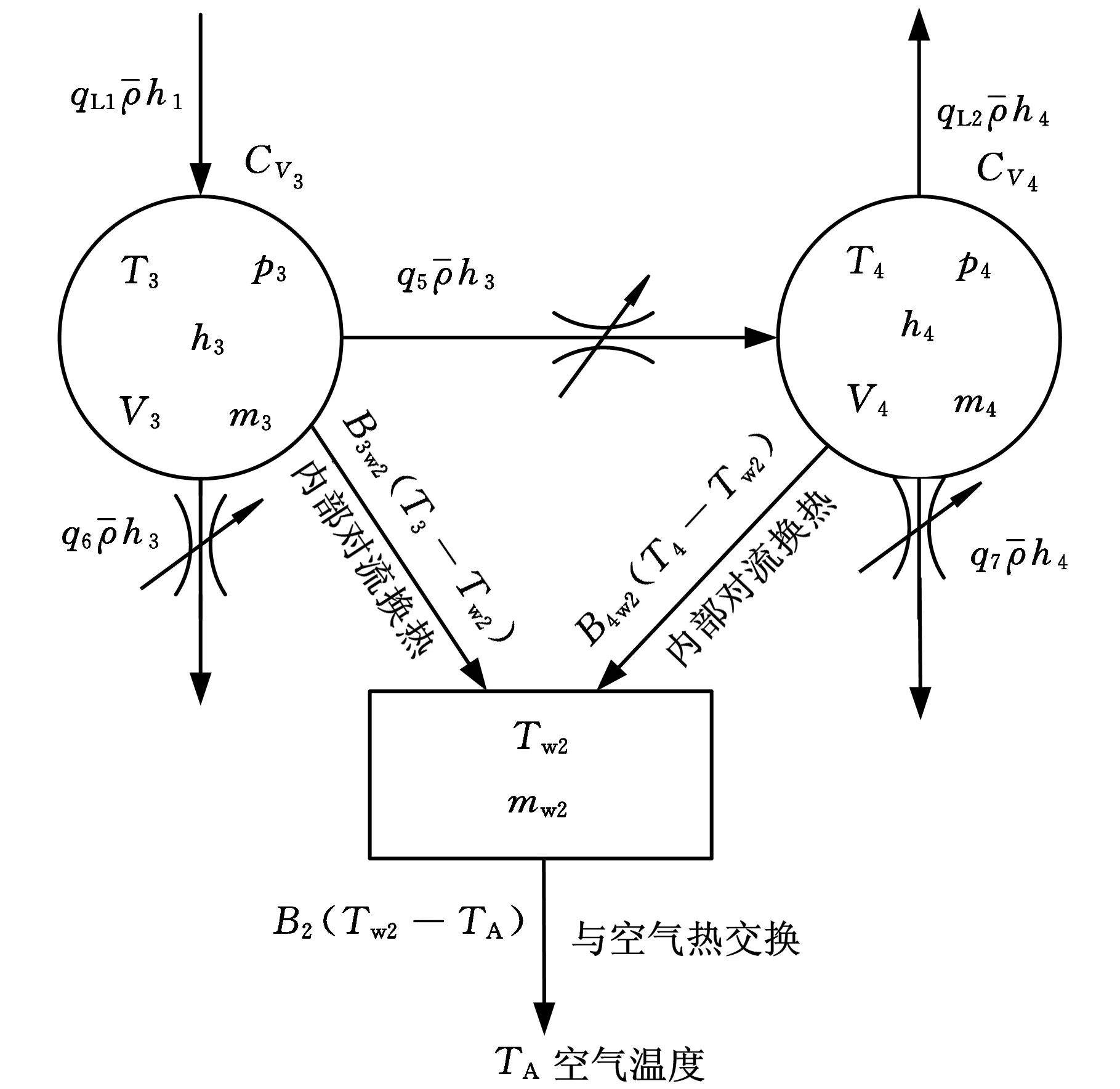
图6　伺服阀阀芯左移时作动筒热力学模型示意图

模型中各控制体对外部的轴功功率为零,作动筒内部流量泄漏较少,故自身发热量较少。其主要的热量来自于在液压油的流动过程中由工质自身的热量带入。金属壁与外部环境的热交换在一定程度上可以起到散热作用,因此在简化模型过程中考虑了其壁节点。通常作动筒的壁厚较薄,温差较小,本文假定壁节点各处的温度均相同。作动筒热力学模型的微分方程组为

(23)

(24)

B4w2(T4-Tw2)-B2(Tw2-TA)]

(25)

式中，cpw为金属外壁的质量热容；TA为外界空气温度；B3w2、B4w2和B2为相应的对流传热系数。

阀芯右移时模型结构类似,控制体CV3和CV4中温度变化热力学方程相应改变为

(26)

(27)

3.3液压伺服舵机热力学模型

液压伺服舵机可等效为伺服阀和作动筒的结合体,由伺服阀和作动筒各自的热力学模型,按照其相应的输入输出关系将其模型联立,得到舵机的热力学模型如图7所示。

4　算例分析

将上述推导的液压伺服舵机的热力学模型代入某型飞机舵机的具体参数进行仿真计算和分析如下[8-11]。

升降舵的负载和结构参数如表1所示。作动筒和伺服阀的参数根据某型号飞机参数确定,选取12号航空液压油。

表1　升降舵结构和负载参数

在MATLAB中采用龙格-库塔法对液压伺服舵机的热力学微分方程组编程求解，仿真步长为0.01 s，时间为80 s，并假设各控制体及油液的初始温度为293.15 K。

仿真结果如图8所示。由于作动筒负载与其位移近似成线性关系,故升降舵压力p1也与作动筒位移成线性关系。作动筒反复运动,则p1表现为周期性变化,如图8a所示。在30 s前各节点温度呈上升趋势,30 s后除壁节点外的各控制体节点的温度基本趋于平衡,都在各自的平衡温度附近上下振荡。

图8中值得注意的是控制体CV1、CV2的温度每个周期会出现两次波动。以控制体CV1为例,第一阶段的波动是由于控制体CV1为供油控制体,此时q1有较大的节流生热作用。随着压力p1的增大,节流压差是减小的,生热作用越来越弱,而流入的低温油有降温作用,油液温度开始下降。这时T3温度仍继续上升是由于p1压力升高的生热作用大于qL1流入的降温作用。

(a)控制体CV1、CV3温度曲线及CV1压力曲线

(b)控制体CV2、CV4、CVr及作动筒壁节点温度曲线图8　升降舵温度和压力曲线

在T1第二阶段的小波动期间控制体CV3因壁节点的对流换热温度开始降低,而控制体CV1则由于从CV3中流入的油液温度高于CV1的温度而开始升温,但CV3与CV1的温差越来越小。当带入的热量不足以抵消因压力p1的减小而损失的热量时,CV1的温度开始下降,这就造成了T1的第二次波动。

Tr的温度明显高于其他控制体的温度是因为回油控制体一直处于节流状态,发热量较大,约为控制体CV1和CV2的发热之和。Tr出现振荡是由于节流口2和节流口3的入口压力与回油压力pr之差在周期性地变化。虽然从仿真图上看到Tr的油液温度是波动的,但是相对于6.9K的温升来说其波动是十分微弱的,稳定后高低温温差小于1K,在实验中进行宏观上测量温度几乎是不变的。

某型飞机地面实验系统测试时,升降舵的入口与出口油液温差如表2所示。表2中，Ts、Tr及ΔT分别表示升降舵的进口油温、出口油温和进出口的油液温差。

表2　升降舵进出口油液温差　K

从表2中可以看出升降舵在前100 s温度上升较快，随测试时间的推移，升降舵的温度基本趋于稳定，进出口温差约为7.3 K。对地面实验测试的入口温度进行曲线拟合，并代入本文建立的舵机热分析模型中编程仿真。由表2中可知，由MATLAB编程求解的升降舵进出口温差约为6.9 K。对比两组数据可知本文建立的升降舵热力学模型仿真结果与某型飞机地面实验所得数据趋势一致,证明了模型的正确性。

5　结论

(1)根据热力学第一定律,采用集中参数建模的方法,建立了液压伺服舵机的热力学模型。

(2)以MATLAB为平台对伺服舵机热力学模型进行仿真计算和分析,并将仿真计算结果与实验数据进行对比,其一致性反映了该模型的正确性。

(3)本文提出的仿真计算模型在微小时间尺度内对液压伺服舵机内部工作节点的动态温度计算方法可以将细节变化都反映出来,这是实验环节难以做到的。该热分析模型可用于飞行器液压伺服舵机动态温度计算。

[1]李永林,李宝瑞,沈燕良,等.液压伺服阀的热力学模型研究及数字仿真[J]．系统仿真学报,2009,21(2)：340-347．

Li Yonglin, Li Baorui, Shen Yanliang,et al. Thermalhydraulic Modeling and Simulation of Hydraulic Servo Valve[J]. Journal of System Simulation,2009,21(2):340-347．[2]曹克强,李永林,任薄,等.现代飞机液压系统热特性建模仿真与热设计[M].北京:国防工业出版社,2013.

[3]王然然,李艾民,郑佳,等.气动伺服系统缸内热力过程研究[J].液压与气动,2014(3):13-16.

Wang Ranran, Li Aimin, Zheng Jia,et al. Thermodynamics Model of Pneumatic Cylinder Chamber[J]. Chinese Hydraulics & Pneumatics,2014(3):13-16.

[4]谢三保,焦宗夏.飞机液压系统温度仿真计算与分析[J]．机床与液压,2003,33(5):67-68．

Xie Sanbao, Jiao Zongxia. Temperature Simulating Calculation and Analysis of Aircraft Hydraulic System[J]. Machine Tool & Hydraulics,2003,33(5):67-68.

[5]Li Chenggong, Jiao Zongxia．Thermal Hydraulic Modeling and Simulation of Piston Pump[J]. Chinese Journal of Aeronautics,2006,19(4):354-358.

[6]李永林,徐浩军,曹克强,等. 航空柱塞泵全工况效率分析及热力学建模[J]. 北京航空航天大学学报,2010,36(12):1469-1472.

Li Yonglin, Xu Haojun, Cao Keqiang,et al. Efficiency Analysis and Thermal Hydraulic Modeling of Aerial Piston Pump at Whole Work Condition[J]. Journal of Beijing University of Aeronautics and Astronautics,2010,36(12):1469-1472.

[7]周继珠．工程热力学[M]．长沙:国防科技大学出版社,1999．

[8]A320 Aircraft Maintenance Manual[Z]. Airbus Industrie, 1997.

[9]B737-600/700/800/900AMM. D633A101-ILF[Z]. Boeing Company 1999～2005.

[10]B737-600/700/800/900 AMM. Part I Chapter 29[Z]. Hydraulic Power Boeing Company, 1999～2005.

[11]《飞机设计手册》总编委会.飞机设计手册(第12册)飞行控制系统和液压系统设计[M].1版.北京:航空工业出版社,2003.

(编辑王艳丽)

Thermodynamic Analysis and Calculation on Hydraulic Steering Units of Aircraft Hydraulic System

Li Jing1Tang Guichun1Cao Junfei1Shi Xianzhu2

1.Tongji University,Shanghai,201804 2.Chinese COMAC Shanghai Aircraft Design and Research Institute,Shanghai,201804

A thermodynamic analysis method was adopted to hydraulic servo steering units in temperature controlling for reducing aircraft hydraulic systems failure. A hydraulic servo steering units can be simplified to a servo valve and an actuator cylinder.Based on the first law of thermodynamics, the thermodynamic model of hydraulic steering units for aircraft was established. And the thermodynamic differential equations set of the model were derived with lumped parameter method, and solved by Runge-Kutta method. Simulations of hydraulic servo steering thermodynamics model were carried out by employing MATLAB software. And the calculation results coincide with the experimental data. The model presented herein can be used to calculate the dynamic temperature of aircraft hydraulic systems.

aircraft; hydraulic steering units; thermodynamic model; simulation

2014-09-12

国家自然科学基金资助项目(51275356)；工业和信息化部大型客机专项课题资助项目(MJF201302)

TH137< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.15.015

李晶,女,1972年生。同济大学机械与能源工程学院副教授。主要研究方向为液压系统及元件热分析、液压虚拟测试技术等。汤贵春,男,1990年生。同济大学机械与能源工程学院硕士研究生。曹骏飞,男,1990年生。同济大学机械与能源工程学院硕士研究生。是贤珠,女,1979年生。中国商用飞机有限责任公司上海飞机设计研究院工程师。