21-6-9高强不锈钢管数控弯曲回弹的理论计算及有限元分析

方　军　鲁世强　王克鲁　许小妹　徐建美　姚正军

1.南京航空航天大学，南京，211106　　2.南昌航空大学，南昌，330063

21-6-9高强不锈钢管数控弯曲回弹的理论计算及有限元分析

方军1,2鲁世强2王克鲁2许小妹2徐建美2姚正军1

1.南京航空航天大学，南京，2111062.南昌航空大学，南昌，330063

为了研究几何参数和材料参数对回弹的影响，基于弹塑性理论推导了最终弯曲半径和回弹角度的近似计算公式，结合有限元模拟，分析几何参数和材料参数对21-6-9高强不锈钢管材数控弯曲回弹规律的影响，并对理论解析、有限元模拟和试验结果进行对比。结果表明：最终弯曲半径随着弯曲半径、强度系数的增大或弹性模量、硬化指数的减小而增大，且与弯曲角度无关；回弹角度随着弯曲角度、相对弯曲半径、强度系数的增大或弹性模量、硬化指数的减小而增大；有限元模拟结果和试验结果吻合良好，能够较精确地预测回弹；理论解析与试验结果对比误差较大，但能够反映回弹角的变化趋势。

21-6-9高强不锈钢管；数控弯曲；回弹；理论解析；有限元分析

0　引言

21-6-9(0Cr21Ni6Mn9N)不锈钢管件具有高的强度、优良的抗腐蚀性能、良好的高温抗氧化性能，以及易达到产品轻量化等方面的要求，目前越来越多地应用于大型军用运输机和先进飞行器的液压管路系统、燃料或环境控制系统。管材数控弯曲成形技术能够满足管材弯曲成形过程高精度、高效率和低能耗的要求，从而实现管材塑性弯曲加工过程的高技术化，在航空航天等高科技领域中占有重要地位[1-4]，是实现高强不锈钢管等难变形材料精确弯曲成形的必然选择。然而，由于21-6-9不锈钢管具有高的屈服强度和弹性模量比，使得卸载回弹现象异常明显，严重影响其弯曲成形精度。管材数控弯曲成形是多模具约束和多因素耦合作用下的复杂非线性物理过程，成形因素难以控制。因此，研究21-6-9高强不锈钢管数控弯曲回弹规律，提高回弹的预测精度，从而实现回弹的有效控制及精确弯曲成形具有重要的工程意义和实用价值。

目前，国内外学者采用理论解析、试验研究和有限元数值模拟对管材弯曲回弹进行了大量的研究。Al-Qureshi等[5]基于平面应变假设，根据梁弯曲理论提出了预测弯管回弹和残余应力分布的理论公式，并应用于5052-O铝合金弯管的回弹预测。E等[6]基于纯弯曲理论和平面应变假设，推导出了回弹角和实际弯曲半径的计算公式，并结合有限元数值模拟和物理试验，研究了5A03铝合金和1Cr18Ni9Ti低强不锈钢管弯曲回弹行为。贾美慧等[7]以1Cr18Ni9Ti低强不锈钢管为研究对象，基于单向拉伸试验，提出并建立了符合不锈钢管材变形行为的分段本构模型，然后利用弹塑性变形理论构建了包括材料参数在内的管材弯曲回弹预测模型，揭示了各参数对回弹的影响规律。吴文云等[8-9]采用试验方法，研究了温度、弯曲速度、晶粒度和摩擦对镁合金管回转牵引弯曲成形回弹率的影响。Gu等[10-11]基于Dynaform平台建立了可靠的薄壁管数控弯曲、抽芯，以及回弹全过程弹塑性有限元模型,并采用该模型分析了低强不锈钢和铝合金薄壁管数控弯曲回弹行为。Jeong等[12]采用有限元法研究了成形条件对规格为φ1.5 mm×0.12 mm的镍铬铁合金625细管弯曲成形回弹的影响。Zhan等[13]利用数值模拟的方法研究了大直径薄壁CT20钛合金管的回弹机理及回弹补偿。Li等[14]采用塑性变形理论，显式/隐式三维有限元法和物理试验研究了高强Ti-3Al-2.5V钛管数控弯曲回弹特性和行为。Li等[15]采用显式和隐式有限元法，以中强薄壁6061-T4铝合金管为对象，研究了薄壁管回转牵引弯曲过程中几何依赖回弹行为。然而，有关21-6-9高强不锈钢管数控弯曲回弹的研究鲜有报道。为此，本文以规格为φ15.88 mm×0.84 mm(管径×壁厚)的21-6-9高强不锈钢管为研究对象，采用理论解析、有限元数值模拟研究了管材数控弯曲回弹行为，分析获得了几何参数和材料参数对管材数控弯曲回弹的影响规律，该研究可为高强不锈钢管等难变形材料回弹预测提供指导。

1　管材数控弯曲回弹分析

1.1单向拉伸试验

精确预测和定量分析回弹现象依赖于可靠准确的材料力学性能参数，包括应力应变曲线、硬化准则等。拉伸试验是了解材料力学性能和变化规律的最基本试验，通过单向拉伸试验可以获得材料的抗拉强度、延伸率、屈服强度、弹性模量等参数，而这些参数是影响管材弯曲成形质量的重要因素。在以往的管材弯曲研究中，大多数采用板材或棒材的力学性能参数，但由于管材制备过程需要热挤、冷拔、退火和矫形等工序，使得管材的力学性能已经发生了较大变化。为此，本文以21-6-9高强不锈钢管材为对象进行单向拉伸试验，获取其材料力学性能参数及构建本构模型，为有限元数值模拟提供准确可靠的材料力学性能参数。

根据国标GB/T228-2002设计管段拉伸试样。单向拉伸试验在万能电子试验机上进行，并将应力-应变曲线示于图1中。从图1可以看出，21-6-9高强不锈钢管在弹性变形阶段，严格遵守线性变形规律，到达屈服点之后没有明显的屈服平台，进入塑性变形阶段发生的是连续屈服变形并有明显的材料硬化特征。表1所示为21-6-9高强不锈钢管的材料力学性能参数。从表1可以看出，管材屈服强度和抗拉强度大，延伸率较小，管材变形所需要的变形力较大，但之后材料均匀塑性变形所允许的应力变化空间较小，不易于弯曲成形。同时，对于屈服强度与弹性模量之比值，21-6-9高强不锈钢管为0.51，大于1Cr18Ni9Ti低强不锈钢管的0.11和5052-O铝合金管的0.16[14]，因此，成形之后的卸载回弹很大。

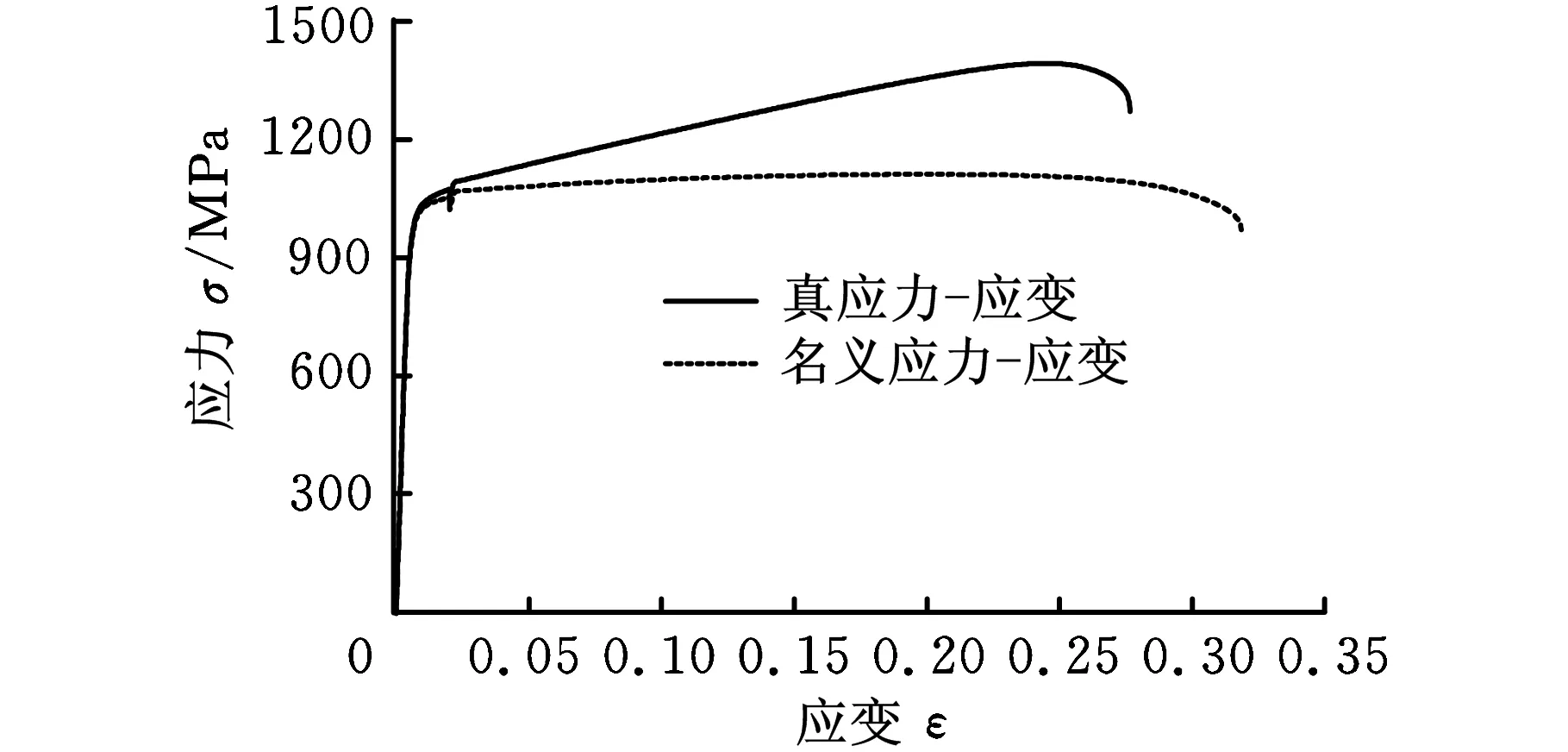
图1　21-6-9管材应力-应变曲线

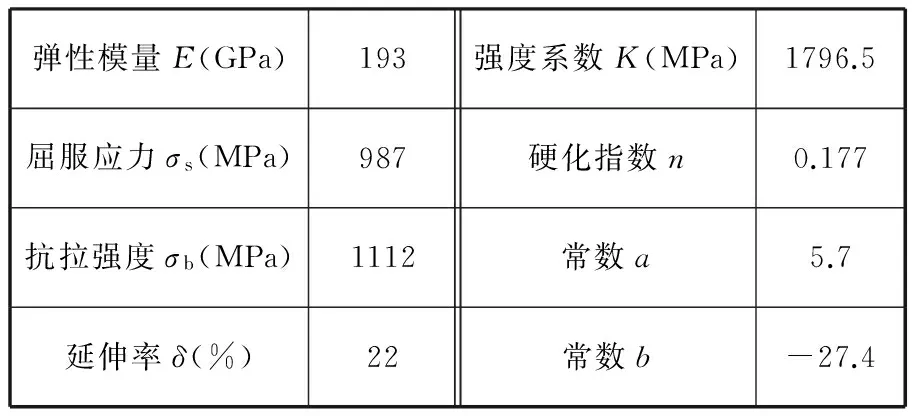
弹性模量E(GPa)193强度系数K(MPa)1796.5屈服应力σs(MPa)987硬化指数n0.177抗拉强度σb(MPa)1112常数a5.7延伸率δ(%)22常数b-27.4

采用Ludwigson方程σ=K εn+e(a+b ε)描述21-6-9高强不锈钢管的加工硬化行为[16]。对21-6-9高强不锈钢管单向拉伸试验数据进行拟合，其中拟合试验数据选自屈服点到抗拉强度极限之间，其拟合相似度为0.9994。图2所示为21-6-9高强不锈钢管屈服以后的应力-应变及拟合曲线，从图中可以看出，两条曲线的重合度很高，说明所得到的材料性能参数是稳定可靠的。

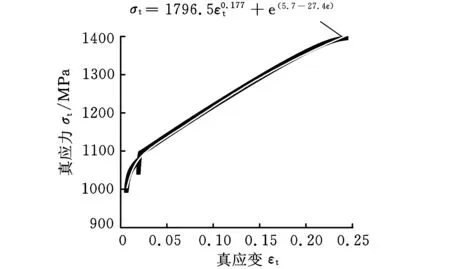
图2　21-6-9管材屈服以后的真应力-应变及拟合曲线

1.2管材数控弯曲回弹的理论分析

图3　管材弯曲变形过程切向变形的加载及卸载路径

塑性弯曲变形在加载中满足塑性应力应变关系，而在卸载回弹时满足弹性应力应变关系。假设管材弯曲时外侧壁材料受到弯曲切线方向的单向拉伸变形，则弯曲及回弹过程中的应力应变路如图3所示。管材弯曲沿OAC曲线加载至C点，弯曲成形后卸载至E点(忽略因非线性卸载等滞留的残余应变)，那么OE即为管材弯曲卸载回弹后外侧外表面纤维的实际变形量。为简化分析，假设回弹过程属于完全弹性变形，即OA∥EC，则Rt△OAB∽Rt△ECD,所以ED/OB=CD/AB。ED表示管材卸载回弹时外侧外表面纤维的弹性恢复量Δεθ，OB表示管材弹性弯曲阶段中与屈服应力σs相对应的切向应变εs，AB和CD分别表示管材弯曲成形加载过程中的屈服应力σs和卸载前的切向应力σθ。所以有

(1)

考虑到σs=E εs，则

Δεθ=σθ/E

(2)

假设弯曲过程中不考虑管材壁厚变化，则管材外侧外表面的平均切向拉应变为

(3)

式中，R为弯管中性层弯曲半径;D为管材原始直径。

卸载回弹后弯管外侧外表面的实际切向拉应变为

(4)

式中，R′为弯管卸载回弹后的中性层曲率半径。

又有

(5)

将式(2)、式(3)和式(4)代入式(5)中，整理后得

(6)

管材弯曲卸载后的回弹角Δθ满足：

Δθ=θ-θ′

(7)

式中，θ为弯曲角;θ′为弯曲卸载后的实际成形角。

假设管材弯曲前后中性层保持不变，则

R θ=R′θ′

(8)

将式(6)和(8)代入式(7)，并整理得

(9)

将21-6-9高强不锈钢管的加工硬化模型代入式(9)，得到其回弹角度的计算公式

(10)

1.3管材数控弯曲回弹的有限元分析

基于ABAQUS软件平台，建立了21-6-9高强不锈钢管数控弯曲三维有限元模型，如图4所示。精确预测回弹依赖于每一个成形步中获得准确可靠的应力应变分布，因此，显示算法用于求解管材弯曲和抽芯过程，隐式算法用于求解回弹过程，即采用ABAQUS/explicit进行弯曲和抽芯模拟，然后把弯曲抽芯后的结果直接导入ABAQUS/standard进行卸载回弹分析。在回弹分析时包含几何非线性的影响，并采用阻尼因子来稳定隐式迭代步以利于快速获得回弹分析结果。

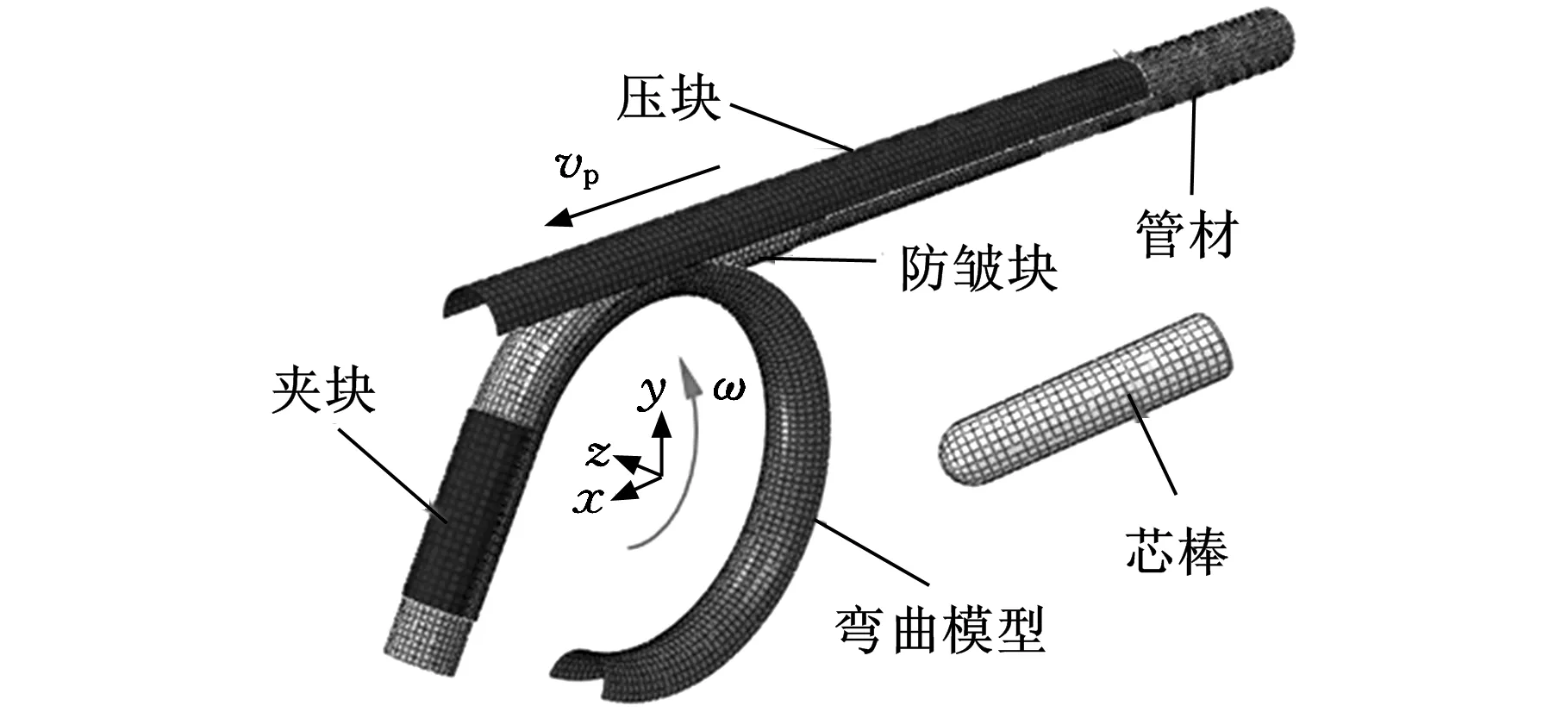
图4　21-6-9高强不锈钢管数控弯曲三维有限元模型

采用4节点四边形壳单元S4R来描述管材，厚度方向选取5个积分点；采用离散刚性壳单元R3D4来描述刚性模具(弯曲模、压块、夹块、防皱块和芯棒)对管材施加力的接触几何曲面。选取弹塑性本构模型来描述管材特性，Ludwigson方程表征加工硬化特征。选用经典的库仑摩擦模型来描述管材/模具之间接触情况。采用1.5 mm×1.5 mm和2 mm×2 mm网格分别来离散管材和模具表面。在弯曲模拟过程中，为了保证计算精度和效率，质量放大因子选用2000。弯曲过程中采用双精度进行计算，卸载回弹采用单精度进行计算。

采用面-面接触对算法；采用位移/转动和速度/角速度两种方法来施加边界约束。弯曲模和夹块采用相同的约束，仅开放绕z轴的转动自由度；压块仅开放沿x轴方向的平动自由度；防皱块的所有自由度在弯曲过程中被约束；芯棒在弯曲过程中各个自由度为零，在完成设定的角度后回撤，开放沿x轴方向的平动自由度。采用光滑幅值曲线定义模具的加载过程以减小惯性效应的影响。卸载过程所用的模具被移除，并采用固定边界约束来避免刚体运动，如图5所示。

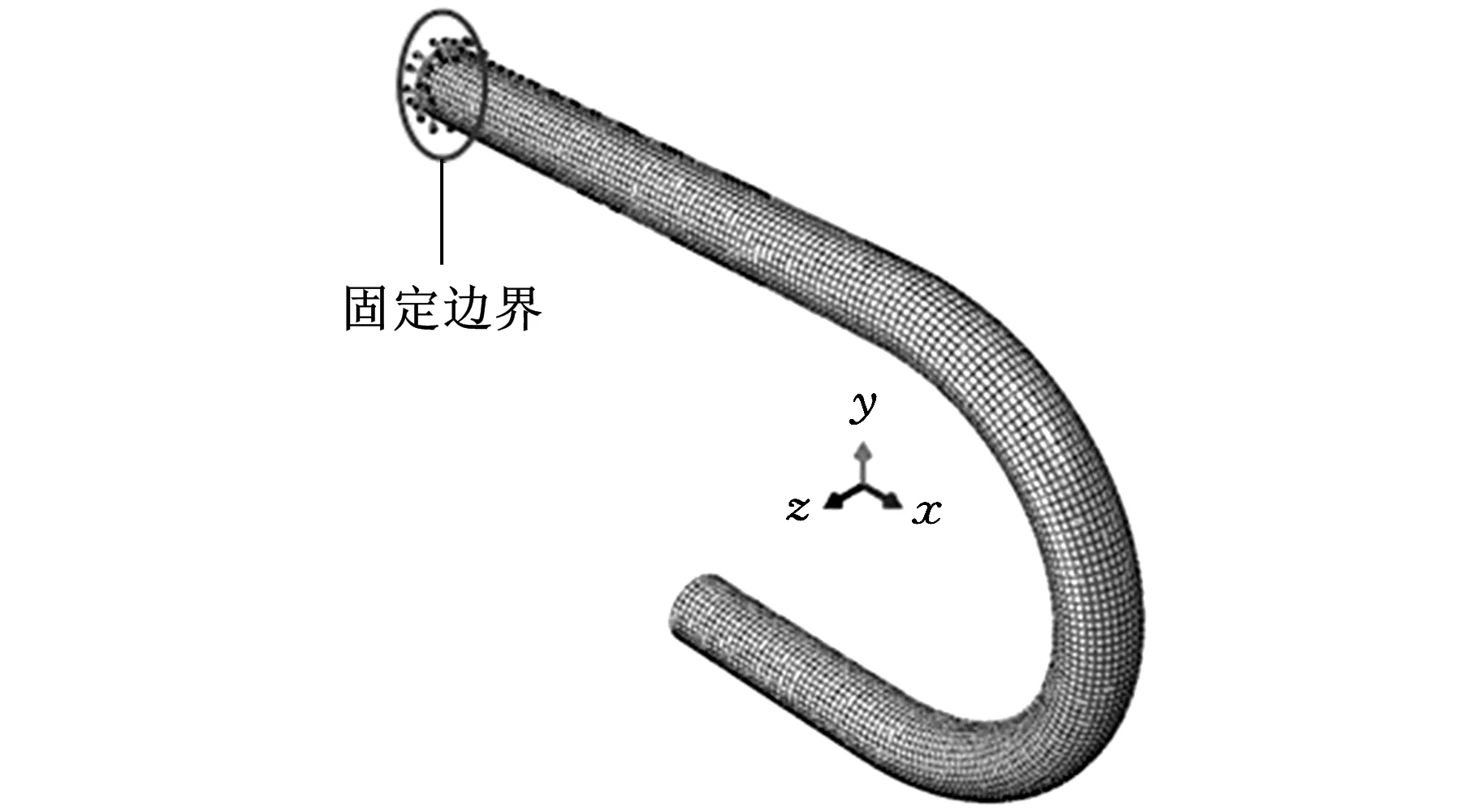
图5　回弹模型的约束条件

2　结果及讨论

为了获得21-6-9高强不锈钢管材数控弯曲回弹规律，基于式(10)选取对回弹角有影响的因素，采用解析和模拟的方法研究了几何参数(弯曲角度θ，相对弯曲半径R/D)和材料参数(强度系数K、硬化指数n和弹性模量E)对21-6-9高强不锈钢管材数控弯曲回弹角的影响规律。

2.1几何参数对回弹角的影响

图6所示为几何参数对21-6-9高强不锈钢管数控弯曲回弹的影响。从图6a可以看出，回弹角的解析值和模拟值均随着弯曲角度的增大而基本呈线性增大，这是因为在其他条件一定的情况下，随着弯曲角度的增大，参与管材弯曲塑性变形的材料增多，累积的弹性变形量也随之增大，卸载后弹性回复增大，宏观表现为卸载后回弹角越大。从图6a还可以看出，回弹角的解析值随弯曲角的增大，线性增大的趋势较模拟值大，这可能是因为在进行回弹理论公式推导时进行了大量的假设，并且没有考虑管模的实际接触条件对弯曲成形的影响，使回弹解析值随弯曲角度的增大线性增大的趋势更大。

图6b所示为相对弯曲半径对回弹角的影响，由图可以看出，随着相对弯曲半径的增大，回弹角的解析值和模拟值逐渐增大，且弯曲角度越大，回弹角增加的趋势越大。这是因为，在管径相同的前提下，弯曲半径的大小表示管材弯曲成形变形程度的大小，弯曲半径越大，管材弯曲变形程度越小，管材中处于弹性变形状态的区域越大，因此卸载时弹性成分引起的弹性回复越大，表现为回弹角的增大。

(a)弯曲角度的影响

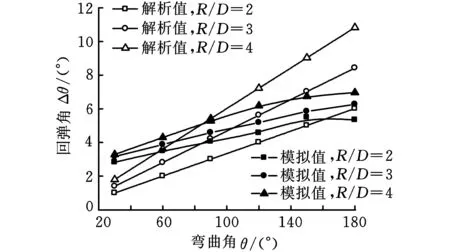
(b)相对弯曲半径的影响图6　几何参数对回弹角的影响

2.2材料参数对回弹角的影响

图7所示为材料参数对21-6-9高强不锈钢管数控弯曲回弹的影响。从图7a可以看出，回弹角的解析值和模拟值均随着强度系数K的增大而显著增大，且弯曲角度越大，回弹角增大的趋势越大。这是由于强度系数越大，同等应变情况下对应的应力值越大，在相同的弹性模量下，同样应变中的弹性应变越大，卸载产生的回弹角越大。弯曲角度越大，回弹角随强度系数增大的趋势越大，这是由于弯曲角度和强度系数耦合影响的结果[17]。

图7b所示为硬化指数对回弹角的影响，从图中可以看出，回弹角的解析值和模拟值均随着硬化指数n的增大而减小。这是由于在应变小于1时，硬化指数越大，同样应变情况下对应的应力值越小，在弹性模量相同的情况下，同样应变的中的弹性应变越小，表现为卸载回弹角越小。从图7b还可以看出，不同硬化指数对回弹模拟值的影响较小，对回弹解析值的影响较大，这可能同样是由于在回弹理论公式推导时进行了大量假设，且没有考虑管模实际接触条件等对回弹的影响，使得硬化指数对回弹解析值的影响偏大。

图7c所示为弹性模量对回弹角的影响，从图中可以看出，回弹角的解析值和模拟值均随着弹性模量E的增大而减小，且随着弯曲角度的增大，回弹角的减小趋势增大。这是由于弹性模量越大，同样应变中的弹性应变成分越小，导致回弹角度减小。弯曲角度越大，回弹角随弹性模量的增加而减小的趋势越大，这同样是由于弯曲角度和弹性模量耦合作用的结果[17]。

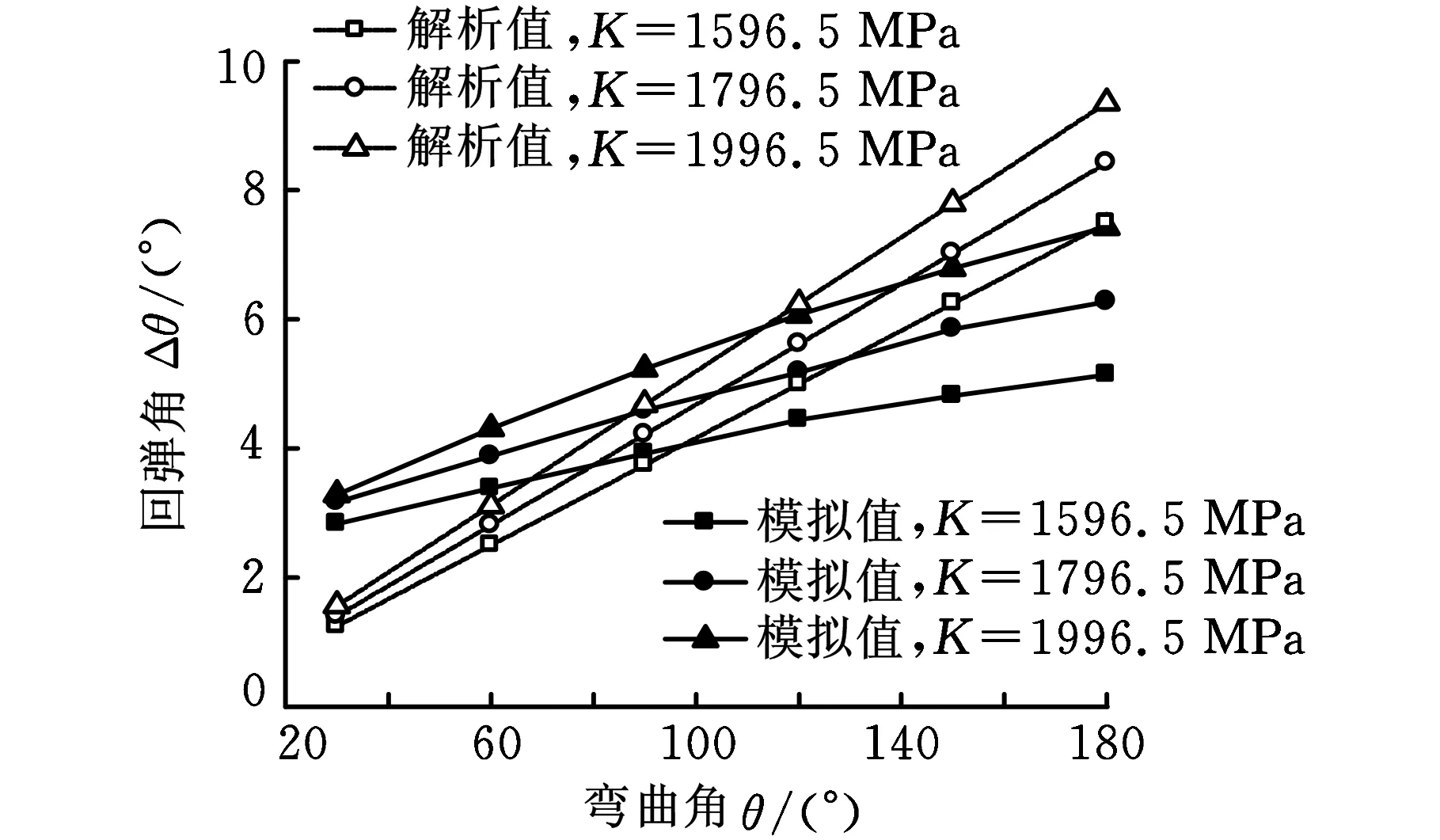
(a)强度系数K的影响

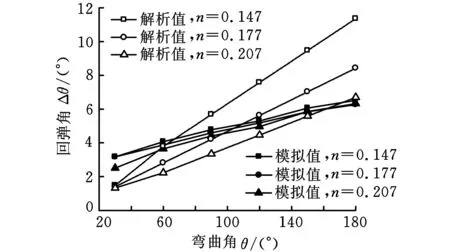
(b)硬化指数n的影响

(c)弹性模量E的影响图7　材料参数对回弹角的影响

2.3理论计算、有限元模拟和试验结果对比

根据文献[18]中的试验条件，应用本文所建立的理论解析模型和有限元模型分别对文献[18]中规格为φ14 mm×1.35 mm(管径×壁厚)的TA18钛合金管材数控弯曲回弹过程进行理论计算和数值模拟，并与试验结果进行对比。其中，文献[18]中的试验条件为：弯曲角θ分别为30°、60°、90°，弯曲半径R=35 mm，弯曲角速度ω=0.1 rad/s，侧推速度vp=3.5 mm/s，模具配置为弯曲模、夹紧模、助推块和芯棒。芯棒与管内壁采用20#航空润滑油进行润滑，其他管材与模具接触面不进行润滑。

图8所示为理论计算、有限元模拟结果与文献[18]所得的试验结果对比图。由图可知，采用本文建立的有限元模型，模拟计算得到的回弹角与试验值比较吻合，回弹角的平均相对误差在10%以内，说明本文所建立的有限模型是可信的。理论计算值和试验值对比误差较大，说明理论计算公式还有待根据大量试验加以修正，这主要是因为，在进行理论计算时采用了大量的假设，且没有考虑管材数控弯曲成形过程中管模实际接触条件及其他工艺参数的影响，使得误差较大，但理论解析模型仍然能够反映回弹角的变化趋势。因此，理论解析模型对深刻理解回弹潜在的物理变形机理具有一定的指导作用。

图8　理论计算、有限元模拟结果与文献[18]试验结果对比

3　结论

(1)基于21-6-9高强不锈钢管材弯曲时外侧壁材料受到弯曲切线方向的单向拉伸变形的假设，推导了最终弯曲半径和回弹角度的近似计算公式。

(2)管材弯曲卸载后的最终弯曲半径随着弯曲半径的增大而增大，随着强度系数的增大或弹性模量、硬化指数的减小而增大，并且与弯曲角度无关。

(3)管材弯曲的回弹角随弯曲角度的增大而呈线性增大，随相对弯曲半径、强度系数的增大或弹性模量、硬化指数的减小而增大。

(4)对比分析了理论解析，有限元模拟和试验结果，发现有限元模拟结果与试验结果吻合较好，能够较精确地预测回弹；理论解析与试验结果对比误差较大，但能够反映回弹角的变化趋势。

[1]Yang He, Li Heng, Zhang Zhiyong, et al. Advances and Trends on Tube Bending Forming Technologies[J]. Chinese Journal of Aeronautics, 2012, 25(1):1-12.

[2]Yang He, Zhan Mei, Liu Yuli, et al. Some Advanced Plastic Processing Technologies and Their Numerical Simulation[J]. Journal of Materials Processing Technology, 2004, 151(1/3):63-69.

[3]Hashmi M S J. Aspects of Tube and Pipe Manufacturing Processes: Meter to Nanometer Diameter[J]. Journal of Materials Processing Technology, 2006, 179(1/3):5-10.

[4]Levent S, Mehment A G, Deniz B, et al. Investigation and Prediction of Springback in Rotary-draw Tube Bending Process Using Finite Element Method[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2012, 226(12):2967-2981.

[5]Al-Qureshi H A, Russo A. Spring-back and Residual Stressesin Bending of Thin-walled Aluminum Tubes[J]. Materials and Design, 2002, 23(2):217-222.

[6]E Daxin, He Huahui, Liu Xiaoyi, et al. Spring-back Deformation in Tube Bending[J]. International Journal of Minerals, Metallurgy and Materials, 2009, 16(2):177-183.

[7]贾美慧，唐承统. 不锈钢管材弯曲成形回弹预测模型研究[J]. 北京理工大学学报，2012,32(9)：910-914.

Jia Meihui, Tang Chengtong. Springback Prediction Model on Tube Bending Formation of Stainless Steel[J]. Transactions of Beijing Institute of Technology, 2012,32(9):910-914.

[8]吴文云. AZ31和AM30镁合金管材弯曲成形及变形机理研究[D]. 上海：上海交通大学，2010.[9]Wu Wenyun, Zhang Ping, Zeng Xiaoqin, et al. Bendability of the Wrought Magnesium Alloy AM30 Tubes Using a Rotary Draw Bender[J]. Materials Science and Engineering A, 2008, 486(1/2):596-601.[10]Gu Ruijie, Yang He, Zhan Mei, et al. Research on the Springback of Thin-walled Tube NC Bending Based on the Numerical Simulation of the Whole Process[J]. Computational Materials Science, 2008, 42(4):537-549.

[11]Gu Ruijie, Yang He, Zhan Mei, et al. Springback of Thin-walled Tube NC Precision Bending and Its Numerical Simulation[J]. Transactions of Nonferrous Metals Society of China, 2006, 16(2): s631- 638.

[12]Jeong H S, Ha M Y, Cho J R. Theoretical and FE Analysis for Inconel 625 Fine Tube Bending to Predict Springback[J]. International Journal of Precision Engineering and Manufacturing, 2012,13(12):2143-2148.

[13]Zhan Mei, Zhai Huadong, Yang He. Springback Mechanism and Compensation of Cryogenic Ti Alloy Tube After Numerically Controlled Bending[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(2):s287-293.

[14]Li Heng, Yang He, Song Feifei, et al. Springback Characterization and Behaviors of High-strength Ti-3Al-2.5V Tube in Cold Rotary Draw Bending[J]. Journal of Materials Processing Technology, 2012, 212(9):1973-1987.

[15]Li Heng, Yang He, Tian Yuli, et al. Geometry-dependent Springback Behaviors of Thin-walled Tube Upon Cold Bending[J]. Science China Technology Sciences, 2012, 55(12):3469-3482.

[16]刘树勋，刘宪民，刘蕤，等. 0Cr21Ni6Mn9N奥氏体不锈钢的应变强化行为[J].钢铁研究学报，2005,17(4):40-44.

Liu Shuxun, Liu Xianmin, Liu Rui, et al. Work-hardening Behavior of 0Cr21Ni6Mn9N Austenitic Stainless Steel[J]. Journal of Iron and Steel Research, 2005,17(4):40-44.

[17] Jiang Zhiqiang, Yang He, Zhan Mei, et al. Coupling Effects of Material Properties and the Bending Angle on the Springback Angle of a Titanium Alloy Tube during Numerically Controlled Bending[J]. Materials and Design, 2010, 31(4):2001-2010.

[18]岳永保.钛合金管数控弯曲成形过程数值模拟及实验研究[D].西安：西北工业大学，2009.

(编辑郭伟)

Theoretical Calculation and FE Analysis of Springback for 21-6-9 High Strength Stainless Steel Tube during NC Bending

Fang Jun1,2Lu Shiqiang2Wang Kelu2Xu Xiaomei2Xu Jianmei2Yao Zhengjun1

1.Nanjing University of Aeronautics and Astronautics,Nanjing,211106 2.Nanchang Hangkong University,Nanchang,330063

In order to study the effects of geometric parameters and material parameters on springback of bent tube, the formulas of the final bending radius and springback angle were derived using the elastic plastic theory, then combined with theoretical and FE analysis, the effects of geometric parameters and material parameters on springback law of 21-6-9 high strength stainless steel tube during NC bending were analyzed, then the theoretical analysis, FE simulation and experimental results were compared. The results show that the final bending radius increases with the increase of bending radius, strength coefficient, or the decrease of elastic modulus and hardening exponent, and it is independent of bending angle. The springback angle increases with the increase of bending angle, relative bending radius, strength coefficient or the decrease of elastic modulus, hardening exponent. The simulation results and experimental ones agree with each other well, which can predict springback more accurately. Comparing theoretical analysis with experimental results, the error is bigger, but it can reflect the change trend of springback angle.

21-6-9 high strength stainless steel tube; NC bending; springback; theoretical analysis;FE analysis

2013-11-06

国家自然科学基金资助项目(51164030)

TG386DOI：10.3969/j.issn.1004-132X.2015.03.016

方军，男，1984年生。南京航空航天大学材料科学与技术学院及南昌航空大学航空制造工程学院博士研究生。研究方向为先进塑性成形技术及计算机仿真。鲁世强(通信作者)，男，1962年生。南昌航空大学材料科学与工程学院教授、博士研究生导师。王克鲁，男，1968年生。南昌航空大学材料科学与工程学院教授、博士研究生导师。许小妹，女，1989年生。南昌航空大学材料科学与工程学院硕士研究生。徐建美，女，1988年生。南昌航空大学材料科学与工程学院硕士研究生。姚正军，男，1968年生。南京航空航天大学材料科学与技术学院教授、博士研究生导师。