蛇形机器人的研究与发展综述

苏　中　张双彪　李兴城

1.北京信息科技大学，北京，100101　　2.北京理工大学，北京，100081

蛇形机器人的研究与发展综述

苏中1,2张双彪2李兴城2

1.北京信息科技大学，北京，1001012.北京理工大学，北京，100081

对国内外蛇形机器人进行了研究和分析，将其分为形态研究、运动学和动力学模型、步态控制及稳定性等研究内容，从二维运动和三维运动角度，对研究内容进行了综述、分析和总结。结合蛇形机器人的结构和运动步态特点，对国内外研制的蛇形机器人进行了分类，最后对蛇形机器人的研究发展进行了展望。

运动步态；运动学；动力学；控制方法；稳定性

0　引言

随着科技的不断发展，蛇形机器人作为新型可移动的柔性机器人，以其具有多步态运动能力，且能够适应复杂多变的环境的特点，成为机器人领域的一个研究热点。特别地，蛇形机器人的易于伪装、隐蔽性高、结构紧密和高集成化等特点，使其能够满足侦察、巡逻等军事需求，并且可通过空中投放到敌方阵地，利用自身携带的图像采集设备，完成侦察任务。未来的蛇形机器人还可装备一定的弹药，完成攻击或自爆等任务。

除军事应用外，蛇形机器人还具有较广的民用前景，如地震和火灾现场搜救、井下毒体检测、管道检测、核电站辐射检查、桥墩侵蚀检查等，在人员不便进入或难于进入的高危险领域，均可利用低成本的蛇形机器人代替操作人员，妥善地完成指派任务。结合这些优点和用途，近年来对于蛇形机器人的研究，得到国内外学者的广泛关注。

本文首先介绍生物蛇的基本步态，然后有针对性地研究了国内外蛇形机器人的研究成果，从形态研究、运动学模型和动力学模型、步态控制及稳定性分析等方面对理论研究进行综述，对已研制的蛇形机器人进行分类，并且对其研究现状和问题点进行分析，最后对蛇形机器人研究进行总结和展望。

1　生物蛇的运动形式

对于生物蛇的研究，最早起源于1946年，Gray[1]通过研究自然界的生物蛇，将其基本运动步态分为蜿蜒运动、直线运动、鼓风琴运动和侧移运动。蜿蜒运动(serpentine movement)是以侧向波传播为特征的运动步态，随着侧向波的传递，身体向前移动，此种步态被认为是生物蛇一种具有高效率的运动步态，适合地形平坦的环境。直线运动(rectilinear movement)是生物蛇通过肋骨、肌肉的交替运动，使身体向前爬行，此种方式与毛虫所采用爬行相似，其运动效率很低，常与其他步态联合使用，适用于狭窄区域。鼓风琴运动(concertina movement)，表面看来与蜿蜒运动相似，但其通过自身向前牵引，使身体向前爬行，通常生物蛇在树上爬行时采用此种步态。侧移运动(sidewinding movement)具有螺线形特征，可使身体横向或斜向运动，最典型的是生活在沙漠中响尾蛇的运动步态(也称作螺旋步态[2])，此步态使生物蛇具有更强的适应性。此外，生物蛇在沿树、杆等物体向上攀爬时采用的步态，也具有螺旋线特征，它是依靠螺旋内测与物体之间的摩擦力稳定身体，利用类似于弹簧伸缩功能，促进自身向上(前)运动。

2　蛇形机器人的理论研究状况

基于Gray对生物蛇运动步态产生机理的研究，在20世纪70年代，东京工业大学率先开始研究仿生蛇的运动步态，从此开启了智能机器人领域的又一扇大门——蛇形机器人。随后美国、挪威、中国等多个国家的研究者们纷纷加入到蛇形机器人的科研行列，逐渐开展由浅入深的研究。

蛇形机器人的理论研究是工程实验研究之基础，综合国内外对于蛇形机器人的研究成果，主要包括形态研究、运动学和动力学模型、步态控制及稳定性分析三大块内容。

2.1形态研究

经历了自然法则优胜劣汰的选择，生物蛇所具有的运动步态是无足脊椎动物行走步态的典范。国内外学者通常将拟定的形态曲线作为理想的运动曲线，控制蛇形机器人的运动曲线向理想形态曲线逼近，逼近的形态曲线越流畅自然，越贴近实际，仿生爬行效率越高。在研究蛇形机器人运动步态时，采用不同的形态曲线具有不尽相同的爬行效果。为建立合理的运动形态，国内外展开了研究，并取得了一些成果。

蜿蜒运动是目前国内外研究最多的一种二维步态，所具有的侧向波传递过程，与正弦曲线变化相似，相位和波动幅值随着时间发生变换。Clothoid曲线是通过对两个具有半周期的Cornu螺旋线联合而成的，可作为蜿蜒运动逼近，但两个螺旋线在连接点处并不连续，存在奇异点问题[3]。Hirose[3]通过对生物蛇运动的实验和观察，提出了用于逼近蜿蜒运动的Serpenoid曲线，并与正弦曲线和Clothoid曲线进行实验对比及分析，结果显示Serpenoid曲线具有较好的模拟效果。Ma[4]提出了Serpentine曲线，从运动效率角度证明了该曲线比Serpenoid曲线具有更好的模拟效果。

当生物蛇沿杆向上攀爬或侧移运动时，运动形态体现为三维螺旋曲线，为准确描述该曲线， Yamada等[5]采用Frenet-Serret方程，建立运动外形的三维曲线模型，Burdick等[6]通过分析侧移运动过程，将蛇体结构分为地面接触部分和拱形部分，采用分段形式建立三维运动曲线，孙洪等[7]针对无轮结构的蛇形机器人，建立了基于螺旋角的等距螺旋曲线，以上方法均具有较好的逼近效果。

2.2运动学模型和动力学模型

运动学模型和动力学模型是蛇形机器人的控制基础。基于前人对生物蛇形态曲线的初步探索，为深入研究蛇形机器人步态，运动学模型和动力学模型成为该领域的研究重点。根据蛇形机器人的运动步态特点，可以将运动学模型和动力学模型分为二维步态和三维步态两种。

2.2.1二维步态

蛇形机器人的二维步态主要指的是蜿蜒、内攀爬和蠕动(也称行波步态)。蜿蜒步态与生物蛇的蜿蜒运动相同，蠕动步态犹如尺蠖蠕动，但其效率很低，内攀爬步态类似于鼓风琴运动，但是利用机器人两个外侧表面与外界的接触摩擦力，及自身部分向前运动。

蜿蜒运动作为具有高效率的运动步态，成为学者们对二维步态的主要研究对象。Hirose[3]对生物蛇运动过程进行了观察和骨骼解剖分析，建立了连杆机构作为蜿蜒步态的运动学模型，以及平面和坡面地形条件下动力学模型，从数学角度得出蜿蜒运动的产生条件为摩擦力存在各向异性，并且发现生物蛇在爬行时，位于蜿蜒曲线两侧波峰处的腹部会向上抬起，将此运动称作Sinus-lifting。随着对Sinus-lifting运动研究的不断深入，Yamada等[8]提出了弧形结构的蛇形关节，通过仿真和实验进行初步验证。Hu等[9]建立了切向和法向的摩擦力模型，并在不同角度的坡度下，对生物蛇进行了爬行实验，进一步证明了蜿蜒运动的产生条件。Kelly等[10]、Ostrowski等[11]针对装有三个从动轮的连杆型蛇形机器人，利用拉格朗日法建立了蜿蜒动力学模型，并进行了可控制性分析。Nilsson[12]通过对动力学模型的理论推导，得出即使在各向同性的摩擦力作用下，仍存在效率低的蜿蜒运动的结论。Shapiro等[13]在Walton的摩擦力模型基础上，建立了蛇形机器人内攀爬方式的摩擦力表达式，在常规、线性和非线性三种摩擦力情况下，研究法向摩擦力和切向摩擦力的特性。为提高蛇形机器人对外界复杂环境的适应性，Liljeback等[14]分析了机器人自身与障碍物之间的位置关系，提出了平面运动的障碍辅助运动步态，建立了蛇形机器人的动力学模型。Rincon等[15]通过对四连杆蛇形机器人的蠕动步态分析，建立了运动学模型和动力学模型。

国内对蛇形机器人二维步态的研究也取得了一些成果。Ma等[16]建立坡面地形条件下的运动学模型、动力学模型，研究了坡面角度与摩擦力之间的关系，通过对无侧滑条件下的运动步态进行仿真，确定了步态实现的优化参数。李斌等[17]提出了基于乐理的步态控制方法，通过定义乐理符号、规则等，实现了蛇形机器人蜿蜒运动控制。张佳帆等[18]通过对生物蛇蠕动步态分析，建立了蠕动步态的运动学模型。孙洪等[19]受蜿蜒运动的启发，在分析了蠕动步态的波形传播机理基础上，将Serpenoid曲线作为蠕动的驱动函数，并通过实验验证了可行性。

2.2.2三维步态

蛇形机器人的三维步态包括侧移步态和攀爬步态，两种步态与生物蛇的运动相同，并且均具有螺旋曲线的特点。

Chirikjian[20]从几何角度定义了两个螺旋线方向角，通过建立单位弧长的表达式，进而建立了全长度的螺旋侧移运动的运动学模型，并通过计算机对侧移和转弯进行定性仿真。

Hatton等[21]分析了螺旋侧移运动的特点，认为在坡面地形条件下，生物蛇的侧移运动曲线为椭圆螺旋曲线，建立了身体和地面接触点与椭圆之间的几何关系式。Gong等[22]基于前人的研究基础，提出了利用侧移运动的锥形螺旋曲线，实现蛇形机器人绕固定点侧移转弯的方法。

为了让蛇形机器人运动曲线平滑，Yamada等[5,8]提出了弧形连杆结构，基于Frenet-Serret方程，建立了弧形结构的三维模型，针对Sinus lifting运动进行仿真和实验验证，结果表明运动曲线平滑。

国内对三维步态的动力学模型研究很少，孙洪[23]在研究攀爬型蛇形机器人时，提出三连杆蠕动方式，在理想情况下，建立了攀爬的数学模型。

二维运动学和动力学模型的研究成果很多，为三维步态的研究铺垫了理论基础。根据蛇形机器人的实际工作环境的复杂性，三维步态的运动学模型和动力学模型需要进一步研究。

2.3蛇形机器人的步态控制及稳定性分析

对蛇形机器人的步态控制分为二维步态控制和三维步态控制。目前的研究成果主要着重于二维步态控制，通常情况下，采用开环控制即可实现蛇形机器人的步态运动，而为控制蛇形机器人运动智能地、高效率地运动，需要研究闭环的控制系统实现步态控制。

目前，关于蛇形机器人控制方法的研究很多，都是基于动力学模型，建立每个关节角数学关系式，从而设计步态控制器。Date等[24]在侧滑约束力的条件下，根据蛇形机器人头部速度，设计头部跟踪已规划路径的跟踪率，实现了对机器人的路径控制。Prautsch等[25]提出蜿蜒运动的速度控制方法，通过李亚普诺夫方程得到控制方程，以控制输入量的大小衡量系统能量消耗水平，得出了约束为功耗最小时，蜿蜒运动的速度控制参数。为避免蛇形机器人的直线状态的奇异情况，Matsuno等[26]分别设计了动态操纵性和约束力的价值函数，通过控制身体形状来满足价值函数。Li等[27]建立了蛇形机器人的动力学模型，采用被动控制方法设计了控制器，并用李亚普诺夫理论验证了系统的稳定性。为解决关节受外界环境阻碍，而导致蛇形机器人无法运动的问题，Liljeback等[14]建立接触力和相对角的关系，设计了关节相对角的比例-微分控制器，该控制器通过对机器人的接触力的测量，调整关节相对角，实现障碍辅助自适应的前进步态，同时利用非线性理论分析了二维步态控制系统，得出蛇形机器人渐进稳定到平衡点的控制率是时变的，并且当与地面的摩擦力为各向同性时，系统不可控，当为各项异性时，系统为强可达到的结论。他们还建立了路径跟踪控制器，利用庞加莱映射分析了该控制器的稳定性[28]。

国内从事蛇形机器人的科研单位在控制方法上也取得了一些成果。为实现轮式蛇形机器人的蜿蜒运动，Ma等[29]以轮高、头部的方向角和头部的高度作为状态变量，将各关节的相对转角作为控制量，设计闭环控制回路，仿真结果显示，在蜿蜒曲线控制的同时，头部位置和方向均得到较好的控制效果。陈丽等[30]针对三维侧向运动看作水平方向和垂直方向蜿蜒运动的复合，建立了空间运动方程。为研究蛇形机器人缆索攀爬步态，魏武等[31]采用迭代链拟合方法和关键帧提取的联合方法，对蛇体曲线进行拟合并生成运动步态。卢振利等[32-34]通过分析神经元模型的特性，提出采用循环抑制的中枢模式发生器(CPG)，控制蛇形机器人的二维和三维步态，以及实现步态转换，又提出层次化联结CPG模型，控制机器人的三维步态，该方法不完全依赖动力学模型，可根据控制器的输出规律，实现对机器人关节的转角控制，从而实现蜿蜒运动。王智锋等[35]从能量传递的角度，提出了被动蜿蜒控制方法，该方法能够让蛇形机器人不主动测量环境信息，依靠自身能量状态被动地适应环境。Wu等[36]通过分析单向连接的CPG模型，提出了反馈式CPG模型，初步分析了CPG参数对蜿蜒运动的影响，从仿真和实验两方面验证了步态控制的反馈式CPG模型。

3　蛇形机器人的本体研究状况

几十年来，经过国内外学者们的不懈努力，对蛇形机器人的研究成果不但体现在理论上，而且本体样机的研制上，也结出了可喜硕果，国内外涌现出不同种类、不同功能的蛇形机器人。

3.1国外蛇形机器人

图1　ACM-R5

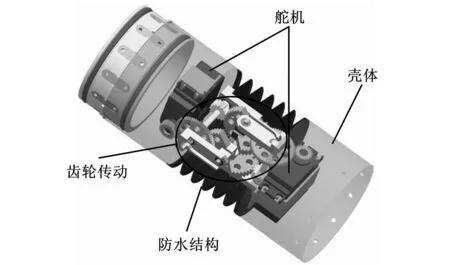
图2　ACM-R5的关节内部结构

Hirose[3]提出了Active Cord Mechanism蛇形机器人，其率领的科研团队于1972年研制出世界上第一架命名为ACM 的蛇形机器人，随着研究的深入，先后研制出具有代表性的ACM-Ⅲ、ACM-R2、ACM-R3和ACM-R4等陆地蛇形机器人，这些机器人已经从简单的二维运动，发展到了适应凹凸不平的崎岖地面。为满足水下探测需要，该团队又研发了名为ACM-R5的水陆两栖蛇形机器人，如图1所示。该机器人的关节设计了一对驱动伺服电机，通过齿轮系传动，可实现俯仰和偏航运动，如图2所示。在每个节躯干单元的外侧，每隔60°安装一个带有小从动轮的叶片，这样，在关节进行防水处理后，ACM-R5既可实现陆上的蜿蜒、翻滚和侧向运动，又可实现水下的自由游动，并且其游动速度不少于0.9 m/min。在机器人的头部装有一部摄像头，凭借自身的无限传输功能，可以将摄像头采集到的数据传输给上位机，以便进行数据处理[3,37-39]。该蛇形机器人可通过尾部的电源接口实现有线供电，当进行水下作业时，也可通过自身携带的聚合物锂电池进行自主供电。

德国国家信息技术研究中心于20世纪末，先后研制出GMD-Snake和GMD-Snake2，如图3和图4所示。GMD-Snake头部带有用于探测障碍物的压力传感器和照明用的LED灯，各个关节装有检测角度的弹簧触点装置，以及用于控制水平和垂直方向的驱动电机，该机器人能够完成平地爬行和越障爬行[40]。

图3　GMD-Snake

图4　GMD-Snake2

基于GMD-Snake功能和结构的研究，GMD-Snake2的头部装有一个用于图像识别的摄像头，每节躯干单元的壳体都由圆柱形铝材构成，其关节与GMD-Snake相同，通过两个电机连接而成的万向节实现，如图5所示。在壳体外侧每隔60°安装一对小从动轮，壳体内部装有感知运动状态的加速度传感器，以及用于测量距离的机械-光学传感器。与GMD-Snake相同，需要外部提供24V电源[41]。

图5　GMD-Snake关节

图6　OmniTread 蛇形机器人结构

美国密歇根大学研制的OmniTread OT-4和OmniTread OT-8蛇形机器人具有独特的结构，如图6所示，该系列机器人由7节躯干单元组成，每个单元具有各自的作用。单元1为有效载荷单元，单元2和单元6为空气压缩器，单元3和单元5为能源单元，单元4为驱动单元。在每个躯干单元外与地面接触的平面上分别装有一对履带，以保证机器人发生机体翻时仍具有足够的爬行能力。躯干单元之间设计了气动二自由度的关节，利用气动驱动关节可实现OmniTread机器人的俯仰和偏航运动。

OmniTread蛇形机器人利用两块并联的7.4 V、730 mA·h的聚合物锂电池作为驱动电源，安装在驱动电机两侧。OmniTread OT-8与OmniTread OT-4不同之处在于可实现无线操控，可通过直径为23.32 cm(8 inch)的管道，而OmniTread OT-4需要有线操控，仅能通过直径为11.16 cm(4 inch)通道。在脊柱结构内OmniTread机器人具有很强的翻越能力，能够适应丛林、戈壁、管道等崎岖环境，爬行速度可达到0.9 m/min[42]。

美国Gavin Miller带领团队研制了S系列的蛇形机器人，其中，S5蛇形机器人具有极高的仿生效果，如图7所示。该机器人由64个伺服电机和8个伺服控制躯干单元组成，每个单元的内部结构如图8所示，可见该结构仅能进行偏航运动。此外，S5自身携带的42块聚合物锂电池完成供电。由于S5的躯干关节数量大、长径比小，所以平面蜿蜒运动具有极高的仿生效果。

图7　蛇形机器人S5

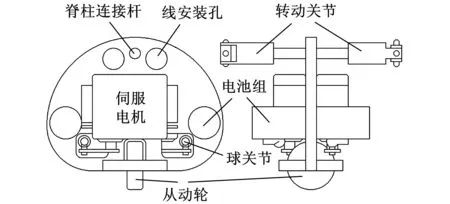
图8　S5蛇形机器人的躯干单元结构简图

为实现距离检测、运动测量、图像采集、转动等功能，Gavin Miller对最新款的S7蛇形机器人集成了多种传感器，如图9所示[43]。

图9　蛇形机器人S7

美国卡耐基梅隆大学主要研究用于攀爬的模块化蛇形机器人，具有代表性的蛇形机器人为Uncle Sam，如图10所示。该机器人研制考虑了尺寸、功耗和速度等因素对步态控制的影响，机身全长为94 cm，直径为5.1 cm。图11为模块的示意图。每个模块装有一个伺服电机，通过减速结构实现驱动杆的动力输出，并且驱动杆与连接杆正交设计，将两个模块进行连接后，水平方向的驱动杆可实现偏航运动，铅垂方向的驱动杆可实现偏航运动。

图10　蛇形机器人Uncle Sam

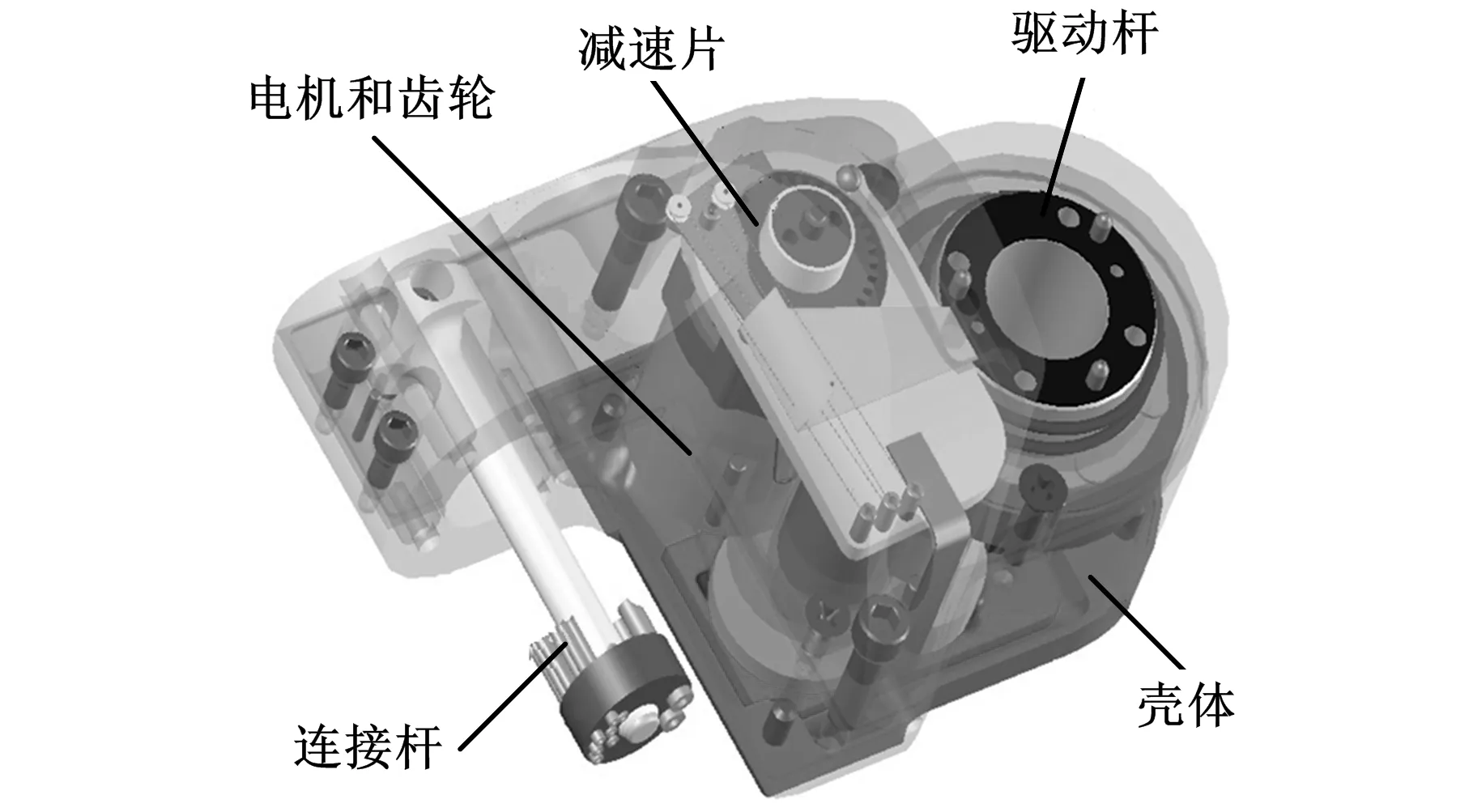
图11　单模块的结构示意图

卡耐基梅隆大学模块化蛇形机器人采用螺旋步态实现向前爬行，具有很强的翻越能力，根据攀爬方式不同，分为内攀爬式和外攀爬式两种，二者均以自身和外部环境的摩擦作为力学约束条件，通过身体的运动，实现沿壁或杆(柱)体爬行，适用于空间狭窄的管道、墙壁狭缝、杆(柱)体等环境爬行。该机器人结构节凑运动灵活的特点，需要有线控制和外接电源[44-45]。

卡内基梅隆大学协助研发了一种铂硅复合的皮肤，既能保护机器人机构，还能适应湿地、沙地、灌木丛等环境，进而研制了一种具有皮肤驱动能力的蛇形机器人(TSDS)，通过控制皮肤向后运动，实现身体向前运动，如图12所示[46]。

图12　皮肤驱动的蛇形机器人TSDS

挪威科技大学研发了用于火灾扑救的蛇形机器人Anna Konda，其体型较大，躯干采用金属材料加工，具有20个液压马达，身长为3 m，总质量为75 kg。该机器人头部带有两个灭火剂喷嘴，当火灾发生时，可对准火源进行扑救，如图13所示[47-48]。

图13　蛇形机器人Anna Konda

为深入研究障碍辅助运动步态，挪威科技大学又研制了名为Aiko和Kullo的蛇形机器人，如图14、图15所示，尽管二者为无轮式的蛇形机器人，但均可实现多步态运动[49-50]。Aiko身长1.5 m，总质量7 kg，采用直流电机驱动，需外接电源供电，未携带任何传感器。

图14　蛇形机器人Aiko

图15　蛇形机器人Kullo

而对于由10节躯干单元组成的Kullo，每个的单元均装有压力传感器，可感知机器人自身与外界的作用力。Kullo的躯干单元具有光滑的球型外壳，包裹着一个环形和两个半环形的金属框架，通过两个输出轴为正交安装的伺服电机，以及齿轮系的传动装置，可实现水平方向的框架发生俯仰，铅垂方向的框架发生偏航运动，躯干单元的示意图如图16所示。

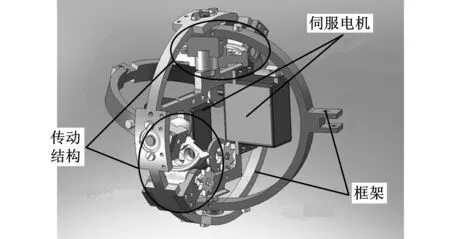
图16　Kullo躯干单元的结构示意图

3.2国内蛇形机器人

我国对蛇形机器人本体的研制稍晚于国外，但研发脚步逐渐赶上国外发展水平，近年来也取得了可喜成果。

中国科学院沈阳自动化研究所以马书根为核心的机器人研发团队，通过与日本合作，共同研制出具有代表性的蛇形机器人巡视者Ⅱ和探查者Ⅲ，如图17和图18所示。

图17　巡视者Ⅱ

图18　探查者Ⅲ

巡视者Ⅱ由金属材质的躯干单元组成，全长约1.2 m，总质量8 kg，单元间通过特有的万向节链接，能够实现俯仰、偏航和滚转三轴转动，每节躯干单元周围装有“体轮”，可减小运动阻力，提高运动效率，其头部装有视觉传感器和GPS系统，用来辅助运动控制。此外，该机器人可自身携带电源，以及实现无线操控[51]。

基于对巡视者Ⅱ的研究，探查者Ⅲ可实现水陆两栖复杂环境的运动，共由9节躯干单元组成，总长1.17 m，总质量6.75 kg。为适应水下环境，在躯干单元的径向，每间隔45°安装一个带有从动轮的浆，而取代了“体轮”，并且在单元之间增加了防水密封装置。单元内采用两个伺服电机驱动，通过齿轮系传动实现俯仰和偏航运动，单元结构如图19所示，当左右齿轮同向运动时，发生俯仰运动，当左右齿轮发生相反方向运动时，发生偏航运动[52]。

图19　探查者Ⅲ的单元结构

上海交通大学研制的适合于攀爬的CSR机器人，全长约1.5 m，总质量约2.7 kg，由15个具有俯仰和滚转功能的躯干单元组成，外面包裹一层增大接触力的胶带，如图20所示[53]。

图20　蛇形机器人CRS

与其他类型机器人不同，该机器人的躯干单元两端可实现绕径向转动，中间可绕轴向转动，改变径向转动的角度，从而实现机器人能绕柱体攀爬，如图21所示。

图21　蛇形机器人CRS的躯干单元

国防科技大学研制的蛇形机器人(简称NUDT SR)，总长1.2 m，总质量1.8 kg，可实现蜿蜒运动，最大前进速度可达20 m/min，其头部带有视频采集装置，如图22所示[54]，然而目前关于该机器人的资料很少。

图22　国防科技大学的蛇形机器人

北京信息科技大学正在研制一种新型的蛇形机器人“中国龙”(图23)，全长约1.2 m，总质量约2.6 kg。该机器人9个躯干单元构成，以及头、尾关节，其中一节为分体单元。躯干单元内部装控制系统和聚合物锂电池组，而分体单元内部装有一个伺服电机。单元之间通过伺服电机连接，水平安装的电机实现俯仰运动，铅垂方向的电机实现偏航转动。躯干单元间隔装有一对从动轮，从动轮与单元之间通过伺服电机连接，实现自身变形，结构简图如图24所示。

图23　蛇形机器人“中国龙”

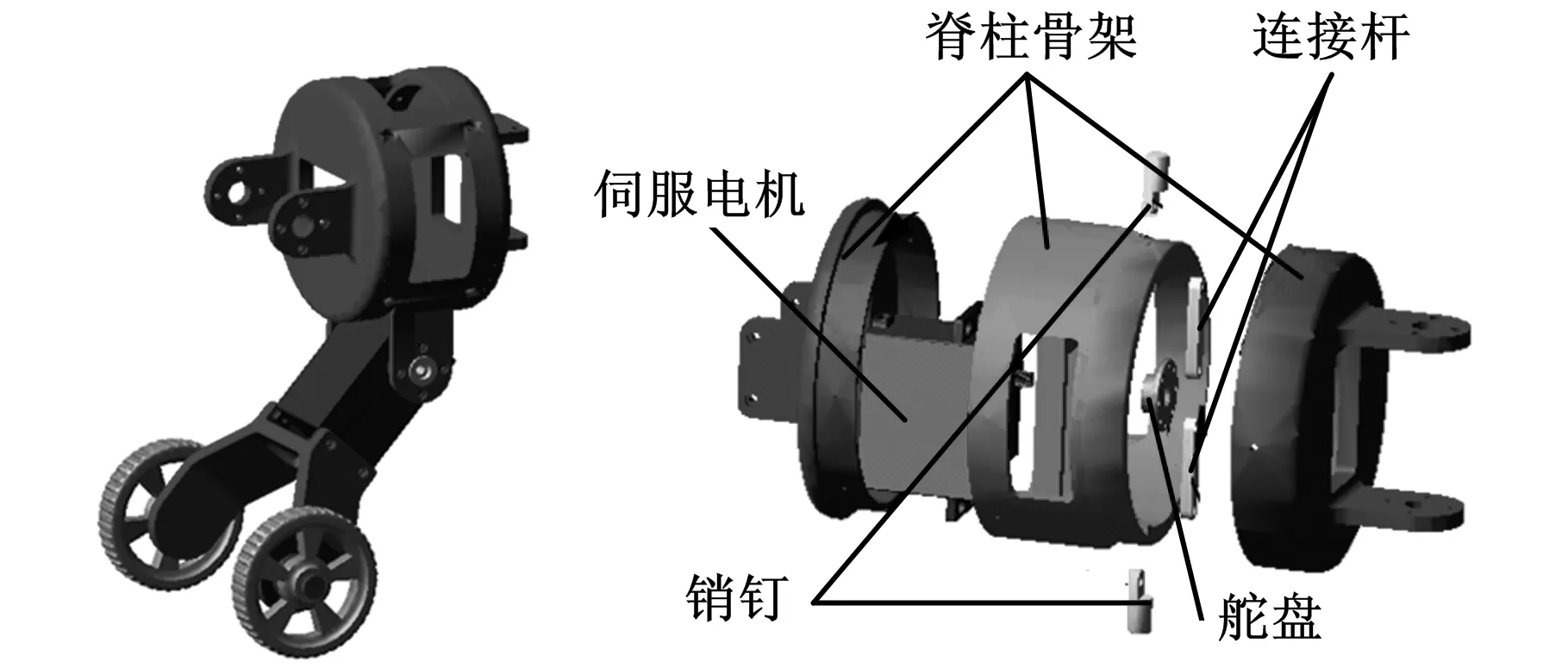
图24　“中国龙”的躯干单元和分体单元

“中国龙”机器人不但具有多种运动步态，而且能够利用自身穿戴带有温湿度、气体、压力等传感器的全织物皮肤，感知外界环境变化，并能采用分体、变形方式调整自身参数，以适应复杂恶劣的环境，如图25所示。

图25　具有感知功能的全织物皮肤

3.3蛇形机器人分类

国内外研制的蛇形机器人，在结构上主要有两大特点，一是连接机器人躯干单元的连接关节转动功能，二是机器人与外界接触的轮关节。

目前，蛇形机器人躯干单元均采用连杆式结构，躯干单元根据单轴转动、双轴转动和三轴转动的实现情况，可进行分类。将单轴转动的关节按照转动轴的平行安装，可称为单轴平行安装方式的单轴转动关节，可实现蛇形机器人的蜿蜒和蠕动。而将单轴转动的关节按照转动轴的非共面正交安装，可称为非共面单轴正交安装方式的双轴转动关节，不仅能够实现蜿蜒和鼓风琴运动，还能完成侧向运动和攀爬运动。还有一种将单轴转动的关节按照转动轴的共面正交安装，可称为共面轴正交安装方式的双轴转动关节，如CRS。还有一种双轴转动关节是通过齿轮系设计，实现俯仰和偏航，如ACM-R5和Kullo等。三轴转动关节不但可以实现俯仰和偏航运动，还能够绕躯干单元的轴线方向进行转动，如GMD-Snake2，尽管由此结构组成的蛇形机器人能实现三维运动，但对伺服电机的输出力矩要求很高，从而导致机器人的尺寸大，功耗大。

轮关节可分为主动轮和从动轮，主动轮能够提高爬行能，从动轮是为满足机器人在蜿蜒运动时摩擦力的各向异性条件而设计的。根据运动步态和功能的不同，蛇形机器人可以有从动轮结构和无从动轮结构。根据这两个特点，可以将前面所述蛇形机器人进行分类，如表1所示。

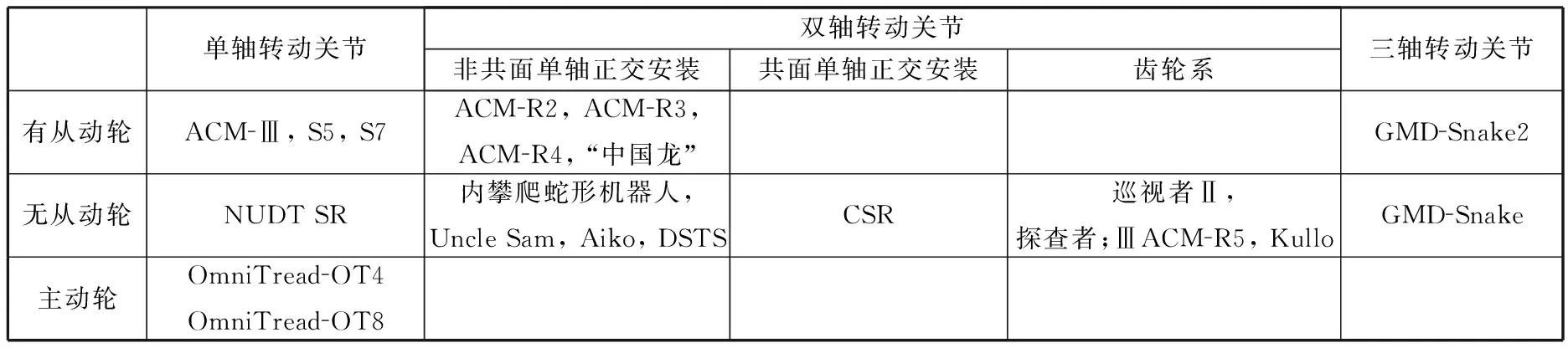
表1　按结构对蛇形机器人分类

从步态实现的角度，可以对表1所示的机器人进一步划分，具体内容如表2所示。

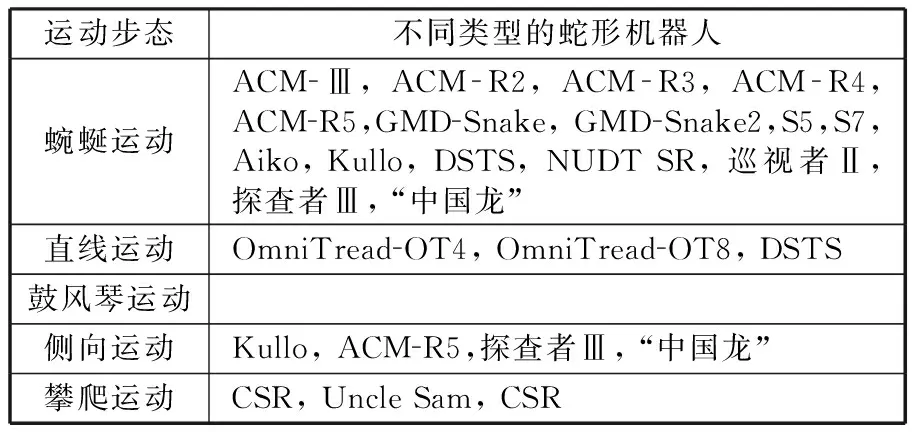
表2　按运动步态对蛇形机器人分类

4　蛇形机器人研究现状分析

综上对蛇形机器人理论和本体样机的研究，从如下4个方面对其进行分析。

4.1运动性能分析

蛇形机器人的运动步态研究得到一定程度的发展。蜿蜒运动是一种具有高效率的运动步态，成为步态研究重点，其他步态如蠕动、攀爬等也均得以实现，但这些步态与生物蛇相比，仿生效果尚存在一定差距。目前的蛇形机器人大多具有平面运动能力，但三维运动能力匮乏。究其原因，可以总结为如下三点：一是蛇形机器人躯干单元采用单轴转动关节。生物蛇在空间上可灵活转动，使自身展现出更好的柔性效果，而蛇形机器人必须采用具有双轴或三轴转动关节，才能达到模拟生物蛇运动的逼真效果。二是躯干单元尺寸大，输出效率低，导致运动效果不佳，所以需要实现伺服电机小型化。三是三维运动理论研究处于瓶颈，仍需要进一步完善。现有的成果正处于蛇形机器人理论研究的初步探索阶段，主要以适合平坦路面的二维运动为重点，对于运动产生机制、步态节奏控制方法等方面具有探索性的研究意义，而对于空间三维运动研究甚少，如当机器人遇到低矮障碍时，或外界干扰引起身形发生大幅度变化时，凭借现阶段的理论水平很难顺利完成翻越运动，或调节自身体形适应环境，并向前运动。可见，对于蛇形机器人运动理论研究尚不够，远不足以构建研发高仿真蛇形机器人的理论框架。

4.2功能特性分析

经过对蛇形机器人不断研发，其运动能力开始向实现复杂运动方向发展。双轴转动关节的研制提高了机器人的灵活性和集成度，为三维运动的高仿生运动提供了基础。尝试性地将适应领域从陆地向水陆两栖发展，使蛇形机器人不仅具有陆地爬行能力，还具有水中的游动能力。

最新研发的蛇形机器人具有了一定的环境感知能力，其集成的压力、视觉、距离、角度、速度等传感器，使机器人能掌握所处环境的相关信息，通过数据融合技术，可调节其适应环境的控制参数，满足该环境下的运动要求。除此之外，蛇形机器人在结构上开始向具有变形、分体等新功能发展，这样结合多传感器融合技术，使其时刻敏感外部环境，可进行分体协同运动，以及完成必要的变形运动。这些都为机器人的自主运动实现提供了基本条件。

然而，在实现这些功能过程中，仍然存在一些问题需要克服。水陆两栖机器人在水中需要不断运动，由于密封部位处于周期性交替拉伸和舒张过程，长时间工作引起密封部位出现疲劳开胶，导致内部漏水，控制系统无法正常工作，这便为机器蛇防水关节的密封性和续航时间提出了一定挑战。对于暴露在外界的关节，其容易受到外界猛烈的碰撞而破坏，所以需要选择合适的结构和高强度的材料作为加工的原材料，或者采用设计外加关节的保护套等措施来应对。对于某些工作环境，仅仅依靠躯干单元的伺服电机机动力实现运动，不能得到有效的、高效率的爬行结果，可以考虑通过对从动轮施加动力，成为驱动轮，增强运动能力。在集成电路的设计上，需要格外考虑系统在集成各种传感器后的可靠性问题，如散热等。为满足多功能、长续航的工作要求，蛇形机器人在保证低负载、便携带的条件下，需要装配体积的高容量电池。

4.3运动环境分析

蛇形机器人的运动环境开始从二维平面环境向三维复杂环境发展。纵观蛇形机器人的理论研究，均以结构环境为应用背景(即外界环境为已知的、有规则的)，主要以平面的二维运动为主，适合实验室研究，核电站等具有平坦路面的工作环境。对于丛林、草地、戈壁、震灾废墟等多障碍、甚凹凸、极崎岖等非结构环境的应用，蛇形机器人的应用便具有很大的局限性，需要深入研究三维运动。况且，对于运动控制的研究，一种是以动力学为基础的有模型控制，另一种是以神经生理学CPG为主的控制方法。基于动力学模型的控制方法，在结构环境下运动控制研究具有清楚、直观和便于理解的特点，但对于非结构环境下，基于该方法建立的模型则会及其复杂。而对于CPG控制方法，不依赖机器人精确的物理模型，便提供较可靠的控制信号，并且，此控制方法具有很好的稳定性，可结合自适应控制理论，提高蛇形机器人运动步态的仿生效果。

4.4项目资助分析

随着国内外对蛇形机器人的关注度不断提高，对该领域的研究在不同国家得到格外重视，均取得了高水平的科研资助。

日本对蛇形机器人的资助，主要包括教育部科学、体育、文化、财政资助科学研究先进机器人研发的创新工程项目，国际救援系统研究所和国立地球科学防灾研究所共同资助的社会防震减灾项目等。美国对蛇形机器人研究受到了国家科学基金、国防部高级研究计划局等的顶级资助，而且也得到了海军青年研究学者部门的资助。

在我国，蛇形机器人研发同样倍受重视，得到了国家、省地方的重点资助，其中包括国家自然科学基金、国家高技术研究发展计划(863计划)、中国科学院知识创新工程青年人才领域前沿项目、北京市科技计划项目、北京市教委创新能力提升计划项目、中央高校基本科研业务费专项资金项目、湖南省张花高速公路支持项目、交通运输部西部交通建设科技项目等资助。

5　结论与展望

针对现代战争信息化、民用领域的广泛需求，结合蛇形机器人易于伪装、隐蔽性高、结构紧密和高集成化等特点，本文对国内外近40年的仿生蛇的理论研究和本体研制状况进行了有针对性的研究。

根据生物蛇具有的蜿蜒运动、直线运动、鼓风琴运动和侧移运动等的基本步态，国内外提出了描述二维运动的Clothoid、Serpenoid和Serpentine曲线，建立了三维运动的螺旋曲线。为实现蛇形机器人的步态控制，从不同角度建立了的二维和三维的运动学模型和动力学模型，由此设计不同种类的步态控制器，并在稳定性分析方面做了一定的研究。纵观蛇形机器人本体研制状况，日本、美国、德国、挪威、中国等国家通过不懈努力研发，研究了具有不同功能的蛇形机器人，本文根据机器人结构和运动步态的特点，对蛇形机器人进行了分类。而且，这些研究得到了不同国家的关注，得到了重要项目的大力资助。

尽管目前对蛇形机器人的研究已取得了一定的研究成果，但为提高其适应能力，未来的工作需要从不同角度对蛇形机器人进行深入研究。

在运动能力方面，三维运动能力将全面提高蛇形机器人的运动能力，满足适合复杂的、非结构环境的需要，同时，将会加快并完善机器人由地面运动向水下运动的研究。结合生物蛇的其他运动能力，直立、攻击等运动的研究也会逐渐走进视线。

在结构方面，在研究小型化伺服电机的基础上，蛇形机器人的躯干单元将会得到进一步的改进，并能够提高机器人的柔性和灵活性。随着变形结构、分体结构应用，蛇形机器人对复杂、危险环境的适应能力和生存能力将会大幅度提高。

在感知功能方面，全织物皮肤的研制为感知能力的探索开起了先河，视觉识别、视觉测距、气体识别、辐射探测等功能均将得到重点研究，而且，根据不同传感器的应用特点，不同种类的感知皮肤会应运而生，具有感知能力的蛇形机器人将会在机器人领域如雨后春笋般地涌现在智能舞台上。

在工程实现方面，自给供电将便于蛇形机器人的运动，并有助于工作人员携带。这将会推进对于高性能小型化电池发展的研究步伐，有望解决小型机器人长航时的能源供给问题。随着蛇形机器人多功能高集成化发展，大数据无线传输技术将会促进控制系统软件、硬件向人机交互多智能系统发展，相信未来的蛇形机器人能够胜任复杂、恶劣、危险环境的工作要求。

[1]Gray J. The Mechanism of Locomotion in Snakes[J]. Journal of Experimental Biology,1946, 23(2): 101-124.

[2]郁树梅, 马书根, 李斌, 等. 蛇形机器人步态产生及步态分析[J]. 机器人, 2011, 33(3):371-378.

Yu Shumei, Ma Shugen, Li Bi, et al. Gait Generation and Analysis for Snake-like Robots[J]. Robot, 2011,33(3):371-378.

[3]Hirose S. Biologically Inspired Robots (Snake-like Locomotors and Manipulators)[M]. Oxford:Oxford University Press, 1993.

[4]Ma S. Analysis of Snake Movement Forms for Realization of Snake-like Robots[C]//Proceedings of the 1999 IEEE, International Conference on Robotics& Automation.Detroit, Michigan, 1999: 3007-3013.

[5]Yamada H, Hirose S. Study on the 3D Shape of Active Cord Mechanism[C]//Proceeding of the 2006 IEEE International Conference on Robotics and Automation.Orlando, Florida, 2006:2890-2895.

[6]Burdick J W, Radford J, Chirikjian G S. A Sidewinding Locomotion Gait for Hyper-Redundant Robots[C]//IEEE International Conference on Robotics and Automation.Atlanta, GA, 1993:3007-3013.

[7]孙洪, 刘立祥, 马培荪. 攀爬蛇形机器人爬树的静态机理研究[J]. 机器人, 2008, 30(2): 112-122.

Su Hong, Liu Lixiang, Ma Peisun. On the Tree-Climbing Static Mechanism of a Snake Robot Climbing Trees[J]. Robot, 2008, 30(2):112-122.

[8]Yamada H, Hirose S. Approximations to Continuous Curves of Active Cord Mechanism Made of Arc-shaped Joints or Double Joints[C]//2010 IEEE International Conference on Robotics and Automation.Anchorage, Alaska, 2010: 703-708.

[9]Hu D, Nirody J, Scott T, et al. The Mechanics of Slithering Locomotion[J]. PNAS, 2009, 106(25): 10081-10085.

[10]Kelly S, Murray R. Geometric Phases and Robotic Locomotion[J]. Journal of Robotic Systems, 1995, 12(6): 417-431.

[11]Ostrowski J, Burdick J. The Geometric Mechanics of Undulatory Robotic Locomotion[J].The International Journal of Robotics Research, 1998, 17(7): 683-701.

[12]Nilsson M. Serpentine Locomotion on Surfaces with Uniform Friction[C]//Proceedings of 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems.Sendal, Japan, 2004:1751-1755.

[13]Shapiro A, Greenfield A, Choset H. Frictional Compliance Model Development and Experiments for Snake Robot Climbing[C]//2007 IEEE International Conference on Robotics and Automation.Roma, Italy, 2007:574-579.

[14]Liljeback P, Pettersen K, Stavdahl φ. Modelling and Control of Obstacle-Aided Snake Robot Locomotion Based on Jam Resolution[C]//2009 IEEE International Conference on Robotics and Automation.Kobe, Japan, 2009:3807-3814.

[15]Rincon D, Sotelo J. Dynamic and Experimental Analysis for Inchwormlike Biomimetic Robots[J]. IEEE Robotics& Automation Magazine, 2003: 53-57.

[16]Ma S, Tadokopo N. Analysis of Creeping Locomotion of a Snake-like Robot on a Slope[J]. Autonomous Robots, 2006, 20:15-23.

[17]李斌, 卢振利. 基于乐理的蛇形机器人控制方法研究[J]. 机器人, 2005, 27(1): 14-19.

Li Bin, Lu Zhenli. Control Method of a Snake-like Robot Based on Music Theory[J]. Robot, 2005, 27(1):13-19.

[18]张佳帆, 杨灿军, 陈鹰, 等. 蠕动式机器蛇的研究与开发[J].机械工程学报, 2005, 41(5):205-209.

Zhang Jiafan, Yang Canjun, Chen Ying, et al. Study and Develop of Snake-Robot with Concerpina-Locomotion[J]. Chese Journal of Mechanical Engineering, 2005, 41(5):2005-209.

[19]孙洪, 马培荪, 王光荣. 蛇形机器人一种基于Serpenoid 曲线的蠕动步态[J]. 机械设计与研究, 2008, 24(1):39-50.

Sun Hong, Ma Peisun, Wang Guangrong. An Inchworm Locomotion Gait Based on Serpenoid Curve for Snakelike Robot[J]. Machine Design and Research, 2008, 24(1):39-50.

[20]Chirikjian G. The Kinematics of Hyper-Redundant Robot Locomotion[J]. IEEE Transactions on Robotics and Automation, 1995, 11(6):781-793.

[21]Hatton R, Choset H. Sidewinding on Slopes[C]//2010 IEEE International Conference on Robotics and Automation.Anchorage, Alaska, 2010:691-696.

[22]Gong C, Hatton R, Choset H. Conical Sidewinding[C]//IEEE International Conference on Robotics and Automation.Saint Paul, Minnesota, 2012: 4222-4227.

[23]孙洪. 攀爬蛇形机器人的研究[D]. 上海: 上海交通大学, 2007.

[24]Date H, Hoshi Y, Sampei M. Locomotion Control of a Snake-like Robot Baesed on Dynamic Manipulability[C]//Proceedings of the 2000 IEEE/RSJ International Conference on Intelligent Robots and Systems.Takamatsu, 2000: 2236-2241.

[25]Prautsch P, Mita T. Control and Analysis of the Gait of Snake Robots[C]//Proceedings of the 1999 IEEE International Conference on Control Applications.Kohala Coast, HI, 1999: 502-507.

[26]Matsuno F, Sato H. Trajectory Tracking Control of Snake Robots Based on Dynamic Mode[C]//Proceedings of the 2005 IEEE International Conference on Robotics and Automation.Barcelona, Spain, 2005: 3029-3034.

[27]Li J, Shan J. Passivity Control of Underactuated Snake-like Robots[C]//Proceedings of the 7th World Congress on Intelligent Control and Automation.Chongqing, China, 2008: 485-490.

[28]Liljeback P, Pettersen K, Stavdahl φ. Controllability and Stability Analysis of Planar Snake Robot Locomotion[J]. IEEE Transactions on Automatic Control, 2011, 56(6): 1365-1380.

[29]Ma S, Ohmameuda Y, Inoue K, et al. Control of a 3-Dimensional Snake-like Robot[C]//Proceedings of the 2003 IEEE International conference on Robotics and Automation.Taipei, Taiwan, China,2003: 2067-2072.

[30]陈丽, 王越超, 马书根, 等. 蛇形机器人侧向运动的研究[J]. 机器人, 2003, 25(3):246-249.

Chen Li, Wang Chaoyue, Ma Shugen, et al.Study of Lateral Locomotion of Snake Robot[J]. Robot, 2003, 25(3): 246-249.

[31]魏武, 孙洪超. 蛇形机器人桥梁缆索攀爬步态控制研究[J]. 中国机械工程, 2012, 23(10): 1230-1236.

Wei Wu, Sun Hongchao. Research on Gait Generation and Control of Snake-like Robot for Bridge Cable Climbing[J]. China Mechanical Engineering, 2012, 23(10): 1230-1236.

[32]卢振利, 马书根, 李斌, 等. 基于循环抑制CPG模型的蛇形机器人控制器[J]. 机械工程学报, 2006, 42(5): 137-143.

Lu Zhenli, Ma Shugen, Li Bin, et al. Snake-like Robot Controller with Cyclic Inhibitory CPG Model[J]. Chinese Journal of Mechanical Engineering, 2006, 42(5): 137-143.

[33]卢振利, 马书根, 李斌, 等. 基于循环抑制CPG模型的蛇形机器人蜿蜒运动[J]. 自动化学报, 2006, 32(1): 132-139.

Lu Zhenli, Ma Shugen, Li Bin, et al. Serpentine Locomotion of a Snake-like Robot Controlled by Cyclic Inhibitory CPG Model[J]. ACTA Automatica Sinica, 2006, 32(1): 132-139.

[34]卢振利, 马书根, 李斌,等. 基于循环抑制CPG模型的蛇形机器人三维运动[J]. 自动化学报, 2007, 33(1): 54-58.

Lu Zhenli, Ma Shugen, Li Bin, et al. 3-dimensional Locomotion of a Snake-like Robot Controlled by Cyclic Inhibitory CPG Model[J]. ACTA Automatica Sinica, 2006, 32(1): 132-139.

[35]王智锋, 马书根, 李斌, 等. 基于能量的蛇形机器人蜿蜒运动控制方法的仿真和实验研究[J]. 自动化学报, 2011, 37(5): 604-613.

Wang Zhifeng, Ma Shugen, Li Bin, et al. Simulation and Experimental Study of an Energy-based Control Method for the Serpentine Locomotion of a Snake-like Robot[J]. ACTA Automatica Sinica, 2011, 37(5): 604-613.

[36]Wu X. Ma S. CPG-based Control of Serpentine Locomotion of a Snake-like Robot[J]. Mechatronics, 2010,20:326-334.

[37]Mori M, Hirose S. Three-dimensional Serpentine Motion and Lateral Rolling by Active Cord Mechanism ACM-R3[C]//Proceedings of the 2002 IEEE/RSJ International Conference on Intelligent Robots and Systems.Lausanne, Switzerland, 2002:829-834.

[38]Takaoka S, Yamada H, Hirose S. R4:2011Snake-like Active Wheel Robot ACM-R4.1 with Joint Torque Sensor and Limiter[C]//2011 IEEE/RSJ International Conference on Intelligent Robots and Systems.San Francisco, 2011: 1081-1086.

[39]Yamada H, Hirose S. Study of a 2-DOF Joint for the Small Active Cord Mechanism[C]//2009 IEEE International Conference on Robotics and Automation.Kobe, Japan, 2009:3827-3832.

[40]Worst R, Linnemann R. Construction and Operation of a Snake-like Robot[C]//IEEE International Joint Symposia on Intelligence and Systems.Rockville, MD, 1996: 164-169.

[41]Klaassen B, Paap K. GMD-Snake2: A Snake-Like Robot Driven by Wheels and a Method for Motion Control[C]//Proceedings of IEEE International Conference on Robotics and Automation.Detroit, MI, 1999: 3014-3019.

[42]Borenstein J, Borrell A. The OmniTread OT-4 Serpentine Robot[C]//2008 IEEE International Conference on Robotics and Automation.Pasadena,CA,2008:1766-1767.

[43]Gavin M. S5 Snake Robot Prototype[EB/OL]. 1999[2014-05-10]. http://www.snakerobots.com/

[44]Wright C, Buchan A, Brown B, et al. Design and Architecture of the Unified Modular Snake Robot[C]//2012 IEEE International Conference on Robotics and Automation (ICRA).Saint Paul, MN, 2012:4347-4354.

[45]Wright C, Johnson A, Peck A, et al. Design of a Modular Snake Robot[C]//Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems.San Diego, CA, 2007:2609-2614.

[46]McKenna J, Anhalt D, Frederick Bronson et al. Toroidal Skin Drive for Snake Robot Locomotion[C]//2008 IEEE International Conference on Robotics and Automation.Pasadena,CA, 2008:1150-1155.

[47]Liljeback P,Stavdahl φ, Beitnes A. Snake Fighter-Development of a Water Hydraulic Fire Fighting Snake Robot[C]//The 9th International Conference on Control, Automation, Robotics and Vision.Singapore,2006:1-6.

[48]PhysOrg.com. Robots, the Bizarre and the Beautiful[EB/OL]. (2009-09-29)[2014-05-10]. http://phys.org/news141921497.html.

[49]Transeth A, Liljeback P, Pettersen K. Snake Robot Obstacle Aided Locomotion: An Experimental Validation of a Non-smooth Modeling Approach[C]//Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems.San Diego, CA, 2007:2582-2589.

[50]Liljeback P, Pettersen K, Stavdahl φ. A Snake Robot with a Contact Force Measurement System for Obstacle-aided Locomotion[C]//2010 IEEE International Conference on Robotics and Automation.Anchorage, Alaska, 2010:683-690.

[51]叶长龙, 马书根, 李斌, 等. 三维蛇形机器人巡视者Ⅱ的开发[J]. 机械工程学报, 2009, 45(5): 128-133.

Ye Changlong, Ma Shugen, Li Bin, et al. Development of a Three Dimensional Snake-like Robot Rerambulator Ⅱ[J]. Journal of Mechanical Engineering, 2009, 45(5): 128-133.

[52]郁树梅, 王明辉, 马书根, 等. 水陆两栖蛇形机器人的研制及其陆地和水下步态[J]. 机械工程学报, 2012, 48(9): 18-25.

Yu Shumei, Wang Minghui, Ma Shugen, et al. Development of an Amphibious Snake-like Robot and Its Gait on Ground and in Water[J]. Journal of Mechanical Engineering, 2012, 48(9): 18-25.

[53]孙洪, 刘立祥, 马培荪. 一种新型的攀爬蛇形机器人[J]. 传动技术, 2008, 22(3):34-48.

Sun Hong, Liu Lixiang, Ma Peisun. A New Type Climbing Snake Robot[J]. Drive system Technique, 2008, 22(3):34-48.

[54]吉爱红, 戴振东, 周来水. 仿生机器人的研究进展[J]. 机器人, 2005, 27(3):284-288.

Ji Aihong, Dai Zhendong, Zhou Laishui. Research Development of Bio-inspired Robotics[J]. Robot, 2005, 27(3):284-288.

(编辑郭伟)

Present Situation and Development Tendency of Snake-like Robots

Su Zhong1,2Zhang Shuangbiao2Li Xingcheng2

1.Beijing Information Science & Technology University,Beijing,100101 2.Beijing Institute of Technology,Beijing,100081

A literature survey of researches on snake-likes was provided regarding morphology, modeling of kinematics and dynamics, locomotion control and stability. The analyses and summary were made according to the two-dimensional and three-dimensional locomotions. Classifications of snake-like robots were presented due to the differences of structures and movement types. Finally, the development of snake-like robots in future was predicted.

locomotion; kinematics; dynamics; control method; stability

2014-02-11

国家自然科学基金委员会及香港研究资助局联合科研基金资助项目(61261160497)；北京市科技计划项目(Z121100001612007)；北京市教委创新能力提升计划项目(PXM2013_014224_000093)

TP242DOI：10.3969/j.issn.1004-132X.2015.03.022

苏中，男，1962年生。北京信息科技大学通信学院院长、教授，北京理工大学自动化学院博士研究生导师，高动态导航技术北京市重点实验室主任。张双彪(通信作者)，男，1984年生。北京理工大学宇航学院博士研究生。李兴城，男，1969年生。北京理工大学宇航学院副研究员。