高中数学中的不等式恒成立问题

何 娟

（湖北省丹江口市第一中学 湖北十堰 442700）

高中数学中的不等式恒成立问题

何 娟

（湖北省丹江口市第一中学 湖北十堰 442700）

不等式恒成立问题是高考中的热点和难点，因其方法灵活多变，考察内容综合性强，学生在解决时往往难以入手，现将这类问题的常用方法总结一二。

构造函数 变换主元 分离参数 数形结合

不等式问题是数学中的重要内容之一，在数学的各个分支中都有广泛的应用，而含参数不等式恒成立问题又是重点中的难点。这类问题以含参不等式“恒成立”为载体，镶嵌函数、方程、不等式等内容，具有一定的综合性和复杂性，因而成为近几年高考试题中的热点。在确定恒成立不等式中参数的取值范围时，需要在函数思想的指引下，灵活地进行代数变形、综合地运用多科知识。其解法多变，思维含量较高，渗透了函数与方程、数形结合、转化与化归等一系列数学思想方法。本文将通过实例，从不同角度用常规方法归纳，就其常见类型及解题策略举例说明，理解不等式证明的数学思想与使用策略，体会数学的科学价值和实用价值。

一、构造函数法

函数是高中数学中一颗美丽的明珠，很多数学问题都可以应用函数来解决。在解决不等式恒成立问题时，即可通过构造适当的函数，然后利用相关函数的图象和性质解决问题。

点评：对此类含参问题，若所构造函数较复杂时，可从特殊值入手，初步缩小变量的取值范围，可有效减少后续工作量，解题目中要注意该技巧的使用。

二、变换主元法

在一个含多个变量的数学问题中，需要确定合适的变量和参数，从而揭示函数关系，使问题本质更加清晰明了，一般来说，已知范围的量视为变量，而待求范围的量视为参数。

例1：对任意m∈［-1,1］，不等式x2+mx+1≥3恒成立，求实数x的取值范围。

分析：题中已知m的范围，故可视y=x2+mx +1为m的一次函数。

解：令g( m)=mx+x2+1，因是一次函数，相应的直线斜率为x

当x＞0时，g( m)为递增函数，要使g( m)≥3，必须满足g(-1)≥3

即g(-1)=x2-x +1≥3，解得x≥2；

当x＜0时，g( m)为递减函数，要使g( m)≥3，必须满足g(1)≥3

即g(1)=x2+x+1≥ 3，解得x≥-2；

当x=0时，g( m)=1≤3，不符合要求，舍去。

则，x的取值范围为｛x| x≤-2或x≥2｝。

此问题常因思维定势，学生易把它看成关于x的不等式讨论，从而因计算繁琐出错或者中途夭折；若转换一下思路，把待求的x为参数，以m为变量，则问题转化为求一次函数（或常数函数）在给定区间上求最值，再来求解参数x应满足的条件，这样问题就轻而易举的得到解决了。一般地，在求解“含参不等式恒成立问题”时，遵循“已知谁的范围，则视为谁的函数”，可帮助我们快速确定构造函数的方向。将恒成立问题转化为求函数最值问题。

三、分离参数法

所谓分离参数法，就是将参数与未知量分离于不等式的两边，然后根据未知量的取值情况，通过求函数最值的方法来确定参数的取值范围。在不等式中求参数范围时，当参数较易分离，且分离后不等式一边的函数（或代数式）的最值或范围可求时，常用分离参数法。

此类问题把要求的参变量分离出来，单独放在不等式的一侧，将另一侧看成新函数，于是将问题转化成新函数的最值问题。若对于x取值范围内的任一个数都有恒成立，则；若对于x取值范围内的任一个数都有恒成立，则.当求解时，所求变量的系数容易确定范围，变量容易分离出来时，可将变量分离后转化为求一个不含变量的新函数的最值问题.

四、数形结合法

数形结合法，就是先把不等式或经过变形的不等式两端分别看成两个函数，再画出两函数的图象，然后通过观察两图象（特别是交点时）的位置关系，最后列出含参数不等式恒成立问题中的参数范围。

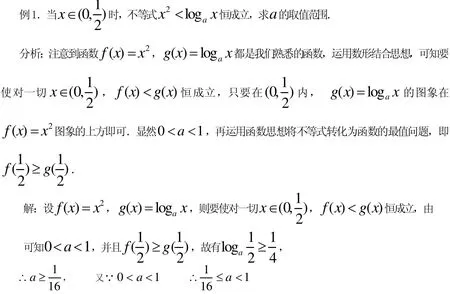
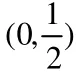
我们一起来看看下面一道题目：（2006年，上海卷，理12）三个同学对问题“关于x的等式在［1,12］上恒成立，求实数a的取值范围”提出各自的解题思路。

甲说：“只须不等式左边的最小值不小于右边的最大值”

乙说：“把不等式变形为左边含变量x的函数，右边仅为常数，求函数的最值”

丙说：“把不等式两边看成关于x的函数，作出函数的图象”

参考上述解题思路，你认为他们所讨论的问题的正确讨论，即a的取值范围为————

笔者认为这是不等式恒成立问题中非常经典的一个题目，甲的观点是一个非常典型的错误，是很多学生都在此处容易出错的。题目要的是f（x）>g（x）处处成立，而与f（x）与g（x）的最值完全没有关系；丙的想法理论上没问题，但对于我们而言，左边的这个函数图象我们根本无法作出，属于理论上可行但实际不可操作；乙的思路完全正确，正是此题的完美解法。由此，我们一起来探讨两类问题：

1. f( x)＞g( x)型不等式

这类问题往往转化成不等式 f( x)-g( x)＞0，转而求左边新函数的最值。

例. 已知函数f( x)=ex,直线l的方程为y=kx+b.

点评：此类形如f（x）>g（x）不等式问题模式性非常强，一般可按如下步骤解决

①构造函数h（x）=f（x）-g（x）

②研究h（x）单调性求最值

③利用不等式性质求解

2. f( x1)＞g( x2)型不等式

这类问题不等号左，右两边变量不同，所以两边函数取值不影响，在解决这种问题时可转化为求两个函数的最值问题。

不等式是数学史上的一座不朽的丰碑，而不等式的恒成立问题又是丰碑上最璀灿的明珠。含参数的不等式恒成立问题往往与函数的单调性、极值、最值等有关，所以解题时要善于将这类问题与函数联系起来，通过函数最值求解相关问题，渗透函数思想，在应用中体会数学的无究魅力。

［1］田宝运.不等式问题中的数学思想［J］.中学数学研究

［2］郭希连.不等式的解法［J］.数学通讯，

［3］楼伯寿.含参数不等式的解法之数形结合［J］.中学教研，

［4］孟凡栋.《恒成立类型不等式中参数范围的几种求法》.《数学教学通讯》