复杂载荷条件下有缺陷海底管道非线性屈曲分析

陈飞宇，余建星，赵羿羽，孙震洲，刘见德



复杂载荷条件下有缺陷海底管道非线性屈曲分析

陈飞宇，余建星，赵羿羽，孙震洲，刘见德

(天津大学水利工程仿真与安全国家重点实验室，天津，300072)

针对有初始缺陷海底管道在弯曲、轴力和外部静水压力联合作用下的复杂载荷屈曲压溃问题，建立管道的屈曲压溃理论模型，研究中考虑管道变形的几何非线性和材料非线性，运用结构弹塑性本构关系，基于虚功原理建立管道屈曲压溃方程；运用MATLAB编程进行数值计算，分别研究分析弯曲、轴力和外部静水压力单独作用，以及3种载荷联合作用的管道压溃压力。研究结果表明：复杂载荷条件下的有缺陷管道，尤其是当轴力和曲率比较大时，各因素对管道屈曲压溃压力影响的非线性特征逐渐明显；多种载荷的联合作用与单一载荷对屈曲压溃压力的影响是不一致的。研究结果可为实际工程中海底管道临界屈曲载荷的确定、危险位置的辨识、设计中的结构参数优化以及施工中的屈曲控制提供理论依据，从而保障海洋油气输送安全。

海底管道；复杂载荷；屈曲压溃；非线性；压溃压力

海底油气管道在生产制造过程中，其几何尺寸和材料性质分布存在一定程度的不均匀性，使管道存在初始缺陷；管道在铺设和使用过程中，如果发生碰撞或腐蚀等现象，会进一步加重管道缺陷，这些缺陷会大大降低管道抵抗屈曲压溃的能力。另外，海底管道在其全寿命周期内始终承受外部静水压力、弯曲和轴力作用，而这些载荷联合作用所造成的复杂载荷条件会让管道具有更高的屈曲压溃风险。国外学者对管道屈曲压溃问题的研究开展较早。Yeh等[1−3]提出了二维圆环和三维圆柱壳理论模型，对管道在静水压力作用下的屈曲压溃进行了理论分析；Tokimasa等[4−5]对管道屈曲压溃问题进行了数值模拟和相关试验；Shaw 等[6]基于虚功原理的理论分析模型，研究了管道在循环弯矩作用下的变形响应；之后，国外学者们进一步研究了管道在弯矩与轴力联合作用[7]、弯矩与外压联合作用[8−9]以及轴力与外压联合作用[10−11]下的屈曲压溃问题。在国内，陈铁云等[12]对不同几何尺度的加筋圆柱壳在外部静水压力作用下的屈曲问题进行了试验和理论研究；龚顺风等[13]对外部高静水压力作用下的有初始缺陷厚壁管道进行了模型试验和有限元数值模拟；张日曦等[14]基于经典理论和数值模拟结果得到了适用于小径厚比深水管道屈曲压溃分析的临界压力修正公式；余建星等[15−16]运用有限元数值模拟和圆环理论模型研究了有缺陷海底管道在外部水压作用下的屈曲压溃问题，并与全比例管件试验结果进行了对比分析。通过以上分析可以看出：国内学者对管道屈曲压溃问题的分析一般仅针对外部静水压力作用，研究方法一般采用有限元数值模拟和试验，而对理论的研究与国外存在较大差距，特别是考虑复杂载荷的联合作用。基于以上考虑，本文作者针对有缺陷海底管道在弯曲、轴力和外部静水压力联合作用下的复杂载荷屈曲压溃问题进行理论研究，研究中考虑了管道变形的几何非线性和材料非线性，运用了结构弹塑性本构关系，基于虚功原理建立了管道屈曲压溃方程；然后运用MATLAB编程进行数值计算，研究分析了复杂载荷条件下弯曲、轴力、外压对管道屈曲压溃压力的影响。

1 理论模型

管道在外压作用下会发生椭圆度变形。对于沿轴向具有缺陷程度近乎相同的较长管道而言，在其前屈曲阶段，这种椭圆度变形沿轴向几乎是一致的，直至缺陷程度略大于其他截面的部位首先发生屈曲失稳为止。管道压溃压力的确定，与失稳之后的后屈曲阶段无关，仅取决于轴向变形一致的前屈曲阶段，可以以某一截面的变形代替管道整体的变形。管道的弯曲类似于梁的弯曲，横截面受弯曲而变形后仍然为平面。基于以上原因作出如下假定：

1) 管道轴向应变和环向应变沿管壁厚度方向满足直法线假定条件，管壁变形满足平断面假定条件；

2) 径向应变与环向应变相比很小，忽略不计；

3) 管道变形过程中，材料保持各向同性；

4) 仅考虑管道初始椭圆度几何缺陷，且缺陷沿轴向分布相同；

5) 加载过程中忽略加载路径的影响。

基于以上假定，建立管道在弯曲、轴力和外压联合作用下的复杂载荷条件屈曲压溃理论模型如图1 所示。

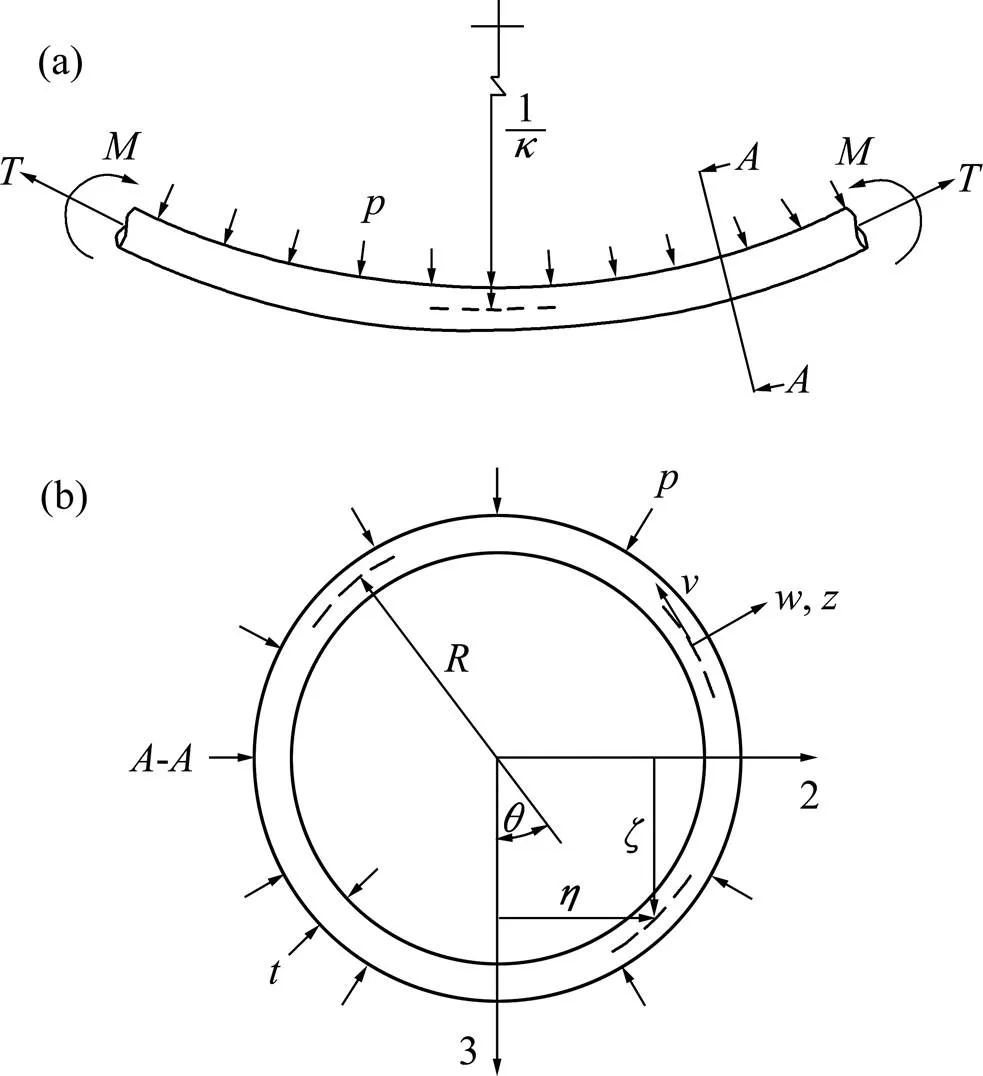
(a) 管道径向受力示意图；(b) 管道横向受力示意图

图1中，表示内外压差；表示轴力；表示弯矩；表示曲率；表示管道壁厚；表示管壁中性层半径；表示中性层法向坐标；和分别为中性层处质点的环向位移和径向位移，用以表征管道变形和应变关系；和分别为中性层处某质点的横纵坐标，该点与纵轴的夹角为，用以表征管道的空间形状变化。质点的位移和坐标关系为：

(2)

1.1 几何方程

(4)

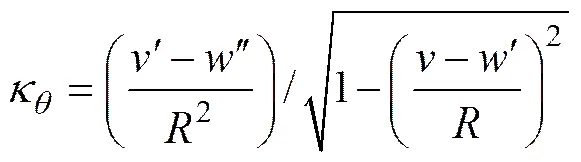
(6)

1.2 本构方程

考虑管道屈曲过程中的大变形，管道会进入弹塑性变形阶段，因此，本构关系采用J2塑性流动理论[17]，即

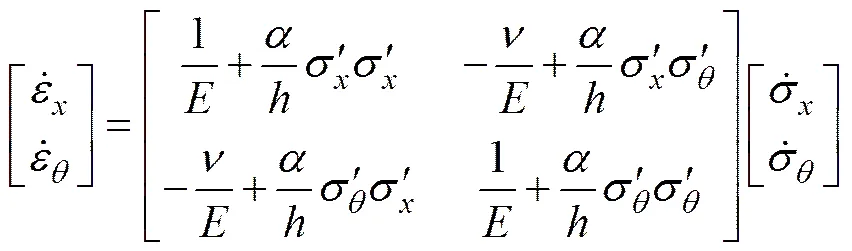
1.3 能量方程

管道在弯曲、轴力和外部静水压力联合作用下，由虚功原理可得平衡方程为[18]

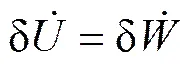
(10)

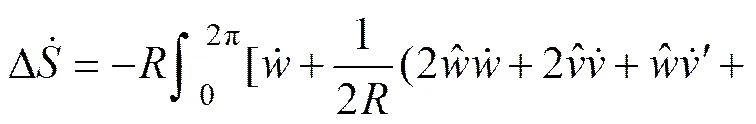
(11)

2 方程求解

2.1 方程的离散

设管道屈曲为椭圆化屈曲，则位移和可离散为如下级数形式：

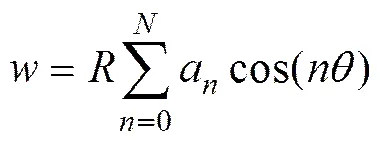
式中：a和b分别为位移函数中的待求参数。

设管道具有初始椭圆度缺陷：

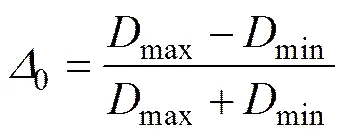
其中：max和min分别为管道椭圆横截面的最大直径和最小直径。

初始椭圆度的形状函数为

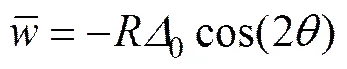
2.2 非线性方程组的建立

将式(2)代入式(6)，可得轴向应变增量的变分为

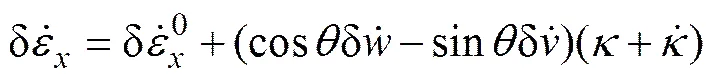
由式(3)可得环向应变增量的变分为

(16)

由式(4)和式(5)可得薄膜应变增量的变分和弯曲应变增量的变分分别为

(17)

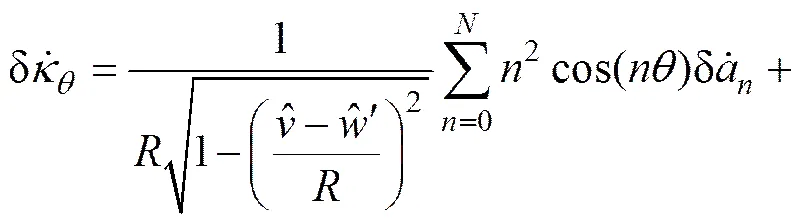
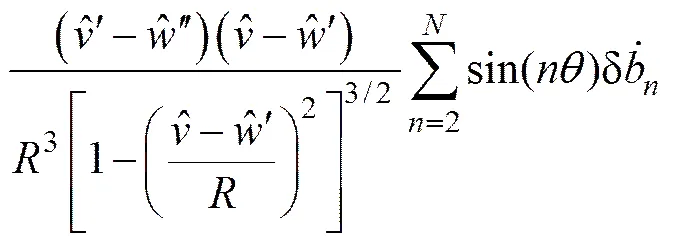
将式(15)代入式(10)，可得：

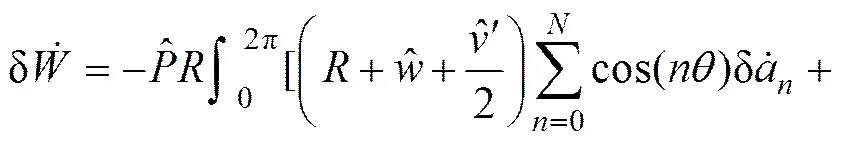
(19)

将式(15)，(16)和(19)代入式(8)，由方程等式恒成立，可得如下平衡方程：

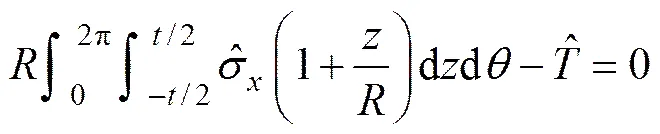
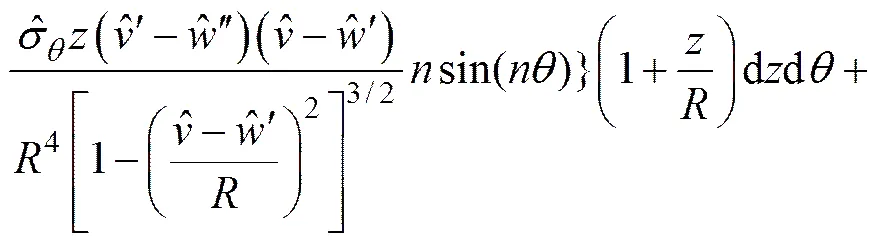
(21)

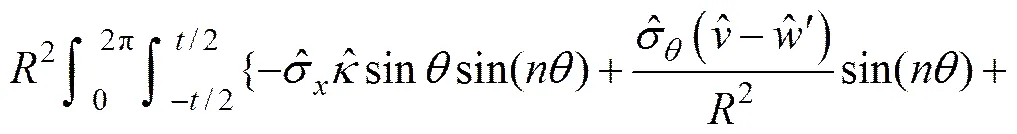
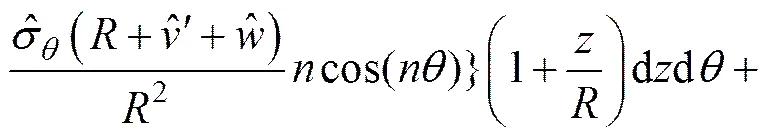
(22)

3 算例分析

以材料为API 5L X65的管道为例，弹性模量= 2.06×1011Pa，屈服极限448 MPa，管道直径为325 mm，壁厚为10 mm。

3.1 管道弹塑性弯曲分析

图2所示为初始椭圆度0.25%的管道弯矩作用下承载能力随曲率的变化曲线。从图2可以看出：弯矩承载力早期与曲率呈线性关系，之后弯矩承载力的非线性特征逐渐明显，并随曲率的增加而趋于平缓，直至达到最大值。因此，管道的曲率必须控制在管道发生弯曲屈曲之前；同时，在复杂载荷条件下的管道屈曲压溃分析中，曲率应在弯矩承载力达到最大值以前取值。

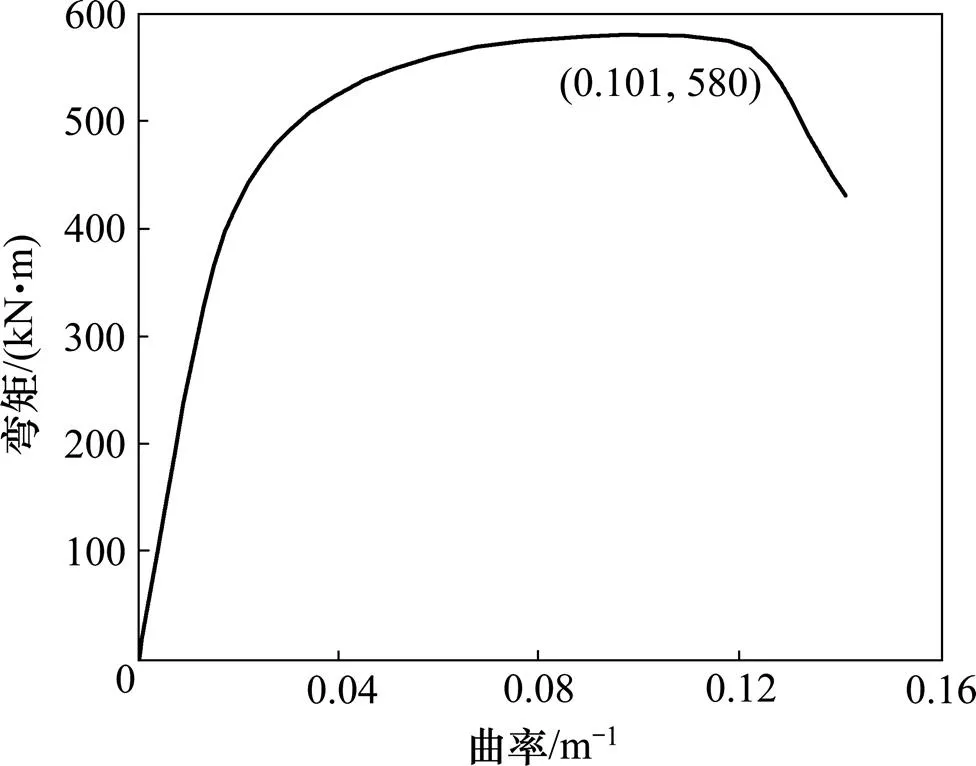
图2 弯矩−曲率关系曲线

3.2 弯曲对管道屈曲压溃压力的影响

图3所示为不同初始椭圆度管道在不同曲率下的屈曲压溃压力。从图3可以看出：弯曲(曲率)对屈曲承载能力的减弱作用十分显著，屈曲压溃压力随曲率的增加而大幅降低；此外，较大弯曲也使管道截面发生严重椭圆化，因此，随着曲率的增加，初始椭圆度对屈曲压溃压力所造成的差异逐渐缩小。

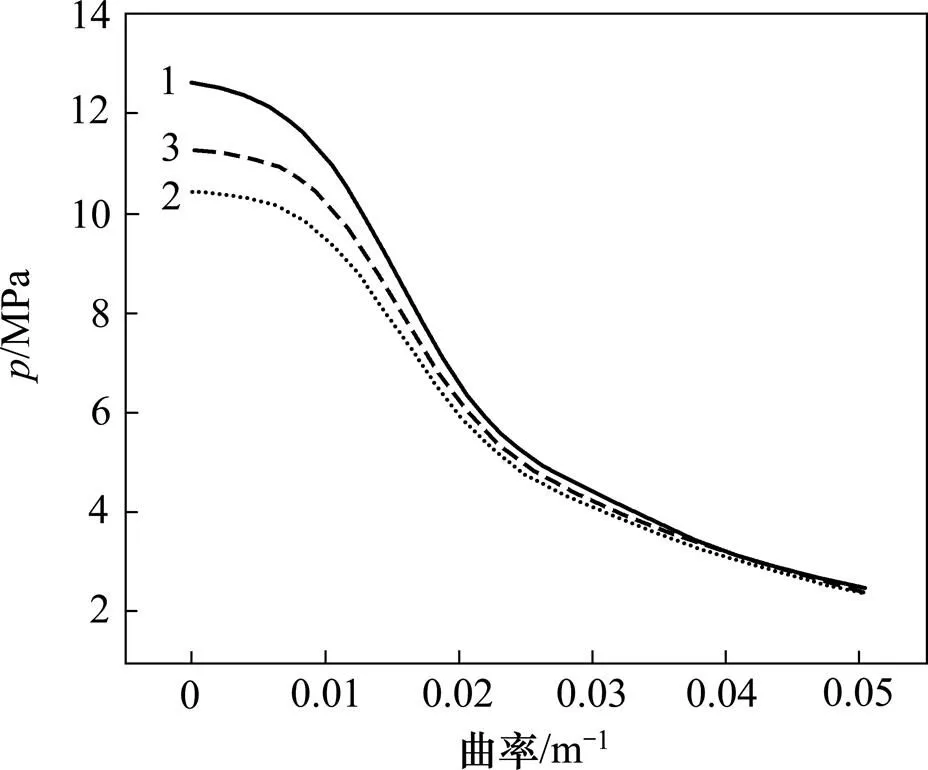
椭圆度/%：1—0.10; 2—0.30; 3—0.50

3.3 轴力对管道屈曲压溃压力的影响

图4所示为初始椭圆度0.25%的管道屈曲压溃压力随轴力的变化曲线(0为屈服轴力)。从图4可以看出：当轴力较小时，轴力对管道屈曲压溃压力的影响不大，但随着轴力增加，其影响程度快速加剧。因此，对于管道屈曲压溃而言，必须根据实际情况将轴力控制在一定范围内，超出该范围管道将面临严重的屈曲压溃危险。

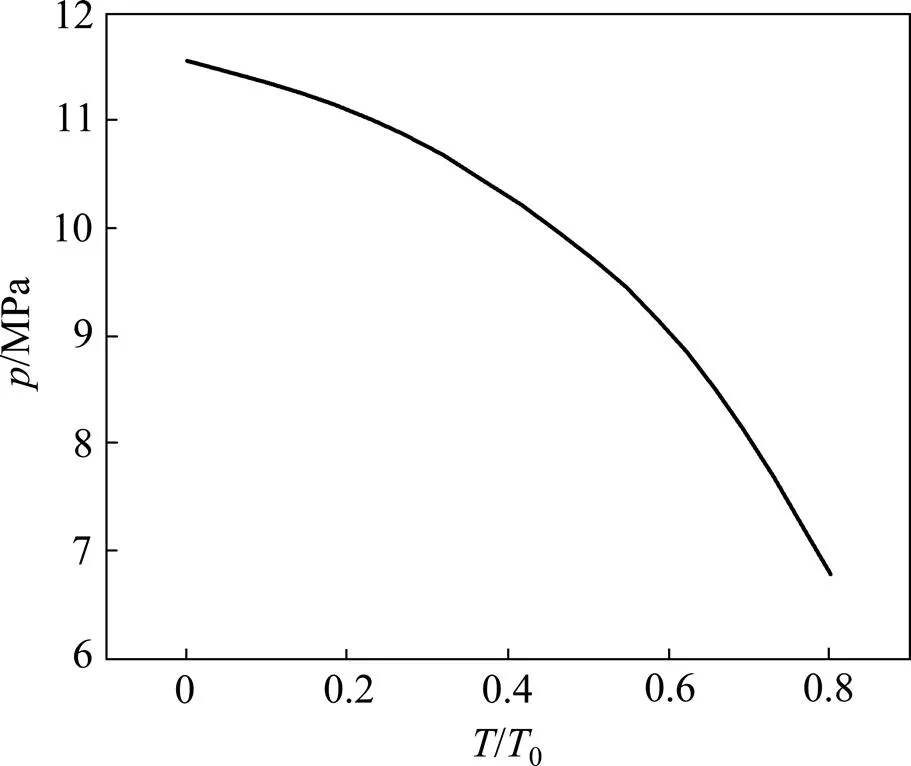
图4 屈曲压溃压力−轴力关系曲线

3.4 弯曲、轴力和外压联合作用下的管道屈曲压溃

图5所示为初始椭圆度0.10%的管道在弯曲(曲率)、轴力和外压联合作用下的屈曲压溃压力变化曲线。从图5可以看出：对于复杂载荷条件下的有缺陷管道，尤其是当轴力和曲率比较大时，各因素对管道屈曲压溃压力影响的非线性特征逐渐明显；通过与图3和图4对比发现，多种载荷的联合作用与单一载荷对屈曲压溃压力的影响规律是不一致的。

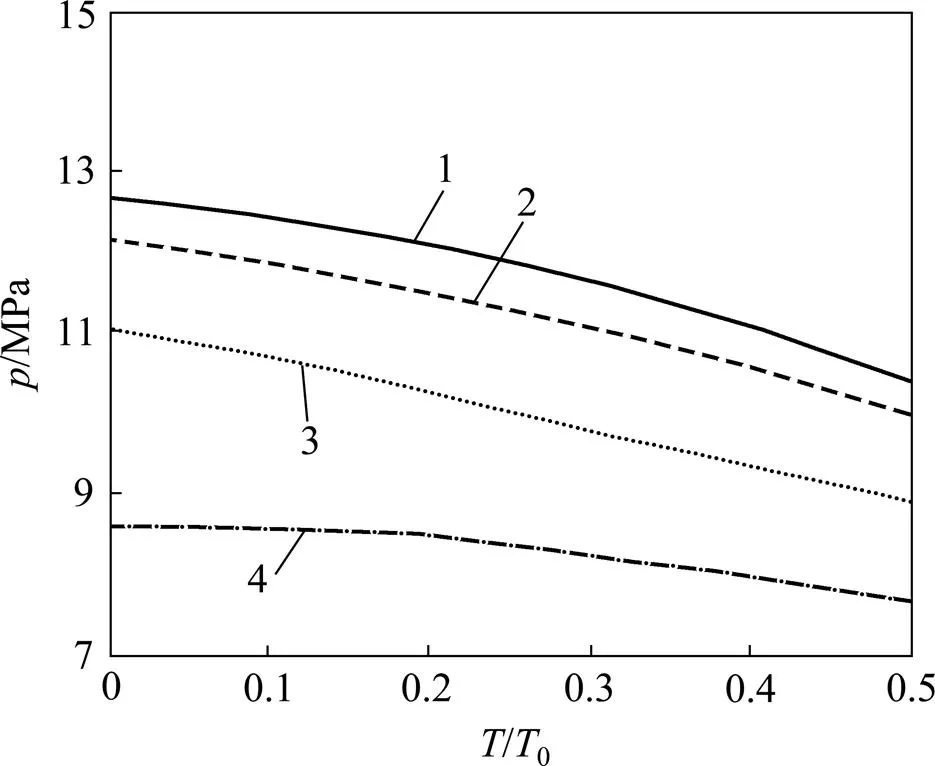
曲率/m−1：1—0; 2—0.005; 3—0.010; 4—0.015

4 结论

1) 通过建立管道屈曲压溃理论模型，对有初始椭圆度缺陷的海底管道在弯曲、轴力和外压联合作用下的复杂载荷屈曲压溃问题进行了理论推导，并进行了编程计算，对不同载荷组合下的管道屈曲压溃压力进行了分析研究。

2) 弯曲(曲率)载荷对于管道屈曲十分重要，既要防止曲率达到一定程度所造成的弯曲失稳，又要充分考虑曲率对管道屈曲压溃承载能力的影响；对于管道铺设过程中的悬垂段、海底管道悬跨段以及整体屈曲所导致的侧弯等实际情况，应根据所处水深的外部静水压力，设法将管道曲率控制在安全范围内。

3) 轴力对管道屈曲压溃的影响表现出明显的非线性特征，在小轴力范围内影响较小，但随轴力的增加，其影响程度迅速加剧。在实际工程中，应依据可能发生的复杂工况，对管道弯曲和轴力的载荷组合形式进行合理控制，以保障海底管道的结构安全。

参考文献：

[1] Yeh M K, Kyriakides S. On the collapse of inelastic thick-walled tubes under external pressure[J]. Journal of Energy Resources Technology, 1986, 108(1): 35−47.

[2] Yeh M K, Kyriakides S. Collapse of deepwater pipelines[J]. Journal of Energy Resources Technology, 1988, 110(1): 1−11.

[3] Dyau J Y, Kyriakides S. On the localization and collapse in cylindrical shells under external pressure[J]. International Journal of Solids and Structures, 1993, 30(4): 463−482.

[4] Tokimasa K, Tanaka K. FEM analysis of collapse strength of a tube[J]. Journal of Pressure Vessel Technology, 1986, 108(2): 158−164.

[5] Assanelli A P, Toscano R G, Johnson D H, et al. Experimental/numerical analysis of the collapse behavior of steel pipes[J]. Engineering Computations, 2000, 17(4): 459−486.

[6] Shaw P K, Kyriakides S. Inelastic analysis of thin-walled tubes under cyclic bending[J]. International Journal of Solids and Structures, 1985, 21(11): 1073−1100.

[7] Dyau J Y, Kyriakides S. On the response of elastic-plastic tubes under combined bending and tension[J]. Journal of Offshore Mechanics and Arctic Engineering, 1992, 114(1): 50−62.

[8] Corona E, Kyriakides S. On the collapse of inelastic tubes under combined bending and pressure[J]. International Journal of Solids and Structures, 1988, 24(5): 505−535.

[9] Corona E, Kyriakides S. Asymmetric collapse modes of pipes under combined bending and external pressure[J]. Journal of Engineering Mechanics, 2000, 126(12): 1232−1239.

[10] Tamano T, Mimura H, Yanagimoto S, et al. Examination of commercial casing collapse strength under axial loading[J]. Journal of Energy Resources Technology, 1982, 104(4): 343−348.

[11] Madhavan R, Babcock C D, Singer J. On the collapse of long, thick-walled tubes under external pressure and axial tension[J]. Journal of Pressure Vessel Technology, 1993, 115(1): 15−26.

[12] 陈铁云, 邵文蛟. 加环肋圆筒形薄壳在静水外压下的总体大挠度塑性稳定性及初挠度对其影响[J].中国造船, 1979(3): 59−78. CHEN Tieyun, SHAO Wenjiao. The general plastic stability theory of ring-stiffened cylindrical shells with large deflection under external hydrostatic pressure and the influence of initial imperfections on their instability[J]. Ship Building of China, 1979(3): 59−78.

[13] 龚顺风, 陈源, 金伟良, 等. 高静水压力作用下深海油气管道的局部屈曲[J]. 浙江大学学报(工学版), 2012, 46(1): 14−19. GONG Shunfeng, CHEN Yuan, JIN Weiliang, et al. Local buckling of deeowater oil-gas pipeline under high hydrostatic pressure[J]. Journal of Zhejiang University (Engineering Science), 2012, 46(1): 14−19.

[14] 张日曦, 张崎, 黄一. 小径厚比深水管道的压溃屈曲研究[J]. 船舶工程, 2012, 34(4): 94−97. ZHANG Rixi, ZHANG Qi, HUANG Yi. Collapse buckling study on deepwater pipelines with small radius-thickness ratio[J]. Ship Engineering, 2012, 34(4): 94−97.

[15] 余建星, 卞雪航, 余杨, 等. 深水海底管道全尺寸压溃试验及数值模拟[J]. 天津大学学报, 2012, 45(2): 154−159. YU Jianxing, BIAN Xuehang, YU Yang, et al. Full-scale collapse test and numerical simulation of deepwater pipeline[J]. Journal of Tianjin University, 2012, 45(2): 154−159.

[16] 余建星, 李智博, 杜尊峰, 等.深海管道非线性屈曲理论计算方法[J]. 海洋工程, 2013, 31(1): 54−60. YU Jianxing, LI Zhibo, DU Zunfeng, et al. Theoretical calculation method of the nolinear buckling of deepsea pipes[J]. The Ocean Engineering, 2013, 31(1): 54−60.

[17] 黄克智, 黄永刚. 固体本构关系[M]. 北京: 清华大学出版社, 1999: 14−35. HUANG Kezhi, HUANG Yonggang. The constitutive relation of solid[M]. Beijing: Tsinghua University Press, 1999: 14−35.

[18] Kyriakide S, Corona E. Mechanics of offshore pipelines (Volumn Ⅰ: Buckling and collapse)[M]. Oxford: Elsevier Science Ltd, 2007: 225−235.

Nonlinear buckling of subsea pipes with imperfection under complex loads

CHEN Feiyu, YU Jianxing, ZHAO Yiyu, SUN Zhenzhou, LIU Jiande

(State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China)

In order to study the buckling collapse of subsea pipes with initial imperfection under the complex loads including bending, axial force and external hydrostatic pressure, a theoretical model of pipe‘s buckling was established. Considering the geometric and material nonlinearity in pipe’s deformation, utilizing the structural elastic-plastic constitutive relation, the pipe’s buckling equation was derived based on the principle of virtual work. According to the MATLAB programming, the collapse pressures of the pipe were calculated under the bending, axial force or external hydrostatic pressure, and under the combined effect of the three loads, respectively. The results show that for the pipe with initial imperfection under complex loading condition, especially when the axial force and curvature are large, the loading impact on the pipeline buckling collapse presents nonlinear characteristic. And the influences of complex loads and single load are different. The research results can provide a theoretical foundation for the determination of critical buckling load, identification of hazardous location, design in the structural parameter optimization and buckling control in actual construction, thereby guaranteeing the safety of offshore oil and gas transport.

subsea pipe; complex loads; buckling collapse; nonlinear; collapse pressure

10.11817/j.issn.1672-7207.2015.07.043

P756.2

A

1672−7207(2015)07−2701−06

2014−08−21；

2014−10−22

国家重点基础研究发展规划(973计划)项目(2014CB046803)；国家自然科学基金资助项目(51239008)；天津科委资助项目(Z14SJENG0060)；国家科技重大专项项目(2011ZX05030-006) (Project(2014CB046803) supported by the National Basic Research Development Program of China (973 Program); Project(51239008) supported by the National Natural Science Foundation of China; Project(Z14SJENG0060) supported by the Science and Technology Commission of Tianjin; Project(2011ZX05030-006) supported by the National Science and Technology Major Project)

赵羿羽，博士研究生，从事海洋工程风险评估、海底管道屈曲分析研究；E-mail: zhaoyiyu1990@126.com

(编辑 杨幼平)