基于PFC3D单轴压缩下含2条裂隙试样力学行为的数值分析

范祥，曹平



基于PFC3D单轴压缩下含2条裂隙试样力学行为的数值分析

范祥1, 2，曹平1

(1. 中南大学资源与安全工程学院，湖南长沙，410083；2. 长安大学公路学院，陕西西安，710064)

基于离散元数值分析软件PFC3D中的颗粒接触黏结模型，以校核试验数据的方式获得数值模型的细观参数，进一步建立含有2条裂隙的数值计算模型，分别设定岩桥倾角为15°，30°，45°，60°，75°和90°。研究岩桥倾角对裂隙试样的峰值强度、起裂应力、峰值强度时刻轴向应变、弹性模量和破坏模式的影响。研究结果表明：岩桥倾角对含2条裂隙试样弹性模量的变化影响极小，但对峰值强度和起裂应力具有较大影响；随岩桥倾角的变化，裂隙试样单轴抗压强度与起裂应力有相似的变化关系，岩桥倾角影响裂隙试样在峰值应力时的应变。另外，岩桥倾角影响单轴荷载下裂纹的扩展方式，60°岩桥最容易贯通，15°和90°岩桥最难贯通。

数值模拟；PFC3D；裂隙；岩桥；裂纹扩展

岩体中各种裂隙的存在导致了岩石材料各向异性和强度性质的弱化，而裂隙岩体的强度对交通隧道、采矿硐室和巷道等岩体工程具有较大影响。因此，裂隙岩体力学性质一直是岩石力学界关注的焦点问题。对于裂隙岩体力学行为的研究，通常是人为制作含有裂隙的类岩试样，通过室内试验设备加载，测试其强度与变形特征，以及采用高速摄像设备观察裂纹扩展路径。石膏、水泥与细砂混合物是常用的类岩材料，陈新等[1−2]以石膏制作含有多条裂隙的类岩试样，研究单轴荷载下节理倾角、连通率对岩体强度和变形特征的影响，以及单轴荷载所致裂隙岩体的破碎规律。黎立云等[3]采用高强度白水泥和石膏作为类岩材料制作有序多裂纹试样，着重研究了宏观力学参数受裂纹密度的影响。蒲成志等[4−5]以水泥和细砂为类岩材料，研究了2条预制裂隙试样在单轴荷载下，裂隙倾角与岩桥倾角组合对裂纹扩展以及岩体破坏规律的影响。试验方法能够直接得到试样强度和变形参数，以及观察到裂纹扩展路径，但是试样可重复性差且制作耗费时间，有时数据离散性偏大。数值模拟是重现裂隙岩体受压裂纹扩展、强度变化的一种好方法。基于不同理论的多种数值分析软件已应用于裂隙岩体力学行为的模拟，Lee等[6]运用3种不同材料，制作含有预制裂纹的类岩试样，研究了单轴压缩荷载效应下裂纹的起裂、扩展与合并，再运用PFC2D建立数值试验模型，数值模拟结果与试验结果显示出了良好的吻合。Kulatilake等[7]以断裂张量描述了给定方向节理几何参数(节理密度、方向、大小分布和节理组数)的方向效应，再运用PFC3D校核试验数据，数值模拟和试验结果显示节理岩块的抗压强度随断裂张量增加呈非线性下降，节理几何参数控制着岩块的破坏模式。蒲成志等[5, 8]运用有限差分软件FLAC3D，在试验数据的基础上，建立应变软化模型，探索裂隙倾角与分布密度对岩体强度弱化的影响，所发现的规律可为预测裂隙围岩强度的变化提供参考。唐春安等[9−11]运用RFPA2D研究了岩石非均质性对裂纹扩展及峰值强度的影响，发现非均质度越差，材料的破坏峰值强度越低，且非均质岩体裂纹呈弥散分布。在荷载作用下，裂隙岩体裂纹扩展方式直接影响裂隙岩体的破坏模式，因此，研究者一直关注着裂纹的萌生和扩展方式，试验者通常会采用高速摄像机拍摄加载过程中裂纹的扩展过程。Wong等[12]在对含有2条裂隙，且裂隙倾角和岩桥倾角变化的试样加载过程中，观察到3种裂纹合并方式：剪切型，翼型拉伸型和拉剪混合型，Kulatilake等[7]也发现裂隙岩体有此3种破坏模式。蒲成志等[4]在分析2条预制裂隙试样压缩破坏时，发现有的试样由单一裂隙尖端起裂、扩展导致破坏，有的试样由2条裂隙搭接、贯通导致破坏，第2种破坏方式显得更为复杂。Wong等[13]在对单轴荷载下石膏和大理岩含有2条预制裂隙试样分析后，提出了9种裂纹扩展、合并模式，并指出裂纹的扩展方式与裂隙倾角、岩桥倾角及2条裂隙间长度有关。Fan等[14]基于试验数据，建立了不同倾角的多裂隙颗粒流模型，用数值模拟方法再现了试验中观察到的破坏模式。本文作者基于PFC3D中接触黏结模型，以校核试验数据的方式，建立裂隙岩体数值计算模型，从数值模拟角度分析岩桥倾角对裂隙岩体强度与变形性质的影响，以及单轴压缩效应下裂纹的萌生、扩展过程。

1 完整试样校核与裂隙数值模型的建立

1.1 试验简介

本文选取的试验数据源于文献[4]。在文献[4]中，采用水泥、水和细砂，按照体积比为2:1:1制成长×高×厚为150 mm×200 mm×30 mm的完整类岩试样(见图1)，经过室内养护后，采用高精度微机控制电液伺服万能试验机进行加载试验，其加载速率为200 N/s，得到的完整类岩试样物理参数如表1所示。

图1 试样尺寸示意图

表1完整类岩试样单轴压缩下物理力学参数[4]

1.2 完整试样校核

接触黏结(contact bond)是PFC中颗粒黏结的一种基本方式，接触黏结不能抵抗弯矩，只能承受法向力和切向力。当法向或切向中任一方向承受的力超过其设定强度时，接触黏结即被破坏，且剪切强度不依赖于法向力的大小。本文选用接触黏结方式，接触黏结模型主要由5个细观参数控制其力学行为，颗粒接触弹性模量、颗粒刚度比、颗粒间摩擦因数、接触黏结法向强度和切向强度。不同的参数影响试样的不同宏观物理性质，如颗粒接触弹性模量与试样弹性模量和峰值强度直接相关、接触黏结强度直接影响试样的宏观强度，相关说明参考PFC3D使用手册[15]。

事实上，单轴压缩下试样厚度(沿方向)一定程度减少对试样宏观参数的影响不会太大，当试样厚度减少1/3时，其单轴抗压强度和弹性模量降低一般在10%以内。考虑到数值计算时间与计算机性能，为了建立更加精细的数值分析模型，本文设定数值分析模型厚度为试验试样厚度的2/3，其余两边尺寸保持相同。根据表2中的参数，建立了含有96 833个球形颗粒和481 084个接触黏结的数值分析模型(见图2(a))。图2(a)中颗粒就是组成数值模型的基本单元。由于本模型中颗粒较多，接触力分布比较密集，难于分辨。图2(b)所示为经过放大后截取部分试样颗粒之间的接触力分布，线条的粗细表示接触力的大小。

表2 数值模型采用的细观参数

(a) 数值模型；(b) 接触力分布图

根据不同细观参数的作用，经过多次调整模型中细观参数值，发现当采用表2中的细观参数时，得到的完整试样宏观参数(见表3)与试验结果(见表1)吻合良好。单轴抗压强度和弹性模量之间的相对误差均在1%以内，因此，采用表2中的细观参数建立完整试样数值模型。

表3 数值模型宏观参数

1.3 裂隙模型的建立

基于软件手册的表述，这里所说节理即为裂隙。文献[4]中，设定2条在方向上贯通的裂隙，为裂隙倾角，为岩桥倾角，单条裂隙长度为20 mm，岩桥长度为40 mm。在此基础上，为了研究岩桥倾角对裂纹扩展的影响，本文确定裂隙倾角为45°，岩桥倾角分别为15°，30°，45°，60°，75°和90°。PFC3D数值分析模型中节理平面由倾向、倾角限定其方向，并可通过控制其在，和方向的长度来生成有限长度节理。通过降低与节理面相接触颗粒的细观参数值，来弱化节理的力学性质。通常，与节理面相接触的颗粒黏结强度设定为0，其摩擦因数也小于其他颗粒摩擦因数，颗粒刚度也应小于其他颗粒刚度。

图3所示为含有2条节理的数值模型的正视图，图3中深色颗粒即是与节理平面相接触的颗粒，这些颗粒的细观参数如表4所示，2条节理之间的连线即是岩桥。

表4 节理颗粒细观参数

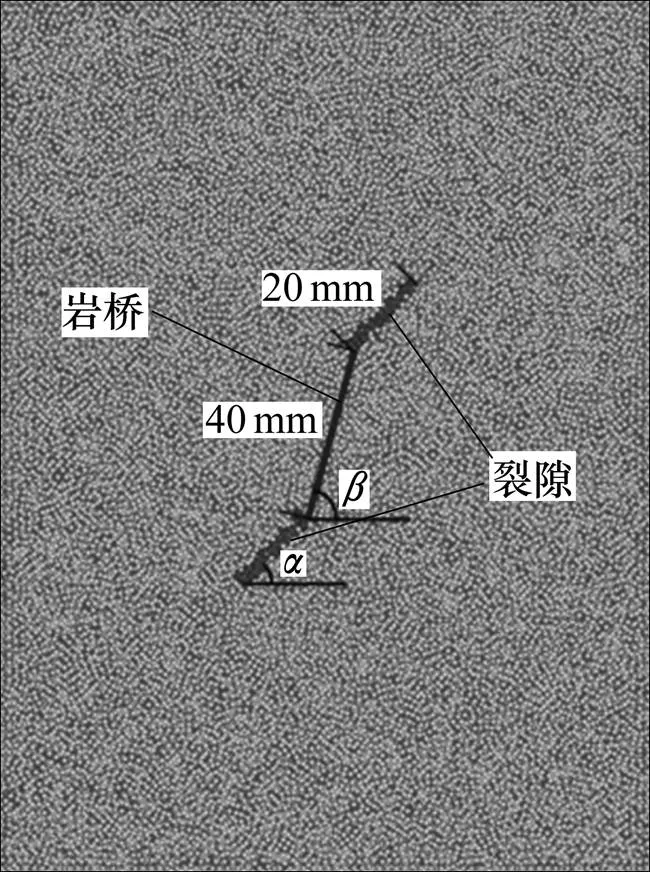
图3 裂隙布置示意图

2 数值模拟结果分析

2.1 裂隙试样强度与完整试样强度比较

为了清晰判断裂隙岩体强度、变形与完整试样的区别，同时，为了便于对比，将完整试样和裂隙试样的峰值强度与弹性模量进行了归一化处理。图4中，E和E分别为完整试样和裂隙试样的弹性模量，σ和σ分别为完整试样和裂隙试样的峰值强度。由图4可知：相对于完整试样的弹性模量，2条裂隙导致试样的弹性模量下降很小，E的下降量占完整试样弹性模量的5%左右，而且随着岩桥倾角的增加，裂隙试样弹性模量变化很小。事实上，裂隙对弹性模量有一定影响，裂隙越多，导致试样更易压缩，更加容易产生形变。本文中因裂隙数量较少，因此，弹性模量下降较小。当裂隙试样中裂隙倾角保持不变时，岩桥倾角的改变导致各裂隙试样峰值强度相对于完整试样峰值强度的下降并不大，强度下降10%~20%，当=90°时，下降量最小；当=60°时，下降量最大，这也间接说明岩桥倾角为60°对裂隙试样强度的影响最大。造成此种情况的原因是单轴荷载下岩桥贯通方式不同。

1—Ej/Ei; 2—σj/σi

2.2 岩桥倾角对裂隙试样强度、变形的影响

起裂应力是试样在承受单轴荷载时，裂纹开始产生时的轴向应力。图5所示为裂隙试样单轴抗压强度和起裂应力随岩桥倾角变化的趋势。从图5可见：当岩桥倾角在15°~90°范围内变化时，峰值抗压强度先降低后增加，当岩桥倾角为60°时，裂隙试样的峰值抗压强度最低，当岩桥倾角为90°时，峰值抗压强度最高。因为当倾角为60°时，2条裂隙非常容易沿岩桥贯通而破坏，当岩桥倾角为90°时，岩桥处最难形成贯通裂纹。由图5还可知：起裂应力与单轴抗压强度随岩桥倾角变化有近似相同的变化趋势，当=60°时，起裂应力最低，但当=15°时，起裂应力最高，而且比=90°裂隙试样的起裂应力要高。这是因为岩桥倾角不同，导致单轴荷载下裂隙试样裂隙尖端的应力分布和大小不同，导致颗粒接触黏结破坏时的轴向应力不同。因此，岩桥倾角会影响裂隙试样的峰值抗压强度和起裂应力。

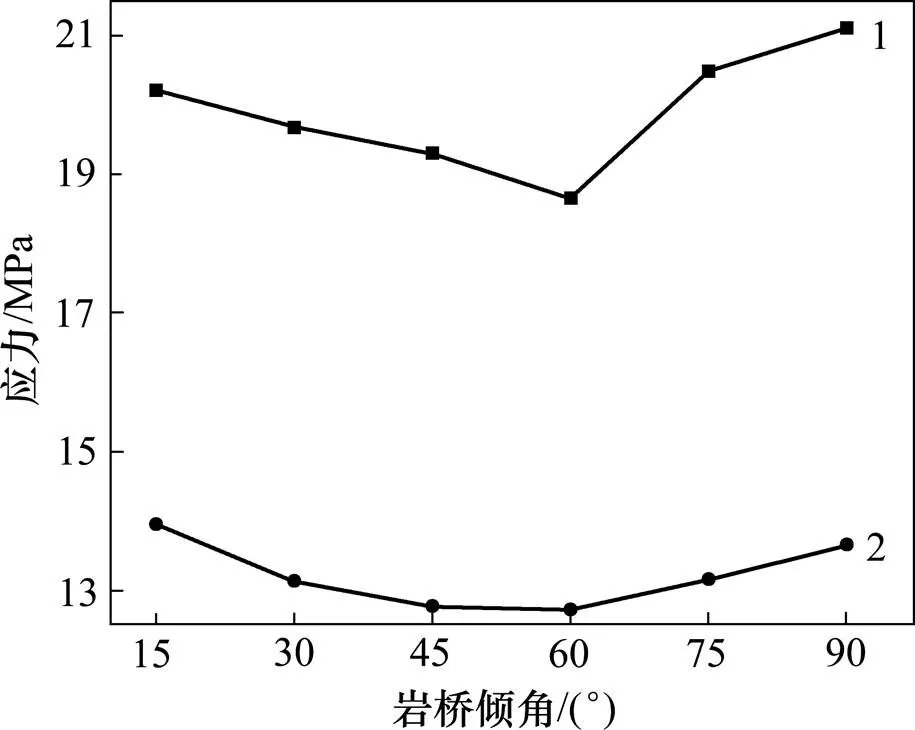
1—单轴抗压强度；2—起裂应力

已有的研究成果发现：岩体受单轴荷载时的起裂应力与其峰值强度存在一定的比例关系，但是该比值没有确定，有的学者认为该比值为0.3~0.5[16−17]，有的认为该比值为0.7~0.8[18]。采用不同方法，不同学者发现的比值有较大差别。事实上，该比值与试样中裂隙的布置有很大关系，裂隙条数、倾角和长度都会影响该比值。本文中，通过数值模拟试验得出的比值如图6所示，文中的裂隙模型只含有2条裂隙，且是闭合裂隙，在荷载作用下，裂纹表面具有一定的摩擦力。从图6可知：裂纹起裂应力与其峰值强度的比值为0.6~0.7，在裂隙倾角保持45°不变的情况下，尽管岩桥倾角从15°~90°变化，该比值变化较小，也间接说明岩桥倾角对该值没有明显影响。从图5可知：起裂应力与峰值强度随岩桥倾角有相似的变化规律，所以该比值随岩桥倾角变化较小。

图6 不同岩桥倾角裂隙试样起裂应力与峰值强度比

图7所示为裂隙试样的变形参数弹性模量、泊松比随岩桥倾角的变化趋势。对比图7和图5可知：岩桥倾角对试样峰值强度有明显的影响。但从图7发现：随岩桥倾角的增加，裂隙岩体的弹性模量变化非常小，基本上稳定在2.2 GPa附近，这说明2条裂隙间岩桥倾角对裂隙试样弹性模量几乎没有影响。泊松比是试样横向应变与纵向应变比值的绝对值。随岩桥倾角增加，裂隙试样泊松比却发生了与峰值强度不一样的变化，泊松比随岩桥倾角增加而有所降低。

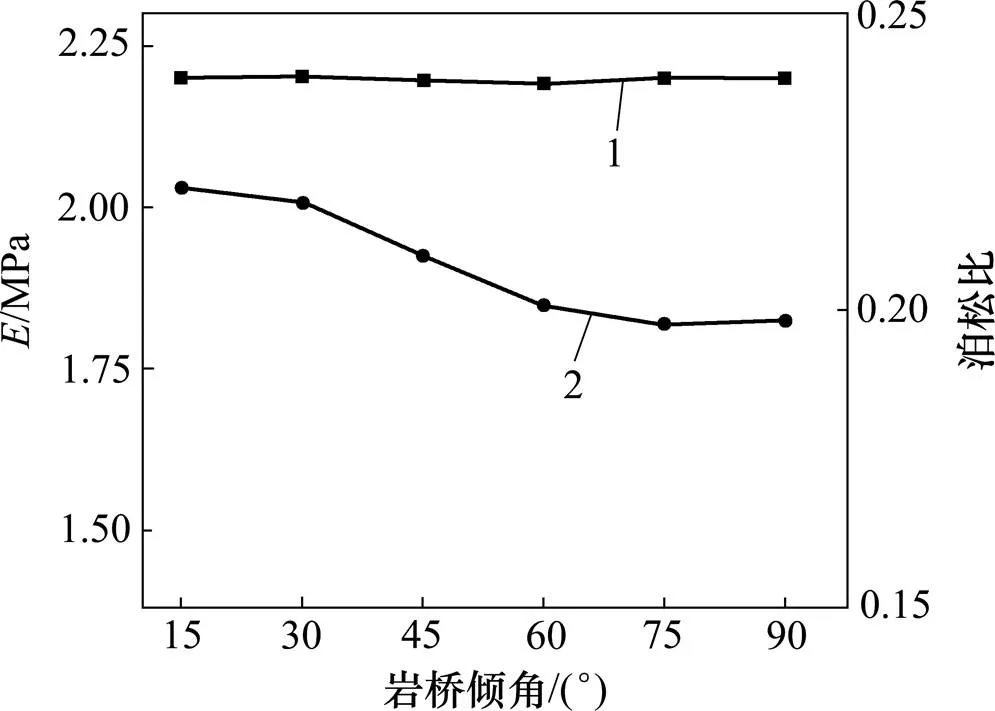
1—弹性模量；2—泊松比

2.3 应力−应变曲线分析

在本次数值模拟计算中，当实时应力为峰值应力的80%时，即停止计算。因而，得出的不同岩桥倾角试样的应力−应变曲线如图8所示，在相同的加载速率条件下，不同岩桥倾角试样达到峰值强度时的应变不同。对比图8与图5发现：随岩桥倾角的变化，峰值时刻应变的变化规律与峰值应力变化有相似之处。当岩桥倾角为60°时，裂隙试样的应变最小；当岩桥倾角为90°时，裂隙试样应变最大。除岩桥倾角为75°试样的峰值应力高于岩桥倾角为15°试样的峰值应力，但其峰值应力时的应变却小于15°试样峰值应力时的应变。而且，当采用数值模拟试验时，各试样在达到峰值强度前，有着近似线性的应力−应变关系。这与通常室内试验得到的裂隙试样应力−应变曲线不同，主要是因为室内试验存在着较多的影响因素，如端部效应、裂纹不均匀扩展、裂隙表面有效摩擦力、试样制作材料不均一性等。

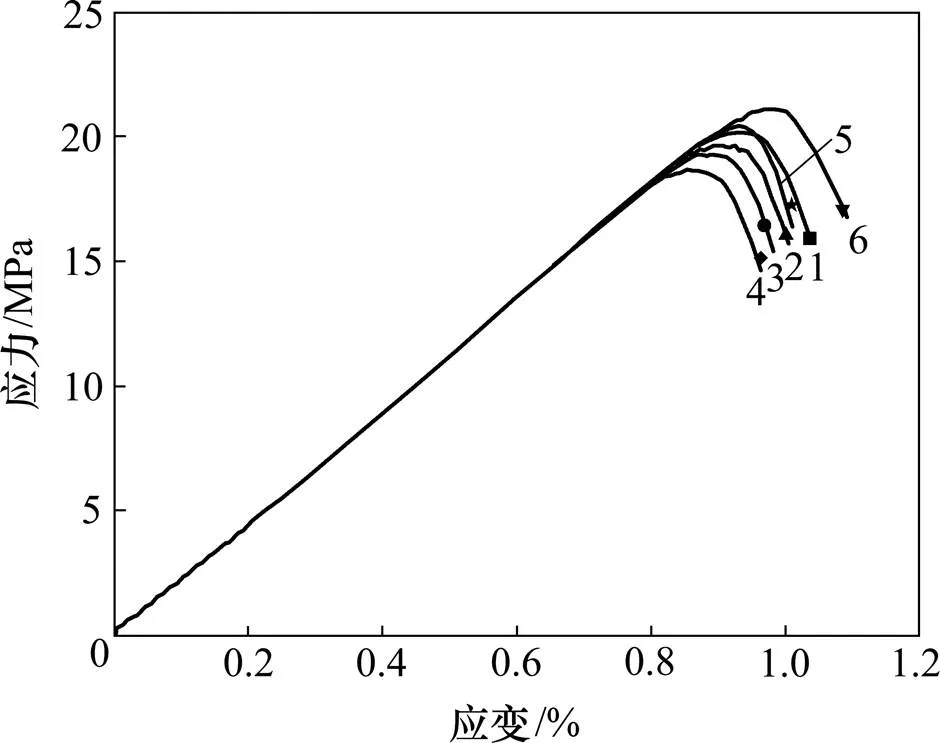
倾角/(°)：1—15；2—30；3—45；4—60；5—75；6—90

3 裂隙试样破坏方式分析

3.1 15°岩桥倾角试样

由前面分析可知：颗粒之间是通过接触黏结形成完整试样，接触黏结具有一定的强度，该强度表现为切向黏结强度和法向黏结强度。当破坏力超过其中任一强度时，该接触黏结就会被破坏。当接触黏结在切向方向发生剪切破坏时，或在法向方向发生拉伸破坏时，在黏结破坏处标记，见图9(b)。标记密集处，说明此处应力较大，容易形成破坏裂纹。

图9所示为15°岩桥裂隙试样在单轴荷载下的破坏过程。图9(a)所示为其应力−应变曲线，并在曲线上分别标记出了裂纹起裂、轴向应力为峰值应力90%、峰值应力和残余应力为峰值应力80%时的应力点，图9(b)所示为相对应轴向应力时的裂纹扩展图。首先，裂纹形成发生在裂隙的两端，这验证了裂隙尖端会形成应力集中效应。当第1条裂纹萌生时，标记出现在裂隙尖端，说明此处处于拉应力状态，会形成拉伸裂纹(见图9(b)中Ⅰ)，但此时裂纹尚未扩展，随着加载继续，裂纹与裂隙呈一定倾角方向扩展，裂隙尖端出现明显的拉伸裂纹(见图9(b)中Ⅱ)，但在裂隙尖端也存在剪应力，此时，试样并未完全破坏，还有一定的应力储备。随后，在靠近岩桥两裂隙尖端的裂纹向裂隙倾角方向扩展，最终在拉剪复合应力作用下形成了环形裂纹(见图9(b)中Ⅲ)。因为环形裂纹的出现，贯通岩桥的裂纹就没有出现，这也就是15°岩桥试样峰值强度较高的原因。当环形裂纹贯通后，终将形成一个“核”。此情形已在试验中部分试样破坏过程得到验证，如文献[4]所说的鱼眼状核，以及文献[13]中也观察到此情形。当达到峰值应力后，如继续加载，裂隙周围材料会被压碎，形成较大的破坏裂纹(见图9(b)中Ⅳ)。

(a) 15°岩桥试样应力−应变曲线；(b) 15°岩桥试样破坏图

3.2 60°岩桥倾角试样

图10所示为60°岩桥试样应力−应变曲线和破坏示意图。对比图10(a)与10(b)可知：裂隙试样在开裂前已经产生了一定的形变，但是在裂纹萌生之前，试样内颗粒之间的接触黏结都尚未破坏。随着轴向荷载的增加，第1条裂纹产生(见图10(b)中Ⅰ)，此时的轴向应力约为峰值应力的68%，应力集中出现在裂纹尖端，只是在裂隙尖端有些接触黏结因拉伸而破坏，裂隙尖端出现了少量的拉伸裂纹。随着裂隙尖端处颗粒间的接触黏结继续失效，当轴向应力为峰值应力的90%时，远离岩桥端上面一条裂隙形成剪切裂纹，但下面一条裂隙远离岩桥端形成拉伸裂纹，岩桥两端主要为拉应力，并有贯通的趋势(见图10(b)中Ⅱ)。当达到峰值应力时，岩桥贯通，沿裂隙倾向方向，试样对角出现应力集中现象(见图10(b)中Ⅲ)。如果继续施加荷载，最终会形成沿裂隙、岩桥倾向的贯通裂纹，试样在沿裂隙方向的对角也容易出现应力集中现象，相比另外2个对角的应力稍大，但是相对于裂隙周围的应力偏小(见图10(b)中Ⅳ)。因为60°岩桥试样容易沿岩桥形成贯通裂纹而破坏，所以60°岩桥试样的峰值应力较小。岩桥为30°和45°试样的破坏方式与岩桥60°试样的破坏方式相似。

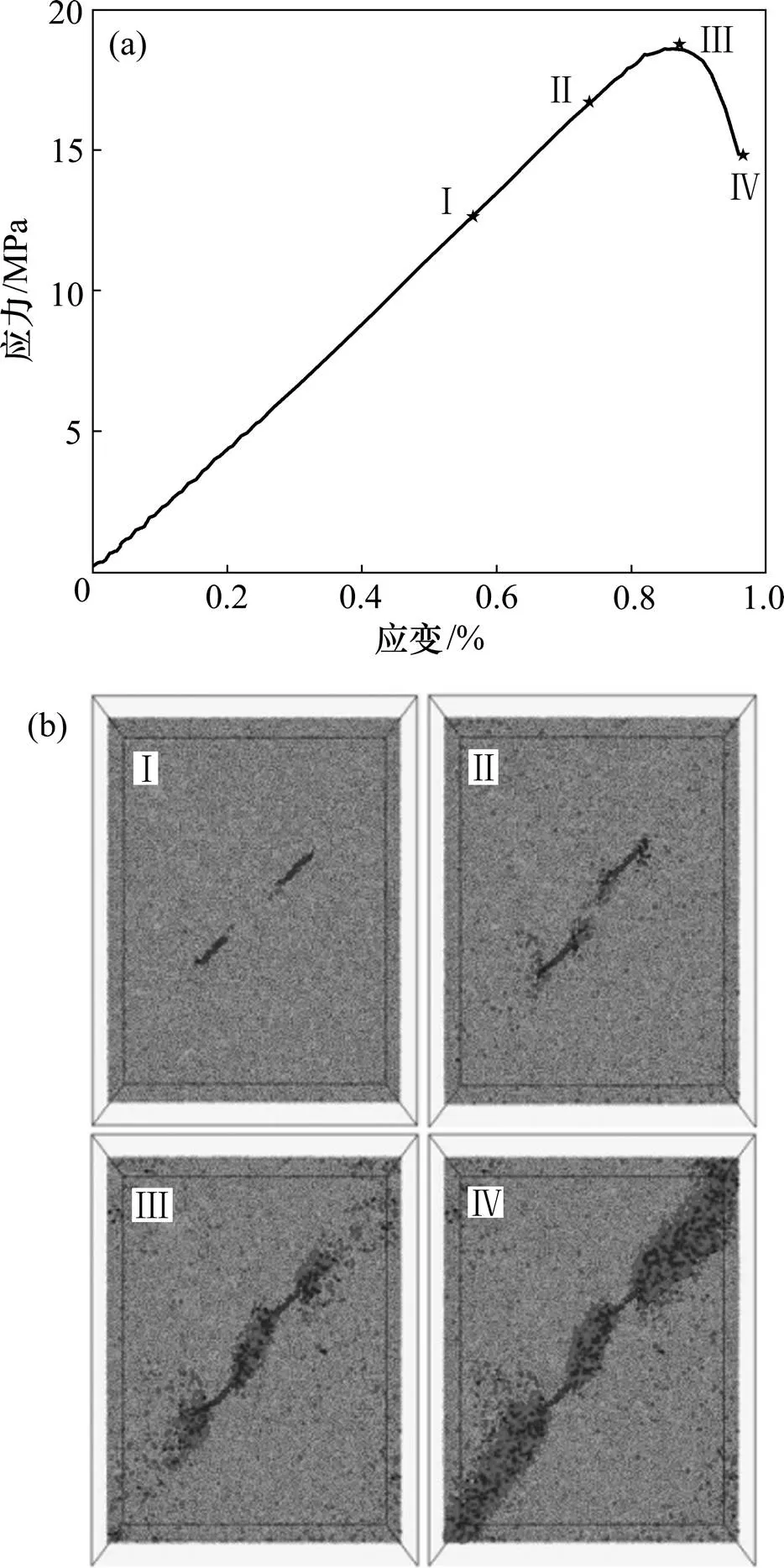
(a) 60°岩桥试样应力−应变曲线；(b) 60°岩桥试样破坏示意图

3.3 90°岩桥倾角试样

图11所示为90°岩桥试样应力−应变曲线和破坏示意图。90°岩桥试样起裂时，在裂隙尖端出现拉应力集中现象，裂纹萌生也出现在裂纹尖端(见图11(b)中Ⅰ)，当轴向应力达到峰值强度的90%时，裂纹扩展非常明显，且与裂隙呈一定倾角扩展，主要是在远离岩桥的裂隙尖端扩展，且裂纹中既有拉应力形成的裂纹，也有剪应力形成的裂纹(见图11(b)中Ⅱ)。当轴向应力达到峰值应力时，在2条裂隙远离岩桥端，分别形成了远离岩桥的翼型裂纹，翼型裂纹由拉剪复合应力形成，且裂纹有向试样纵向边界和裂隙倾角方向扩展的趋势，但是此时岩桥并未贯通，只是在岩桥两端形成了拉剪复合应力状态(见图11(b)中Ⅲ)。当裂隙试样残余强度达到峰值强度的80%时，破坏裂纹非常明显，翼型裂纹已向边界贯通，但此时岩桥仍并未完全贯通(见图11(b)中Ⅳ)。因此，90°岩桥倾角试样具有较高的峰值应力。75°岩桥试样与90°岩桥试样有近似相同的破坏模式。

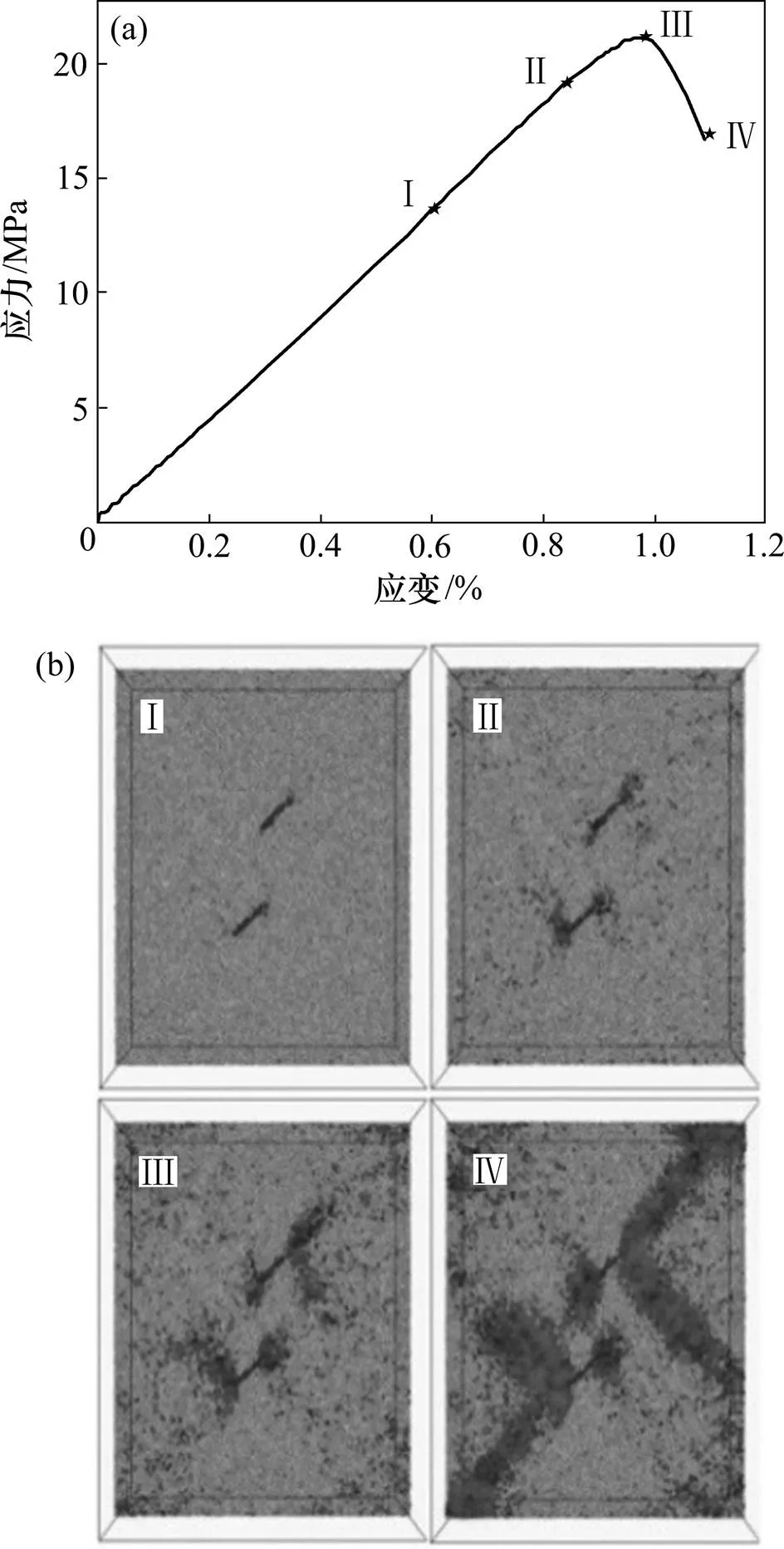
(a) 90°岩桥试样应力−应变曲线；(b) 90°岩桥试样破坏示意图

4 结论

1)岩桥倾角对含2条裂隙试样弹性模量的变化极小，但是对峰值强度和起裂应力具有较大影响。随岩桥倾角变化，裂隙试样单轴抗压强度与起裂应力有相似的变化关系。

2) 岩桥倾角影响裂隙试样在峰值应力时的应变率，除岩桥倾角75°试样外，峰值应力越大，达到峰值应力时的应变率越大。

3) 岩桥倾角影响裂隙试样的破坏模式，单轴荷载下，15°倾角岩桥试样两端形成环形裂纹，90°倾角岩桥较难贯通，60°倾角岩桥最容易形成贯通裂纹。因此，15°和90°倾角岩桥试样峰值强度比其他试样的高，60°倾角岩桥试样峰值强度最低。

参考文献：

[1] 陈新, 王仕志, 李磊. 节理岩体模型单轴压缩破坏规律研究[J]. 岩石力学与工程学报, 2012, 31(5): 898−907. CHEN Xin, WANG Shizhi, LI Lei. Characteristics of fragments of jointed rock mass model under uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(5): 898−907.

[2] 陈新, 廖志红, 李德建. 节理倾角及连通率对岩体强度、变形影响的单轴压缩试验研究[J]. 岩石力学与工程学报, 2011, 30(4): 781−789. CHEN Xin, LIAO Zhihong, LI Dejian. Experimental study of effects of joint inclination angle and connectivity rate on strength and deformation properties of rock masses under uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(4): 781−789.

[3] 黎立云, 车发星, 卢晋福, 等. 单压下类岩材料有序多裂纹体的宏观力学性能[J]. 北京科技大学学报, 2001, 23(3): 199−203. LI Liyun, CHE Faxing, LU Jinfu, et al. Macro-mechanical properties of regular cracks body in rock-like materials under uniaxial compression[J]. Journal of University Science and Technology Beijing, 2001, 23(3): 199−203.

[4] 蒲成志, 曹平, 衣永亮. 单轴压缩下预制2条贯通裂隙类岩材料断裂行为[J]. 中南大学学报(自然科学版), 2012, 43(7): 2708−2716. PU Chengzhi, CAO Ping, YI Yongliang. Fracture for rock-like materials with two transfixion fissures under uniaxial compression[J]. Journal of Central South University (Science and Technology), 2012, 43(7): 2708−2716.

[5] 蒲成志, 曹平, 赵延林, 等. 单轴压缩下多裂隙类岩石材料强度试验与数值分析[J]. 岩土力学, 2010, 31(11): 3661−3666. PU Chengzhi, CAO Ping, ZHAO Yanlin, et al. The numerical analysis and strength experiment of rock-like material with multi-fissures under uniaxial compression[J]. Rock and Soil Mechanics, 2010, 31(11): 3661−3666.

[6] Lee H, Jeon S. An experimental and numerical study of fracture coalescence in pre-cracked specimens under uniaxial compression[J]. International Journal of Solids and Structures, 2011, 48(6): 979−999.

[7] Kulatilake P H S W, Malama B, Wang J. Physical and particle flow modeling of jointed rock behavior under uniaxial loading[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(5): 641−657.

[8] 曹平, 蒲成志. 单压下有序多裂隙脆性材料破坏机制及其简化模型[J]. 中国有色金属学报, 2011, 21(10): 2659−2668. CAO Ping, PU Chengzhi. Failure mechanism and its simplified models of brittle material with ordered multi-fissures under uniaxial compression[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(10): 2659−2668.

[9] 唐春安, 刘红元, 秦四清, 等. 非均质性对岩石介质中裂纹扩展模式的影响[J]. 地球物理学报, 2000, 43(1): 116−121. TANG Chunan, LIU Hongyuan, QIN Siqing, et al. Influence of heterogeneity on crack propagation modes in brittle rock [J]. Chinese Journal of Geophysics, 2000, 43(1): 116−121.

[10] 黄明利, 唐春安, 朱万成. 非均质岩桥对裂纹扩展贯通机制影响的数值分析[J]. 辽宁工程技术大学学报(自然科学版), 2000, 19(1): 20−24. HUANG Mingli, TANG Chunan, ZHU Wancheng. Numerical simulation of the influence of heterogeneous rock bridge on the propagation and coalescence mechanism of cracks[J]. Journal of Liaoning Technical University (Natural Science), 2000, 19(1): 20−24.

[11] Tang C A, Kou S Q. Crack propagation and coalescence in brittle materials under compression[J]. Engineering Facture Mechanics, 1998, 61(3): 311−324.

[12] Wong R H C, Chau K T. Crack coalescence in a rock-like material containing two cracks[J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 35(2): 147−164.

[13] Wong L N Y, Einstein H H. Crack coalescence in molded gypsum and Carrara marble: Part 1. Macroscopic observations and interpretation[J]. Rock Mechanics and Rock Engineering, 2009, 42(3): 475−511.

[14] FAN Xiang, Kulatilake P H S W, CHEN Xin. Mechanical behavior of rock-like jointed blocks with multi-non-persistent joints under uniaxial loading: A particle mechanics approach[J]. Engineering Geology, 2015, 190(5): 17−32.

[15] Itasca Consulting Group. PFC3Duser’s manual, version 4.0[M]. Minneapolis, USA: Minnesota, 2003: 100−300.

[16] FAN Xiang, Kulatilake P H S W, CHEN Xin, et al. Crack initiation stress and strain of jointed rock containing multi-cracks under uniaxial compressive loading: A particle flow code approach[J]. Journal of Central South University, 2015, 22(2): 638−645.

[17] Holcomb D J, Costin L S. Damage in brittle materials: Experimental methods[R]. Albuquerque, NM, USA: Geomechanics Division, Sandia National Labs, 1986: 1−50.

[18] Martin C D, Chandler N A. The progressive fracture of Lac du Bonnet granite[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1994, 31(6): 643−659.

Numerical analysis of mechanical behavior of rock sample with two flaws under uniaxial compressive loading based on PFC3D

FAN Xiang1, 2, CAO Ping1

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;2. School of Highway, Chang’an University, Xi’an 710064, China)

Based on the contact-bonded model in Particle Flow Code 3D, a discrete element method software, a numerical model with two flaws was established and the micro-parameters for this model were obtained by calibrating experimental data. The slant angle of rock bridge was set to the degrees from 15° to 90° with an interval of 15°. The effect of rock bridge angle on peak strength, crack initiation stress, elastic modulus, failure mode and strain at the point of peak stress was investigated. The results show that for the numerical rock sample with two flaws, the slant angle of rock bridge has little influence on elastic modulus, but major influence on peak strength and crack initiation stress. As slant angle of rock bridge changes, the changing relation between uniaxial compressive strength and rock bridge angle is similar to that between crack initiation stress and rock bridge angle. Rock bridge angle has some effect on the strain at the point of peak strength and crack propagation, and it is easy to coalesce for 60° rock bridge but hard for 15° and 90° rock bridge.

numerical simulation; PFC3D; flaw; rock bridge; crack propagation

10.11817/j.issn.1672-7207.2015.07.034

TU52

A

1672−7207(2015)07−2635−08

2014−07−04；

2014−10−02

国家自然科学基金资助项目(51174228)；国家留学基金委资助项目(201206370124) (Project(51174228) supported by the National Natural Science Foundation of China; Project(201206370124) supported by the China Scholarship Council, China)

曹平，教授，博士生导师，从事岩石断裂力学研究；E-mail: pcao_csu@163.com

(编辑 杨幼平)