水中悬浮隧道锚索参数振动分析和控制

李 颂，林 钢，巫志文

(中山大学 工学院，广东 广州 510006)

水中悬浮隧道锚索参数振动分析和控制

李 颂，林 钢，巫志文

(中山大学 工学院，广东 广州 510006)

为了进一步研究水中悬浮隧道锚索的参数振动以及振动控制，考虑到流的影响，建立水中悬浮隧道锚索的非线性振动模型，并利用数值方法推导求解了锚索的非线性振动方程，同时采用一种被动质量阻尼器进行振动控制。研究结果表明：锚索的参数振动与锚索的初张力、参数激励幅值、频率比有关，并具有明显的非线性特征；流的作用会对锚索的参数振动幅值产生一定影响，但流的作用不会改变锚索的共振规律；对锚索参数振动提出的振动控制装置，计算结果表明具有良好的减振效果。

水中悬浮隧道；锚索；参数振动；流的作用；振动控制

图1 锚索式悬浮隧道Fig. 1 Submerged floating tunnel supported by anchors

水中悬浮隧道SFT(submerged floating tunnel),又称阿基米德桥(Aechimede’s bridge)，是一种悬浮在适当水深位置的管状通道[1]，作为继海底隧道和大跨度桥梁后跨越水域的又一种选择，主要用于跨越海峡、海湾、湖泊等受环境限制的水域，适用于所有需要在水中穿行的交通运载工具，可通行火车、汽车、小型机动车和行人，还可做穿行各种管道和电缆的服务隧道[2]。锚索式悬浮隧道基本结构包括四个部分[3]：悬浮在水面以下一定深度的管状结构；锚固在水下基础的锚索装置；桥体管节之间的连接装置；隧道与两岸相连的构筑物。锚索式悬浮隧道的结构示意，如图1所示。

锚索作为平衡悬浮隧道管体剩余浮力的关键结构，是确保悬浮隧道竖向稳定性的重要构件[4]。水中悬浮隧道锚索阻尼小，质量轻，柔度大，在水下复杂的波流环境中，是一种极易发生振动的构件[5]。因此，研究水中悬浮隧道锚索的振动问题极为重要[6]，很多专家学者已经对此做了大量的工作。陈健云等[7]全面地进行了锚索在流作用下的动力分析；葛菲等[8]对锚索非线性涡激振动进行了深入研究；董满生等[9]研究了锚索在随机地震激励作用下的动力响应；孙胜男等[10]系统分析了锚索在轴向激励下的参数振动。但是目前的研究，未考虑初张力的改变、以及流的作用对锚索参数振动的影响，并且关于水中悬浮隧道锚索振动控制的研究非常少，当前大部分的研究工作几乎没有涉及锚索振动控制方面。本文在陈健云和孙胜男的研究成果基础上进一步探究水中悬浮隧道锚索参数振动问题：①考虑在不同初张力情况下，激励幅值与锚索参数振动最大振幅的关系，以及频率比与锚索参数振动最大振幅的关系。②对比分析在有流作用和无流作用时，激励幅值、频率比与锚索参数振动最大振幅的关系。③从锚索参数振动原理出发，首次提出被动质量阻尼器的减振方法，针对该方法进行计算，根据计算结果分析振动控制的效果。

1 锚索非线性振动模型

为方便研究并简化问题，同时又能体现问题的本质。参考陈健云[7]和孙胜男[10]建立的模型，对锚索式悬浮隧道进行简化，建立锚索的非线性参数振动模型，如图2所示。

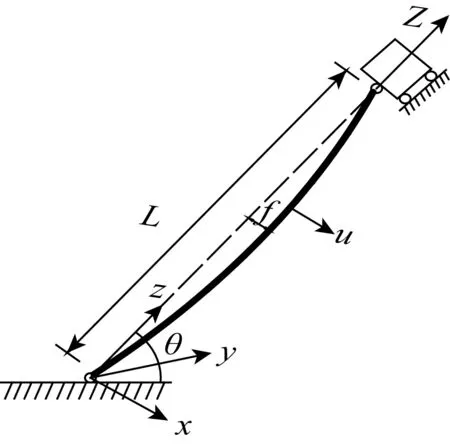
图2 锚索非线性振动模型Fig. 2 Non-linear vibration model of tether

本文的基本假定：

1) 锚索的初张力、几何尺寸、刚度和材料性质沿长度方向不变。

2) 锚索的抗弯刚度很小，可以忽略不计。

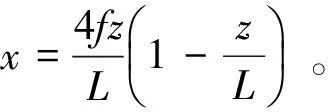
4) 悬浮隧道管体对锚索顶端张力变化产生的参数激励，与车辆通过时引起悬浮隧道的响应频率相同。根据高等结构动力学[16]，锚索受到隧道简谐振动激励的作用，将其简化为作用在锚索端部的轴向激励，并选取激励方程为：z=zcsinωct，其中zc为参数激励的幅值，ωc为参数激励的频率。

5) 忽略锚索与流体的动力耦合作用，并只考虑单根锚索的情况，不考虑锚索之间的相互影响。

在上述假定条件下，对锚索顶端施加动荷载后，锚索的动力构型用位移u来表示，u为沿与锚索轴向的法线方向由静力平衡位置开始的位移。根据Hamilton原理，可以得到锚索的振动方程为[11]：

考虑到降低计算难度的要求，根据线性化的Morison公式[12-13]，锚索横向振动引起的水体对其的单位长度上的总作用力：

悬浮隧道锚索的垂跨比很小(f/L<1/8),取锚索的振动模态为标准弦的振动模态[14]，采用分离变量法将锚索的振动模态表示为：

Tagata[15]由试验指出，张紧弦在端部激励作用下的振动，其中占主要地位的是基本模态，所以采用伽辽金(Galerkin)法[16]取一阶振动模态化简式(1)，最终整理得：

同理,受到流的作用时锚索振动方程[7]：

式中:CL为脉动横向力系数，取CL=0.7；ωv为尾流漩涡泄放频率，取ωv=ωf。

2 数值算例

基本参数选取参考国外拟建悬浮隧道的设计参数：总水深为170 m，隧道放置在水下30 m处，其它具体参数的取值，如表1所示。在MATLAB中编程计算，利用四阶的龙格—库塔法[17]进行数值求解。

2.1参数振动的激励幅值分析

当参数激励频率与锚索固有频率的比值ωc/ωf=2时，分别取锚索初张力为T0=8.572×106N、T0=2.572×107N、T0=4.572×107N，得到锚索最大振幅与激励幅值的关系，如图3所示。分析比较这三条曲线可以看出，锚索最大振幅随着激励幅值的增大而增大。锚索受到的初张力增大，锚索最大振幅会随着减小。

当参数激励频率与锚索固有频率的比值ωc/ωf=2时，取锚索初张力为设计值T0=2.572×107N，有流作用时取尾流漩涡泄放频率ωv=ωf，得到锚索在有流作用和无流作用时锚索最大振幅与激励幅值的关系，如图3所示。从图中可以看出，流的作用增大了锚索最大振幅，特别是当参数振动的激励幅值小于0.04 m时这一作用很明显。但如果一直保持尾流漩涡泄放频率ωv=ωf不变，随着激励幅值继续增大，尤其是激励幅值大于0.08 m时，流的作用对于锚索最大振幅的继续增大几乎没有影响，说明此时随着激励幅值的增大，流的作用对锚索振动的影响会相对减弱。

2.2参数振动的激励频率分析

当取锚索参数振动的激励幅值为0.1 m时，分别取锚索初张力为T0=8.572×106N，T0=2.572×107N，T0=4.572×107N，得到锚索最大振幅与频率比的关系，如图4所示。从图中可以看出，因为锚索受到的初张力会改变锚索的振动频率，但初张力无法改变激励频率，所以锚索受到的初张力对锚索共振规律的影响很小。锚索产生共振所对应的频率比以及锚索最大振幅，受初张力变化的影响很小。

当取锚索参数振动的激励幅值为0.1 m时，不断改变锚索参数振动的激励频率ωc与锚索固有频率ωf的比值，得到锚索最大振幅与频率比ωc/ωf的关系，如图4所示。据图可知，锚索最大振幅有三个峰值，同时也可看出峰值并不正好在ωc/ωf为0.5、1、2处，而是在它们的右边，这反映出锚索参数振动的非线性特征。保持尾流漩涡泄放频率ωV=ωf，流的作用对锚索共振规律的影响也很小，锚索产生共振所对应的频率比基本上不改变，产生共振时的锚索最大振幅基本上也不改变；但在非共振区域，流的作用会使锚索最大振幅有所增加。

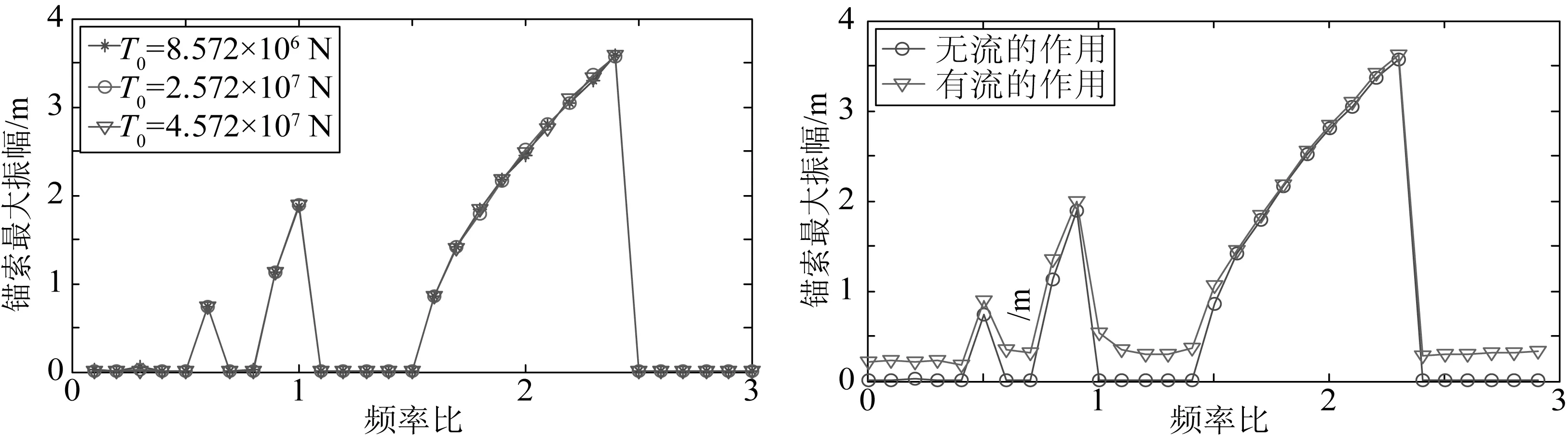
图4 频率比与锚索最大振幅的关系Fig. 4 Relation between maximum amplitude of tether and frequency ratio

2.3参数振动的控制

水中悬浮隧道锚索参数振动从原理上看，是因为锚索受到隧道简谐振动激励的作用。从这一角度出发，采用一种被动的质量阻尼器进行锚索的参数振动控制[18]，如图5所示。

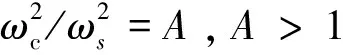
因为阻尼器位于锚索的端部，所以锚索振动对阻尼器基本上没有影响，阻尼器的振动取决于隧道管体的振动。由于阻尼器的振动与隧道管体的振动完全反向，阻尼器将对锚索产生于隧道完全相反的激励，从而抑制锚索的参数振动。阻尼器的作用反映到锚索振动方程中，要将T0改为T0-Tssinωct(其中Ts为阻尼器产生的阻尼激振力)。

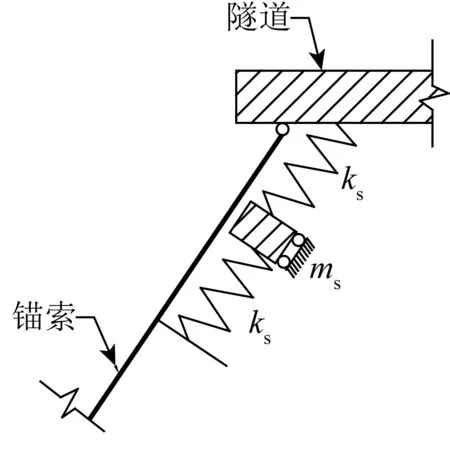
图5 锚索参数振动控制装置Fig. 5 Control device for parametric vibration of tether

根据前面得到的研究结论，取ωc/ωf=2.4，T0=2.572×107N，锚索参数振动的激励幅值为0.1 m，并考虑流的作用，得到此时锚索的位移响应曲线，如图6(a)所示。此时锚索最大振幅为3.628 m,位移均方根为2.046 9 m，位移标准差为2.048 9 m。在以上条件都不改变的情况下，进行锚索振动控制研究，对阻尼器施加大小为锚索初张力5%的阻尼激振力，得到振动控制后的锚索位移响应曲线，如图6(b)所示。此时锚索最大振幅为0.386 5 m,位移均方根为0.273 9 m，位移标准差为0.274 1 m。阻尼器作用之后，锚索最大振幅减小了近10倍，这说明阻尼器对锚索参数振动的控制是十分有效的。

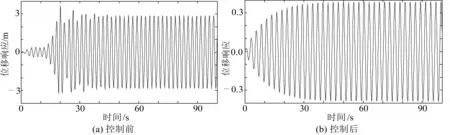
图6 锚索位移响应曲线Fig. 6 Displacement response curve of tether

3 结 语

1) 锚索最大振幅随激励幅值增大而增大，随初张力增大而减小。故，对参数激励幅值进行限制，适当增大锚索受到的初张力，将减弱锚索的振动，提高锚索的抗振能力。

2) 流的作用可使锚索产生涡激谐振，从而对锚索振动产生影响。但如果尾流漩涡泄放频率ωv=ωf保持不变，随着激励幅值的增大，流的作用对锚索振动的影响会相对逐渐减小。

3) 锚索参数振动具有非线性特征，锚索受到的初张力会改变锚索的振动频率，但初张力无法改变激励频率，所以锚索受到的初张力对锚索共振规律的影响是有限的。流的作用对锚索共振规律的影响也是有限的，但流的作用会使非共振区域的锚索最大振幅有所增加。

4) 在锚索端部安装被动质量阻尼器的减振方法，从计算结果来看，对于控制锚索的参数振动具有良好的效果。

[1] AHRENS D. Submerged floating tunnels-A concept whose time has arrived[J]. Tunneling and Underground Space Technology, 1997, 12(2):317-336.

[2] 董满生，葛斐，惠磊,等.水中悬浮隧道研究进展[J].中国公路学报，2007,20(4)：101-107. (DONG Mansheng, GE Fei, HUI Lei, et al. Research progress in submerged floating tunnels[J]. China Journal of Highway and Transport, 2007,20(4)：101-107. (in Chinese))

[3] BRANCALEONI, CASTELLANI A, D’ASDIA P. The response of submerged tunnels to their environment[J]. Engineering Structures, 1989, 11(1):47-56.

[4] 李剑.水中悬浮隧道概念设计及其关键技术研究[D].上海：同济大学，2003. (LI Jian. Connectional design and key problems for submerged floating tunnel[D]. Shanghai: Tongji University, 2003. (in Chinese))

[5] DI PILATO M, PEROTTI F, FOGAZZI P. 3D dynamic response of submerged floating tunnels under seismic and hydrodynamic excitation[J]. Engineering Structures, 2008, 30(1):268-281.

[6] 陈健云，孙胜男.水下悬浮隧道结构分析研究进展[J].海洋工程，2008,26(3)：111-118. (CHEN Jianyun, SUN Shengnan. Progress of structural studies of submerged floating tunnel[J]. The Ocean Engineering, 2008,26(3)：111-118. (in Chinese))

[7] 陈健云，孙胜男，王变革.水下悬浮隧道锚索的动力分析[J].计算力学学报，2008,25(4)：488-493. (CHEN Jianyun, SUN Shengnan, WANG Biange . Dynamic analysis for the tether of submerged floating tunnel[J]. Chinese Journal of Computational Mechanics, 2008,25(4)：488-493. (in Chinese))

[8] 葛斐，董满生，惠磊.水中悬浮隧道锚索在波流场中的涡激动力响应[J].工程力学，2006,23(S1)：217-221. (GE Fei, DONG Mansheng, HUI Lei . Vortex-induced vibration of submerged floating tunnel tethers under wave and current effects[J]. Engineering Mechanics, 2006, 23(S1)：217-221. (in Chinese))

[9] 董满生，赵佳佳，牛忠荣,等.随机地震激励作用下水中悬浮隧道锚索的动力响应[J].合肥工业大学学报:自然科学版，2013,36(1)：74-78.(DONG Mansheng, ZHAO Jiajia, NIU Zhongrong, et al . Dynamic response of submerged floating tunnel’s anchor cable to random seismic excitation[J]. Journal of Hefei University of Technology, 2013, 36(1):74-78. (in Chinese))

[10] 孙胜男，苏志彬，白卫峰.轴向激励下悬浮隧道锚索参数振动分析[J].工程力学，2011,28(6)：170-175. (SUN Shengnan, SU Zhibin, BAI Weifeng . Parametric vibration analysis of submerged floating tunnel tether caused by axial excitation[J]. Engineering Mechanics,2011,28(6)：170-175. (in Chinese))

[11] SUN Shengnan ,CHEN Jianyun, LI Jing. Non-linear response of tethers subjected to parametric excitation in submerged floating tunnels[J]. China Ocean Engineering, 2009, 23(1):167-174.

[12] 竺艳蓉. 海洋工程波浪力学[M]. 天津：天津大学出版社，1991.(ZHU Yanrong. Ocean engineering wave mechanics[M]. Tianjin: Tianjin University Press, 1991. (in Chinese))

[13] 马海龙.基于黏弹性阻尼器的海洋平台振动控制[D].青岛：中国海洋大学，2003：18-20. (MA Hailong . Vibration control of offshore platform with viscoelastic dampers[D]. Qingdao: Ocean University of China, 2003:18-20. (in Chinese))

[14] IRVINE H M. Cable structures[M]. Cambridge: Massachusetts Institute of Technology Press, 1981:98-132.

[15] TAGATA G. Harmonically forced, finite amplitude vibration of a string[J].Journal of Sound and Vibration, 1977, 51(4):438-492.

[16] 唐友刚.高等结构动力学[M].天津：天津大学出版社，2002:222-228. (TANG Yougang. Advanced structural dynamics[M]. Tianjin: Tianjin University Press, 2002:222-228. (in Chinese))

[17] JOHN H, MATHEWS, KURTIS D F. Numerical methods using MATLAB[M]. Beijing：Publishing House of Electronics Industry, 2005 .

[18] PERKINS N C. Modal interactions in the non-linear response of elastic cables under parametric/external excitation[J]. International Journal of Non-Linear Mechanics, 1992, 27(2):233-250.

Parametric vibration analysis and control of submerged floating tunnel tethers

LI Song， LIN Gang， WU Zhiwen

(School of Engineering, Sun Yat-Sen University, Guangzhou 510006, China)

To further study the parametric vibration of a submerged floating tunnel tether and vibration control of tether, a nonlinear vibration model of submerged floating tunnel tether is proposed considering the influence of the flow. The non-linear vibration equation of a submerged floating tunnel tether is derived, and solved by numerical method. Adopting a passive mass damper, we control the vibration of tether. It may be concluded that the parametric vibration response of a submerged floating tunnel tether is related to tension excitation and frequency ratio damping, and the parametric vibration response of a submerged floating tunnel tether has obvious nonlinear characteristics. The parametric vibration amplitude of tether can be affected by flow, but the flow can’t affect the resonance law of tether. Numerical results show that the vibration control device of tether is considerably effective.

submerged floating tunnel(SFT); tether; flow; parametric vibration; vibration control

U459.5

A

10.16483/j.issn.1005-9865.2015.06.015

1005-9865(2015)06-106-06

2014-09-23

李 颂(1990-)，男，云南大理人，硕士生，主要从事悬浮隧道锚索动力响应研究。E-mail：lisong25@mail2.sysu.edu.cn