迷宫活塞压缩机活塞组件精确导向技术研究(一)
——活塞组件运动特性分析
2015-10-27程军明曾翔君余小玲冯全科
程军明,曾翔君,余小玲,冯全科
(西安交通大学能源与动力工程学院,陕西西安710049)
迷宫活塞压缩机活塞组件精确导向技术研究(一)
——活塞组件运动特性分析
程军明,曾翔君,余小玲,冯全科
(西安交通大学能源与动力工程学院,陕西西安710049)

在现行的迷宫活塞压缩机中,活塞往往处于偏心运行状态。在工程中,活塞与气缸之间径向单边间隙达到0.2~0.5 mm,才能避免活塞与气缸镜面的摩擦,然而,该间隙导致泄漏严重,造成压缩机效率较低,这已成为迷宫活塞压缩机向前发展的最大障碍。基于此,建立了往复式迷宫压缩机活塞组件多体动力学仿真模型,分别模拟了活塞杆为刚体和柔体时活塞在气缸中的运动特性,得出了活塞的偏心轨迹及其偏心量,为下一步研究活塞组件的精确定心技术奠定理论依据。
迷宫活塞压缩机;活塞运动;多体动力学;泄漏
1 引言
迷宫式活塞压缩机是石化行业的关键主配套设备,具有很高的制造和配合精度要求。与传统往复压缩机相比,迷宫活塞压缩机气缸与活塞、活塞杆与填料间采用非接触式迷宫密封,实现了排气无油,对压缩介质没有任何污染;对于具有易燃易爆、腐蚀性以及其他污染环境的气体时,采用封闭的机型,可以完全杜绝气体的泄漏,具有极高的安全可靠性;同时,迷宫活塞压缩机的工作温度区间更加宽阔,在苛刻的超高温或超低温工况中,迷宫活塞压缩机很可能是唯一的选择。
活塞与气缸之间保持精确定心是实现迷宫密封的先决条件之一,目前在国内外生产的迷宫活塞压缩机中,活塞的导向是依靠十字头滑道和活塞杆中部的导向轴承来实现的。
活塞相当于是外悬在活塞杆一端的受导向元件,而且活塞上时刻承受着具有周期性变化的巨大载荷,如气体力、往复惯性力等,另外受到导向轴承安装位置、活塞杆与导向轴承之间的配合间隙、十字头与滑道之间的间隙、活塞组件的振动、机壳的振动等多种因素的综合影响,导致活塞在做高速往复运动时发生径向的偏心,造成活塞与气缸壁的擦撞。在工程实际中,为避免活塞与气缸之间的擦撞,活塞与气缸壁面之间的单边间隙达到0.2~0.5 mm[1]。由于此间隙引起压缩气体的泄漏量大(泄漏量达到20%~30%)、效率低(容积效率仅为50%~60%),造成能源巨大的浪费。由此看出,多年以来迷宫式活塞压缩机效率低下,发展缓慢,其本质原因在于活塞的偏心一直未得到有效的控制和解决。
针对迷宫式活塞压缩机活塞的偏心,国内外学者做了大量的分析研究。如王玲娣[2]从理论上对活塞与活塞杆组件的振动系统进行了分析,介绍了求解振动系统的自振频率和稳定状态下活塞的振幅;董新宇[3]等对迷宫式压缩机活塞杆进行了模态分析、谐响应分析和屈曲分析,得到导向轴承安装位置对活塞杆的影响;李玉艳[4]等建立了迷宫压缩机活塞杆二维力学模型,采用有限元软件Ansys对活塞杆进行含预应力的模态分析。然而以上模型仅仅将活塞杆作为研究对象,并不能直观反映出活塞在气缸中的运动特性以及活塞的偏心量。
基于此,本文结合柔体动力学理论,应用Ansys和Adams两大分析软件,提出了一种迷宫压缩机活塞径向偏心量的计算方法,并以某公司生产的一台型号为4K-300MG的往复式迷宫压缩机为例,对活塞-活塞杆组件进行运动特性分析,为本课题组下一步研究活塞精确定心的技术提供依据。
2 活塞运动规律的理论分析
图1所示为迷宫式活塞压缩机活塞运动简图,其中M表示活塞,B为导向轴承,A为十字头,l为活塞杆长度,x表示活塞相对于导向轴承B的坐标。由于活塞是外悬在活塞杆一端的受导向部件,导致活塞偏心运行是多种因素综合作用的结果,其中最关键的因素主要是以下2个方面:(1)活塞上时刻承载具有周期性的巨大气体力以及往复惯性力,迫使活塞杆发生弯曲振动;(2)十字头处与导向轴承处存在间隙,活塞组件在运行中发生摆动。而在实际中,活塞的偏心是以上两者的耦合。
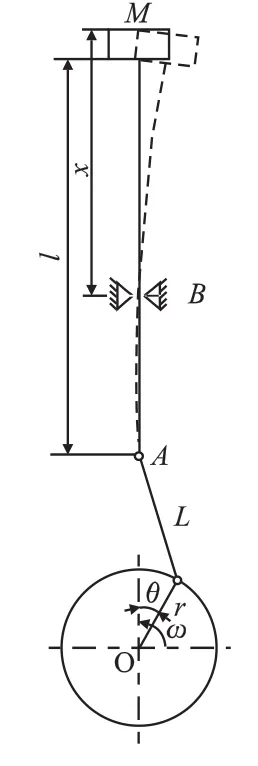
图1 往复式迷宫压缩机活塞组件运动图
2.1活塞杆为刚性的几何模型
假设当活塞杆为刚性体,即活塞杆不会发生弯曲效应,则活塞杆运动特性的几何模型如图2所示。

图2 刚性活塞杆运动的几何模型
根据几何关系可知

联立式(1)、(2)可解得活塞的偏心量为

其中δ1——活塞中心径向偏心位移
δ2——导向轴承处间隙
δ3——十字头处间隙
O′O"——气缸中心线
a——导向轴承上顶面与活塞中心之间的距离
b——导向轴承中心与活塞中心之间的距离
l——十字头中心与活塞中心之间的距离
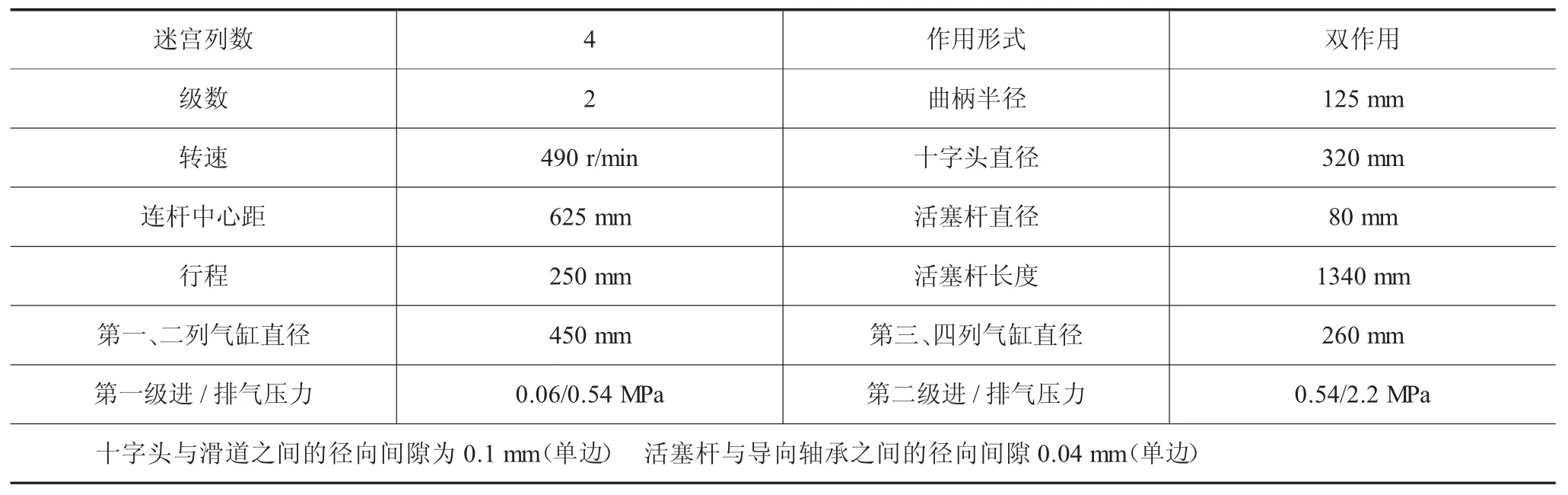
表1 往复式迷宫压缩机主要参数
其中a和b值随着活塞的运动而做周期性的变化,而l、δ2、δ3可认为是常数。
2.2活塞杆为弹性的有限元模型
目前,利用有限元离散方法进行模态分析已成为分析结构振动特性的主要手段。根据振动理论,离散后的活塞杆可看做是一个多自由度的弹性杆体,其运动状态中各节点的动力平衡方程[4]为
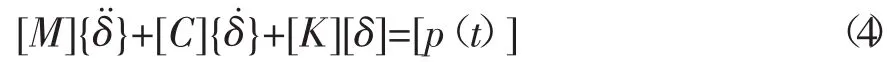
其中[M]——为质量矩阵
[C]——为阻尼矩阵
[K]——为刚度矩阵
[p(t)]——激振力矩阵
{δ}——位移向量
令系统的阻尼和外力[p(t)]等于零,则可得到活塞杆n自由度振动方程

设其主振动方程为

其中{φ}——主振型
将式(6)代入式(5),可导出活塞杆的振型方程

上式方程存在非零解{φ}的充要条件是系数行列式为零,并令,即

上式成为关于λ的特征多项式,λ称为特征值,即系统自由振动的固有频率,由式(8)可求得n个固有频率,将所得每阶固有频率代入式(7),则可得每阶固有频率所对应的主振型φi,因此振动问题被转化为求解固有频率的问题。
3 构建多体动力学仿真模型
本文以一台型号为4K-300MG的立式迷宫活塞压缩机为研究对象,其迷宫压缩机主要参数如表1所示。由于活塞在气缸中的运动状态各列之间并无影响,因此,本文以第一列为例,进行建模仿真,分别模拟了活塞杆为刚性体和柔性体时,活塞在气缸中径向偏心轨迹和偏心量。
3.1构建柔性活塞杆
首先在Ansys软件中建立活塞杆三维有限元模型,并对活塞杆实体进行网格划分,然后将活塞杆有限元模型输出到Adams中,生成模态中性文件(MNF),即为活塞杆的柔体模型,MNF文件包含了柔性体的弯曲刚度、质量、转动惯量、质心、频率、振型以及对载荷的参与因子等信息,图3所示为活塞杆柔体模型。
3.2建立仿真模型
在三维制图软件Soildworks中建立其它运动部件,通过Soildworks与Adams的接口导入Adams软件中,在各部件的连接处建立连接点(interface point),将各个部件按照实际运动状态在连接处连接起来,并在连接点处添加相应的运动副。其中活塞、十字头、曲轴、连杆、导向轴承以及十字头滑道均为刚性体,建立好的单列迷宫压缩机运动机构仿真模型如图4所示。

图3 活塞杆柔体模型

图4 多体动力学仿真模型
3.3载荷的施加与边界条件的确定
气体力属于外部载荷,要加载到模型中,往复惯性力在Adams软件的仿真过程中会实现自动计算,不需要另外加载。十字头与滑道、活塞杆与导向轴承之间均存在有径向间隙,因此其相对运动可分为“接触、分离”两种状态[5],为保证模拟精度,本文在十字头与滑道之间、活塞杆与导向轴承之间分别设置带有间隙副的接触力函数,即在构件的运动副之间添加了一个非线性弹簧阻尼来定义其相互之间的运动状态。
图5所示为第1列活塞气体力随曲轴转角变化曲线,其中轴侧与盖侧的气体力采用相同的曲轴转角基准,即活塞处于上止点时,曲轴转角∂=0°,当活塞处于下止点时,∂=180°。
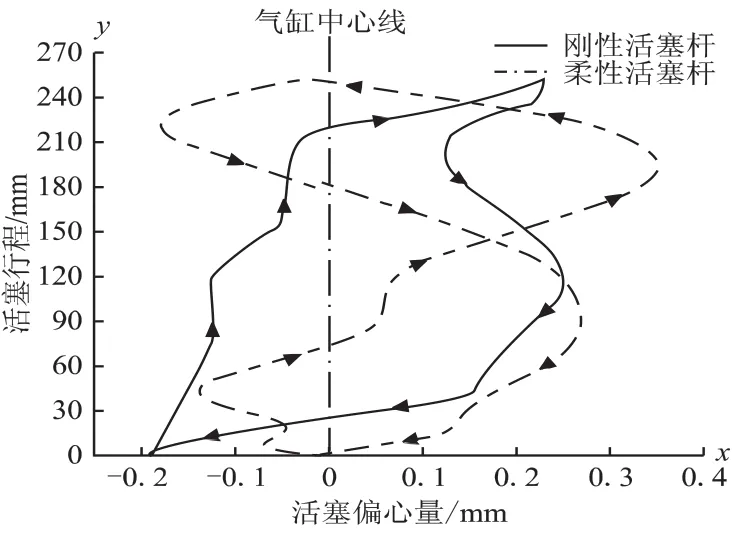
图5 第1列活塞气体力随曲轴转角变化曲线
4 结果分析
图6中实线表示活塞杆为刚性体时活塞在气缸中径向偏心轨迹,箭头指示方向为活塞在整个行程中各时刻的偏心运动方向,其中x负半轴方向与连杆平面内十字头主要承受的侧向力方向相同。由图看出,活塞杆为刚性体时,活塞径向偏心量主要在-0.17~0.23 mm之间变化,在向上行程中,活塞主要偏向x负半轴,而在向下行程时则主要偏向x正半轴。图中虚线所示活塞杆为柔性体时活塞的径向偏心轨迹,活塞在整个行程中主要偏向x的正半轴,且其偏心量主要在-0.18~0.35 mm之间变化,活塞偏心量比活塞杆为刚性体时较大。当活塞杆为柔性体时,活塞杆在气体力作用下,活塞杆会发生微小的弯曲效应,导致活塞在气缸中的偏心轨迹呈现出“8”字型,而活塞杆为刚性体时,气体力不能使得活塞杆产生弯曲效应,因此

图6 活塞偏心轨迹
活塞偏心轨迹也不能显现出“8”字型。由此可看出,当活塞杆为柔性体时,模型更具有合理性,且仿真结果更逼近活塞的实际运行状况。
5 结语
在工程实际中,迷宫式活塞压缩机中活塞的偏心多种因素的综合作用的结果,其中十字头处与导向轴承处的径向间隙,活塞杆的弯曲振动特性是造成活塞偏心最为关键的2个因素。而活塞的真实偏心量主要是以上两方面原因的耦合。因此,为进一步提高模拟精度,本文联合Ansys和Adams两大分析软件,提出了一种新的预测活塞偏心的计算方法。通过建立活塞杆的柔性体,可同时考虑活塞杆的弯曲和振动特性。而在十字头处与导向轴承处设置带有间隙副的接触力函数,定义活塞杆与导向轴承、十字头与滑道之间相互之间的运动状态。
本文分别模拟并比较了活塞杆为刚性体和柔性体时活塞的径向偏心轨迹。结果表明,活塞杆为刚体时,活塞向上行程中,其主要偏向x负半轴,当向下行程时,活塞主要偏向x正半轴。当活塞杆为柔体时,活塞在整个行程中,始终主要偏向x的正半轴,偏心轨迹呈现为“8”字型,能更加准确地反映出活塞在气缸中的偏心运行轨迹。
[1]冯全科,张义云.迷宫压缩机中迷宫泄漏流动泄漏计算与实验研究[J].西安交通大学学报,1997,31(5):97-101.
[2]王玲娣.迷宫压缩机中活塞与活塞杆的振动[J].压缩机技术,1991,(2):5-9.
[3]董新宇,王世杰.迷宫式往复压缩机活塞杆导向支承系的稳定性分析[J].制造业信息化,2014,(2):64-67.
[4]李玉艳,戴晓洲.基于ANSYS的迷宫压缩机活塞杆振动分析[J].压缩机技术业信息化,2011,(2):55-58.
[5]张劲夫,许庆余.考虑运动副间隙的机构动力学研究方法[J].机械科学与技术,2000,(9):22-24.
[6]K.Graunke.Dynamic Behavior of Labyrinth Seals in Oilfree Labyrinth-piston Compressor.Proceedings of the 1984 International Compressor Engineering Conference.Purdue,USA,1984:7-12.
[7]ENZO G,FABIL F,GUIDO V,et al.Simulation of Cylinder Valves for Reciprocating Compressors[C].//Proc.Biennial ASME Conf.,American Society of Mechanical Engineers,2006:1-10.
[8]郁永章.往复活塞压缩机[K].西安交通大学能动学院,2006.
[9]Yucel,U.Kazakia,J.Y.Calculation of Rotor-dynamic Coefficients for Straight-through Labyrinth Seals.Dev.Theor. Appl.Mech.XXI(SECTAM),2002:99-108.
[10]戴大海.磁悬浮轴承数字控制器的研究与设计[D].南京:南京航空航天大学机电一体化,2006.
[11]BaiZhifeng,Liu Shuqin.Research of the Displacement Sensor on Magnetic Bearing[C].The 6th International Symposium on Test and Measurement,Dalian,China,2005.
Research on Piston Assemble Precise Guiding Technology of Labyrinth-piston Compressor-Dynamic Behavior Analysis of Piston-assemble
CHENG Jun-ming,ZENG Xiang-jun,YU Xiao-ling,FENG Quan-ke(School of Energy and Power,Xi′an Jiaotong University,Xi'an 710049,China)
Pistons of labyrinth piston compressors generally run eccentrically in cylinders.In order to avoid the friction between the piston and the cylinder mirror,the radial clearance between them is usually set as 0.2mm to 0.5mm.However,the big clearance value like this could lead to serious leakage and low efficiency,which is the biggest obstacle in labyrinth piston compressor development.Therefore,the paper firstly studied the piston-assemble motion on foundation of multi-body dynamics theory.The simulation respectively under conditions of the rigid and flexible piston rod was carried out.The eccentric orbit of the piston was obtained.This will provide theoretical basis for the accurate centering technology of the piston-assemble in further.
labyrinth piston compressor;piston-assemble motion;multi-body dynamics;leakage
TH457
A
1006-2971(2015)05-0001-05
程军明(1985-),男,甘肃天水人,博士,主要从事往复迷宫压缩机活塞组件精确定心技术的研究。E-mail:chengjunming@stu. xjtu.edu.cn
2015-01-10
