冰箱冷藏室温度场和流场的数值模拟与结构优化
2015-10-27吕传超崔振科王乐
吕传超*,崔振科,王乐
(1-上海贝洱热系统有限公司,上海 201206;2-上海三电汽车空调有限公司,上海 201206)
冰箱冷藏室温度场和流场的数值模拟与结构优化
吕传超*1,崔振科2,王乐1
(1-上海贝洱热系统有限公司,上海 201206;2-上海三电汽车空调有限公司,上海 201206)
采用CFD数值模拟计算的方法,对现有冰箱冷藏室的温度场和速度场进行了计算,并借助实验验证了所采用的数值计算模型的适用性。在此基础上提出了不同壁面温度分布的其他3种方案。当采用冷藏室整个后壁温度分布从上到下逐渐变大的方案时,与现有的市场上采用的主流方案相比,较大的改善了冷藏箱内温度场的均匀性,为冰箱冷藏室蒸发器的设计提供了参考。
冰箱;冷藏室;数值模拟;优化
0 引言
随着生活水平的提高,冰箱已成为生活中必不可少的家用电器[1-3]。冰箱中食物的保存质量直接依赖箱内的空气流场和温度场分布,耗电量也同其内部温度场的分布场密切相关。若箱内温差太大,就会造成放在高温部分的食物过早变质,而低温处的食物可能被冻坏。在耗能方面,箱内温差过大会使得开停机间隔时间缩短,加剧开停机损失,耗能因而增大[4]。随着冰箱容量的大型化发展,这种因箱内温差过大造成的问题将会更加突出。因此对冰箱内温度场和流场研究变得非常重要,许多学者对此做了研究。
吴小华等[5]通过对上冷藏室下冷冻室结构冰箱和上冷冻室下冷藏室结构冰箱室内温度场和流场的数值模拟,发现相对于上冷藏室下冷冻室冰箱而言,上冷冻室下冷藏室结构冰箱冷冻、冷藏室内温度分布更均匀合理;之后吴小华等[6]用FLUENT软件对网状和平板状搁物架的冰箱冷藏室内的温度场和流场分别进行了计算,结果发现,采用平板式搁物架,并使其与蒸发器所在后壁面之间保持2 cm~3 cm间距的形式,既能减小各层内部的温度又能增强换热,是一种比较合理的结构。傅烈虎等[7]用实验和数值模拟相结合的方法得到了箱体内温度场和流场的实际分布及其影响因素。孟祥兆等[8]用粒子图像速度场仪系统结合数值模拟的方法对间冷式冰箱冷冻室的速度场进行了研究,发现顶层间室送风射流有利于阻隔环境传入的热量;中间层左右对称的送风口中心流速的差别约为 28%,将造成间室内温度分布严重不均匀;底层送风口存在明显的射流短路现象。孟祥麒等[9]对斯特林超低温冰箱的温度场和漏热量进行分析,提出了减少漏热的措施。李成祥等[10]分别模拟了冷藏箱开机15 min强制对流和停机3 min自然对流时箱体内流场与温度场的分布情况,为改进箱体风道结构以及送回风方式做出初步探索。
本文通过实验的方法验证了数值计算模型的正确性的基础上,对不同壁面温度分布的温度场和速度场进行了计算,提出了一个优化方案。
1 冷藏室物理模型的建立
本文研究的冰箱冷藏室为直冷式,蒸发器嵌入在冷藏室后壁内部夹层中,位于后壁的上半部。冷藏室内部由两层金属网分为3部分。冷藏室内部空间尺寸为:左右宽 50 cm,前后深度为 40 cm,高为68 cm,如图1所示。

图1 冰箱冷藏室三维模型示意图
当冰箱开机运行时,后壁内置式蒸发器散发的冷量使冷藏室后壁降温,致使壁面附近的空气温度降低。考虑到温度对空气密度的影响,被冷却的空气密度增大,在重力作用下,相对于原来的平衡位置向下运动。未被冷却的空气相对于平衡位置向上运动。这就构成了冷藏室内部冷量的传递,这种热量传递方式称为自然对流,流动方式为浮升力驱动的流动。
2 数学模型
2.1基本假设
为建立数学模型,减小数值计算的计算量,对此物理问题做以下假设。
1)冷藏箱内空气为牛顿流体。
2)冷藏箱持续运行处于正常工作状态下,整体的流动及换热为稳态。
3)三维立体模型简化为二维几何模型,几何模型如图2(a)所示。冷藏箱内的三个隔室是用金属网构成的,考虑到对冷藏箱内自然对流换热影响较小,故对其忽略不计。简化后的冷藏箱几何模型如图2(b)。
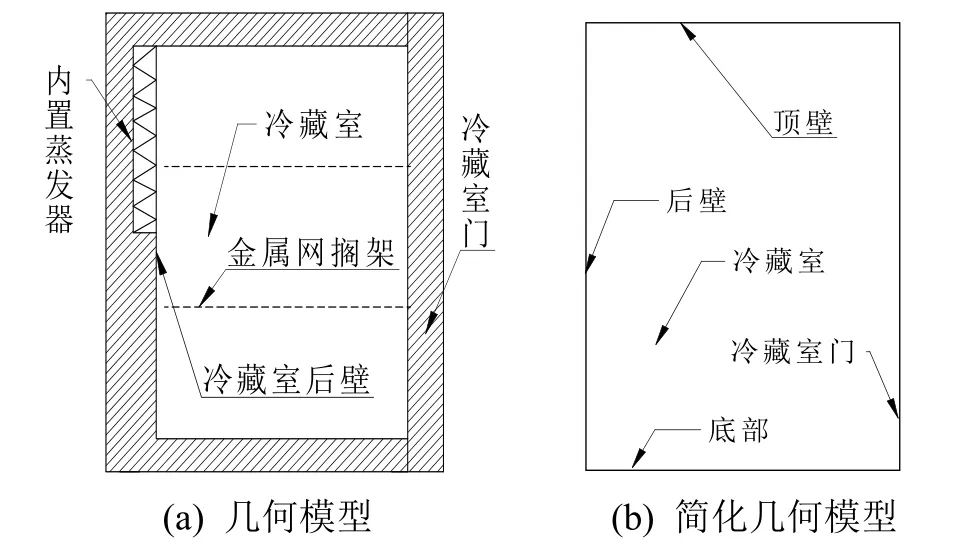
图2 冷藏室几何模型
4)由于冷藏箱各表面间温度温度差值相对较小,因此,忽略内部各表面之间的辐射换热。
5)门封处不漏热。底部为绝热面,这是由于冷藏室底部隔层与冷冻室相连,无热源,故可视为底部为绝热。
6)冷藏室内空气在固体内壁面上满足无滑移条件。
7)冷藏室内空气流动形式为稳定层流。
8)忽略冷藏室内空气的相变过程。
9)对冷藏室内空气流动与换热采用Boussinesq假设,即忽略流体中的粘性耗散项。除密度外,其他物性均为常数。对于密度仅考虑动量方程中与体积力有关的项,其余各项中的密度也作为常数处理。
在自然对流的物理模型中,浮力引起的流动强度可通过瑞利数来判定。

式中:
g ——重力加速度;
β ——热膨胀系数;
ΔT ——对流换热温差;
L——特征长度;
ρ——密度;
μ ——动力粘度;
α ——热扩散率。
在本物理模型中,由于温度变化范围较小,上式可以近似表示为:

以上方程组联立可得β=0.003628,Ra=6.6×108<1010,空气并未达到湍流。
与体积力有关项的密度为:

式中:
0ρ——参考密度;
T0——参考温度。
2.2控制方程
1)连续方程
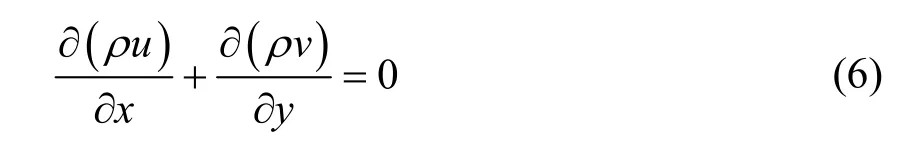
2)动量方程
X方向上:
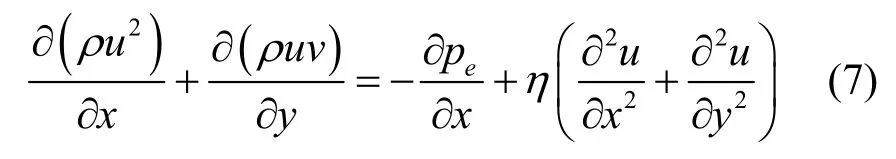
Y方向上:
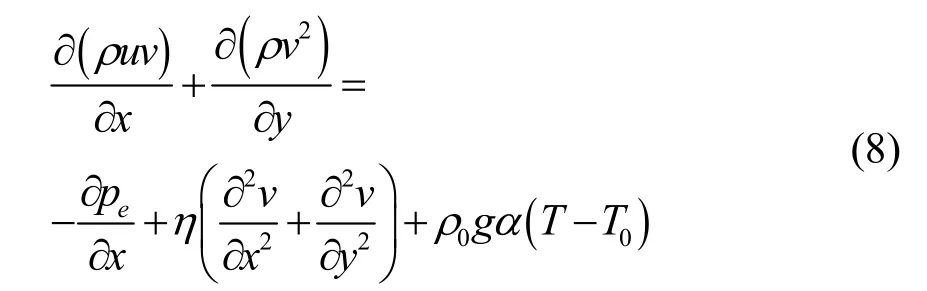
3)能量方程
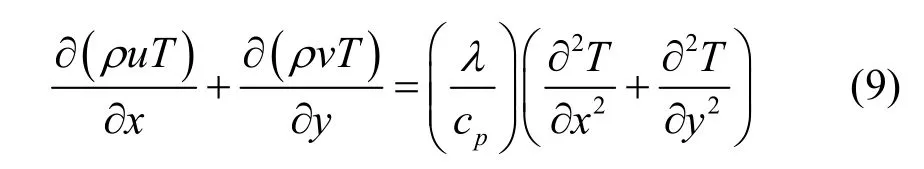
式中:
η——空气的粘度;
cp——为空气定压比热容;
λ——为空气导热系数;
pe——为有效压力(又称折算压力)。
P为绝对压力。
3 数值计算与实验验证
3.1网格划分
本CFD数值模拟采用ANSYS软件中的ICEM划分网络。ICEM具有强大的网格划分功能,可输出100多种求解器所支持的文件格式,处理好的网格文件可直接导入到FLUENT软件中进行计算。网格如下图3,它的长度L=0.4 m,高度H=0.68 m。

图3 冷藏室二维结构化网格
3.2边界条件
1)流动边界条件:取壁面处速度无滑移边界条件,即所有固体表面上流体的速度等于固体表面的速度,因此有在各个壁面处:u=v=0。
2)热边界条件:结合实验实测值,冷藏室各壁面可分为两种类型温度边界条件,分别为第一类边界条件和第二类边界条件。冷藏室后壁上半部、顶部及门为第一类边界条件,温度分别为-8 ℃、5 ℃、3 ℃。后壁下部和底部为绝热边界条件,即q=0。
3.3实验验证
为了验证数值计算结果的正确性,测出了垂直于底部中点(x=0.2 m)竖直方向上(y坐标方向)的8个点的温度,用于和数值计算的结果作对比。其对比结果如图4。
就所测8个点而言,除去上壁面的边界条件上的1点外,其他7点的计算值与实验值的温度差值最小为0.8 ℃,最大为2.5 ℃,平均差别为1.5 ℃。这种差别的来源可能有以下几点。
1)本模型认为冷藏室内的空气为透明体,不吸收辐射的能量,各壁面之间的辐射换热也忽略不计。
2)忽略了门封处的漏热。这一点从图中的数据也可以看出:在竖直高度上,数值计算值在冷藏室的底部和接近顶部位置的与实验值差别稍大,而在冷藏室的中间位置差值较小些。
3)三维模型简化为二维模型,因此不可避免的忽略了冷藏室左右壁面对室内温度的影响。同时,在数值计算时也忽略了冷藏室内中间金属网隔层的影响。
4)数值模拟自身的近似性与实验实测值自身的误差。
所有以上因素(除第 4点外)都是造成 CFD数值模拟温度偏低的原因,从理论上推算,数值模拟的值要比实验实测值小。从图4中可以看出理论计算值始终位于实验测试值得下方,在一定程度上也说明了以上分析的正确性。
对于工程上来说 1.5 ℃以下的温差值已在可接受范围内。况且,在整体趋势上数值计算值与实验实测值是保持一致的,这就更验证了本模型在工程设计中的适用性。
从结果中可以看出,无论是实验值还是数值计算值多数都在0 ℃以下,而相关标准中规定冷藏箱中的温度需在0 ℃~10 ℃之间,这样就超出了相关标准中的规定,这主要是因为在机组运行时选择最高位挡的缘故,数值模拟的边界条件也是按此工况下来设置的。
4 冷藏室的结构优化
4.1不同方案介绍
在验证了本研究所提出的CFD数值计算模型适用性的基础上,模拟了不同后壁温度分布对冷藏室内部温度场、流场分布的影响,以期获得最优方案。
由于冰箱的蒸发盘管置于后壁夹层中,直接影响后壁温度的分布,故本研究的目的也可视为是探讨不同蒸发盘管分布对冷藏室温度的影响。
通过实测实验用冰箱的后壁发现其温度分布为:后壁上半部分在整个测试时间内的平均温度为-8 ℃,后壁下半部分温度与冷藏室内水平方向上空气温度一致,故认为后壁下半部分为绝热壁面。此方案为市场上的采用的主流方案,本文中称为方案1。其温度分布示意图如图5(a)。图示中箭头的长短表示温度绝对值的大小,箭头方向朝右表示温度为零下。图中后壁上半部温度分布恒为-8 ℃。
本文另外提出的三种方案分别如下。
方案 2:整个后壁温度分布不随高度变化,恒为-8 ℃。
方案 3:整个后壁从上到下温度逐渐变大,呈线性分布。分布函数为 T=-11.75y。最高处温度为-8 ℃,最低处温度为0 ℃。
方案 4:整个后壁温度为二级分布。后壁上半部的温度分布称为第一级温度分布,从上到下温度由-8 ℃逐渐升高至0 ℃,呈线性分布,分布函数为:T=-23.529y;后壁下半部的温度分布称为第二级温度分布,第二级的温度仍然是从上到下由-8 ℃逐渐升高到 0 ℃,呈线性分布,分布函数为:T=-23.529y+8。
以上各方案的温度分布都是以蒸发温度为一定的情况下进行拟设的,因此蒸发温度反映到不同方案中各个壁面上时均为-8 ℃。所有温度分布函数中,y的单位为m,T的单位为℃。
此3种方案的温度分布示意图见图5(b)~(d)。

图5 4种方案中冷藏室后壁温度分布示意图
4.2数值计算结果分析
本研究提出的3种方案中,方案2为定壁温温度边界条件,方案3和方案4为变壁温的温度边界条件,在进行数值计算时对于变壁温的温度边界条件要按照温度分布函数编制 UDF程序,然后导入到FLUENT中进行计算。其他边界条件及假设与主流方案中CFD数值计算采用的相同。
4.2.1温度场分布
经计算,其温度场分布如图6所示。图6(a)为市场上采用的主流方案的温度场分布(方案 1)。冷藏室底层部分为-4 ℃左右,中部大部分温度处于-3 ℃与0 ℃之间,1 ℃至5 ℃的温度主要集中在冷藏室顶层,这个温度区间内空气层的平均高度约为5 cm。除壁面空气薄层外,整个冷藏室中最低温度为-4 ℃,位于底部。顶部与底部最大温差为9 ℃,主体温差为4 ℃(除顶部高温集中层外)。
图6(b)图中的方案2其底部温度为-6 ℃左右,从下到上温度逐渐升高至4 ℃,温度分层十分显著,整体温差为 10 ℃,这种温度分布在冷藏室结构设计中是应该避免出现的。这种温度分布下冷藏箱保鲜性能不好,且在使用当中耗能较多。
图6(c)图中方案3的温度场从底部至接近顶部处温度一直处在-1 ℃,只有距顶部大约10 cm处才出现1 ℃的温度层。这种壁面温度分布方式几乎使整个冷藏室呈现出均匀分布的温度场,80%以上的冷藏空间的温差在1 ℃以内,只有在靠近顶部时出现了2 ℃的温差,温度场分布均匀性较之市场上采用的主流方案(方案1)有了很大提高。
图6(d)中的方案4下半部分温度在-2 ℃左右,上半部分在3 ℃左右,这两个温度区域的中间部分出现了大约 5 cm厚度的温度梯较大的温度带。主体温差在5 ℃,其温度分布均匀性不及现今市场上广泛采用的方案1。

图6 四种方案在不同后壁温度条件下的温度场分布
为了更清楚的显示各方案温度在竖直方向的分布情况,比较了x=0.2 m处不同方案的竖直方向上的温度值,其数值模拟值曲线分布图如图7所示。
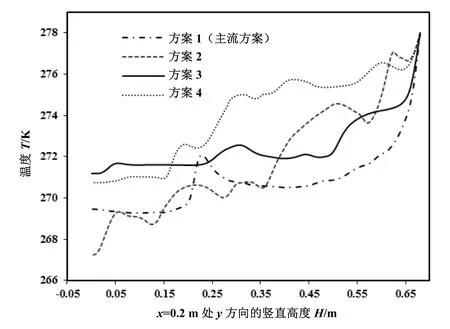
图7 各方案x=0.2 m处竖直方向上的温度分布曲线
图中可以清楚地看到,方案 3的温度曲线在(0~0.52)m的高度之间是最为水平的,整条曲线在(0~0.65)m 的高度之间始终在(-2~1)℃的范围内(271 K~274 K),温差为 3℃。而现今的主流方案在(0~0.65)m的高度之间温度范围为(-4~1)℃,温差为5 ℃。方案2和方案4在温度场分布上与方案1和方案3相比,不占优势。
4.2.2速度场分布
速度场分布主要影响冷藏箱内所放物品降温速率,当冷藏箱内空气流速较大时可以提高冷空气与物品的换热系数,若所放物品能够叫较快达到与箱内的平衡温度,就可以减少冷藏箱压缩机的运行时间,从而节约耗电。
对比图8四种方案下的速度场可以发现,方案2和方案4中0.03 m/s~0.14 m/s的空气流分布面积显然较方案1和方案3的少,再加上从上面对温度场的分析可知,此两种方案在冷藏箱的设计当中不可取。
对于市场上广泛采用的方案1,除壁面处的空气流速外(物品不能靠壁面放置,因为壁面温度较低,物品靠近壁面极易冻坏),0.03 m/s~0.14 m/s的空气流速占到了整个冷藏室的1/2。在方案3中0.03 m/s~0.14 m/s的空气流速所占空间与主流方案接近,主要分布在底部。二者相比并无明显优劣之分。

图8 4种方案在不同后壁温度条件下的速度场分布
综合以上温度场和速度场分析,可以发现方案3要优于其他3种方案。
5 结论
本文采用 CFD数值模拟计算与实验相结合的方法,对冰箱冷藏室的温度场和速度场进行了研究分析,得到结论如下。
1)数值模拟值与实验值温度差值最小0.8 ℃,最大为 2.5 ℃,平均差别为 1.5 ℃。在数值高度方向上,数值计算值与实验实测值整体趋势保持一致。验证了所选模型在工程设计中的适用性。
2)冷藏室后壁上半部分为-8 ℃,下半部分为绝热的方案中主体温差为 4 ℃;空气流速为0.03 m/s~0.14 m/s的流场占到了整个冷藏室的1/2。
3)冷藏室整个后壁温度分布为-8 ℃的方案的主体温差为 10 ℃。空气流速为 0.03 m/s~0.13 m/s的流场占整个流场空间的1/5。
4)冷藏室后壁温度分布为 T=-11.75y的方案的主体温差 1 ℃,温度场最均匀。空气流速为0.03 m/s~0.14 m/s的流场占到了整个冷藏室的1/2。此方案整体上优于当前市场上广泛采用的方案。
5)后壁温度分布为T=-23.529y和T=-23.529y+8的方案的主体温差为5 ℃。速度场分布均匀性不及当前市场上的主流方案。
为实现冷藏室后壁温度分布为T=-11.75y的方案,在冷藏室内壁盘管的设计时,可考虑把盘管设计成由下到上逐渐变密的形式。
[1] 马一太, 梁兆惠, 卢苇, 等. 我国冰箱行业节能的必要性和可行性[J]. 制冷技术, 2004, 24(1): 40-43.
[2] 梅勤光. 家用冰箱的节能减排技术[J]. 制冷技术, 2008, 28(4): 12-14.
[3] 于楠, 丁国良, 赵丹, 等. 用于直冷式和间冷式家用冰箱性能预测的数学模型[J]. 制冷技术, 2011, 31(4): 23-27.
[4] 丁国良, OELLRICH L R. 冰箱箱内空气温度场与流场的优化研究[J]. 制冷学报, 1998, 17(1): 22-27.
[5] 吴小华, 吴业正, 曹小林. 冰箱室内温度场和流场的仿真及结构优化[J]. 制冷学报, 2004, 25(1): 36-38.
[6] 吴小华, 张璟, 宋春节. 冰箱冷藏室温度场和流场的仿真与优化[J]. 北京石油化工学院学报, 2006, 14(3): 8-11.
[7] 傅烈虎, 丛伟, 李青冬. 冰箱内温度场与流场数值模拟[J]. 制冷, 2008, 27(1): 75-80.
[8] 孟祥兆, 俞炳丰. 间冷式冰箱冷冻室粒子图像速度场测量和数值模拟[J]. 西安交通大学学报, 2008, 42(3): 323-327.
[9] 孟祥麒, 祁影霞, 王子龙, 等. 斯特林超低温冰箱箱体设计及箱体内温度场分析[J]. 制冷技术, 2015, 35(3): 34-38.
[10] 李成祥, 陈建东, 李娜, 等. 冷藏箱温度场的数值模拟及其优化[J]. 制冷技术, 2015, 35(3): 39-43.
Numerical Simulation of Temperature and Velocity Fields in Fresh Food Storage Compartment and Structure Optimization for Refrigerator
LÜ Chuan-chao*1, CUI Zhen-ke2,WANG Le1
(1-Behr Thermal Systems Co., Ltd., Shanghai 201206, China;2-Sanden(Shanghai)Automotive Air-Conditioning Co., Ltd., Shanghai 201206, China)
The temperature and velocity fields in the fresh food storage compartment of a refrigerator were conducted with numerical method of computational fluid dynamics(CFD), and the correctness of the numerical calculation model used in this paper was verified by experiment. Based on the numerical model, the other three schemes with different wall temperature distributions were proposed. The equality of the temperature field was greatly improved compared to the existing commercial solutions when the scheme that wall temperature increasing from the top to the bottom was adopted, which provides reference for the evaporator design of the fresh food storage compartment of the refrigerator.
Refrigerator; Fresh food storage compartment; Numerical simulation; Structure optimization
10.3969/j.issn.2095-4468.2015.05.204
*吕传超(1988- ),男,助理工程师,硕士。研究方向为:制冷系统测试及优化。联系地址:上海市浦东新区陇桥路355号。邮编:201206。联系电话:18818252941。E-mail:lvccusst@163.com。
