有限长线声源斜面声场分析∗

张赵晶　沈　勇　吴浩东　刘紫赟

（南京大学声学研究所　近代声学教育部重点实验室　南京　210093）

⋄研究报告⋄

有限长线声源斜面声场分析∗

张赵晶沈勇†吴浩东刘紫赟

（南京大学声学研究所近代声学教育部重点实验室南京210093）

为了进一步研究有限长线声源的声场特性，完善有限长线声源声场理论，建立了有限长线声源斜面声场的模型，提出了其理论计算方法。基于仿真结果和数据分析，探讨并得到了有限长线声源斜面声场特性的三个参数与斜面声场特性之间的关系。通过调整斜面倾角α、交点的位置r0以及有限长线声源的长度L，可以有效改善斜面声场的分布。

有限长线声源，声场特性，斜面声场

1　引言

扬声器线阵列是声频领域的研究热点之一［1-7］。在理论研究时，常用“线声源”替代“线阵列”。无限长连续线声源可以辐射柱面波，在距离加倍时声压级衰减3 dB。而点声源辐射球面波，在距离加倍时衰减为6 dB［8］，该观点被大量引用。实际上，现实中的扬声器线阵列都是有限长的，柱面波模型不完全适用，这一点常被忽视。故研究有限长线声源的辐射声场很有意义。目前，Ureda［2-7］等人已经开展了扬声器线阵列的理论研究，并给出了对于不同类型的扬声器线阵列的几种基本声场模型及其分析，包括扬声器线阵列的指向性和辐射特性等问题。沈勇等通过使用一种交错排列的波导有效的改善了扬声器线阵列的辐射［1］。但这些理论和研究中都未提及对线阵列所在空间的斜面声场的研究分析，而与实际最相关的正是斜面上的声场分布情况。本文通过研究线阵列中最具代表性的有限长线声源模型的声场特性，建立了一维斜线模型，并通过一维模型获得了其斜面声场模型。基于斜面声场模型，分析了有限长线声源斜面声场的情况，得出了有限长线声源的斜面声场特性，并总结了影响斜面声场的三个主要参数（斜面倾角α、斜面与线阵列中心轴线交点r0以及线声源长度L）与声场特性之间的关系。本文的研究结果对于进一步分析线阵列的声场特性具有重要意义。对于一些大型场馆的设计，如体育馆、音乐厅等，坐席大多以斜面分布，与本文探讨的情况相同，本文得到的结论对这些场馆的设计与改进具有指导作用。本文讨论的线声源为直线型均匀线声源。

2　有限长线声源模型建立与分析

如图1所示，有限长线声源长度为L，中心点O距参考轴上接收点A的距离为r［3］。

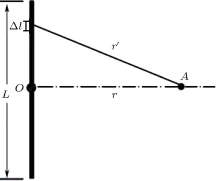
图1　长度为L的有限长线声源模型Fig.1 Finite line sound source module（length=L）

将有限长线声源分割为大量的、无限小的线状辐射源［3，9］，有限长线声源在A点辐射的声压p（r）为

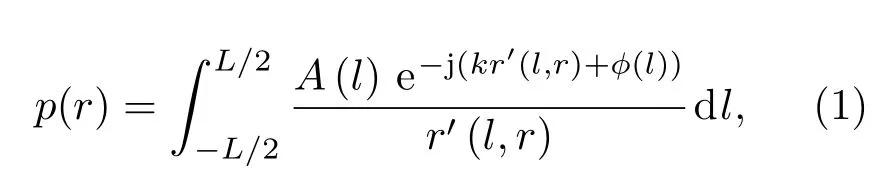
式中r′（l，r）为A点到辐射单元的距离，k为波数，A（l）为l相关的幅度函数，ϕ（l）为l相关的相位函数。在均匀线源中，归一化：A（l）=1，ϕ（l）=0，有

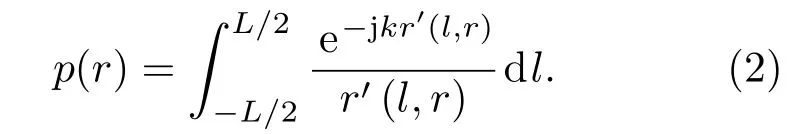
2.1斜线声场模型

为建立斜面声场模型，首先考查其一维情况。考虑平面xOz中的直线m上的声压，建立斜线声场模型如图2所示。

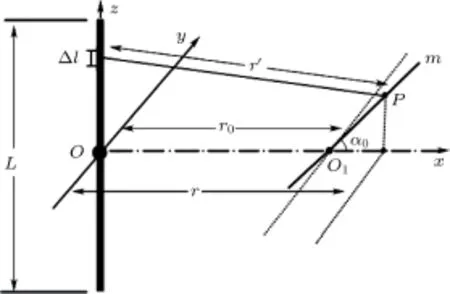
图2　长度为L的有限长线声源斜线声场模型Fig.2 Slant module of finite line sound source（length=L）

设直线m与x轴夹角为α0（0≤α0≤2π），m与中轴线交点O1至线声源中点O的距离为r0，m上一点P在x轴上的投影到线声源中点O的距离为r，P到辐射单元Δl的距离为r′，则P点的声压可以表示为

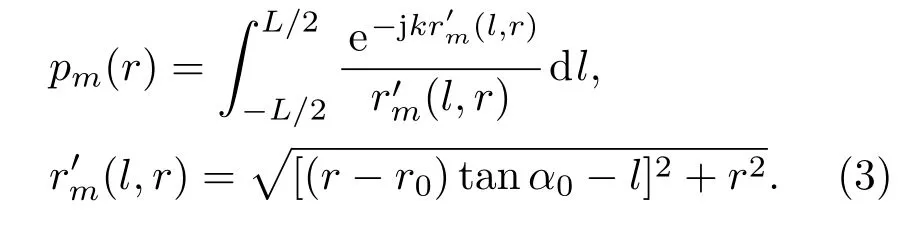
2.2斜面声场模型

（1）考虑平面xOy上任意一点（xa，ya，0）处的声压，r为点（xa，ya，0）到原点的距离，rα为线阵列上的某个辐射单元Δl到点（xa，ya，0）的距离，可以得到线阵列在点（xa，ya，0）产生的总声压为

（2）考虑平面xOz上任意一点（xa，0，za）处的声压，r为点（xa，0，za）到原点的距离，rβ为线阵列上的某个辐射单元Δl到点（xa，0，za）的距离，可以得到线阵列在点（xa，0，za）产生的总声压为

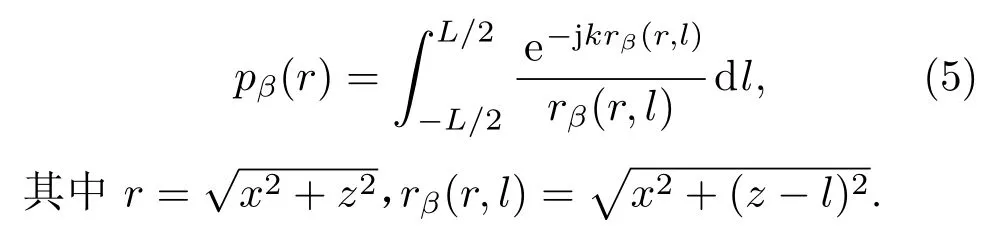
（3）考虑垂直于平面xOz的直线所在平面Ω上的声压（平面Ω与平面α夹角不为π/2），建立如图3所示的斜面声场模型。

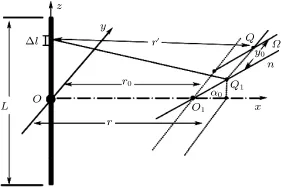
图3　长度为L的有限长线声源的斜面声场模型Fig.3　Slope module of finite line sound source（length=L）

设平面xOy与平面Ω的夹角为α0（0≤α0≤2π，α0/=π/2），平面Ω上某一点Q到辐射单元Δl的距离为r′，考虑平面xOz与Ω的交线n，Q到n的距离为y0，n与中轴线的交点O1至线声源中心O的距离为r0，过Q点作垂直于n的直线n1，交点为Q1，Q1到线声源的距离为r，则Q点处的声压可以表示为

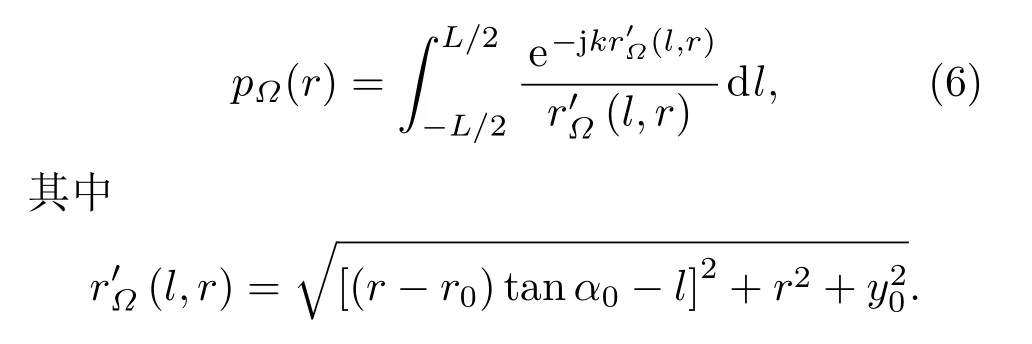
（4）考虑平面yOz的平行面上的声压（即平面Ω与平面xOy夹角为π/2的特殊情况），设平面Ω与x轴交点为x0，平面Ω上一点S的坐标为（x0，y，z），则S点的声压为

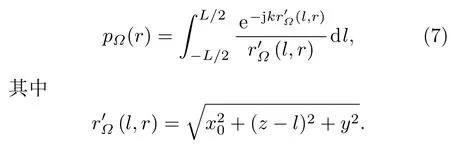
3　声场模拟及分析

由理论推导得到的有限长线声源的声场公式，对其声场分布进行分析，通过声场仿真来直观的展示分析结果。为了能够与Ureda的结果［2］对比，此处设有限长线声源长度L为4 m，频率f为8 kHz，声速c0取344 m/s2。

（1）考虑xOy平面上的声场分布，得到线声源在xOy平面上的直达声声场仿真图，如图4所示。xOy平面也即斜面倾角为0°的特殊情况，与图6（a）对比具有一致性，同时验证了斜面仿真的准确性。

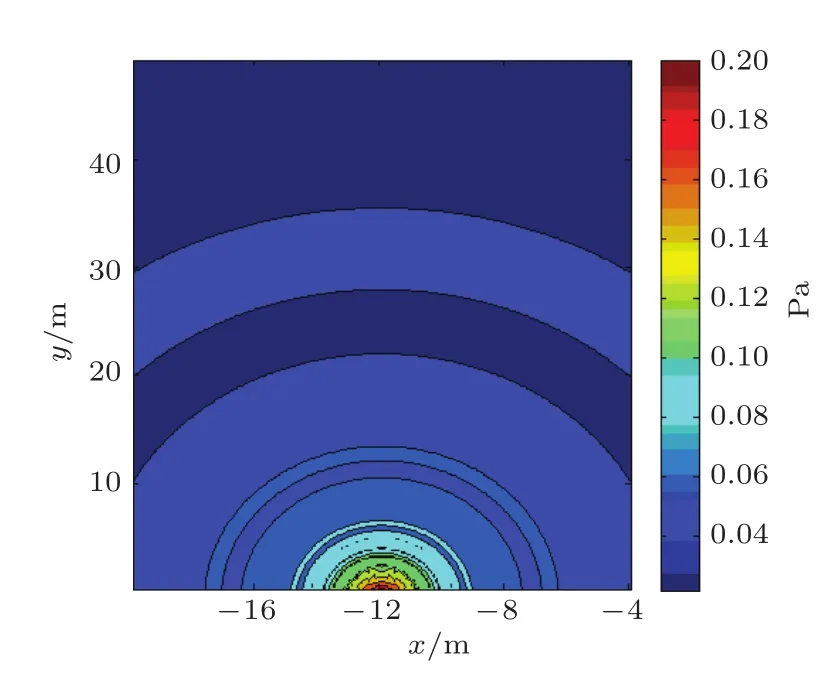
图4　xOy平面直达声声场仿真图Fig.4 Simulation of direct sound in xOy plane

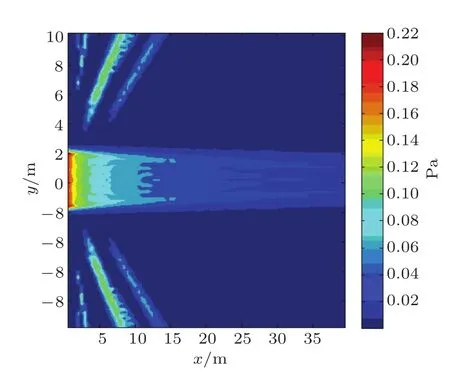
图5　xOz平面直达声声场仿真图Fig.5 Simulation of direct sound in xOz plane

（2）考虑xOz平面上的声场分布，得到线声源在xOz平面上的直达声声场仿真图，如图5所示。可以发现有限长线声源在该方向具有较强的指向性，符合其辐射特征。

（3）考虑斜面Ω上的声场分布，分别改变斜面倾角α、交点r0的位置以及有限长线声源的长度L来考察对斜面Ω声场分布的影响。

以15°为间隔，分别对α角从0°至45°的情况进行了仿真分析，如图6所示（其中r0=5 m）。

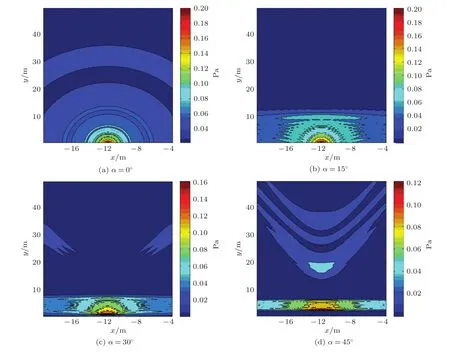
图6　α角为0°、15°、30°和45°时斜面Ω的声场分布情况Fig.6 Sound field distribution in slope Ω（α=0°、15°、30°and 45°）

从图6对斜面声场的仿真中发现，当r0=5 m时，随着α角的变大，在斜面Ω上r0附近相比于周边区域具有较强声压级的声场区域（以下简称为r0附近的声场区域）逐渐变窄，且在y=［15，50］m的区域中出现了新的不均匀声场区域，并向r0所在位置靠拢。当α角确定时，如令α=30°，改变r0，使r0分别为5 m、15 m、30 m和60 m，对斜面Ω进行模拟，如图7所示。

由图7发现，r0的取值不大时，r0附近的声场区域具有不均匀性；当r0的取值逐渐变大时，r0附近的声场区域趋于均匀。另外，当r0变大时，线声源附近即y=［0，10］m附近的不均匀区域向r0靠拢。

改变有限长线声源的长度L，考察L对斜面声场的影响。为方便对比，令α=30°，分别取L=4 m、L=6 m和L=8m，得到斜面Ω上的声场分布，如图8所示。

由图8（a）、8（b）和8（c）发现，当线阵列的长度L增加时，r0附近的声场区域也变逐渐大，这符合有限长线声源在其垂直方向具有较强指向性的特点。在图8（c）中，发现r0附近的声场区域和线声源附近y=［0，10］m的不均匀区域开始有重叠，这与之前对图7的分析结果相符。对于L=8 m，使r0的取值变大，令r0=30 m，得到如图8（d）所示的声场分布图。图8（d）中可以发现r0附近的声场区域又再次变得均匀，但是覆盖区域的范围并无明显变化。

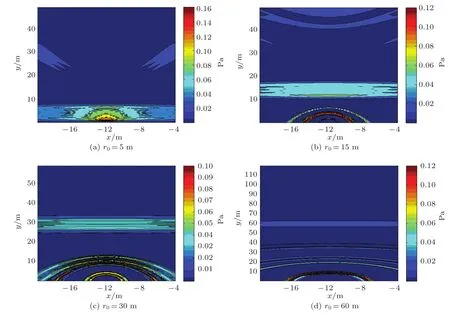
图7　r0分别为5 m、15 m、30 m和60 m时斜面Ω的声场分布情况Fig.7 Sound field distribution in slope Ω（r0=5 m、15 m、30 m and 60 m）

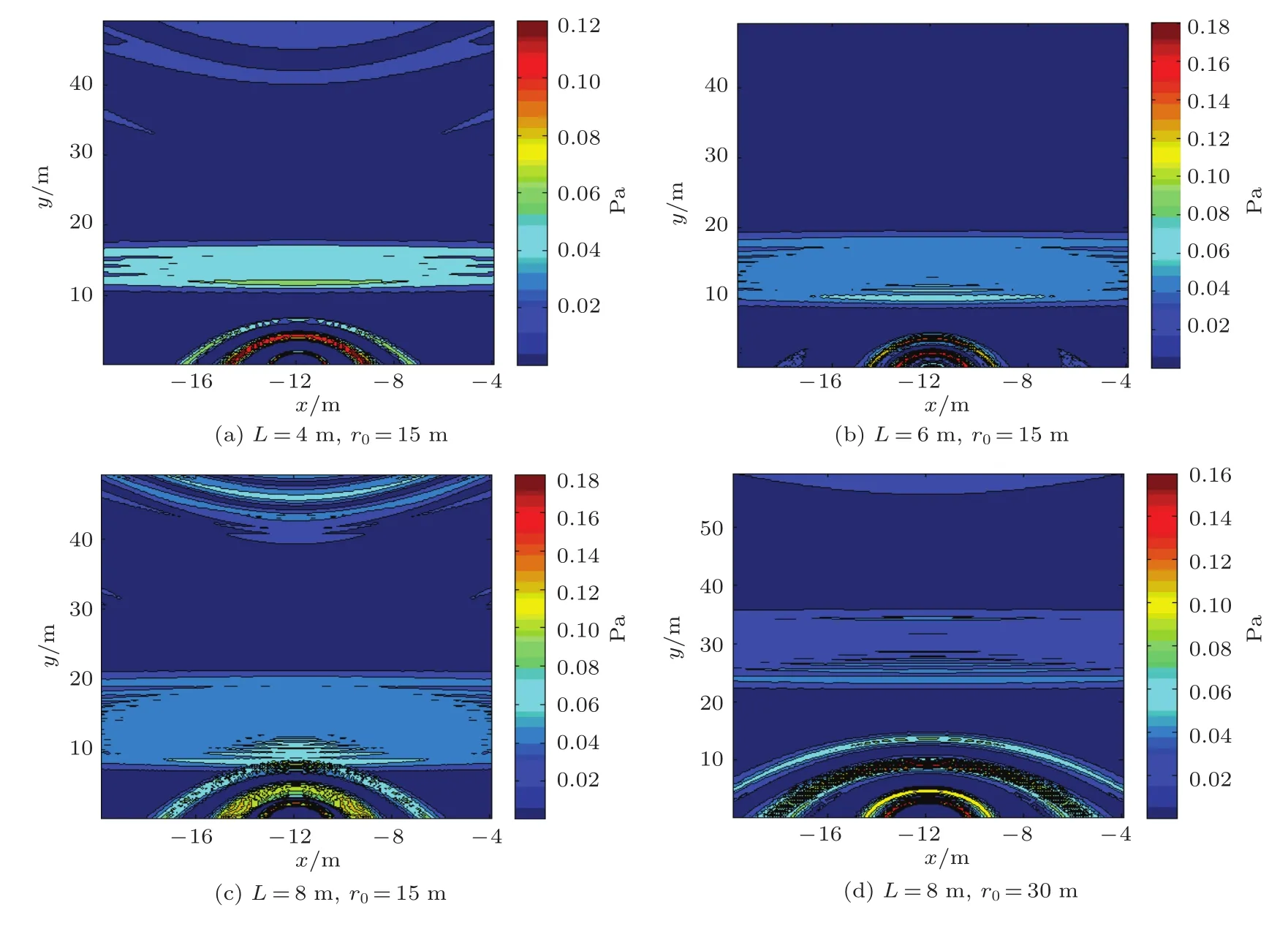
图8　有限长线声源长度L对斜面Ω声场的影响Fig.8 Sound field distribution in slope Ω with different L

4　结论

本文通过对有限长线声源的研究，建立了有限长线声源的斜面声场模型，提出了对有限长线声源斜面声场分布进行分析的方法，进一步完善了线阵列的相关理论。通过分别改变斜面倾角α、交点r0的位置以及有限长线声源的长度L，讨论了对于不同α、交点r0以及线声源长度L，有限长线声源所在空间斜面声场的变化情况，得到如下结论：

（1）斜面倾角α较大（α大于30°）时，有限长线声源的辐射覆盖区域相对较小，声场均匀度较差；

（2）线声源长度L确定、r0取值较小时，r0附近区域的声场均匀度较差；

（3）线声源长度L增加时，有限长线声源的辐射覆盖区域变大。因此，通过调整斜面倾角α、交点r0的位置以及有限长线声源的长度L，可以有效改善斜面声场的分布。本文提出的斜面模型及其分析方法也可应用于其他类型的线阵列。

［1］AN K，SHEN Y，LE Y.Improving the response of loudspeaker line arrays by a staggered arrangement of highfrequency waveguides［J］.J.Audio Eng.Soc.，2010，58（10）：828-837.

［2］UREDA M S.Analysis of loudspeaker line arrays［J］.J. Audio Eng.Soc.，2004，52（5）：467-495.

［3］UREDA M S.Pressure response of line sources［C］//Audio Engineering Society Convention 113.Audio Eng.Soc.，2002.

［4］UREDA M S.Line arrays：Theory and applications［C］//Audio Engineering Society Convention 110.Audio Eng.Soc.，2001.

［5］BUTTON D.High frequency components for high output articulated line arrays［C］//Audio Engineering Society Convention 113.Audio Eng.Soc.，2002.

［6］KLEPPER D L，STEELE D W.Constant directional characteristics from a line source array［C］//Audio Engineering Society Convention 14.Audio Eng.Soc.，1962.

［7］AHRENS J，SPORS S.Sound field reproduction using planar and linear arrays of loudspeakers［J］.IEEE Trans. Audio Speech Lang.Process.，2010，18（8）：2038-2050.

［8］杜功焕，朱哲民，龚秀芬.声学基础［M］.南京：南京大学出版社，2001：316-318.

［9］沈勇.扬声器系统的理论与应用［M］.北京：国防工业出版社，2011：175-176.

Research on slope sound field of finite line sound source∗

ZHANG ZhaojingSHEN Yong†WU HaodongLIU Ziyun
（Key Laboratory of Modern Acoustics，MOE，and Institute of Acoustics，Nanjing University，Nanjing 210093，China）

To further research of the finite line sound source,the slope sound field module was built and a method on analysis of slope sound field was proposed which is significant to theoretical research and practical application on finite line sound source.Through simulation and data analysis,the influence to the slope sound field caused by three parameters—slope angle,location of the intersection,and length of finite line sound source, which are related to the slope module is discussed.The relationship between three parameters and slope sound field was concluded.The slope sound field characteristics can be improved by choosing appropriate parameters.

Finite line sound source,Sound field characteristics,Slope sound field

O42

A

1000-310X（2015）01-0001-06

10.11684/j.issn.1000-310X.2015.01.001

2014-04-10收稿；2014-06-14定稿

∗有限长近似线声源声学特性研究（A040509），舞台听觉呈现系统声场仿真技术研究（2012BAH38F03-02）

张赵晶（1989-），男，江苏苏州人，硕士研究生，研究方向：声学。

E-mail：yshen@nju.edu.cn