基于最小二乘法的均匀扩声技术研究∗

刘力　蔡野锋　吴鸣　杨军

（中国科学院声学研究所　噪声与振动重点实验室　北京　100190）

基于最小二乘法的均匀扩声技术研究∗

刘力蔡野锋吴鸣杨军†

（中国科学院声学研究所噪声与振动重点实验室北京100190）

针对目前室外及超大型室内空间的扩声应用中声场分布不均匀的问题，本文提出了一种基于最小二乘法声场重建方法的扩声技术。该技术通过对目标声场的逼近来计算线性扬声器阵列各通道的输入参数，实现扩声区域内声压级的均匀分布，同时约束非扩声区域的声能量以获得较好指向性。本文通过仿真研究算法各参数的改变对控制结果的影响，探讨不同扩声区域和目标所对应参数的选取方法。仿真和实验比较了该算法以及未经控制的声场、相移法波束控制的效果，证明该方法可以获得更好的声场均匀度。

最小二乘法，均匀扩声，扬声器阵列

1　引言

在广场演出、体育场扩声和大型户外庆典等室外扩声应用，以及火车站、机场航站楼等超大型室内空间的扩声中，扩声系统往往需要覆盖很长的距离。而由声波的扩散及环境影响导致的声压级衰减使得近远场的扩声效果难以兼顾［1］，远处听众获得较好听音效果时，扬声器附近的声压级将过高而令人难以忍受，这一问题对扩声系统的声场均匀度提出了较高的要求。此外，由于室外存在着各种噪声，扩声区域周围建筑物会产生反射声，因此需要扬声器有很好的指向性，在增强直达声的同时减弱反射声的影响［1］。与此类似，在火车站等百万立方米级别的超大型室内空间中，混响时间最长可以达到十几秒［2-3］，这也需要声源有良好的指向性，通过增强直达声来提高扩声时的语言清晰度。

在现有的扩声系统中，通常使用扬声器阵列和高指向性扬声器单元来解决声场分布不均匀、信噪比低的问题。使用弓形或J形扬声器阵列可以兼顾近远场效果［4］：这些阵列的直线部分有着高指向性，可以进行远场声能量投射和直达声增强，而弯曲部分则可使近场声能量均匀分布。通过对音箱和号筒技术的改进，增强扬声器单元的指向性［5-6］，可以实现更为精确的声能量投射。这些都是使用物理方法改变阵列结构和单元声学特性来改善扩声效果，但在设备固定后就不方便进行移动或调整，无法根据目标区域的变化动态调整扩声效果。针对这一缺点，近年来出现了指向性可调的线性扬声器阵列产品［7］。这些阵列通常使用相移法波束控制技术，通过改变阵列各通道的延时来调整波束偏转角［7］，实现扩声区域的动态调整。但通过相移法获得的声场存在着波动较大的缺陷，在中心部分声压级较高，两侧衰减迅速，整体声压级分布不均匀。除此以外，对扬声器阵列扩声性能进行优化的方法也得到了广泛的应用。如基于菲涅耳原理对阵列辐射波阵面进行优化的波阵面修正技术［8］，以及类似的数字几何控制（Digital and geometric radiation control）［9］技术等。原本用于水下换能器的CBT（Constant beamwidth transducer）理论也被应用于扬声器阵列扩声，它可以产生宽度不随频率改变的声波束［10］。此外，基于SINC函数理论、二次剩余序列（QR）［11］以及遗传算法［12］等优化方法的研究，可以获得更为均匀的扬声器阵列辐射声场和较大的辐射功率。但这些方法都是针对扬声器阵列本身的辐射特性进行优化，没有根据实际的扩声环境进行调整。

本文研究基于扬声器阵列的均匀扩声技术，使用最小二乘法声场重建方法调节扬声器单元的输入信号来获取期望声场，实现扩声性能随目标区域变化的动态调整。该方法通过对预设目标声场的逼近来调节线阵列各通道输入信号的幅度与相位，使扩声区域内的声压级在空间上实现均匀分布；同时约束非扩声区域的声能量，提高扩声的能量输出效率并且可以获得更好的波束指向性。

2　基于最小二乘法声场重建的均匀扩声

本节研究基于最小二乘法声场重建技术的均匀扩声方法，包括使用最小二乘法进行声场重建的基本算法以及针对扩声应用的具体做法。

2.1最小二乘法声场重建

如图1所示，考虑存在N个声源的自由声场，在声场中设置M个接收点。

图1　声场中声源和接收点分布Fig.1 Sound sources and receivers layout

设其中第l个声源的输入信号为wl，该声源到第m个接收点的传递函数表示为Hm，l，在第m个接收点上获得的总声压pm可表示为所有声源响应的叠加［13］：

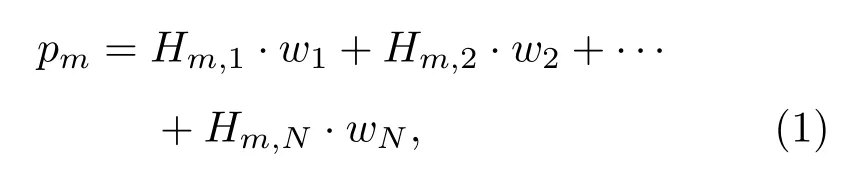
因此所有M个接收点上的声压为

其中p=［p1p2···pm···pM］T，代表所有控制点上的声压，而N个声源的输入表示为w=［w1w2···wm···wM］T，传递函数矩阵H如式（3）所示：

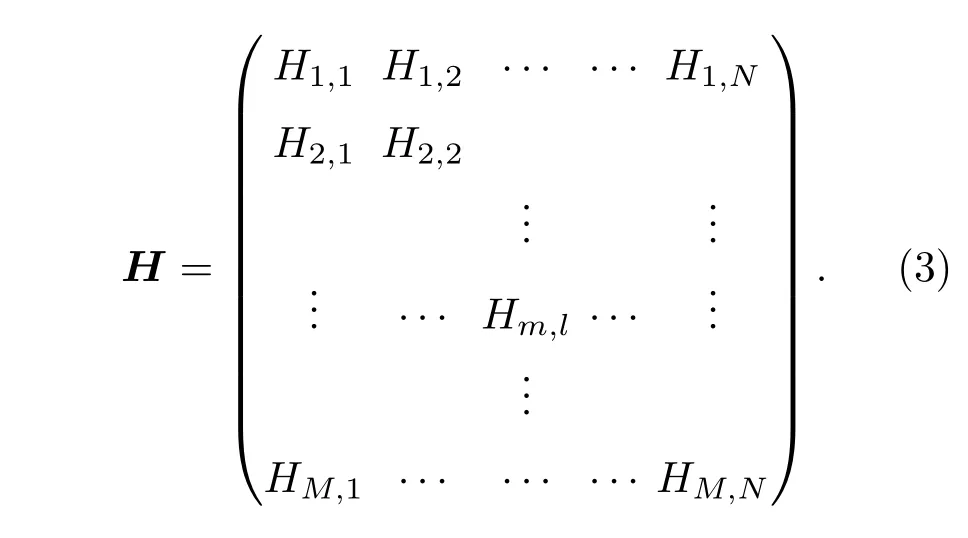
最小二乘法声场重建是通过对期望声场的逼近来实现的，为了计算某个特定声场所对应的权值w，还需要设置期望声场声压级分布d：

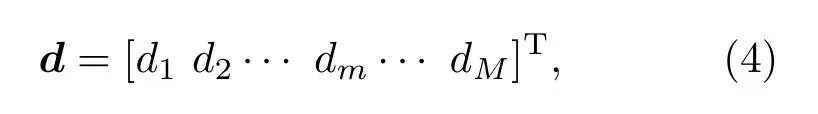
将其带入式（2），可以得到

在式（5）中，由于控制点的数量总是大于声源数量，该式为超定方程组，无法获得w在传统意义上的解析解，因此使用最小二乘法［14-15］进行计算：

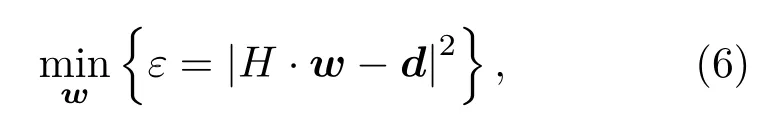
其解为

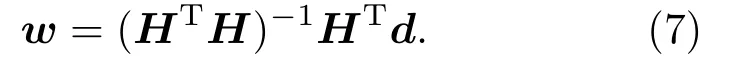
2.2均匀扩声应用

针对均匀扩声应用，本文设计应用场景如图2所示。其中目标区域位于x轴，扬声器阵列位于声场左侧y轴上，中心点距目标区域高度为H1。扩声的目标区域设为x轴上B1～B2这段距离，声场控制的目标是使这一区域内的声压级均匀分布。

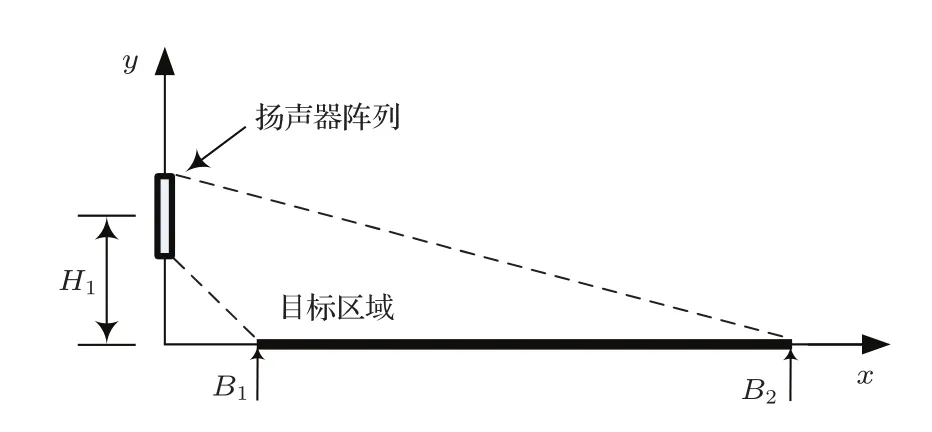
图2　扩声场景设置Fig.2 The sound reinforcement scenario

本文中的扬声器阵列为线阵列，单元个数为N，间距为d，阵列单元使用点声源模型进行仿真。设扬声器阵列第l个单元的位置是则该单元到第m个控制点的距离可以表示为

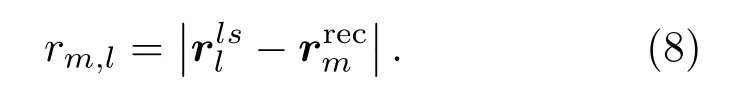
第l个扬声器单元在第m个控制点上产生的响应如下：

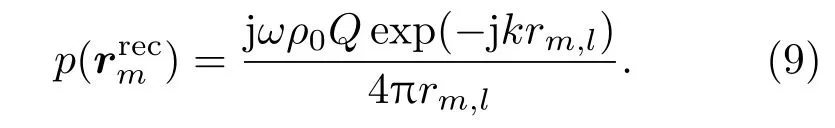
为获得期望的声场，还需在声场中选取控制点并设置合适的目标响应，用以计算对应的扬声器阵列输入参数。声场中控制点的选取如图3所示。首先考虑目标区域的控制点。为获得均匀的声压级分布，设这一区域内控制点上的目标声场幅度相等。而声场的相位以阵列中心为参考点变化，也就是将阵列整体做为一个声源。这一区域的目标声场如式（10）所示，其中代表声场中第m个控制点的位置，rm为该控制点到阵列中心的距离。

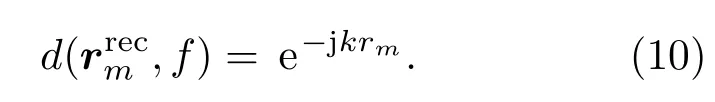
为了使扬声器阵列输出的声能量聚集在目标区域上，从而获得更好的能量输出效率和波束指向性，还需要在目标区域四周再选取部分控制点，称为静音区域。如图3所示，静音区域将目标区域包围住，宽度为B2，高度为H。设这些控制点上目标声场幅度为零，以约束声场中的声能量。

图3　控制点选取示意图Fig.3 Selection of control points

设定好目标声场后即可计算出对应的扬声器阵列输出参数。本文首先设置一个基本仿真参数，并在其基础上研究算法各相关参数的变化对控制结果产生的影响。这里仿真该参数下算法在目标区域的声场均匀效果，并与相移法进行比较。

基本参数设置如下：控制区域高度H为15 m，目标区域起点B1为10 m，终点B2为50 m，所有控制点均匀分布，间距为0.1 m。扬声器阵列单元数为16个，间距d为0.2 m，阵列如图2所示，中心点位于y轴并与x轴垂直，高度H1为7 m，约为静音区域高度的一半。为避免栅瓣的影响，仿真的声波频率设为1 kHz，此时最小二乘法获得的总声场的相对声压级分布如图4（a）所示。同时给出相移法获得声场的相对声压级分布图，波束主瓣中心轴与x轴的交点设为目标区域的中心（x轴上35 m处），对应的波束偏转角约为11°，结果见图4（b）。

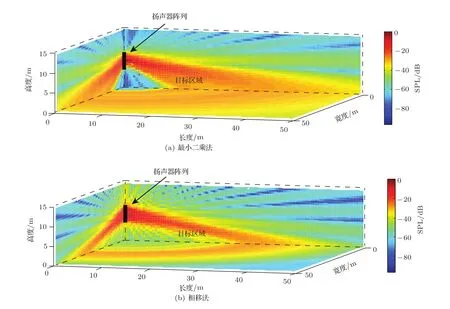
图4　两种方法获得的声场分布Fig.4 SPL distribution obtained by two different methods

为方便比较，这里对仿真中获得的声压级均匀区域进行定义，设其为x轴上声压级与目标区域最大声压级的差值小于3 dB的区域。两种方法在目标区域的声压级分布情况如图5所示，其中加粗线条表示两种方法各自获得的声压级均匀区域。

图5　目标区域声压级分布Fig.5 SPL distribution on the target area

图中可以看到，最小二乘法在目标区域获得了更为均匀的声压级分布，声压级波动范围在6 dB以内，获得的声压级均匀区域长度约为32.80 m。而相移法在主瓣中心处声压级较高，声压级最高部分与较低部分相差15 dB，获得的均匀区域长度为13.20 m。因此最小二乘法在声压级分布的均匀度上占有优势。

3　算法参数的影响

本节通过仿真研究各参数的改变对算法结果的影响，探讨不同扩声区域和扩声目标对应参数的选取方法。主要研究扬声器阵列的相关参数，目标区域的选取和控制点间距的影响，同时与相移法控制的结果进行比较。

3.1扬声器阵列相关参数的影响

仿真中扬声器阵列的单元间距将影响栅瓣出现的频率，间距0.2 m时栅瓣将在1.7 kHz左右出现。而阵列长度会影响近远场的临界距离，阵列长度为3 m，声波频率1 kHz时近远场临界距离为26 m。

3.1.1阵列单元的数量和间距

这里仿真比较了不同的阵列单元数量（阵列单元数从4个逐渐增加到32个）对扩声效果的影响，同时研究了阵列单元的间距与声波波长对算法结果的影响，仿真了间距为0.2 m，0.13 m，声波频率为1 kHz，1.55 kHz时的扩声效果，结果如图6所示。

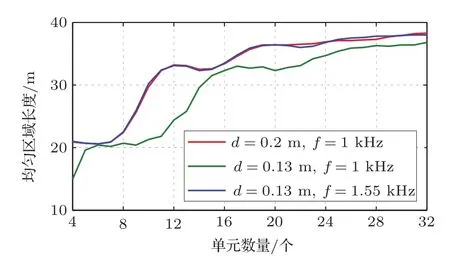
图6　阵列单元数量和间距及声波频率对均匀区域长度的影响Fig.6 Length of the uniform region against the element number with different spacings and frequencies

在间距不变的情况下，阵列单元数量的增加可以使获得的均匀区域长度增长，较多的单元使声场重建的效果更为精确；另外在阵列单元数量较少时，增加其数量获得的均匀区域增长较为显著，单元数量较多时均匀区域的增长较为缓慢。因此在实际应用中，出于成本的考虑，需要根据实际的扩声场景选择阵列的单元数量。

仿真结果还表明，阵列单元间距对算法效果的影响体现在它与声波波长的比值上，这一比值的减少会使均匀区域的长度缩短，而比值相同时获得的扩声效果也基本相同。因此下一步可以研究激活的阵列单元之间的距离随频率变化的算法。

3.1.2阵列的高度和倾斜角

实际应用中需要考虑阵列的安装高度和摆放角度，本小节将探讨两者对扩声效果的影响。设阵列倾斜角为θ，这里仿真了θ从0°向80°增大，以及H1逐步增长的情况下均匀区域长度的变化。同时为了避免阵列倾斜导致的重建误差，对声场上下方静音区域的选取方式进行修改，如图7所示。

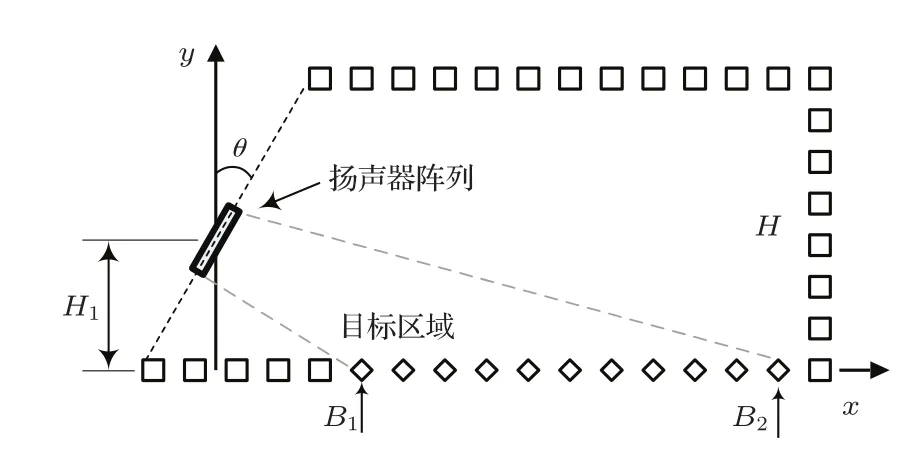
图7　阵列倾斜放置时的控制点选取Fig.7 Selection of control points when the array is tipped

仿真时需要根据阵列的高度对静音区域控制点的高度H进行调整，避免对阵列上方声场能量的过度压制。H1为7 m时对应的H使用基本仿真参数中的数值，在H1增大后，H的值也进行了适当的增加，具体数值如图8（a）所示。可以看出，H1为13 m时均匀区域长度随阵列倾斜角的增大开始逐渐变长，而倾斜角度增大到7度后均匀区域的长度开始保持稳定，随后在倾斜角度增大到55°时，均匀区域的长度随阵列倾斜角的增大近似线性的缩短。H1的值缩短或者变长时均匀区域长度变化的临界角会随之缩小或增大。在H1为7 m时，均匀区域长度缩小到极限后还会出现反弹现象，均匀区域长度的缩小是由于阵列的倾斜使得声场受到了上方静音区域控制点的压制，而当阵列倾斜角度过大时，相对于地面上静音区域的控制点，声场上方静音区域控制点的数量不再占有优势，无法再起到抑制声能量的作用。

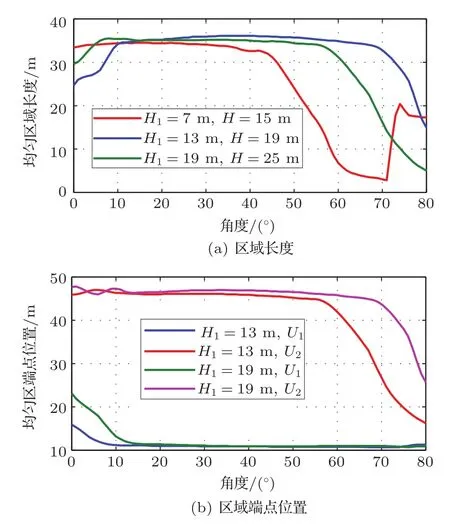
图8　阵列倾斜角及高度对均匀区域的影响Fig.8 Array inclination angle against the uniform region with different heights

再观察H1发生变化时均匀区域的起始点和终止点的情况，为方便表述，设图5中加粗线条表示的均匀区域左侧起点为U1，右侧终点为U2。仿真结果如图8（b）所示，可以看到在H1为13 m和19 m，阵列倾斜角小于10°时，U1的值无法达到最接近B1的程度。此时只有在阵列向下倾斜的角度增大，波束整体左移时，U1才会达到其最小值。因此算法对阵列波束进行偏转的角度是有限制的，阵列倾斜角变化时均匀区域的长度改变都是这一限制所导致的，同时目标区域左侧起始点B1的取值也将受到其影响。

由仿真结果可知，在实际扩声应用中，阵列安装时的角度和高度都会在一定程度上受到扩声区域位置的限制。阵列安装的倾斜角度受到的限制较少，在一定范围内都可以获得好的扩声效果。而在阵列安装高度过高并且期望获得较好的近场扩声效果时，则需要对其安装角度进行调整。

3.2目标区域的选取

3.2.1目标区域的近场起点

目标区域左侧起始点B1受到阵列波束最大偏转角的限制，因此研究该点最佳位置的选取需要知道波束偏转的具体限制角度。仿真时将B1移动到原点，即B1=0 m，同时提高H到25 m。

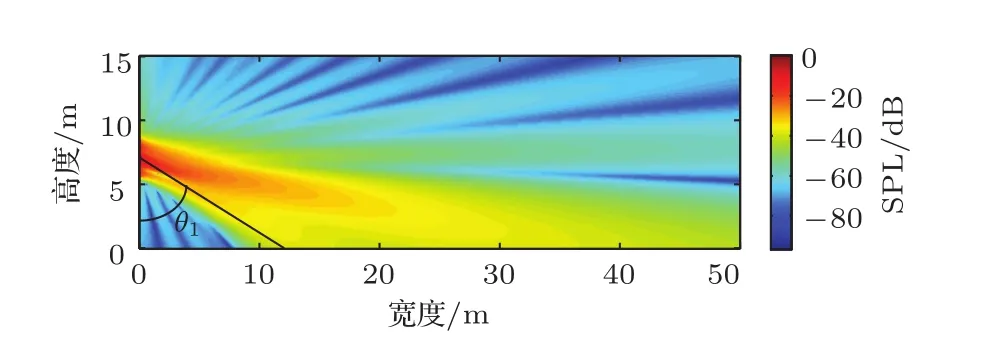
图9　角度位置示意图Fig.9 Position of the angle

如图9所示，研究算法最终获得的均匀区域左侧起始点U1和扬声器阵列中心点的连线与y轴形成的夹角θ1，仿真这一夹角的大小随阵列高度的变化情况。仿真中保持阵列单元间距d=0.2 m不变，改变声波频率以研究单元间距与声波波长的比值对结果的影响。

仿真结果如图10所示。随着阵列高度的变化，θ1的大小基本保持不变，因此相同频率和阵列单元间距情况下，阵列波束可以偏转的最大角度是不变的。同时随着频率的增大，这一角度也在逐渐增大，因此可以认为该角度的大小取决于单元间距与声波波长的比值。这一仿真结果同样证明了3.1.2节中的结论。因此实际使用中目标区域近场起始点的选取与阵列的高度及安装的倾角有关。

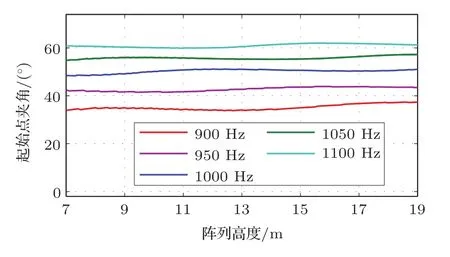
图10　阵列高度及声波频率对均匀区域起点影响Fig.10　Length of the uniform region against array height with different frequencies

3.2.2目标区域的远场终点

为了研究目标区域远场终点的选取，这里仿真了均匀区域长度占目标区域总长度的百分比随目标区域终点位置B2变化的情况。B2的值从20 m到160 m逐渐增长，同时目标区域左侧起始点B1固定为8 m（按照3.2.1的结论），结果如图11所示。

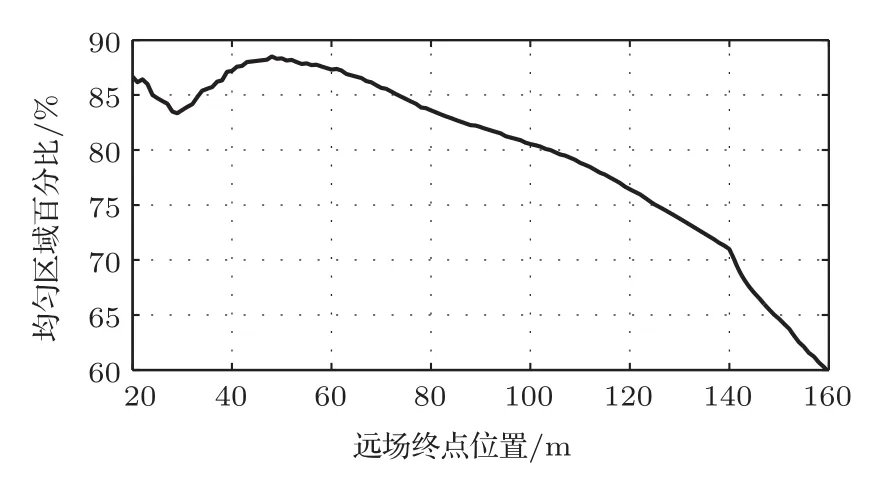
图11　远场终点对均匀区域的影响Fig.11 Percentage of the uniform region length against the far-field endpoint location

B2从20 m逐渐增大到50 m的过程中，声压级均匀分布区域占目标区域的百分比有小的波动，而在B2从50 m到140 m的变化过程中，均匀区域百分比随该点的移动近似线性的降低，140 m后百分比开始迅速下降。B2变化过程中均匀区域长度的百分比主要受到远场声压级衰减的影响，因此实际应用中选择该点时需要考虑它与阵列之间的距离。

3.3控制点的选取

3.3.1整体控制点间距

控制点的间距代表了预设目标声场的精确程度，这里仿真了不同控制点间距下，最小二乘法声场重建在目标区域产生的声压级均匀区域的分布情况，比较了声压级均匀区域的起点U1和终点U2的位置以及均匀区域长度的变化。仿真时的控制点间距取0.1 m、0.2 m、0.5 m和1 m，以保证控制点的均匀分布，消除非整数控制点数量的影响。其他参数都使用基本仿真参数，结果如表1所示。

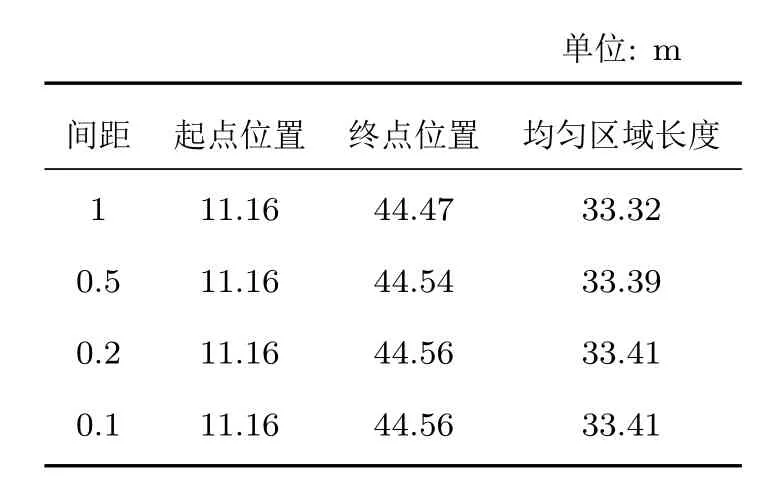
表1　控制点间距的影响Table 1 Effect of control points spacings

随着间距的减小，均匀区域起点位置基本不发生变化，终点位置则随之增大并最终保持44.56 m的值不变。这一变化的产生是由于右侧垂直方向静音区域控制点对其周围声能量的压制，当控制点分布均匀且间距较大时，单个控制点影响的区域变大，声能量向左侧发生偏移。但控制点间距的变化产生的总体影响不大，实际应用中基本可以忽略。因此在应用时可以将控制点间距适当放大，以减少目标区域范围调整时算法的计算量，提高系统的反应速度并降低硬件成本。

3.3.2不同区域控制点间距的调整

考虑声场中静音区域控制点对其附近声场能量的压制作用，尝试增大一部分区域的控制点间距来放宽对这些区域声能量的限制，从而延长声压级均匀区域的长度。这里增加右侧垂直静音区域控制点间距，如图12所示，右侧方框中的圆形控制点表示要修改的区域。

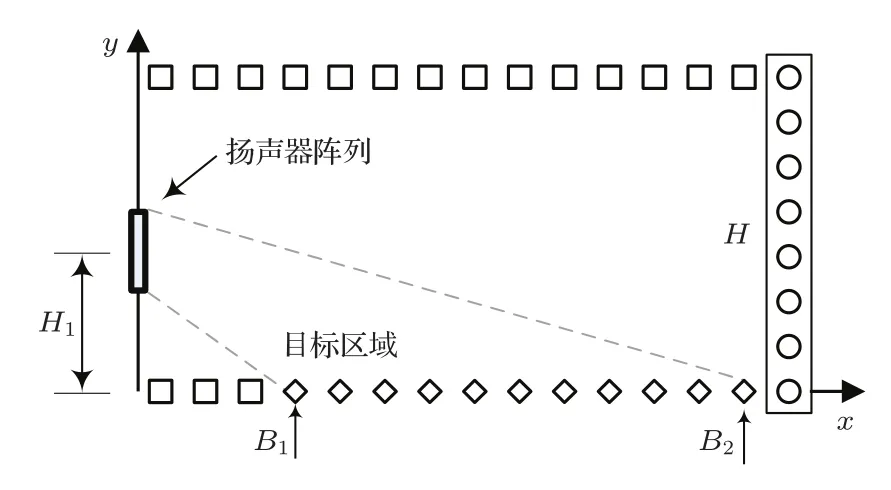
图12　改变右侧垂直边界上控制点间距Fig.12　Control points spacings change in the right edge

仿真时其它区域控制点间距设为0.1 m，右侧垂直部分控制点间距取0.1 m、0.2 m、0.5 m和1 m，目标区域声压级的分布情况如图13所示。可以看出，右侧控制点间距越大时目标区域的声压级分布也会越均匀。当间距为0.5 m和0.1 m时，均匀区域右侧终点U2已经超过了预设目标区域B2的范围，因此这一做法对目标区域声压级的均匀分布有积极作用。

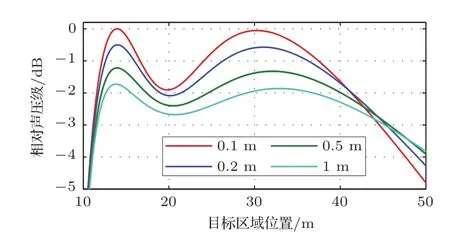
图13　不同右侧控制点间距所对应的目标区域声压级分布Fig.13 SPL distribution in the objective region with different control points spacings in the right edge

但是放宽声场压制的同时也会带来目标区域声能量的降低，间距从0.1 m增大到1 m的过程中，目标区域整体声压级分布会以0.5 dB左右的幅度下降。这是由于声场右侧静音区域控制点间距增大从而导致了声能量向目标区域以外的部分发生扩散。

随后仿真了仅增加右侧下方一部分控制点间距的情况，如图14所示，右侧方框中的圆形控制点表示要修改间距的区域，其高度用H2表示。

设H2范围内控制点间距分别为0.2 m、0.5 m和1 m，仿真了H2从0到15 m的增长过程中算法所获得均匀区域长度的变化情况，结果如图15所示。可以看到，H2在0～7 m范围时，均匀区域长度随着该参数线性增长，间距越大增长的速度也越快。H2增长到7 m后，获得的均匀区域长度基本不变。

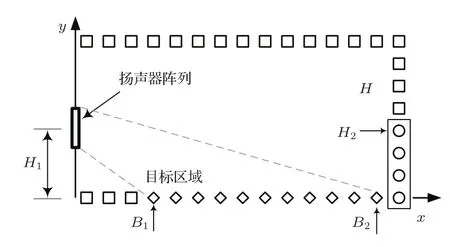
图14　增大右侧部分区域的控制点间距Fig.14　Part of control points spacings in the right edge is increased

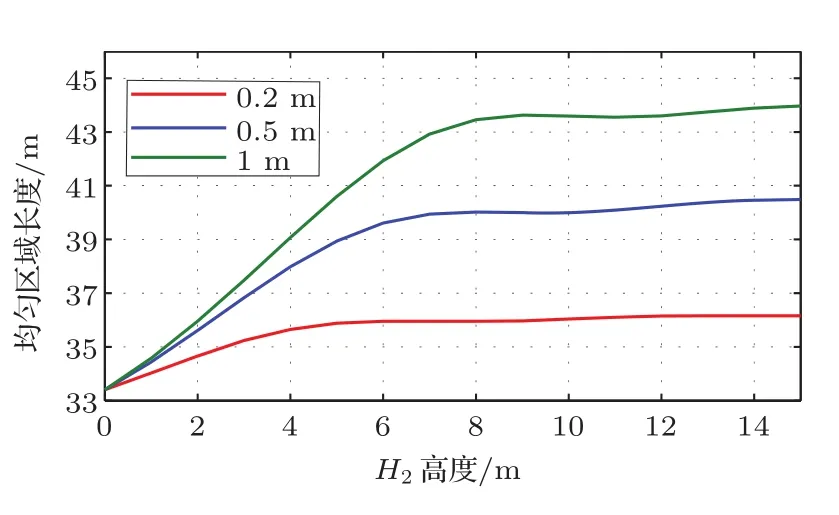
图15　H2高度变化对均匀区域长度的影响Fig.15　Influence on the uniform area length with different H2heights

再次比较延长B2和提高H2这两种可以使均匀区域长度增加的方法，以及它们对目标区域声能量大小的影响，结果如图16所示。可以看到，当获得的均匀区域长度基本相等时，两种方法在目标区域的声压级分布也基本相同，但是相对来说改变H2长度的做法获得的声压级分布更均匀一些。同时可以看到两种方法在增长均匀区域长度的同时也存在一定负面效果，目标区域整体声压级降低了1 dB左右，这也是由于声场右侧静音区域控制点间距增大导致的声能量向目标区域以外部分的扩散。实际应用中，由于均匀区域长度基本随H2的长度线性变化，该参数可以起到精确调节均匀区域长度的作用。同时这一做法在一定程度上可以减少控制点的数量，减少系统的计算量。

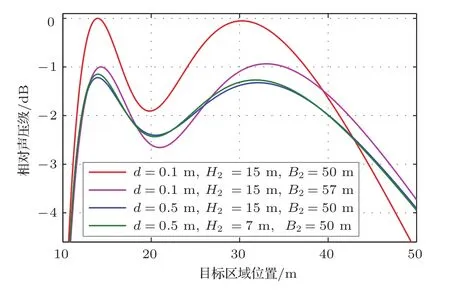
图16　不同H2长度下目标区域声压级分布情况Fig.16 SPL distribution in the objective region with different H2heights

4　实验比较

本节将未经控制的声场及相移法波束控制的结果与最小二乘法声场重建的效果进行了比较，通过仿真和实验验证最小二乘法在扩声应用中的有效性。实验在中国科学院声学研究所的半消声室中进行，受到场地和实验设备的限制，这里将声场宽度缩小为10 m，高度4 m，扬声器阵列单元数量减少为8个，单元间距为0.13 m，阵列中心点距地面高度1.5 m。扩声的目标区域为地面上3～10 m的范围，控制点按照图3进行选取，间距0.04 m。仿真和实验的频率为1 kHz。

首先对未控制的声场，相移法波束控制和最小二乘法控制的声场在实验条件下可以获得的结果进行仿真。相移法产生的波束主瓣中心轴与地面的交点设为目标区域的中心，即地面上6.5 m处，对应的主瓣偏转角度约为13°。相移法和最小二乘法声场重建的总声场声压级分布如图17所示，x轴为地面上的位置，y轴为高度，从图中可以看出由于阵列高度的影响，最小二乘法的优势并不明显，但总体的声场分布还是优于相移法的效果。

三种情况下目标区域声压级的分布如图18（a）所示，x轴为地面上的位置，y轴为相对的声压级。从图中可以看到，未控制时目标区域声压级整体较小，且在10～30 m处有较大波动，波动范围在10 dB左右，这是阵列声场的栅瓣导致的。使用相移法可以将波束的主瓣投射到地面以提高声压级，但波束主瓣区域声压级较高，其余部位的声压级衰减的幅度稍大于10 dB。使用最小二乘法获得的声场最为均匀，声压级分布在5 dB范围内。再比较整体声压级大小，相移法的整体声压级最大，最小二乘法比它低大约5 dB，未控制的声场整体声压级最小。

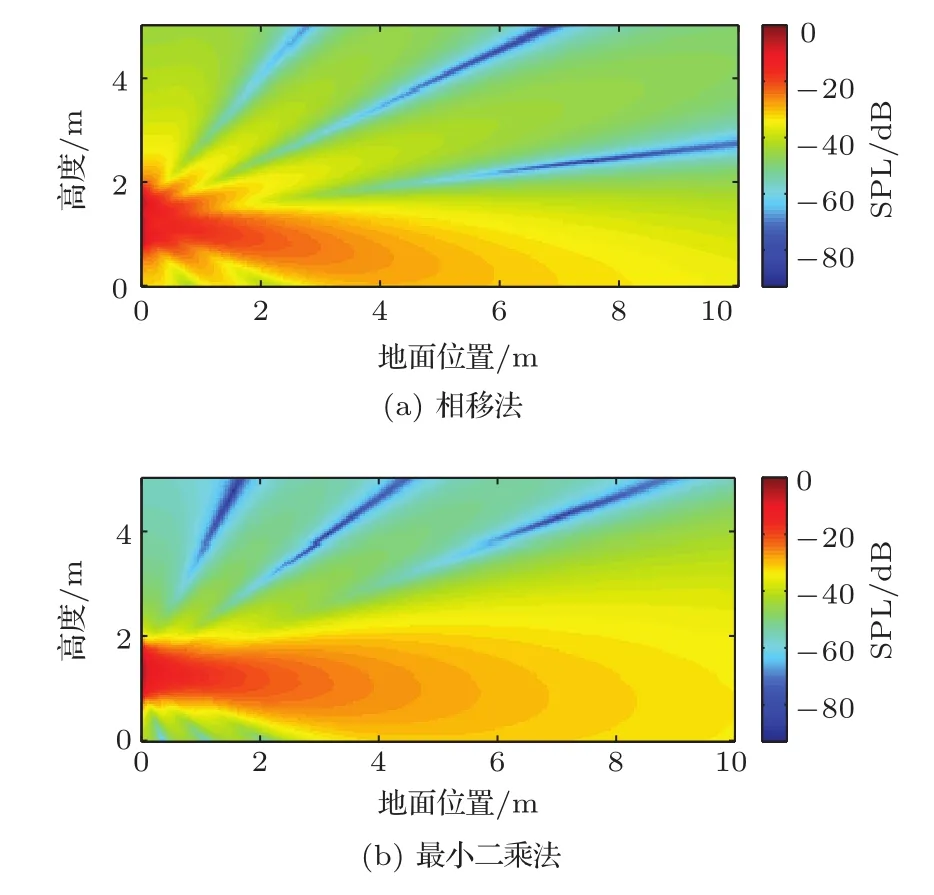
图17　两种方法获得的总声场声压级分布Fig.17　Sound field obtained by two different methods

实验时，使用NI公司的PXI-1042系统产生信号，输出到扬声器阵列，产生的8通道信号经过功放放大后驱动扬声器单元，扬声器单元使用惠威公司的S3W音箱。信号测量使用B&K公司的Pulse 3560C和4189传声器，传声器数量为8个，放置间距为4 cm。为消除地面反射声的影响，在地面铺设了吸声棉。实验时传声器固定不变，移动扬声器阵列的位置进行测量。

实验结果如图18（b）所示。可以看到，未控制的声场声压级最低，并且在约3 m处有一个低谷。相移法控制的声场声压级最高，在3～4 m这段比LS方法高约5 dB。最小二乘法获得的声压级分布最为均匀，声压级整体要比未控制的声场在5～7 m范围内高出约5 dB，实验与仿真结果基本相符。

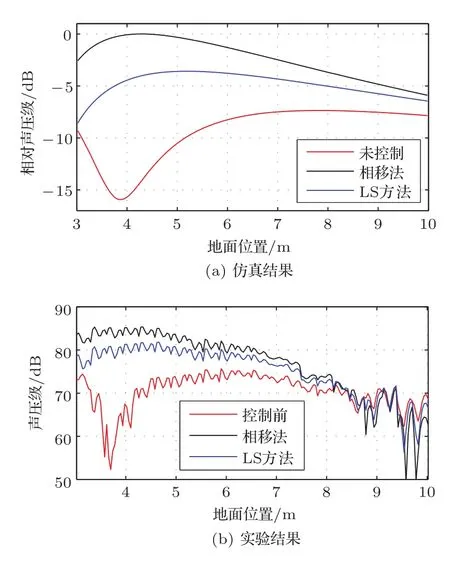
图18　三种情况的目标区域声压级分布Fig.18　SPL distribution in the target region with three different situations

5　结论

针对目前室外及大型室内空间扩声系统存在的缺陷，本文设计并初步实现了一种基于最小二乘法声场重建方法的均匀扩声技术，通过对目标声场的逼近，在扩声的目标区域内实现声压级的均匀分布。本文仿真并分析比较了扩声应用中，算法参数的不同设置方式对最终扩声结果的影响，并探讨了不同的控制点选取方式在实际应用中的作用，同时通过实验将该方法的结果与未经控制的声场及相移法波束控制的效果进行了比较。仿真和实验均证明了该方法可以在扩声区域内获得更好的声场均匀度。

［1］MULLER G，MOSER M.Handbook of engineering acoustics［M］.Berlin：Springer，2009.

［2］MAPP P.The design of a multilayer，time-delay-zoned public address system for a large railway terminal complex［C］.82th AES Convention，1987：2428.

［3］尹力军，叶年发，潘立超，等.铁路车站大空间混响时间的测试与分析［J］.铁路计算机应用，2013，22（5）：37-40，43. YIN Lijun，YE Nianfa，PAN Lichao，et al.Testing and analyzing on reverberation time of huge space in railway station［J］.Railway Computer Application，2013，22（5）：37-40，43.

［4］UREDA M S.Analysis of loudspeaker line arrays［J］.J. Audio Eng.Soc.，2004，52（5）：467-495.

［5］GANDER M R.Fifty years of loudspeaker developments as viewed through the perspective of the audio engineering society［J］.J.Audio Eng.Soc.，1998，46（1/2）：43-58.

［6］SCHUHMACHER A，RASMUSSEN K B.Modelling of horn-type loudspeakers for outdoor sound reinforcement systems［J］.Appl.Acoust.，1999，56（1）：25-37.

［7］王以真，胡秉奇.可控指向性声柱［J］.电声技术，2010，34（6）：17-23. WANG Yizhen，HU Bingqi.Controllable direction column loudspeakers［J］.Audio Engineering，2010，34（6）：17-23.

［8］URBAN M，HEIL C，BAUMAN P.Wavefront sculpture technology［J］.J.Audio Eng.Soc.，2003，51（10）：912-932.

［9］MEYNIAL X.Dgrc arrays：A synthesis of geometrical and electronic loudspeaker arrays［C］.120th AES Convention，2006：6786.

［10］KEELE，D.The application of broadband constant beamwidthtransducer（cbt ）theorytoloudspeaker arrays［C］.109th AES Convention，2000：5216.

［11］沈勇，欧达毅，安康.改善扬声器阵列辐射特性的几种方法［J］.电声技术，2007，31（7）：31-35. SHEN Yong，OU Dayi，AN Kang.Some methods of improving the radiation characteristics of loudspeaker arrays［J］.Audio Engineering，2007，31（7）：31-35.

［12］欧达毅，沈勇，安康.优化扬声器阵列的指向性与声功率级［J］.应用声学，2008，27（2）：125-130. OU Dayi，SHEN Yong，AN Kang.Optimizing directivity and acoustic power level of loudspeaker array［J］.Appl. Acoust.，2008，27（2）：125-130.

［13］KIRKEBY O，NELSON P A.Reproduction of plane wave sound fields［J］.J.Acoust.Soc.Am.，1993，94（5）：2992.

［14］KIRKEBYO.Reproductionofacousticfields［D］. Southampton：University of Southampton，1995.

［15］FAZI F M，NELSON P A.The ill-conditioning problem in sound field reconstruction［C］.123th AES Convention，2007：7244.

An investigation of uniform sound reinforcement technology based on least squares method∗

LIU LiCAI YefengWU MingYANG Jun†
（Key Laboratory of Noise and Vibration Research Laboratory，Institute of Acoustics，Chinese Academy of Sciences，Beijing 100190，China）

The problem to achieve uniform sound pressure level（SPL）over audience area in both outdoor and indoor sound reinforcement applications is investigated in this paper.A novel design strategy based on the least squares method is proposed.The flat distribution of the SPL can be achieved while the input signals of loudspeaker array are adjusted by approximation of the desired response on the audience area.At the same time,the target level on the other positions is kept as low as possible for better directivity control.The impact on the SPL distribution arisen from different parameter settings of this method is evaluated by simulations,and the selection procedure of these parameters is also discussed.A comparison among the effects of the proposed method,phase-shift method as well as the uncontrolled sound field was conducted in real applications.Both simulation and experimental results demonstrate the effectiveness of the new design.

Least squares,Uniform sound reinforcement,Loudspeaker array

O422.2

A

1000-310X（2015）01-0007-10

10.11684/j.issn.1000-310X.2015.01.002

2014-01-23收稿；2014-02-25定稿

∗国家自然科学基金资助项目（11304349）

刘力（1987-），男，江苏南通人，博士研究生，研究方向：信号与信息处理。

E-mail：jyang@mail.ioa.ac.cn