形心导向虚拟力的无线传感器网络部署算法

宋鑫宏， 方 伟， 熊伟丽

(江南大学物联网工程学院，江苏无锡214122)

无线传感器网络(Wireless Sensor Networks，WSNs)的随机部署问题是指如何引导移动传感器节点［1］改变位置实现对监测区域的最大化覆盖。随机部署问题是WSNs研究和应用的关键问题之一，它一方面关系到无线传感器节点能量的有效控制、感知服务质量和整体生存时间;另一方面也关系到网络相关传输、管理、存储和计算的代价［2］。

虚拟力算法［3-4］作为处理覆盖部署问题的有效手段，自提出以来得到了国内外学者的广泛关注。Li等［5］提出了面向目标跟踪的虚拟力算法(Target involved virtual force algorithm，TIVFA)，使传感器节点根据目标位置和重要性程度自动调整网络布局，以改善网络覆盖率和提升目标探测概率;Yu等［6］将Delaunay三角网引入虚拟力算法，定义邻居节点为通信半径内由Delaunay三角网连接的节点，使覆盖率得到提升;Lee等［7］提出了基于泰森多边形形心的部署策略(Centroid-Based Scheme，CBS)，将若干传感器节点覆盖监测区域的问题分解成每个传感器节点覆盖其对应泰森多边形的问题，降低了问题的复杂性;Han等［8］将CBS与传统虚拟力算法结合提出了一种混合部署算法，使障碍物、邻居节点以及泰森多边形形心对传感器节点产生虚拟力从而引导传感器节点移动。但在该算法中，泰森多边形形心对各传感器节点的虚拟力需通过权重值加以限制。由于CBS具有无需设置参数、边界自适应、覆盖率高等优点，文中保留CBS的优点，并与虚拟力算法调整节点间相对位置的能力相结合，提出一种新的基于泰森多边形形心导向虚拟力的部署算法(CBVFA)。

1 无线传感器网络覆盖问题

1.1 问题模型

假设在A×B的监测区域内随机抛撒N个感知半径为r、通信半径为cth的同构无线传感器节点，传感器节点集 S={s1，s2，…，sN}，节点位置 si=(xi，yi)。将监测区域均匀离散化为a×b个目标点，目标点位置 tj=(xj，yj)j∈［1，a × b］。

文中使用使用二元感知模型计算节点si对目标点 tj的感知概率 p(si，tj)［9］。si与 tj的距离记为 d(si，tj)，具体表示为

当 d(si，tj)≤ r时，si覆盖 tj，p(si，tj)记为 1;否则 si未覆盖 tj，p(si，tj)记为0。计算公式如下:

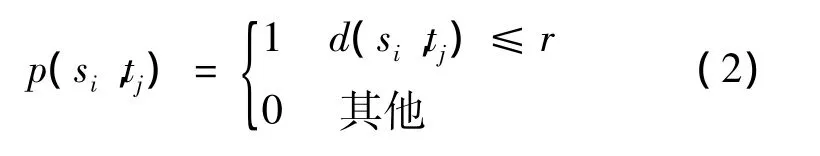
传感器节点集S对目标点tj的感知概率使用联合感知概率Qj表示。在N个传感器节点中若存在一个传感器节点覆盖tj，则tj的联合感知概率Qj为1，否则记为0。联合感知概率表示为

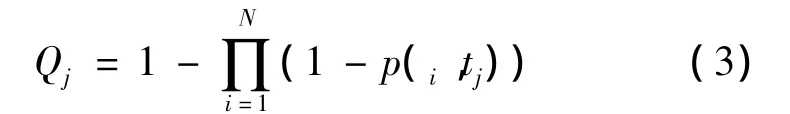
1.2 性能指标

WSNs对监测区域的覆盖情况使用覆盖率CR表示，CR的计算方法为已覆盖目标点之和与总目标点数之比，具体表示为

节点分布均匀性U是衡量网络寿命长短的标准之一，U越小WSNs的分布越均匀，其网络寿命越长。U的计算方法为N个传感器节点与其对应邻居节点距离的标准差取均值［11］，公式如下:

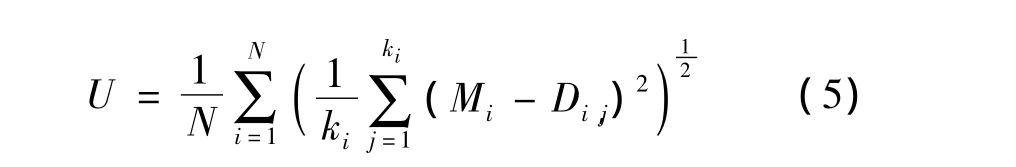
式中:Mi为第i个传感器节点与其所有邻居节点的平均距离;Di，j为第i个传感器节点与其第j个邻居节点的距离;ki为第 i个传感器节点的邻居节点总个数。

2 虚拟力算法与基于泰森多边形形心的部署策略特点分析

2.1 虚拟力算法

虚拟力算法(VFA)将移动传感器节点抽象成虚拟的带电粒子，当节点间的距离小于某一阈值时，节点间产生斥力;当节点间的距离大于某一阈值时，节点间产生引力。某一节点所受的虚拟力为所有邻居节点对其产生作用力的合力。

假设第i，j个传感器节点为si和sj，它们之间的距离为dij，Cth为传感器节点的通信半径，Dth为产生吸引力或排斥力的阈值，通常取r≤Dth≤2r［5］，Fij为传感器节点si受传感器节点sj的作用力。Fij的计算公式［12］如下:

Fi为传感器节点si受到所有传感器节点的合力，具体表示为

其中，aij为传感器节点si与sj的向量角度;wA，wR为权重系数。节点位置更新公式［12］如下，

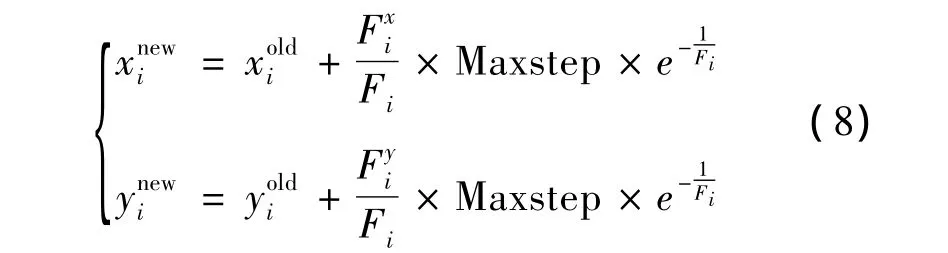
图1为一个无线传感器节点在虚拟力算法作用下的受力情况。其中:s1为当前分析的节点，s2，s3，s4位于s1的通信半径范围之内，是s1的邻居节点;s5位于s1的通信半径范围之外;s2对s1产生排斥作用力F12;s4对s1产生吸引作用力F14;s3和s5不对s1产生作用力;s1所受得虚拟力为F1。

图1 传感器节点的虚拟力分析Fig.1 Virtual force analysis diagram of the sensors

缺陷1。虚拟力算法通过距离阈值Dth使传感器节点间产生引力或斥力从而影响传感器节点的疏密程度和分布形式，但合适的Dth不仅与传感器节点的感知范围r有关，还受到监测区域的面积与形状的影响，不易求得。即便在最简单的矩形监测区域，虚拟力算法的最佳Dth可能由2种或3种阈值组合而成。图2为使用Dth=的无间隙等边三角形分布形式。不考虑监测区域的影响，理论上可以获得82.7% 的最佳覆盖效率［13-14］。但由于受监测区域的面积和形状的影响，完全覆盖监测区域需使用33个节点，实际覆盖效率为61.7%。若使用接近等边三角形的分布形式(见图3)，使用30个节点便可完全覆盖被监测区域，此时覆盖效率为67.9%。

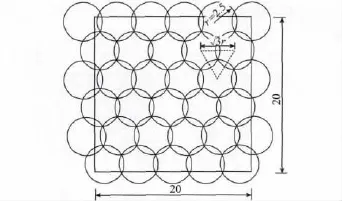
图2 理论最佳分布Fig.2 Theoretically optimal distribution

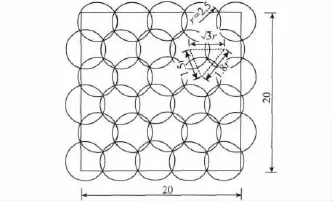
图3 实际最佳分布Fig.3 Actually optimal distribution

缺陷2。虚拟力算法中进行向量运算所得的虚拟力方向未必指向监测区域的盲区位置。如图1所示，节点s1沿虚拟力F1方向移动易与节点s3，s4产生较大的重叠覆盖区域。虚拟力算法中的增益系数wA，wR虽然可以调整虚拟力的方向和大小，但该系数的选择目前主要依靠人为经验［5，12，15］，无具体选择方法。

2.2 基于泰森多边形的部署策略

基于泰森多边形的部署算法［7-8，16］(CBS)的基本思路是先对二维监测区域进行 Voronoi图划分［17］，使每个传感器节点覆盖对应的泰森多边形以降低问题复杂度［7］，然后通过不同的方法在泰森多边形的中心区域为传感器节点寻找一个合适的位置，使传感器节点在对应泰森多边形内的覆盖率最大化。将泰森多边形形心作为传感器节点位置是较为简单直接的方法。若将n边泰森多边形n≥3的顶点坐标按顺时针方向记为(X1，Y1)，(X2，Y2)，…，(Xn，Yn)，则其形心(cx，cy)可表示为

n边形的面积M可由如下公式计算

2.3 两种算法的特点分析

VFA通过设置节点间的距离阈值Dth调整传感器节点的疏密，从而使覆盖率提升。VFA调整节点间相对位置的能力较强，在节点分布均匀性方面相比CBS有一定的优势;CBS无需设置参数，且在覆盖率上优于VFA。这两种算法的特点在文中的实验部分也将得到印证。

3 基于泰森多边形的形心导向虚拟力的部署算法

3.1 扰动向量

在Voronoi图中，可使用传感器节点判断其对应的泰森多边形顶点处是否存在盲区［18］。若泰森多边形顶点被覆盖则该顶点处不存在盲区，且节点与其邻居节点在该顶点处形成重叠覆盖，故文中设计顶点对其形心位置产生排斥作用力，使节点离开重叠覆盖区域，排斥作用力的大小为感知半径r与形心至顶点的距离之差;若泰森多边形顶点未被覆盖则该顶点处存在盲区，故文中设计顶点对其形心位置产生吸引作用力使节点向盲区移动，吸引作用力的大小为形心至顶点的距离与感知半径r之差。在此定义单个泰森多边形形心受其所有顶点的吸引作用力与排斥作用力的合力为扰动向量。

图4为一个位于泰森多边形形心处的传感器节点所对应的扰动向量。图4中当前分析节点si处于泰森多边形的形心，泰森多边形的4个顶点为v1，v2，v3，v4。顶点v1位于si的感知圆上不产生作用力，故f1=0;顶点v2和v3被si覆盖，对si分别产生排斥作用力f2，f3定义为

顶点v4未被si覆盖，对si产生吸引作用力f4，定义为

则si所受的作用力合力f'i，即该位置的扰动向量可由下式计算得出，

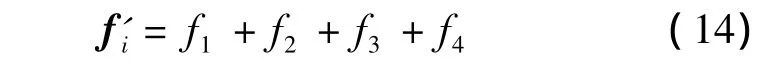
其中，r2，r3，r4分别为过顶点v2，v3，v4并以 si为终点且长度为感知圆盘半径r的向量。

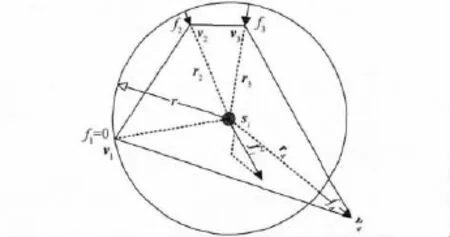
图4 扰动向量分析Fig.4 Disturbance vector analysis diagram

邻居节点为可相互通信的传感器节点且其对应的泰森多边形共边(共点)。

考虑如图1所示的5个无线传感器节点，传感器节点 si为当前分析的节点，s2，s3，s4，s5为 s1的邻居节点(s5位于s2的通信半径之内，s5可采用多跳方式通过s2与s1进行通信，故将s5定义为s1的邻居节点)。传统虚拟力算法计算s1的移动方向F1易与s3，s4产生重叠覆盖(缺陷2)。为了使s1的移动方向更加有效地指向监测区域的盲区位置，分析节点s1扰动向量的同时，考虑其所有邻居节点的扰动向量，从而使当前分析节点获得邻居节点所探测到的盲区信息和重叠覆盖区域信息，最后取有邻居关系的节点的扰动向量的均值合成虚拟力。虚拟力扰动形心分析如图 5 所示。若 s1，s2，s3，s4，s4的扰动向量分别为 f'1，f'2，f'3，f'4，f'5则 s1所受虚拟力为

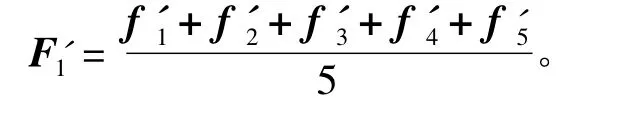
由图5中可以看出，泰森多边形形心位置C受虚拟力F'1干扰后指向的扰动位置S'1相比位置C能够更有效引导节点向监测区域的盲区扩散。

图5 虚拟力扰动形心分析Fig.5 Virtual force disturbs centroid analysis diagram

3.2 通信半径对Voronoi图划分的影响

文中使用图论中无向图连通的概念表示WSNs的连通性。若WSNs中任意两个传感器节点之间至少存在一条通信路径，则该WSNs连通;否则，此WSNs不连通。不连通的WSNs按图论中连通分量的概念划分为多个子网，每个子网在监测区域内单独进行Voronoi图划分(注:子网中传感器节点数量≥3时划分Voronoi图)。图6～图9阐述了初始化位置不连通的WSNs采用CBVFA的一次部署过程。图中的圆盘表示传感器节点的感知范围，半径为r，通信半径 Cth=2r。

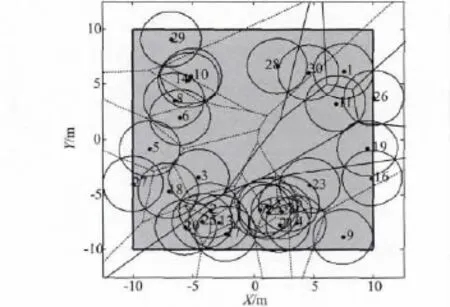
图6 传感器节点的初始化位置Fig.6 Initial position of sensors

由图6可以看出，由30个传感器节点组成的WSNs，初始化覆盖率为67.88%。初始化位置的WSNs不连通，将其划分为 A={s1，s11，s16，s19，s26，s28，s30}和 B={s2，…，s10，s12，…，s15，s17，s18，s20，…，s25，s27，s29}两个子网。A与B无法通信，故对A和B单独进行Voronoi图划分(实线为子网A的Voronoi图，虚线为子网B的Voronoi图)，并按CBVFA单独部署。在单独部署过程中，位于双方网络边缘的节点易产生过大的移动步长，如子网A中的s16和s28，子网B中的s10和s23。文中从节省能量的角度出发，设置最大移动步长［12］Maxstep=0.5r。如此经过一次迭代后WSNs连通(见图7)。

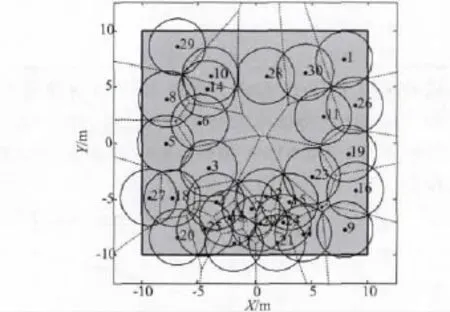
图7 第一次迭代后传感器节点位置Fig.7 Position of the sensors after Round 1

图8为部署算法迭代150次的部署移动轨迹。其中，空心圆标记为节点初始位置，实心三角标记为节点最终位置。图9为迭代完成时的节点位置，覆盖率为99.98%。

图8 传感器节点的部署轨迹Fig.8 Deployment trace of the sensors

图9 150次迭代后传感器节点的位置Fig.9 Position of the sensors after Round 150

3.3 CBVFA步骤描述

1)在监测区域T内随机部署N个传感器节点，节点的位置集合为S={s1，s2，…，sN}，si=(xi，yi)。

2)按通信半径Cth对无线传感网络连通性的影响划分子网 Subnett1，Subnett2，…，Subnetti，…。

3)在监测区域T内对子网Subnetti中的Nsub个传感器节点进行Voronoi图划分，得到泰森多边形的集合为V={v1，v2，…，vi，…，vNsub}，节点si对应的泰森多边形为vi。

5)计算所有节点位于形心处的扰动向量，扰动向量的集合为 f'={f'1，f'2，…，f'i，…，f'Nsub}。

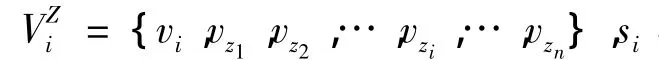
7)计算si位于形心ci处的所受得虚拟力f'i，f'i为集合f'Z中扰动向量的均值。并计算si受虚拟力f'i扰动后位置 s'i，s'i=si+f'i。计算 s'i与 si的距离 D，若D ＞Maxstep，则按sis'i方向取步长Maxstep修正s'i的位置。

8)计算节点集合{ci，z1，z2，…，zn}对的覆盖率

9)计算节点集合{s'i，z1，z2，…，zn}对的覆盖率

11)重复6)～10)，直至子网Subneti内所有节点的位置更新结束。

12)重复3)～11)，直至所有子网内的节点完成位置更新。

13)重复2)～12)，直至满足迭代停止条件。

4 仿真实验

将文献［5］中的TIVFA、文献［7］中的CBS与文献［8］中的CDVFA在覆盖率CR和节点分布均匀性U两方面与文中提出的CBVFA进行仿真实验对比。

监测区域T的大小设置为20 m×20 m，采用文献［18］中提出的方法计算完全覆盖T的理论节点数NT为30。仿真实验中各个算法采用的参数见表1。

表1 仿真实验参数Tab.1 Parameters of simulation experiment

实验1取小于NT的节点数量15在30种随机初始化位置下进行部署实验，每个实验迭代50次，得到如图10所示的部署算法在欠覆盖情况下的覆盖能力。此时，监测区域中可供节点移动的盲区大而集中。由图10可知，CBVFA的覆盖率提升较快。各部署算法的最终平均覆盖率分别为:72.67%(CBVFA)，72.46%(CDVFA)，71.19%(CBS)，61.32%(TIVFA)。

图10 15个节点数量下平均覆盖率变化曲线Fig.10 Curves of the average coverage rates under different node number

实验2取30至34个传感器节点数，每种节点数量在30种随机初始化位置下进行部署实验，每个实验迭代100次。表2为理论节点数量下取不同wA和wR在30种随机初始化位置下进行部署实验对CDVFA的最终平均覆盖率的影响。

表2 不同wA，wR对CDVFA覆盖率的影响Tab.2 Influence of different wA，wRon the coverage of CDVFA

图11比较了4种部署算法的最终平均覆盖率。表3统计了30次部署实验中各算法100%覆盖监测区域的次数。由图11和表3可知，CBVFA在覆盖率上相比其他3种部署算法具有明显优势。随着节点数量的增加只有CBVFA出现100%覆盖监测区域的情况。

图11 不同节点数量下最终覆盖率比较Fig.11 Comparison of the final coverage rates under different node number

表3 不同节点数量下30次实验得到100%覆盖率的次数Tab.3 Times of getting 100% coverage rate in 30 experiments under different node number

图12比较了在不同节点数量下，4种部署算法在30次部署实验中的节点分布均匀性的均值。

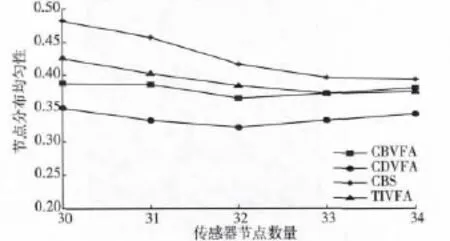
图12 不同节点数量下节点分布均匀性比较Fig.12 Distribation uniformity ofsensors under different node number

由图12可以看出，CDVFA的节点分布均匀性最好，CBVFA次之。

5 结语

文中提出的CBVFA利用泰森多边形顶点对传感器节点产生虚拟力，避免了传统虚拟力算法需要设置距离阈值Dth和权重参数wR，wA的缺陷，并在CBS中加入邻居节点的影响，与传统的虚拟力算法和CBS相比较，文中所提的部署算法具有较好的性能。

［1］毛晓峰，杨珉，毛迪林.无线传感器网络应用综述［J］.计算机应用与软件，2008，25(3):179-181.

MAO Xiaofeng，YANG Min，MAO Dilin.Research on sensor technology face to wireless sensor network［J］.Computer Applications and Software，2008，25(3):179-181.(in Chinese)

［2］任彦，张思东，张宏科.无线传感器网络中覆盖控制理论与算法［J］.软件学报，2006，17(3):422-433.

REN Yan，ZHANG Sidong，ZHANG Hongke.Theories and algorithms of coverage control for wireless sensor networks［J］.Journal of Software，2006，17(3):422-433.(in Chinese)

［3］Howard A，Mataric M J，Sukhatme G S.An incremental self-deployment algorithm for mobile sensor networks［J］.Autonomous Robots，2002，13(2):113-126.

［4］Howard A，Mataric M J，Sukhatme G S.Mobile Sensor Network Deployment Using Potential Fields:A Distributed，Scalable Solution to the Area Coverage Problem［M］.Tokyo:Springer Japan，2002:299-308.

［5］LI S，XU C，PAN W，et al.Sensor deployment optimization for detecting maneuvering targets［C］//Proceedings of the 2005 8th International Conference on Information Fusion.Piscataway，NJ:IEEE，2005:1629-1635.

［6］YU X，HUANG W，LAN J，et al.A novel virtual force approach for node deployment in wireless sensor network［C］//Proceedings of the 2012 IEEE 8th International Conference on Distributed Computing in Sensor Systems.Piscataway，NJ:IEEE，2012:359-363.

［7］LEE H J，KIM Y H，HAN Y H，et al.Centroid-based movement assisted sensor deployment schemes in wireless sensor networks［C］//Proceedings of the 2009 IEEE 70th Vehicular Technology Conference Fall.Piscataway，NJ:IEEE，2009:1-5.

［8］HAN Y H，KIM Y H，KIM W，et al.An energy-efficient self-deployment with the centroid-directed virtual force in mobile sensor networks［J］.Simulation，2011，88(10):1152-1165.

［9］张骞，李克清，戴欢，等.基于协同进化蜂群算法的覆盖优化策略［J］.计算机工程与设计，2014，25(4):1142-1146.

ZHANG Qian，LI Keqing，DAI Huan，et al.Coverage optimization strategy based on co-evolution bee colony algorithm［J］.Computer Engineering and Design，2014，25(4):1142-1146.(in Chinese)

［10］熊伟丽，刘欣，陈敏芳，等.基于差分蜂群算法的无线传感器网络节点分布优化［J］.控制工程，2014，21(6):1036-1040.

XIONG Weili，LIU Xin，CHEN Minfang，et al.Node distribution optimization in wireless sensor networks based on differential bee colony algorithm［J］.Control Engineering of China，2014，21(6):1036-1040.(in Chinese)

［11］刘丽萍.无线传感器网络节能覆盖［D］.杭州:浙江大学，2006.

［12］王雪，王晟，马俊杰.无线传感网络布局的虚拟力导向微粒群优化策略［J］.电子学报，2007，35(11):2038-2042.

WANG Xue，WANG Sheng，MA Junjie.Dynamic sensor deployment strategy based on virtual force-directed particle swarm optimization in wireless sensor networks［J］.Acta Electronica Sinica，2007，35(11):2038-2042.(in Chinese)

［13］关志艳，耿岩.虚拟力导向群聚智能优化的无线传感器网络覆盖策略［J］.传感器与微系统，2015，34(1):40-42，46.

GUAN Zhiyan，CENG Yan.Coverage strategy for wireless sensor networks based on virtual force directed swarm intelligence optimization［J］.Transducer and Microsystem Technologies，2015，34(1):40-42，46.(in Chinese)

［14］杨云，石婷婷，徐平，等.一种具有鲁棒性的异构传感器网络部署策略［J］.计算机应用与软件，2011(6):51-53，68.

YANG Yun，SHI Tingting，XU Ping，et al.A new deployment strategy for heterogeneous wireless sensor networks with robustness［J］.Computer Applications and Software，2011(6):51-53，68.(in Chinese)

［15］WANG Y C，WU F J，TSENG Y C.Mobility management algorithms and applications for mobile sensor networks［J］.Wireless Communications and Mobile Computing，2012，12(1):7-21.

［16］Mahboubi H，Moezzi K，Aghdam A G，et al.Distributed deployment algorithms for improved coverage in a network of wireless mobilesensors［J］.IEEE Transactions on Industrial Informatics，2014，10(1):163-174.

［17］赵春江，吴华瑞，刘强，等.基于Voronoi的无线传感器网络覆盖控制优化策略［J］.通信学报，2013(9):115-122.

ZHAO Chunjiang，WU Huarui，LIU Qiang，et al.Optimization strategy on coverage control in wireless sensor network based on Voronoi［J］.Journal on Communications，2013(9):115-122.(in Chinese)

［18］方伟，宋鑫宏.基于Voronoi图盲区的无线传感器网络覆盖控制部署策略［J］.物理学报，2014，63(22):132-141.

FANG Wei，SONG Xinhong.A deployment strategy for coverage control in wireless sensor networks based on the blind-zone of Voronoi diagram［J］.Acta Phys Sin，2014，63(22):132-141.(in Chinese)