考虑光伏和负荷相关性的概率潮流计算

任洲洋　颜　伟　项　波　赵　霞　王强钢　余　娟

（1. 输配电装备及系统安全与新技术国家重点实验室（重庆大学）　重庆　400044

2. 国网重庆市电力公司万州供电分公司　重庆　404160）

考虑光伏和负荷相关性的概率潮流计算

任洲洋1颜伟1项波2赵霞1王强钢1余娟1

（1. 输配电装备及系统安全与新技术国家重点实验室（重庆大学）重庆400044

2. 国网重庆市电力公司万州供电分公司重庆404160）

位于相邻地区的光伏电源输出功率和负荷之间存在较强的相关关系，而现有的概率潮流研究并未准确计及。通过结合参数和非参数概率建模理论，提出了一种光伏功率的综合建模方法，该方法能够准确反映光伏功率的随机特性且无需任何参数分布的假设信息。利用等概率转换原则和Cholesky分解技术处理多个光伏电源的输出功率之间及其与负荷之间的相关关系。在此基础上，进一步提出了一种能够准确计及任意分布的光伏和负荷相关性的Monte Carlo概率潮流计算方法，并引入中值拉丁超立方抽样技术以提高抽样效率，降低计算复杂度。针对美国某光伏电站的实测数据和69节点配电系统进行仿真分析，验证了所提方法的准确性和有效性。

光伏发电相关性蒙特卡洛概率潮流

0　引言

太阳能光伏发电具有绿色、环保和无污染等优点，近年来得到了持续快速发展，截至2012年底，全球总装机容量已达100GW[1]。但不容忽视，光伏发电属于典型的间歇式能源，其输出功率严重依赖于辐照、温度等气象条件，具有较强的随机波动性。无疑，光伏的大规模接入将进一步加剧电力系统的不确定性。而概率潮流作为电力系统不确定性分析的重要工具，其能够充分考虑系统中的随机因素，为电力系统的经济运行、可靠性及安全稳定分析等提供全面、重要的参考信息，因而近年来被广泛用于含光伏等随机因素的系统分析中[2-7]。可见，有必要对含光伏电力系统的概率计算方法展开深入研究。

国内外的电力学者在该领域进行了大量的研究工作。文献[8]采用Beta分布建立光伏功率的概率模型，并基于半不变量法与Gram-Charlier级数展开技术计算系统各节点电压的概率分布。文献[9,10]利用直接辐照和散射辐照的概率密度函数获取光伏功率的概率分布，同样结合半不变量和Gram-Charlier级数展开技术求解概率潮流。文献[11,12]基于晴朗指数的概率分布[13]及其与光伏功率的函数关系建立了后者的概率模型，并采用Monte Carlo模拟技术进行概率潮流分析。上述文献基于概率潮流深入分析了光伏功率随机性对电力系统运行的影响，但未涉及光伏功率之间及与负荷之间的相关关系。然而实际上，对位于相邻地区的多个光伏电源以及气象条件敏感负荷（如空调负荷等）而言，其处于类似的气象条件下，相互之间存在一定的相关关系，因此，需在概率潮流分析中充分考虑上述相关关系。

文献[14]基于半不变量法提出了能够考虑多个光伏电源输出功率相关性的概率潮流计算方法，但存在以下问题：

（1）该方法所采用的光伏Beta模型适应性差，极有可能引入较大误差。作者前期的研究表明光伏电源的输出功率并不总是服从Beta、正态等常规参数分布[15]。

（2）对不服从Beta分布或无法用常规参数分布建模的光伏而言，如何处理其相互之间以及与负荷之间的相关关系，文献[14]并未考虑。

（3）该方法涉及到自半不变量和联合半不变量的求解，其计算规模随输入变量数和阶数的增加而急剧增长，计算量过大。现有研究也常基于等概率转换原则处理服从参数分布的风电相关性[2,16]，但对于无法采用参数分布建模的情况，尚无文献讨论。因此，无法将该方法直接用于考虑光伏、负荷相关性的概率潮流分析中。

本文基于Monte Carlo模拟技术提出了一种能够准确计及任意分布的光伏功率和负荷相关性的概率潮流计算方法：结合参数和非参数概率建模理论，提出一种光伏电源输出功率的综合建模方法；利用等概率转换原则和Cholesky分解技术处理光伏功率之间及其与负荷之间的相关关系；基于Monte Carlo模拟和中值拉丁超立方抽样技术实现概率潮流的快速求解。

1　光伏电源输出功率的综合概率建模方法

基于Beta分布的光伏概率模型具有简单、易实现等优点，并且对实测数据样本的要求不高，但该模型并不具有普遍适用性，即采用光伏的Beta模型并不一定总能够取得良好的模拟效果。光伏的非参数核密度估计模型虽然具有较强的适应性和较高的模拟准确度，但是该模型的表达式复杂，计算量相对较大，而且对实测数据样本有着较高的要求。为了综合利用上述两种建模方法的优点，本文提出了一种光伏功率的综合概率建模方法。该方法不仅能够准确模拟具有任意随机分布特性的光伏功率，还具有较强的适应性和更宽的适用范围，同时兼顾了光伏的Beta模型和非参数核密度估计模型的优点。光伏综合概率建模方法的流程图和实现步骤如图1所示。

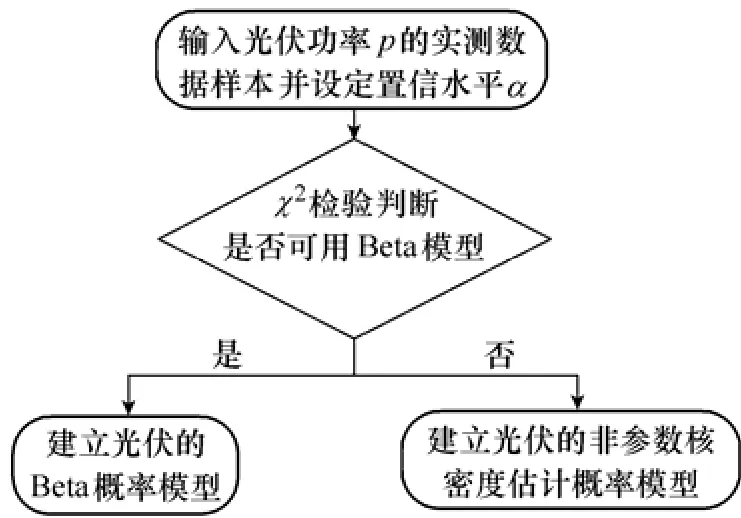
图1　光伏综合概率建模方法的流程Fig.1　The flowchart of the comprehensive probabilisticmodeling method of photovoltaic generation

（1）基于χ2检验方法判断是否可采用Beta分布。输入光伏电源输出功率p的实测数据样本pv1, pv2,…, pvn，基于χ2检验方法[17]，判断是否可用Beta分布描述p的概率分布，若可以，则根据下面的步骤（2）建立光伏的Beta概率模型；否则，根据下面的步骤（3）建立光伏的非参数核密度估计模型。

（2）基于Beta分布的光伏概率模型。根据Beta分布可估计光伏功率p的概率密度函数f (p)为[18]

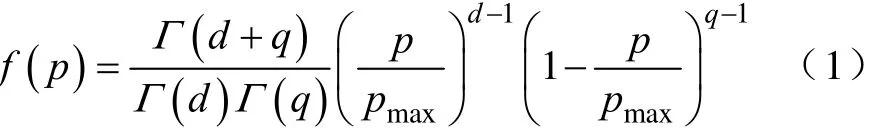
式中，pmax为光伏功率的最大值；Г(*)为Gamma函数；d、q均为Beta分布的形状参数。

（3）基于非参数核密度估计的光伏概率模型。基于非参数核密度估计理论，可近似估计f(p)为[15]

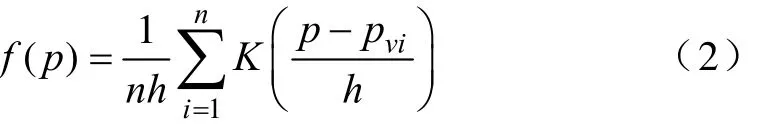
式中，n为光伏实测数据的样本数；h为带宽，可由经验算法计算得到[19]；K(·)为核函数，本文选择常见的高斯函数作为核函数[19]。

2　考虑光伏负荷相关性的随机抽样方法

对于存在相关关系的光伏功率和负荷而言，其随机样本无法直接抽样产生。为此，本文首先产生相互独立的标准正态随机样本，然后，基于等概率转换原则和Cholesky分解技术将其转换为存在相关关系的光伏功率、负荷随机样本。转换共分为两步：①将相互独立的标准正态随机样本转换为相关的标准正态随机样本；②将相关的标准正态随机样本转换为服从指定分布、具有给定相关系数的光伏、负荷随机样本。具体原理及抽样步骤如下。

2.1基于等概率转换原则的非标准正态分布转换

假设系统中共有m个相关的随机变量p1, p2,…, pm，并将之表示为向量P=(p1, p2,…, pm)。其中，p1, p2,…, pa分别表示a个光伏电源的输出功率，均服从Beta分布；pa+1, pa+2,…, pa+b分别表示b个光伏电源的输出功率，其概率模型均为非参数核密度估计模型；pa+b+1, pa+b+2,…, pa+b+c分别表示c个服从正态分布的负荷。ρij为变量pi与pj间的相关系数；f(pi)、F(pi)分别为变量pi的概率密度函数和累积概率密度函数，其中，i=1, 2,…, m。根据下式所示的等概率转换原则[20]可将向量P转换为标准正态随机向量Y= (y1, y2,…, ym)，其中yi与yj间的相关系数为ρyij(i, j=1, 2,…, m)。

式中，Φ (yi)为yi的标准正态累积分布函数；Fi-1为累积分布函数F的反函数。

根据上式及相关系数的定义[21]，可得到ρij和ρyij之间的函数关系为

式中，φyij表示标准二元正态分布的概率密度函数，φyij的相关系数参数为ρyij。采用二分法即可求解得到ρyij，详细求解步骤参见文献[22]。

根据式（5），可以得到Y的协方差矩阵Cy为

2.2基于Cholesky分解的相关标准正态分布转换

接下来需要将Y进一步转换为相互独立的标准正态随机向量H，具体原理及步骤如下。

存在下三角矩阵L将Y= (y1, y2,…, ym) 转换为相互独立的标准正态随机向量H= (h1, h2,…, hm)

式中，L可通过对Y的协方差矩阵Cy进行Cholesky分解得到[2]

2.3光伏负荷相关随机样本的抽样步骤

2.1和2.2节介绍了如何将光伏、负荷等相关随机向量P转换为相互独立的标准正态随机向量H，那么，根据其逆过程即可由独立的标准正态随机样本产生光伏、负荷的相关随机样本。另外，为进一步提高抽样效率，本文还引入了中值拉丁超立方抽样技术[23]以实现对标准正态随机样本的抽样。综上所述，光伏、负荷相关随机样本的抽样步骤如下所示：

（1）读入光伏、负荷的概率模型信息（分布类型及参数）、存在相关关系的变量数m和相关系数ρij（i, j= 1, 2,…, m），并设定采样规模s。

（2）根据式（4）、式（5）由ρij（i, j= 1, 2,…, m）计算得到Y的协方差矩阵Cy，并对Cy进行Cholesky分解，得到下三角矩阵L。

（3）基于中值拉丁超立方抽样技术产生m×s维的标准正态随机样本矩阵H。

（4）根据Y=LH求取矩阵Y，此时Y的协方差矩阵即为Cy。

（5）根据式（3）依次转换Y中各元素，得到P，此时P即为光伏和负荷的相关随机样本。

3　基于Monte Carlo模拟的概率潮流计算方法

结合第2节提出的相关随机样本抽样方法，采用Monte Carlo模拟技术求解含光伏电力系统的概率潮流，具体计算步骤如下：

（1）输入网络结构参数、光伏和负荷的概率模型信息（分布类型、参数）及相关系数，并设定中值拉丁超立方采样规模s。

（2）根据2.3节中的步骤（1）～步骤（5）产生存在相关关系的光伏、负荷随机样本。

（3）对相互独立的光伏、负荷随机变量，直接采用中值拉丁超立方技术产生随机样本。

（4）采用牛顿-拉夫逊法依次进行s次确定性的潮流计算。

（5）统计节点电压、线路传输功率及线损率等指标的样本信息，并利用非参数核密度估计理论绘制各指标的概率密度曲线。

4　算例分析

4.1测试网络及数据

采用69节点配电系统[24]，进行仿真分析，该系统共有负荷3 802.19+j2 694.6kV·A，网络接线图如下所示，其中，编号带下划线的节点为负荷节点。

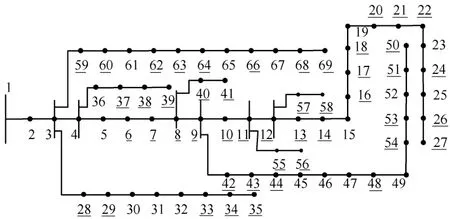
图2　69节点配电系统Fig.2　The 69-node distribution network

假设系统共接入三个光伏电源P1、P2和P3，其中P1额定容量为200kW，服从形状参数为2.06和2.50的Beta分布；P2额定容量为400kW，服从形状参数为2.12和2.80的Beta分布；P3额定容量为200kW，输出功率样本为美国某光伏电站的实测数据[25]，经χ2检验知，光伏功率的随机变化不服从Beta分布，故建立P3的非参数核密度估计模型。将P1、P2和P3依次接在节点39、50和53处，并假设P1、P2和P3之间及其与节点11、12和38上的有功负荷L11、L12和L38之间存在关联关系，相关系数均为0.5。另外，假设所有的负荷都服从正态分布，均值为节点负荷的稳态值，标准差为均值的5%。

4.2所提概率潮流计算方法的验证

针对69节点配电系统，基于本文方法进行概率潮流分析，其中，中值拉丁超立方的采样规模为500次。同时，利用直接抽样法进行采样规模为3万次的Monte Carlo概率潮流计算，并认为该方法所得计算结果是准确无误的，可作为验证本文方法的标准。

表1所示为两种方法计算所得节点50的电压均值σv、标准差μv；线路38、39视在功率的均值μt、标准差σt；系统线损的均值μl、标准差σl。可知，两种方法所得结果基本一致，即本文所提出概率潮流计算方法能够准确获取电压、线路传输功率和线损的概率统计信息，具有较高的计算准确度。另外，与直接抽样法相比，本文方法具有较高的抽样效率，计算复杂度降低。

表1　69节点系统的概率潮流计算结果Tab.1　The probabilistic power flow results of 69-node distribution network

4.3光伏负荷相关性对配网运行的影响分析

为分析光伏和负荷相关性对配网运行的影响，将P1、P2、P3、L11、L12、L38之间相关系数分别设定为0、0.3、0.6和0.9，并采用本文方法依次计算概率潮流。

不同相关系数情况下，系统各节点电压的均值和标准差变化曲线如图3、图4所示。图5为节点50电压的概率密度曲线。由图3、图4可知，光伏和负荷之间的相关程度对各节点电压的均值影响极小，但对节点电压的标准差影响较大，尤其是光伏接入节点及其附近节点，这也意味着光伏负荷相关程度的增强将会进一步加剧节点电压的波动性。这是因为随着光伏负荷相关程度的提高，其功率变化的同步性逐步增强，从而节点电压的波动性也随之增加。由图5可知，在不同的相关系数情况下，节点电压的概率分布是有差别的，但未呈现出规律的变化趋势。

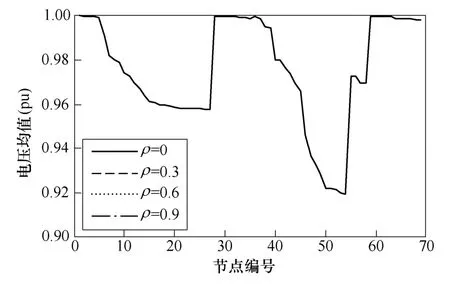
图3　节点电压的均值Fig.3　The mean values of bus voltage magnitudes

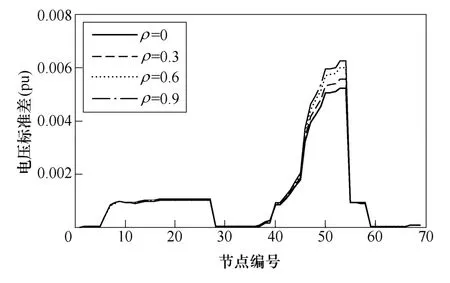
图4　节点电压的标准差Fig.4　The standard deviation values of bus voltage magnitudes

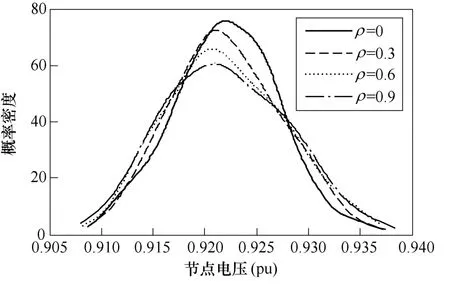
图5　节点50电压的概率密度曲线Fig.5　The probability density curves of voltage magnitude at bus 50

不同相关系数情况下，各线路视在功率的均值及标准差变化曲线如图6和图7所示。线路50，51视在功率的概率密度曲线如图8所示。可见，线路视在功率的均值基本不受光伏、负荷相关水平的影响，但不同相关系数下，线路视在功率的标准差则相差较大，尤其是光伏接入点以及根节点附近的支路。原因在于，随着相关系数的增加，光伏和负荷功率变化的同步性增强，相应的，线路传输功率的波动性也逐步增强。从图8可知，线路传输功率的概率分布同样受到光伏和负荷相关程度的影响，但是随着相关程度的增强，线路传输功率概率分布的变化并未呈现出一定的规律性。

图6　线路视在功率的均值Fig.6　The mean values of line flows

图7　线路视在功率的标准差Fig.7　The standard deviation values of line flows

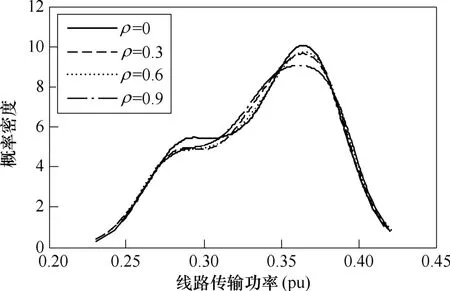
图8　线路50和51视在功率的概率密度曲线Fig.8　The probability density curves of the line flow through bus 50 and 51

不同相关系数情况下，69节点配电系统的线损率均值和标准差见表2。线损率的概率密度曲线如图9所示。不难看出，随着相关程度的增强，线损率的均值基本没有变化，但标准差却逐渐增大。而线损率的概率分布同样会受到光伏、负荷相关程度的影响，因此，低估或忽略光伏和负荷之间的相关关系将无法准确获取线损率的概率分布信息。

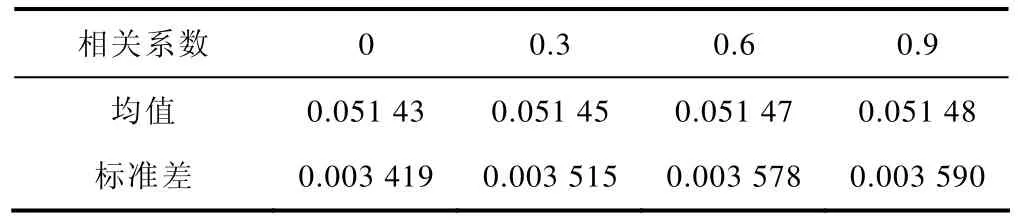
表2　线损率的均值和标准差Tab.2　The mean and standard deviation values of network loss rate

图9　线损率的概率密度曲线Fig.9　The probability density curves of network loss rate

5　结论

本文提出了一种能够准确计及任意分布的光伏功率和负荷相关性的Monte Carlo概率潮流计算方法，并采用69节点配电系统进行仿真分析，验证了本文方法的准确性和有效性。研究表明：

（1）光伏、负荷之间的相关关系对节点电压、线路传输功率及线损率等指标的均值影响不大，但是会对上述指标的标准差及概率分布产生较大影响。

（2）随光伏、负荷相关程度的增强，节点电压、线路传输功率和线损率等指标的波动性将会进一步增强，另外，上述指标的概率分布同样受光伏、负荷相关水平的影响。

（3）忽略或错误估计光伏、负荷之间的相关关系将无法得到准确的概率潮流分析结果。

[1] Arthouros Zervos. Renewables 2013 global status report. renewable energy policy network for the 21st century[M]. Paris, France, 2013.

[2] Chen Yan, Wen Jinyu, Cheng Shijie. Probabilistic load flow method based on nataf transformation and latin hypercube sampling[J]. IEEE Transactions on Sustainable Energy, 2013, 4(2): 394-301.

[3] 董雷, 杨以涵, 张传成, 等. 综合考虑网络结构不确定性的概率潮流计算方法[J]. 电工技术学报, 2012, 27(1): 210-216.

Dong lei, Yang Yihan, Zhang Chuancheng, et al. Probabilistic load flow considering network configuration uncertainties[J]. Transactions of China Electrotechnical Society, 2012, 27(1): 210-216.

[4] 洪芦诚, 石立宝, 姚良忠, 等. 计及风电场发电功率不确定性的电力系统模糊潮流[J]. 电工技术学报, 2010, 25(8): 116-122.

Hong Lucheng, Shi Libao, Yao Liangzhong, et al. Fuzzy modelling and solution of load flow incorporating uncertainties of wind farm generation［J］. Transactions of China Electrotechnical Society，2010，25（8）： 116-122.

[5] 张谦, 奚巍民, 黄俊辉, 等. 考虑系统运行方式的江苏电网过江断面概率潮流实证分析[J]. 电力系统保护与控制, 2013, 41(1): 47-52.

Zhang Qian, Xi Weimin, Huang Junhui, et al. Probabilistic load flow evaluation considering system operation mode for transmission lines across the Yangzi river of Jiangsu power grid[J]. Power Systems Protection and Control, 2013, 41(1): 47-52.

[6] 文旭, 颜伟, 黄淼, 等. 计及绿色能源出力不确定性的输电网线损率概率评估[J]. 电力系统保护与控制, 2013, 41(1): 169-175.

Wen Xu, Yan Wei, Huang Miao, et al. Probabilistic transmission loss rate evaluation under green energy generation uncertainty[J]. Power Systems Protection and Control, 2013, 41(1): 169-175.

[7] 刘志刚, 刘欢, 柳杰. 计及风电场概率模型的多目标无功优化[J]. 电力系统保护与控制, 2013, 41(1): 197-203.

Liu Zhigang, Liu Huan, Liu Jie. Multi-objective reactive power optimization considering wind farm probabilistic model[J]. Power Systems Protection and Control, 2013, 41(1): 197-203.

[8] 王成山, 郑海峰, 谢莹华, 等. 计及分布式发电的配电系统随机潮流计算[J]. 电力系统自动化, 2005, 29(24): 39-44.

Wang Chengshan, Zheng Haifeng, Xie Yinghua, et al. Probabilistic power flow containing distribution generation in distribution system[J]. Automation of Electric Power Systems, 2005, 29(24): 39-44.

[9] Ruiz-Rodriguez F J, Hernandez J C, Jurado F. Probabilistic load flow for photovoltaic distributed generation using the cornish-fisher expansion[J].Electric Power Systems Research, 2012, 89(1): 129-138.

[10] Ruiz-Rodriguez F J, Hernandez J C, Jurado F. Probabilistic load flow for radial distribution networks with photovoltaic generators［J］. IET Renewable Power Generation, 2012, 6(2): 110-121.

[11] 段玉兵, 龚宇雷, 谭兴国, 等. 基于蒙特卡罗模拟的微电网随机潮流计算方法[J]. 电工技术学报, 2011, 26(增刊1): 274-278.

Duan Yubing, Gong Yulei, Tan Xingguo, et al. Probabilistic power flow calculation in microgrid based on monte-carlo simulation[J]. Transactions of China Electrotechnical Society, 2011, 26(S1): 274-278.

[12] Conti S, Raiti S. Probabilistic load flow using Monte Carlo techniques for distribution networks with photovoltaic generators[J]. Solar Energy, 2007, 81(12): 1473-1481.

[13] Hollands K G T, Huget R G. A probability density function for the clearness index with applications[J], Solar Energy, 1983, 30(3): 195-209.

[14] Miao F, Vijay V, Gerald T H, et al. Probabilistic power flow studies for transmission systems with photovoltaic generation using cumulants[J]. IEEE Transactions on Power Systems, 2012, 27(4): 2251-2261.

[15] 颜伟, 任洲洋, 赵霞, 等. 光伏电源输出功率的非参数核密度估计模型[J]. 电力系统自动化, 2013, 37(10): 35-40.

Yan Wei，Ren Zhouyang，Zhao Xia，et al. Probabilistic photovoltaic power modeling based on nonparametric kernel density estimation[J]. Automation of Electric Power Systems, 2013, 37(10): 35-40.

[16] 蔡德福，陈金福，石东源，等. 风速相关性对配电网运行特性的影响［J］. 电网技术，2013，37（1）： 150-155.

Cai Defu, Chen Jinfu, Shi Dongyuan, et al. Impact of wind speed correlation on operation characteristics of distribution network[J]. Power System Technology, 2013, 37(1): 150-155.

[17] 杨虎, 刘琼荪, 钟波. 数理统计[M]. 北京: 高等教育出版社, 2004.

[18] Karaki S H, Chedid R B, Ramadan R. Probabilistic performance assessment of autonomous solar-wind energy conversion systems[J]. IEEE Transactions on Energy Conversion, 1999, 14(3): 766-772.

[19] 赵渊, 沈智健, 周念成, 等. 基于序贯仿真和非参数核密度估计的大电网可靠性评估[J]. 电力系统自动化, 2008, 32(6): 14-19.

Zhao Yuan, Shen Zhijian, Zhou Niancheng, et al. Reliability assessment of bulk power systems utilizing sequential simulation and nonparametric Kernel density estimation[J]. Automation of Electric Power Systems, 2008, 32(6): 14-19.

[20] Liu P L, Der Kiureghian A. Multivariate distribution models with prescribed marginals and covariances[J]. Probabilistic Engineering Mechanics, 1986, 1(2): 105-112.

[21] 盛骤, 谢式千, 潘承毅. 概率论和数理统计[M]. 北京: 高等教育出版社, 2001.

[22] Qin Zhilong, Li Wenyuan, Xiong Xiaofu. Generation system reliability evaluation incorporating correlations of wind speeds with different distributions[J]. IEEE Transactions on Power Systems, 2013, 28(1): 551-558.

[23] Yu H, Chung C Y, Wong K P, et al. Probabilistic load flow evaluation with hybrid latin hypercube sampling and Cholesky decomposition[J]. IEEE Transactions on Power Systems, 2009, 24(2): 661- 667.

[24] Baran M E, Wu F. Optimal capacitor placement on radial distribution systems[J]. IEEE Transactions on Power Delivery, 1989, 4(1): 725-734.

[25] 光伏电站小时输出功率数据. 网址: http://solardata. uoregon. edu/SelectArchival.html.

Probabilistic Power Flow Analysis Incorporating the Correlations between PV Power Outputs and Loads

Ren Zhouyang1Yan Wei1Xiang Bo2Zhao Xia1Wang Qianggang1Yu Juan1
（1. State Key Laboratory of Power Transmission Equipment & System Security and New Technology Chongqing UniversityChongqing400044China
2. Wanzhou Power Supply Company of State Grid Chongqing Electric Power Corporation Chongqing404160China）

The correlations between power outputs of photovoltaic (PV) generators and loads at adjacent locations actually exist and are not accurately considered in the current research on the probabilistic power flow analysis. Based on the parametric and nonparametric probabilistic modeling theories, the comprehensive model of PV generation is proposed and the randomness of PV outputs can be accurately reflected without any assumption of theoretical distributions. The correlations between the PV outputs and loads are considered by combining the marginal transformation and Cholesky decomposition techniques. Furthermore, the Monte Carlo based probabilistic power flow analysis method is developed, which can capture the correlations between PV outputs and loads obeying different probability distributions. The Latin Hypercube Sampling method, an efficient sampling method, is also introduced to decrease the computation burden. The measured power data of PV generator in USA and the 69-node distribution network are used to demonstrate the correctness and effectiveness of the presented probabilistic power flow analysis method.

Photovoltaic generation, correlation, Monte Carlo, probabilistic power flow

TM744

任洲洋男，1986年生，博士，讲师，研究方向为电力系统风险评估和电力系统大数据分析。

颜伟男，1968年生，博士，教授，博士生导师，研究方向为电力系统规划与优化运行和电力系统风险评估。

中央高校基本科研业务费资助项目（106112015CDJXY 150002）。

2013-12-12改稿日期 2014-04-14