静止式中频电源组网系统模式切换暂态过程控制

朱俊杰　 聂子玲　马伟明

（海军工程大学舰船综合电力技术国防科技重点实验室　武汉　430033）

静止式中频电源组网系统模式切换暂态过程控制

朱俊杰 聂子玲马伟明

（海军工程大学舰船综合电力技术国防科技重点实验室武汉430033）

静止式中频电源组网系统模式切换暂态控制对于整个系统的稳定运行有着至关重要的作用。为此，分析了静止式中频电源组网过程中带与不带本地负载时组网、独立运行的原理，并以此为基础，深入研究开关顺序对组网系统模式切换暂态过程的影响，得出组网时模式开关先闭合、脱网时静态开关先分断为最优开关顺序的结论；同时，为了保证组网单元在组网和脱网过程中以较小的电流冲击实现模式切换的平稳过渡，提出一种静止式中频电源组网系统模式切换平滑控制策略，即通过电流峰值的平均分配及峰值、相位的平滑调节，实现从机单元的无冲击并网，并给出具体实施步骤。仿真和实验结果证明了模式切换暂态过程理论分析的正确性及平滑控制的有效性。

静止式中频电源组网系统模式切换开关顺序暂态过程平滑控制

0　引言

静止式中频电源多用于航空和军事领域，目前，随着军事和经济的发展，上述领域对于中频供电系统的容量需求越来越大，而静止式中频电源的组网运行可以灵活地扩大系统容量，方便地组成冗余系统，提高运行的可靠性［1-3］。

然而，对于静止式中频电源组网系统而言，模式切换暂态过程控制的好坏对组网系统的稳定性和组网各单元设备的寿命有着至关重要的作用。组网单元与中频电网之间的无缝切换，可以保证组网单元内重要负荷的供电连续性，对电网的安全稳定运行也具有重要的作用，已经作为组网系统的重要技术特征引起了广泛的重视［4，5］。

目前，对于模式切换研究较多的集中在工频领域，主要表现为单台工频逆变器或微电网带本地负载时，与大电网之间的脱/并网切换过程［6-9］。文献［10］提出了一种基于储能的微网并网/离网无缝切换技术，该技术利用储能可以在电压控制模式和电流控制模式间灵活快速转换，完成电源组网和脱网的角色转换，但该方法不能直接适用于高度弱阻尼的静止式中频电源，且增加了储能单元。文献［11］提出了一种基于逻辑芯片UTC4053的硬件电路切换方法来实现逆变系统并网和独立两种工作模式的切换。该方法将并网运行控制方法和独立运行控制方法作为两个输入通道，然后由单片机给定模式选择信号并经UTC4053实现通道的选择，即并/脱网状态，这对于小功率、简单的工频逆变器效果较好，而大容量静止式中频电源系统输出电流较大，且通道切换产生的延时对于相位同步控制影响加大，可靠性降低。文献［12］研究了单独逆变器带本地负载时并/脱网控制，并结合逆变器自身控制方法，给出了模式切换算法，但缺乏对于模式切换暂态过程的详细分析。上述研究均是基于工频系统，然而，中频系统均流控制和相位同步控制的难度更大。对于中频系统而言，输出电压频率是工频的8倍，当采样频率为10kHz时，对于工频系统，一个基波周期内采样200次，而中频系统一个基波周期内仅能采样25次，通过采样得到的电压、电流数据计算的有功、无功准确度远不如工频逆变器［13］。当开关频率为10kHz时，对于工频系统，开关器件两次动作之间的相位差为1.8°，而中频系统开关器件两次动作之间相位差为14.4°，组网系统模式切换控制的难度大大增加。

本文通过静止式中频电源组网系统模式切换暂态分析，得出最优开关顺序，即组网时模式开关（Mode Switch，MS）先闭合、脱网时静态开关（Solid-State Switch，SSS）先分断；同时，提出一种组网系统模式切换平滑控制策略，减小系统环流，并通过仿真和实验予以验证。

1　组网系统运行模式原理

为了分析组网系统运行模式原理，首先给出静止式中频电源拓扑结构，如图1所示。静止式中频电源采用双H桥级联的组合式三相四线制逆变器拓扑结构，各相可独立控制。以A相为例，两个400Hz H桥型逆变器经相同输出变压器的次级串联在一起，单个逆变器内部同时采用倍频PWM控制方法，H桥型逆变器之间采用交错控制技术，即载波移相控制，两个H桥的左右桥臂输出端电压均可由载波PWM实现，从而增加了控制的自由度。根据多电平载波移相方法的思想，对于一个五电平变换器，四个互错90°的三角载波分别与调制波进行比较，生成相对独立的四组两两互反的PWM调制信号，去驱动八个功率单元，每一个H桥单元退化为两电平的PWM控制，两个H桥的输出相加生成一个等效五电平PWM波形，从而提高系统的控制带宽，有效地保证了输出电压的波形质量。

图1　三相四线制静止式中频电源主电路拓扑结构Fig.1　The main circuit topology of three-phase four-wire solid-state power supply

静止式中频电源组网系统模式切换暂态过程与其采用的工作模式息息相关，为了更好地分析和控制组网系统暂态过程，必须对采用不同工作模式的系统加以区别分析。

1.1组网过程中不带本地负载

当静止式中频电源组网过程中不带本地负载时，其工作原理如图2所示。图中RUN为PWM脉冲输出指令，此时，静止式中频电源组网系统只要求组网电源工作在组网工作模式，控制相对简单。并网时，首先由组网单元内部控制器发出指令闭合静态开关SSS，然后将脉冲输出指令RUN置1实现电源的并网。脱网时，首先将脉冲输出指令RUN置0封锁组网单元脉冲，然后由内部控制器发出指令打开SSS开关，组网单元脱网停机。静止式中频电源组网过程中不带本地负载模式下，组网单元的独立运行并没有参与到并/脱网过程中，其开关顺序相对固定，不存在电源独立工作模式，因此，对于组网单元本身来讲，内部工作模式单一，其并/脱网的暂态过程（主要为环流大小）完全取决于组网控制策略的性能。

图2　静止式中频电源组网过程中不带本地负载模式原理Fig.2　Principle of integration of 400Hz solid-state power supply without local load

1.2组网过程中带本地负载

当静止式中频电源组网过程中带本地负载时，组网单元需根据指令分别工作在并网运行和独立运行两种工作模式，且能实现两种工作模式的平滑切换。图3为静止式中频电源带本地负载模式下组网、独立运行原理结构。图中MS表示模式开关，组网电源输出电压和电流分别为UO和IO，馈入电网电流为Ig，本地负载端电压和电流分别为UL和IL。组网单元在独立模式时采用电压、电流双闭环控制即电压源输出模式，在组网模式时采用单电流环控制即电流源输出模式，组网单元输出端与电网的连接通过SSS控制，SSS闭合为组网单元输出端接入电网，SSS断开为组网单元脱离电网。上位机通过MS逻辑控制组网单元在双闭环输出控制模式和电流环控制模式之间的切换。文中组网单元各工作模式下的SPWM控制及MS切换控制均由DSP实现。

图3　静止式中频电源组网过程中带本地负载模式原理Fig.3　Principle of integration of the power supply with local load

SSS闭合前静止式中频电源组网单元工作在独立模式，内部控制采用双闭环多重比例谐振（Multiply Dual-Loop Proportional-Resonant，MDLPR）控制向本地负载供电，同时采用过零点检测技术由DSP检测电网电压过零点，并通过数字锁相环技术实现组网单元对电网电压相位的跟踪。当上位机下达允许并网指令后，组网单元控制算法由MS控制切换为电流环控制模式，同时闭合SSS使组网单元在电网电压过零点处接入电网，实现电源由独立带载模式向组网运行模式的转换。在组网运行模式下，组网单元输出功率的一部分供给本地负载，其余馈送给其他挂网负载。当上位机下达脱网指令后，SSS断开并将组网单元控制算法切换为MDLPR控制模式，电源工作于独立模式，继续不间断向本地负载供电。

在静止式中频电源组网或者脱网的工作模式切换过程中，可能出现较大的电压或电流冲击，这对于中频电网、负载及中频电源本身都是不利的。理论上来讲，MS和SSS同步切换时，冲击最小，但实际过程中，由于系统及开关动作时延等因数，MS和SSS几乎不可能实现同步，因此，在组网或者脱网过程中，控制上必须给出一个明确的先后顺序，该顺序决定了模式切换过程中电压、电流的冲击大小，而该顺序的确定可以通过模式切换的暂态分析来决定。

2　组网系统模式切换暂态分析

静止式中频电源组网系统组网单元独立运行和组网运行的等效电路如图4所示。ZL为本地负载，下面分别以MS先于SSS闭合（或断开）、SSS先于MS闭合（或断开）两种开关顺序进行模式切换的暂态分析。

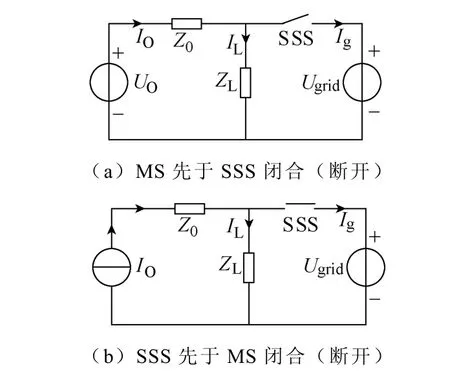
图4　静止式中频电源组网单元独立、组网运行等效电路Fig.4　Equivalent circuit of independent and integration

2.1模式开关先于静态开关闭合（或断开）

图5为MS先于SSS闭合情况下静止式中频电源组网时模式切换过程。t1和t2分别为MS和SSS闭合的初始时刻。在t1时刻前，组网单元处于MDLPR控制模式（电压源模式），为独立带载运行状态；在t1时刻，MS闭合，组网单元切换为单电流环控制模式（电流源模式），且在t2时刻前SSS仍为断开状态，因此，这里t1和t2时刻之间出现一个模式切换过渡状态。在t1时刻前，锁相环跟踪控制已使UO=Ugrid，组网单元输出电流IO取决于本地负载ZL的需要，即IO=IL；从t1时刻起，电流环给定突变为组网电流给定值，即IO=Iref，在t1～t2区间，SSS尚未闭合情况下，IO全部流入本地负载ZL，导致负载端电压UL出现幅值过冲

图5　MS先于SSS闭合情况下，中频电源组网时模式切换过程Fig.5　The conversion process of MS turned on before SSS

实际上，式（1）中UL受静止式中频电源直流侧电压幅值的限制，其过冲也会受到限制，IO和Ig畸变程度有限。从t2时刻起，SSS闭合，组网单元转为电流源输出控制模式，整个系统处于组网运行模式，电流环给定保持不变，UL被强制降为Ugrid，组网单元输出电流IO的一部分流入本地负载ZL维持其正常工作，其余则馈入电网，此时有

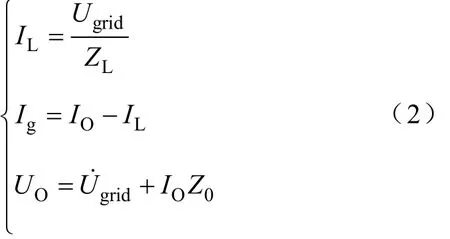
图6为MS先于SSS断开情况下，静止式中频电源脱网时模式切换过程。脱网过程中，从t3时刻起，MS先于SSS断开，组网单元控制模式由电流环转换为MDLPR输出控制模式，但由于SSS仍保持闭合，造成组网单元与电网并联，共同分担负载电流的中间过渡状态。在t3时刻前，组网单元处于组网运行状态，有

在t3～t4区间，MS断开但SSS仍为闭合状态，即UL仍被钳制为Ugrid，电压环PR调节器输出为饱和值，此时，极易形成瞬时环流。从t4时刻起，SSS断开，UL不再被Ugrid钳制，电压环PR调节器退出饱和状态，组网单元切换为独立工作模式，为本地负载不间断供电。

图6　MS先于SSS断开情况下，中频电源脱网时模式切换过程Fig.6　The conversion process of MS turned off before SSS

2.2静态开关先于模式开关闭合（或断开）

图7为SSS先于MS闭合情况下，静止式中频电源组网时模式切换过程。在t5时刻SSS闭合，UL立即被钳制为Ugrid，由于MS处于断开状态，组网单元仍以MDLPR电压源输出控制模式运行，直至t6时刻MS闭合，t5～t6时刻中间过渡状态与图6中t3～t4时刻过渡状态相同，这里不再赘述，如图7所示。t6时刻MS闭合，组网单元切换为单电流环输出控制模式，整个系统进入组网运行状态，负载端电压保持不变。此时，式（2）依然成立。

图7　SSS先于MS闭合情况下，中频电源组网时模式切换过程Fig.7　The conversion process of SSS turned on before MS

图8为SSS先于MS断开情况下，静止式中频电源脱网时模式切换过程。脱网过程中，从t7时刻起，SSS先于MS断开，组网单元和本地负载与电网脱开，且在t8时刻前MS仍保持闭合状态，组网单元以组网电流Iref为给定值，继续在电流源控制模式下工作。其输出电流IO全部灌入本地负载，该中间状态与图5中t1～t2时刻的中间过渡状态相同。从t8时刻起，MS断开，组网单元开始以MDLPR模式独立为本地负载供电。

图8　SSS先于MS断开情况下，中频电源脱网时模式切换过程Fig.8　The conversion process of SSS turned off before MS

由上述分析可以看出，以静止式中频电源组网单元电压源输出控制状态作为中间过渡的组网/脱网过程中（组网时SSS先闭合，脱网时MS先断开），负载电压突变较小，但极易形成环流冲击，存在安全隐患。由于MDLPR控制中电压环调节器饱和作用影响，使得组网过程中电源承受较大的冲击。若以组网单元电流源输出控制状态作为中间过渡的组网/脱网过程（组网时MS先闭合，脱网时SSS先断开），虽然负载电压突变次数较多，但因组网单元直流侧电压的幅值限制了输出电压突变的幅值，不会威胁组网单元的安全，而且在中间过渡状态电源工作相对稳定。

因此，对于静止式中频电源组网系统带载情况下，模式切换过程应采用组网时MS先闭合，脱网时SSS先断开的开关顺序。

3　组网系统模式切换平滑控制

通过前述静止式中频电源组网系统模式切换的暂态分析，确定了MS和SSS在组网及脱网过程中的开关顺序，但如何保证组网单元在组网和脱网过程中以较小的电流冲击实现模式切换的平稳过渡，关键取决于组网系统模式切换暂态过程的控制。为此，本文提出一种静止式中频电源组网系统模式切换平滑控制策略，下文以图9所示的组网系统为基础，分析模式切换平滑控制算法的要点。

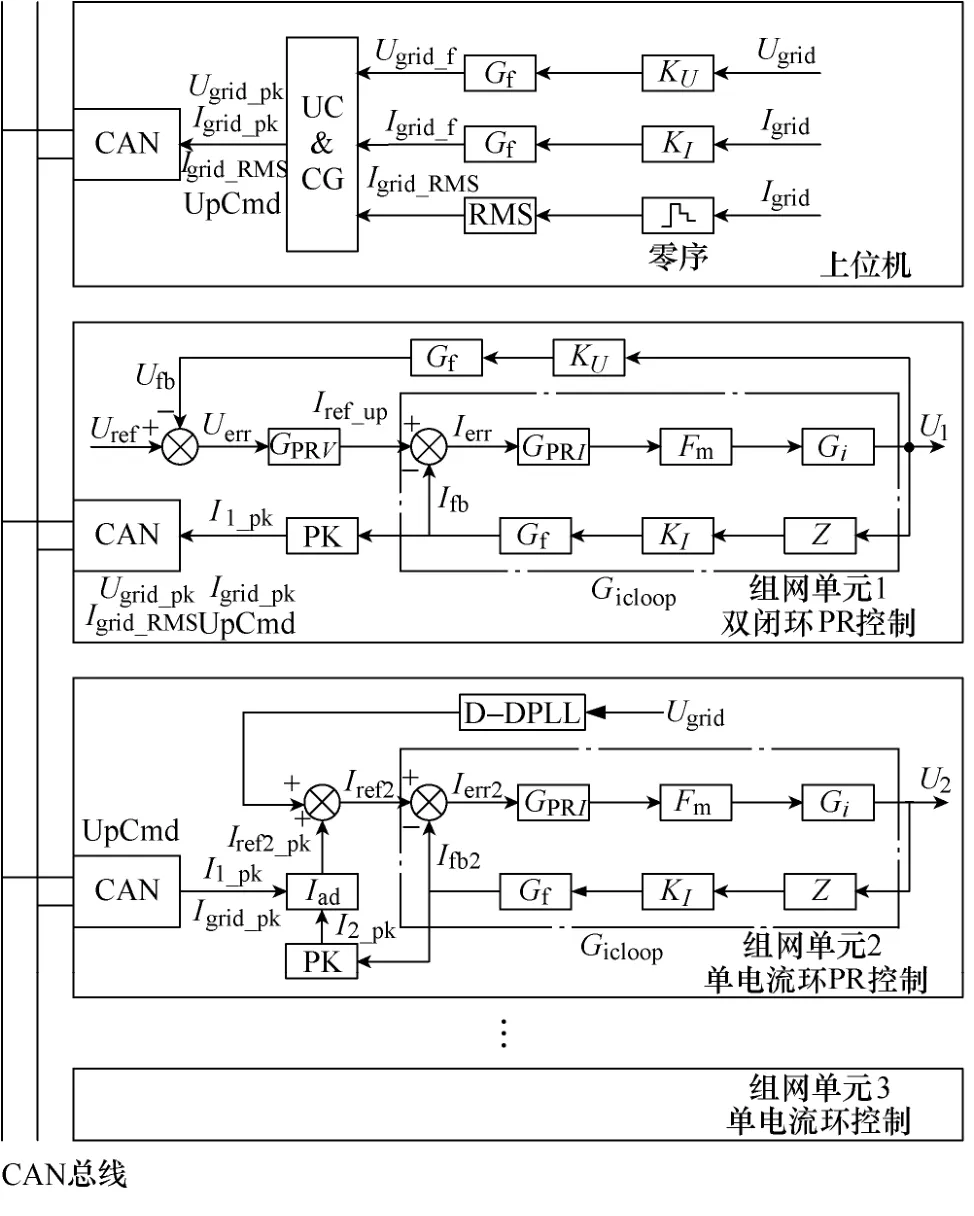
图9　静止式中频电源组网系统框图Fig.9　The solid-state power supply integration system

图9为静止式中频电源组网系统框图。其中，Gf为低通滤波器；KU为电网电压反馈增益；KI为电网电流反馈增益；UpCmd为上位机指定MDLPR控制指令；Iad为组网中频电源电流参考调节器；Z为负载阻抗；Ugrid、Igrid分别为电网电压和电网输出总电流；Ugrid_pk、Igrid_pk和Igrid_RMS分别为电网电压、电流峰值和网侧电流有效值；U1、U2分别为组网单元1和2的输出电压；I1_pk、I2_pk分别为组网单元1和2输出电流的峰值；Fm为DSP调制比；UC&CG为上层控制器逻辑及数字运算模块；PK为电流峰值计算模块。文中的MDLPR控制策略为［14，15］

式中，GPRV、GPRI分别为电压外环和电流内环PR控制器；Kpv、Kpi分别为电压、电流环的比例系数；Kivn、Kiin分别为电压、电流环的谐振系数，n为需要调节的谐波次数；ωc为谐振控制器的截止角频率；ω0为基波角频率。

从图9中可以看到每个独立中频电源都含DSP控制系统，上位机负责提供电源的运行模式和并网中频电源电流参考。当静止式中频电源由独立运行状态切换至组网运行模式时，中频电源由MDLPR控制切换到单电流环PR控制。在组网过程中，至少有一台中频电源运行在MDLPR控制状态，其余的中频电源运行在单电流环PR控制模式。运行在MDLPR控制的中频电源由上位机通过CAN总线决定。当处于MDLPR控制运行模式的静止式中频电源出现故障时，上位机通过及时检测电网信号，指定由下一台中频电源运行于MDLPR控制模式。

为了减小整个组网系统的环流，组网系统必须在整个组网单元中很好地均分输出电流。在图9中，上位机通过UpCmd命令指定主机运行模式，将检测到的电网输出电流Igrid通过UC&CG计算得到Igrid_pk，并将Igrid_pk通过CAN总线共享给所有组网单元。组网单元从机的电流峰值Iref2_pk由Igrid_pk、I1_pk及I2_pk通过Iad调节器共同决定，具体调节方式为

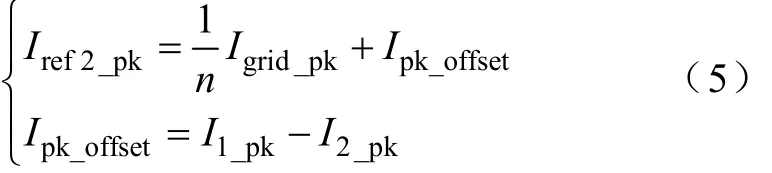
式（5）的约束条件为

式中，Ipk_offset为组网单元之间的峰值电流差；ΔIpk为峰值电流差约束范围；Ipk_step为峰值调节步长，在实际DSP运算中相当于在峰值电流差大于约束范围时，对Ipk_offset进行PI调节，主要目的是保证电流幅值的平滑调节。上述过程即为组网过程中的无功调幅过程。

同理，组网单元从机的参考电流相位Iref2_θ由D-DPLL输出相位Ipll_θ和从机输出电压相位U2_θ共同决定，具体调节方式为

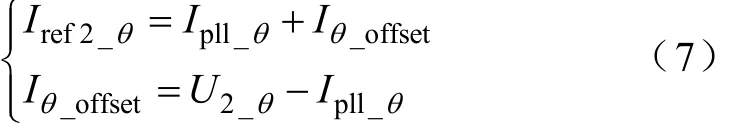
式（7）的约束条件为

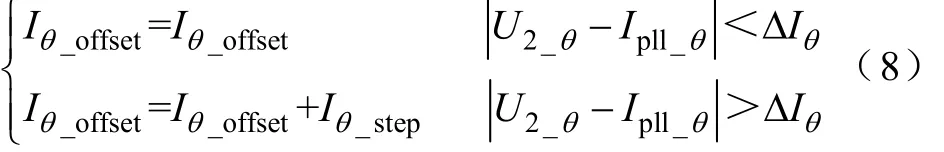
式中，Iθ_offset为组网从机单元锁相输出相位与实际输出电压相位差；ΔIθ为相位差约束范围；Iθ_step为相位调节步长，在实际DSP运算中相当于在相位差大于约束范围时，对Iθ_offset进行PI调节，主要目的是保证相位的平滑调节。上述过程即为组网过程中的有功调相过程。

由式（5）和式（7）可得组网从机单元的电流环参考表达式

推广到第n台组网单元电流环参考表达式为

式中

上述算法保证了组网系统电流峰值和相位的平滑调节，模式切换平滑控制算法还必须遵循以下原则：开关动作期间避免引起较大的负载端电压尖峰和电流冲击；SSS闭合前，保证组网单元输出电压在幅值、相位及频率上与电网电压同步匹配。

为此，组网单元由独立运行到组网运行的平滑控制算法步骤如下：

（1）上位机监测由主机构成的中频电网输出电压Ugrid是否满足组网要求，并实时计算Ugrid_pk、Igrid_pk和Igrid_RMS，通过CAN总线将信息传输给各组网单元。

（2）组网单元内部通过数字锁相环保证输出电压对电网电压的锁相跟踪，保证输出电压在幅值、相位及频率上与电网电压一致。

（3）上位机通过CAN总线发送组网指令UpCmd_1，从机单元一旦确认并网指令，首先闭合MS，将输出控制模式从MDLPR控制转换为单电流环控制，组网从机单元输出电流给定初值Irefn_pk。

（4）在电网电压过零点处闭合SSS。

（5）通过式（5）和式（7）同步调整Irefn_pk和Irefn_θ，保证组网单元对电网的同步跟踪。

同理，组网单元由组网运行到独立运行的平滑控制算法步骤如下：

（1）上位机实时监测组网系统电压Ugrid和Igrid，判断电网的运行状态，并通过CAN总线发送脱网指令UpCmd_0。

（2）一旦确认脱网指令要求，为了减小SSS分断时馈入电网电流Ig的冲击，组网从机单元首先将输出电流Irefn_pk降为本地负载电流。

（3）在电网电压过零点处分断SSS。

（4）模式开关MS断开，组网从机单元从单电流环控制模式转换为MDLPR控制模式，给本地负载不间断供电。

4　仿真与实验分析

为了更加清楚地说明文中暂态分析的正确性以及验证模式切换暂态过程控制的有效性，本文采用三台容量为100kV·A，输出电压115V/400Hz三相四线制中频电源进行了仿真和实验分析。其中一台作为主机运行于MDLPR控制模式，由其首先构建中频电网。

图10为静止式中频电源组网系统组网过程中不带本地负载的组网仿真过程。图10a为组网系统电网电压、电流及组网从机输出电流波形。从图中可以看出，组网过程从20ms处开始，组网主机电压Ugrid在30ms处（即10ms内）恢复正常，主机电源电流i11（即Igrid）由297A降为单机运行时的1/3左右，稳态输出电流100A；两台组网从机电源输出电流i11亦经过10ms调整，稳态输出电流分别为97.6A和99.4A。图10b为组网系统A、B和C各相环流，从图中可以看出，各相环流的瞬时最大峰值均小于100A，稳态环流为3.5A，满足组网系统要求。

图10　组网过程中不带本地负载Fig.10　Integration without local load

图11　带本地负载情况下，模式切换顺序错误时组网及脱网暂态过程Fig.11　Transient process with wrong mode convertion sequence with local load

图11为静止式中频电源带本地负载情况下模式切换顺序错误时A相组网/脱网暂态过程。从图11a可以看出，SSS于0.02s处闭合，MS于0.03s处闭合（即SSS先于MS闭合）时，电网电压Ugrid及组网单元输出电压UO1的电压波动次数较少，但其馈入电网的电流Ig的冲击太大，形成较大环流，实际中将导致组网失败。从图11b可以看出，MS于0.08s处断开，SSS于0.09s处断开（即MS先于SSS断开）时，馈入电网电流Ig瞬时增大到几千安培，导致电网电压Ugrid及组网单元输出电压UO1的电压发生严重畸变和超调，实际使用中可能导致设备的损坏。图11的现象与前述模式切换暂态过程分析一致，证明了理论分析的正确性。

图12　带本地负载情况下，采用模式切换平滑控制时组网及脱网过程仿真结果Fig.12　Simulation results of mode conversion with smooth control with local load

图12为带本地负载情况下采用模式切换平滑控制（组网时MS先闭合，脱网时SSS先断开）时，静止式中频电源组网及脱网过程，图中以A相为例，其他类似。图12a为组网过程，MS在0.02s处闭合，SSS在0.03s处闭合，图中波形从上到下依次为电网电压Ugrid、组网从机输出电压UO1、主机输出电流Igrid、组网从机输出电流IO1、本地负载电流IL和组网从机馈入电网电流Ig。组网前主机带满载运行Igrid为290.6A，从机带本地负载（半载）运行IO1为145.3A。当MS闭合SSS断开时（0.02～0.03s），由于从机电源并未与主机连接，因此，Ugrid及Ig没有变化；在0.02s处UO1、IO1及IL开始出现增幅波动，但增幅逐步衰减，这是由于组网从机单元由MDLPR控制切换为单电流环控制，电流环给定值突变为组网参考电流，IO1全部流入本地负载所致，同时UO1受直流侧的约束增幅受限，与前述理论分析一致；在0.03s处SSS闭合，UO1降为与Ugrid一致进入稳态输出，组网从机输出电流IO1由145.3A增大为219.2A，其一部分继续供给本地负载IL，另一部分馈入电网，给主机减轻负担，Igrid由290.6A减小为218.9A，此后Igrid与IO1均分组网系统的电流。图12a与图11a相比，虽然Ugrid和UO1的波动次数增加，但整个暂态过程中系统运行稳定，且馈入电网电流Ig最大瞬时峰值为230A，冲击较小，稳定运行时Ig为73.6A供给挂网负载。

图12b为脱网过程，SSS在0.08s处断开，MS在0.09s处断开，图中波形从上到下与图12a相同。在SSS分断前，0.078s处组网从机电流环参考减为本地负载电流，保证SSS分断时Ig不出现大的冲击，如图12b中IO1及Ig的波形所示。当SSS断开MS仍闭合时（0.08～0.09s），Ugrid、IL及UO1没有出现较大波动，Ig降为0，同时IO1由219.2A减小为145.3A，Igrid由218.9A增大为290.6A。当MS断开后，组网从机单元由单电流环控制切换为MDLPR控制，继续不间断给本地负载供电。与图11b相比，整个脱网暂态过程较为稳定，无大的电流冲击及电压瞬变。图12的整个组网及脱网过程证明了模式切换平滑控制的良好性能。

图13为采用模式切换平滑控制时，静止式中频电源组网及脱网过程实验结果，图中以A相为例。图13a为组网过程，MS先于SSS闭合，且闭合点均在电网电压过零点处，图中波形从上到下顺序与仿真波形相同。组网前主机带满载运行Igrid为289.5A，从机带本地负载（半载）运行IO1为144.8A。当MS闭合SSS断开时（图中虚线所示区域），由于从机电源未与电网主机连接，Ugrid及Ig没有变化；由于组网从机单元由MDLPR控制切换为单电流环控制，电流环给定值突变为组网参考电流，IO1全部流入本地负载导致UO1、IO1及IL出现波动（椭圆形区域），与仿真结果一致；当SSS闭合后，UO1降为Ugrid进入稳态输出，组网从机输出电流IO1由波动状态进入稳态，输出电流有效值由144.8A增大为218.7A，其一部分继续供给本地负载IL，另一部分则馈入电网，相当于给主机减轻负担，Igrid由289.5A减小为219.4A，此后Igrid与IO1均分整个组网系统的电流；馈入电网电流Ig的最大瞬时峰值为239A，较仿真稍大，稳定运行时Ig为71.2A馈入挂网负载。

图13　采用模式切换平滑控制时，组网及脱网过程实验结果Fig.13　Experiment results of mode conversion with smooth control

图13b为脱网过程，SSS先于MS断开（图中虚线部分）。在SSS分断前一个周期（程序设置）组网从机电流环参考减为本地负载电流，图中IO1及Ig波形圆形区域中出现短时电流波动，在MS切换后波动消失，与仿真结果一致。在中间暂态过程中，SSS断开，Igrid由219.4A增大为289.5A，电网电压Ugrid稍有跌落（峰值3V）相当于突加负载。同时IO1由218.7A减小为144.8A，UO1无明显变化。当MS断开后，组网从机单元由单电流环控制切换为MDLPR控制，继续不间断给本地负载供电。

对比图13和图12可以看出，实验与仿真结果基本一致，进一步证明了理论分析的正确性和模式切换平滑控制在中频电源组网系统中的有效性。

图14为三台100kV·A静止式中频电源组网系统稳态运行实验结果，组网系统总输出容量达333kV·A。图14a为主机各相输出电压、电流，可以看出虽然负载不平衡，但输出电压平衡度较高，单机输出容量达111kV·A；图14b为电网电压有效值、频率及前50次谐波分布，从中可以看出电压频率为400.5Hz，THD为1.5%，满足系统输出要求；图14c为主、从机三相输出电流，可以看出即使负载不平衡，但电流均分程度较好；为了更直接地说明各台电源电流均分程度，将主机A、B和C相输出电流与从机2A、2B和2C相输出电流进行对比，如图14d所示，从中可以看出电流幅值和相位一致性较好，表明组网系统具有良好的稳态运行性能。

图14　三台静止式中频电源组网运行稳态实验结果Fig.14　Experiment results of integration of three solid-state power supplies

5　结论

本文通过详细分析不同开关顺序对静止式中频电源组网系统模式切换暂态过程的影响，得出组网时MS先闭合、脱网时SSS先分断为最优开关顺序的结论。同时，结合该结论提出一种峰值和相位平滑调节的组网系统模式切换控制策略，并给出具体实施步骤。从仿真和实验结果可以看出，该组网系统在并、脱网过程中电网电压波动及馈入电网电流冲击均较小，稳态运行时电流均分程度较好，证明了文中理论分析及控制方法的正确性。

［1］ 朱俊杰，马伟明，聂子玲，等. 静止式中频电源谐波分析及抑制方法研究［J］. 电力自动化设备，2012，32（10）： 77-82.

Zhu Junjie，Ma Weiming，Nie Ziling，et al. Research on harmonic analysis and suppression for static medium frequency inversion power supply［J］. Electric Power Automation Equipment，2012，32（10）：77-82.

［2］ 刘春喜，马伟明，孙驰，等. 大功率400Hz逆变电源数字控制设计［J］. 电工技术学报，2011，26（1）：100-107.

Liu Chunxi，Hu Wenhua，Sun Chi，et al. Digital control design of high power 400Hz inverters［J］. Transactions of China Electrotechnical Society，2011，26（1）： 100-107.

［3］ Li Chen，Ji Shiming，Tan Dapeng. Multiple-loop digital control method for a 400Hz inverter system based on phase feedback［J］. IEEE Transactions on Power Electronics，2013，28（1）： 408-417.

［4］ 刘其辉，谢孟丽. 双馈式变速恒频风力发电机的空载及负载并网策略［J］. 电工技术学报，2012，27（10）：60-67.

Liu Qihui，Xie Mengli. Strategies of grid-connection of doubly-fed variable-speed constant-frequency wind power generator with no-load and with load［J］. Transactions of China Electrotechnical Society，2012，27（10）： 60-67.

［5］ Nathaniel B，Milan P，Timothy G. Dynamic stability of a microgrid with an active load［J］. IEEE Transaction on Power Electronics，2013，28（11）： 5107-5119.

［6］ Lee C T，Jiang R P，Cheng P T. A grid synchronization method for droop-controlled distributed energy resource converters［J］. IEEE Transaction on Power Electronics，2011，49（2）： 954-962.

［7］ Guerrero J M，Lee L T，Chandorkar M，et al. Advanced control architectures for intelligent microgrids-part II： Power quality，energy storage，and AC/DC microgrids［J］. IEEE Transaction on Industrial Electronics，2012，58（6）： 1156-1165.

［8］ 蒋冀，段善旭，陈仲伟. 三相并网/独立双模式逆变器控制策略研究［J］. 电工技术学报，2012，27（2）：52-58.Jiang Ji，Duan Shanxu，Chen Zhongwei. Research on control strategy for three-phase double mode inverter［J］. Transactions of China Electrotechnical Society，2012，27（2）： 52-58.

［9］ Guerrero J M，Lee L T. Power quality in microgrids and distribution power systems［C］. The 21st IEEE International Symposium on Industrial Electronics，Hangzhou，2012： 978-986.

［10］ 唐西胜，邓卫，齐志平. 基于储能的微网并网/离网无缝切换技术［J］. 电工技术学报，2011，26（1）： 279-284.

Tang Xisheng，Deng Wei，Qi Zhiping. Research on grid-connected/islanded seamless transition of microgrid based on energy storage［J］. Transactions of China Electrotechnical Society，2011，26（1）： 279-284.

［11］ 陈晓，孙以泽，孟嫜. 独立/并网双工模式光伏逆变系统的设计［J］. 电力电子技术，2012，46（1）： 56-60.

Chen Xiao，Sun Yize，Meng Zhang. Design on stand-alone/grid-connected photovoltaic inverter system［J］. Power Electronics，2012，46（1）： 56-60.

［12］ Tang Xisheng，Deng Wei，Qi Zhiping. Investigation of the dynamic stability of microgrid［J］. IEEE Transaction on Power Electronics，2014，29（2）： 698-706.

［13］ 李子欣，王平，李耀华，等. 采用数字控制的400Hz大功率逆变电源［J］. 中国电机工程学报，2009，29（6）： 36-42.

Li Zixin，Wang Ping，Li Yaohua，et al. 400Hz high-power voltage-source inverter with digital control［J］. Proceedings of the CSEE，2009，29（6）：36-42.

［14］ Zhu Junjie，Nie Ziling，Ma Weiming，et al. Comparison between DB control and dual-loop PR control for collapsed H-bridge single-phase 400Hz power supply［C］. The 21st IEEE International Symposium on Industrial Electronics，Hangzhou，2012： 240-245.

［15］ 朱俊杰，马伟明，聂子玲，等. 一种用于静止式中频电源的比例谐振控制策略［J］. 电机与控制学报，2012，16（10）： 79-85.

Zhu Junjie，Ma Weiming，Nie Ziling，et al. A proportional-resonant strategy for static medium frequency［J］. Electric Machines and Control，2012，16（10）： 79-85.

Control of Mode Conversion Transient Process of
Medium Frequency Solid-State Power Supply

Zhu JunjieNie ZilingMa Weiming
（National Key Laboratory for Vessel Integrated Power System Technology Naval University of EngineeringWuhan430033China）

The mode conversion transient process is very important to the 400Hz solid-state power supply integration system. For this reason，this paper analyzes the principle of network building，its independent operation with or without local loads during the integration process，and the effects of different switching sequences on mode conversion transient process. The conclusion is that the mode switch （MS） must turn on before the solid-state switch （SSS） at the on-grid state，while the SSS must turn off before the MS at the off-grid state. Therefore，a strategy of smooth control for the system which includes some concrete steps is proposed. It can achieve grid connection without shock by the average distribution of peak currents and smooth the adjustments of peak current and phase. Case study has verified the method for smooth control.

Medium frequency solid-state power supply integration system，mode conversion，switching sequence，transient process，smooth control

TM461.5

朱俊杰男，1984年生，助理研究员，博士，主要从事电力电子与电力传动等研究。

聂子玲男，1975年生，教授，博士生导师，主要从事电力电子与电力传动等研究。

国家自然科学基金资助项目（51177170）。

2014-03-10改稿日期 2014-05-16