LCL并网滤波器的非线性阻尼控制

杨仁增　张光先

（山东大学控制科学与工程学院　济南　250061）

LCL并网滤波器的非线性阻尼控制

杨仁增张光先

（山东大学控制科学与工程学院济南250061）

为提高LCL滤波并网变换器的控制性能，提出一种基于反馈线性化的LCL并网滤波电路级联非线性有源阻尼控制策略。该策略在三相LCL滤波并网变换器的仿射非线性模型基础上，采用级联的状态反馈线性化非线性控制方法，通过变换器网侧和桥臂侧有功电流、无功电流的全局线性化精确解耦控制，实现LCL滤波器的有源阻尼。所提非线性级联控制策略可消除LCL滤波电路的谐振尖峰，提升并网变换器的整机控制性能。仿真和实验验证了该控制策略的正确性和可行性。

LCL并网滤波器有源阻尼非线性控制反馈线性化

0　引言

为抑制整流器、逆变器等并网功率变换器中功率器件开关产生的高次谐波，需在变换器与电网间接入滤波电路。为得到较好的谐波抑制效果，国内外学者广泛采用LCL滤波电路进行电压源型并网变换器整机系统的设计[1-10]。同样谐波标准和功率器件开关频率下，相比于L滤波电路，LCL滤波电路可采用较小的滤波电感设计，有效减小系统体积，并降低能量损耗。然而，LCL滤波电路具有三阶特性，其频率响应在谐振频率处存在谐振尖峰，且相位发生180°跳变，易造成并网变换器振荡甚至引起不稳定，因此LCL并网滤波器应用的主要问题是对滤波电路的谐振尖峰进行阻尼[3-6]。

LCL滤波电路谐振尖峰的阻尼方法包括无源阻尼和有源阻尼两大类。无源阻尼的基本方法是在滤波电感或滤波电容上串联或并联电阻，具有实现简单、不受开关频率限制等优点，但会产生额外的能量损耗。有源阻尼方法通过引入合适的滤波电感或滤波电容的电压、电流等状态变量的反馈控制，实现谐振尖峰的抑制，没有额外的能量损耗[5-10]。

目前的LCL滤波并网变换器中，广泛采用滤波电容电流比例反馈的有源阻尼方法，该方法须在合适的LCL滤波器谐振频率和系统控制频率比率范围内，才能保证系统的稳定性并有较好的控制性能［5］。影响系统控制频率的PI调节器参数和电容电流反馈系数等闭环控制参数，可通过对主导极点的配置［5］或绘制奈奎斯特图[8]等方法来求取，这些设计方法都需反复试凑才能求得使系统具有理想控制性能的闭环参数，且不易保证网侧阻抗变化等电网扰动下的系统控制鲁棒性[9]。文献[10]的研究表明，并网变换器工作于有源逆变模式时，其对于电网的等效谐波阻抗呈负阻特性，当电网公共耦合点存在电压波形畸变时，其与电网等效谐波阻抗间的相互影响将破坏整个系统的稳定性。常规线性PI调节的有源阻尼方法，网侧有功、无功电流不能实现完全的解耦控制，网侧电压和电流的有功、无功分量的相互扰动，造成系统各控制参数的选取顾此失彼，因而常规线性PI调节的有源阻尼方法并不能彻底消除LCL滤波电路的谐振尖峰。

以微分几何理论为基础的反馈线性化的非线性系统设计方法，通过选择适当的非线性状态和坐标变换，使非线性系统实现状态或输入/输出的精确线性化，从而可沿用经典线性系统的设计方法解决复杂的非线性系统综合问题。该方法与利用泰勒展开式进行局部线性化近似的小信号扰动法等方法不同，在线性化过程中没有忽略掉任何高阶非线性项，线性化对变换有定义的整个区域都适用[11]。国内外有学者将反馈线性化方法用于设计电力有源滤波器［12］、三相UPS电源[13]、控制永磁风力发电机[14]及光伏逆变器[15]等电力设备，都取得了明显优于经典PI线性控制策略的控制效果。

文献[16]的LCL滤波并网变换器反馈线性化设计，建立在滤波电容串联无源阻尼电阻的基础上，忽略了滤波电容的相关状态变量，等同采用L滤波并网变换器的反馈线性化设计方法，未能体现反馈线性化方法设计复杂非线性系统的优势。文献[17]的反馈线性化设计，实现了滤波电路谐振尖峰的有效阻尼，取得了优于常规PI线性控制策略的控制效果，但存在算法线性化反馈矩阵较为复杂的问题，不利于在运算资源有限的单片机及DSP等数字控制系统中工程应用。

本文提出的LCL并网滤波器非线性级联控制算法，采用反馈线性化方法设计变换器的桥臂侧电流环和网侧电流内环，实现变换器桥臂侧和网侧有功电流、无功电流的精确解耦控制，通过输入控制量的全局线性化调节以消除LCL滤波电路的谐振尖峰。仿真和实验表明，这种非线性级联控制结构物理意义明确、算法结构简洁，引入网侧电容电压状态信号而非电容电流状态信号实现LCL滤波器的阻尼控制，可有效提升LCL滤波并网变换器的整机控制性能。

1　LCL滤波三相并网变换器

1.1三相并网变换器

并网变换器较多采用电流内环和电压外环的PI调节前馈解耦的线性控制策略[1]，选择直流电压外环的控制周期远大于交流电流内环的控制周期，可实现直流母线电压调节与系统其他输入控制变量的近似解耦控制。

基于电网电压定向的控制策略，三相LCL滤波并网变换器电路结构如图1所示。图1中，Lg为网侧滤波电感，L为桥臂侧滤波电感，Cf为滤波电容。ej为电网相电压（j=a, b, c），ig为网侧电流，i为桥臂侧电流，uC为滤波电容电压。Cdc为直流母线电容，udc为直流母线电压，iL为直流母线负载电流。滤波电感、滤波电容的寄生电阻忽略不计。

图1　三相LCL滤波并网变换器Fig.1　Three-phase grid-connected converter with LCL filters

并网变换器采用空间矢量调制方法（Space Vector Pulse Width Modulation，SVPWM）[18]。为方便并网变换器数学模型的建立和推导，假设：①交流电源为三相三线平衡工频电源；②开关管开关频率固定，载波比远大于1；③L为平衡线性无饱和电感。

由电路功率守恒，可得基于同步旋转dq坐标系的LCL滤波并网变换器的状态空间方程如式（1）。式中，变换器参考电压ud、uq作为两个输入变量。系统（1）的控制输入数目小于系统的独立状态变量个数，控制输入的缺失使得LCL滤波并网变换器控制系统的设计具有较大的灵活性。

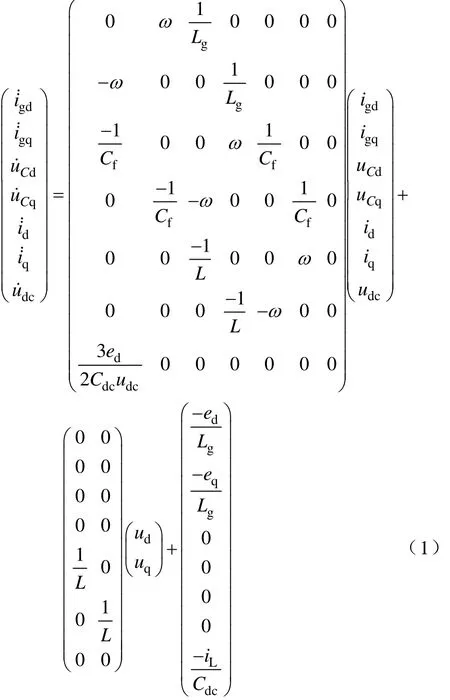
本文逆变器的直流电压控制直接采用常规PI调节，此处不再详述。将删除状态变量udc的系统（1）分解成两个子系统，第一个以桥臂侧电流作为输入控制信号，第二个以变换器调制指令电压作为输入控制信号，分别为

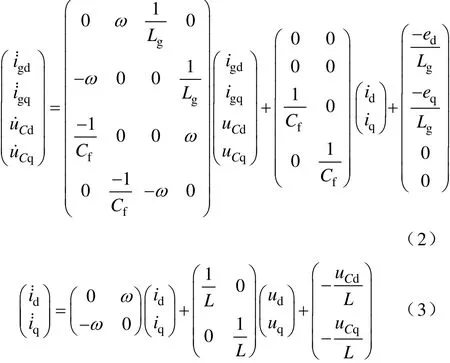
1.2LCL滤波器

图2a为并网变换器频域单相等效电路，图中LCL滤波电路的等效阻抗

图3为LCL滤波器含有源阻尼电路的频率响应示意图。由图3可见，LCL滤波器采用电容电流反馈的有源阻尼可使其谐振峰得到有效削减。

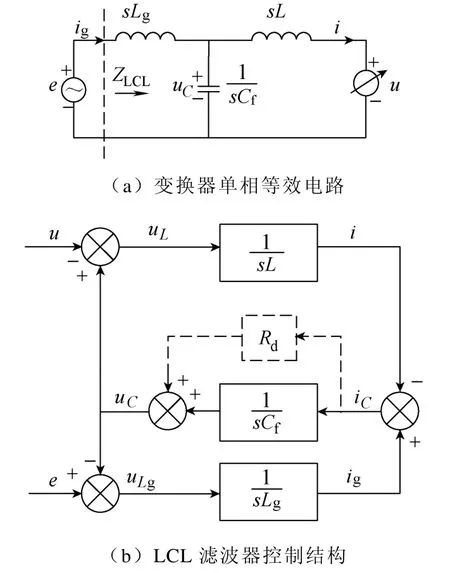
图2　变换器单相等效电路和LCL滤波器控制结构Fig.2　A per-phase equivalent circuit of the converter and control block diagram of LCL filters

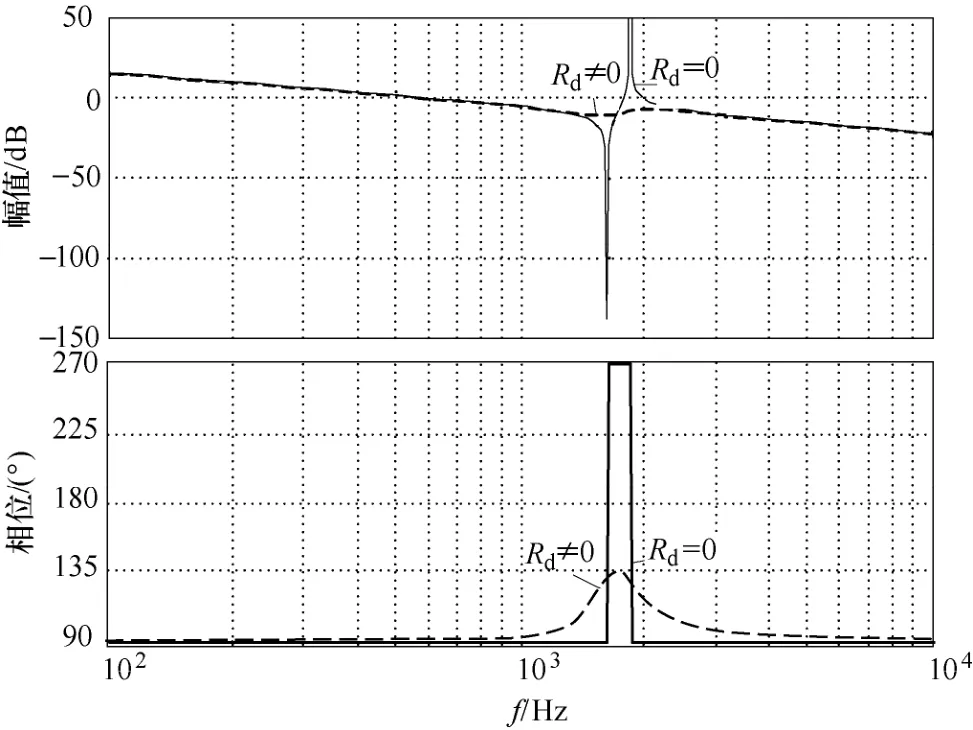
图3　LCL滤波器频率响应Fig.3　Frequency characteristics of LCL filters

采用电容电流反馈有源阻尼方法时，如果电容电流反馈系数过小，LCL滤波电路的谐振尖峰难以被有效阻尼；如果电容电流反馈系数过大，LCL滤波电路的谐振尖峰可得到有效阻尼，但会显著减小系统的相位裕度。

2　电流反馈线性化控制

2.1反馈线性化

反馈线性化理论的基本思路，是选择适当的非线性坐标变换z=T(x) 和非线性状态反馈量v=α(x)+β(x)u，使非线性系统得以在变量有定义的范围甚至全局范围内线性化。多变量输入、输出仿射非线性系统，在实现线性化的同时，可实现变量间的精确解耦[11]。

式（2）的状态方程，设状态变量x=(x1, x2, x3, x4)T=(igd, igq, uCd, uCq)T，输入变量u=(u1, u2)T=(id, iq)T，选择输出变量y=(h(x1), h(x2))T=(igd, igq)T。

设

为获得式（6）和式（7）所组成系统的输入、输出反馈线性化控制，对输出变量求导直至其导数式中首次出现输入变量，对式（7）求导可得

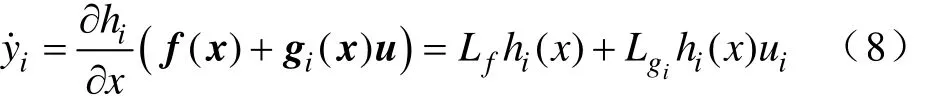
式中，Lfh、Lgh 分别为f(x)、g (x)的李导数。如果Lgh=0，输入变量与输出变量不相关，求导过程继续。经过r次求导，当条件满足

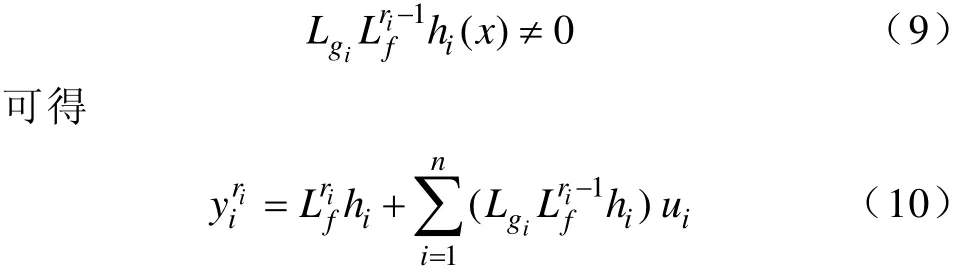
此时输入变量首次出现在输出变量导数式中。

对式（7）的两个输出变量都进行式（10）的求导过程，可得

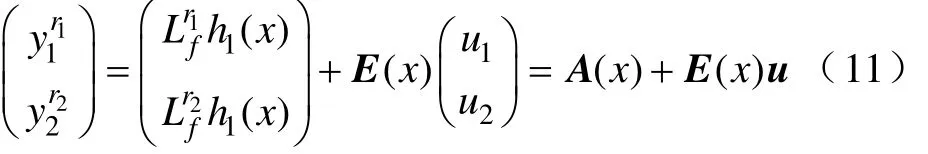
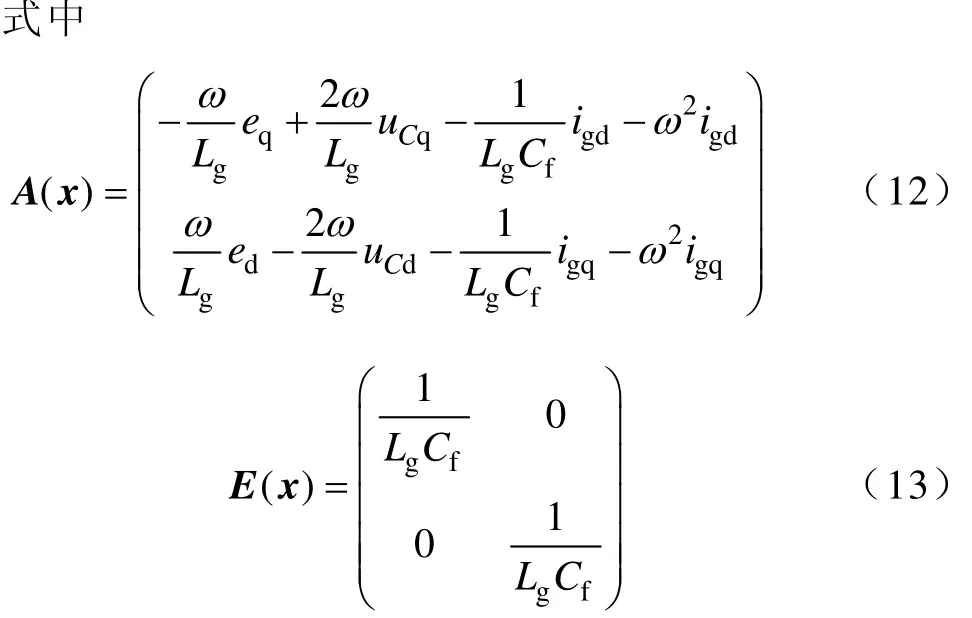
系统（11）的相对阶r1=r2=2，总相对阶r1+r2等于系统的状态变量个数，系统（11）可实现反馈线性化。式（13）的E(x)为解耦矩阵且可逆，选择新的控制输入变量

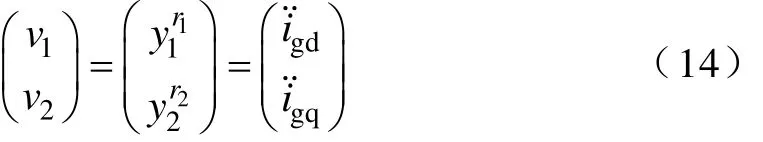
则可得如式（15）所示的反馈线性化控制。

为消除参数变化引起的误差，提高系统的鲁棒性，新的线性控制变量引入PI调节，即

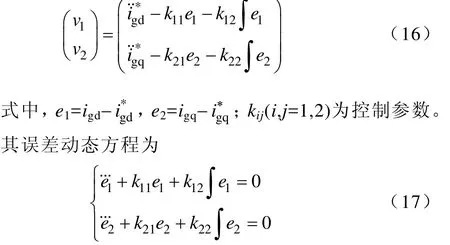
将式（17）的拉普拉斯变换方程的极点配置在左复半平面所需位置，便可计算出各控制参数kij。

式（3）系统只需一次求导，便可求得其输入变量与输出变量的关系。求解式（3）的反馈线性化控制的过程，与求解式（2）的过程相同，此处不再赘述。

图4所示为电流反馈线性化的控制框图，图中Ai(x)、Ei(x)表达式为

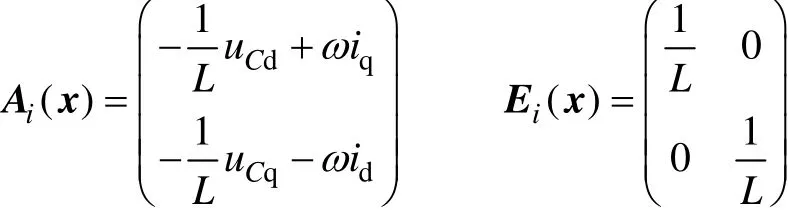
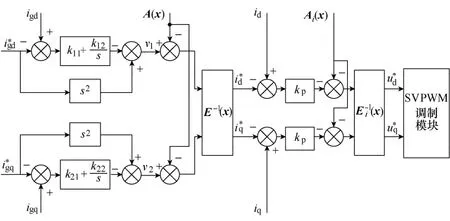
图4　电流反馈线性化控制框图Fig.4　Control block diagram for currents feedback linearization

图4中控制内环仅采用了比例调节，原因在于桥臂侧电流内环的稳态误差不会影响网侧电流外环的控制性能[3]。图4控制框图表明，采用反馈线性化控制，并网变换器的网侧电流和桥臂侧电流，均实现了有功分量与无功分量的精确解耦控制。

2.2桥臂侧电流估计

图4所示的反馈线性化控制，需测量的三相变换器4组网侧电力信号包括：电网电压信号、网侧电流信号、桥臂侧电流信号及滤波电容电压信号。为减少成本较高的交流电流传感器数目，采用文献[17]的电流估计方法，得桥臂侧电流估计运算式为

式中，k为离散采样点；Ts为采样控制周期。

3　仿真与实验结果

3.1系统仿真

利用Matlab/Simulink对LCL滤波并网变换器非线性控制进行计算机仿真。系统仿真框图如图5所示。

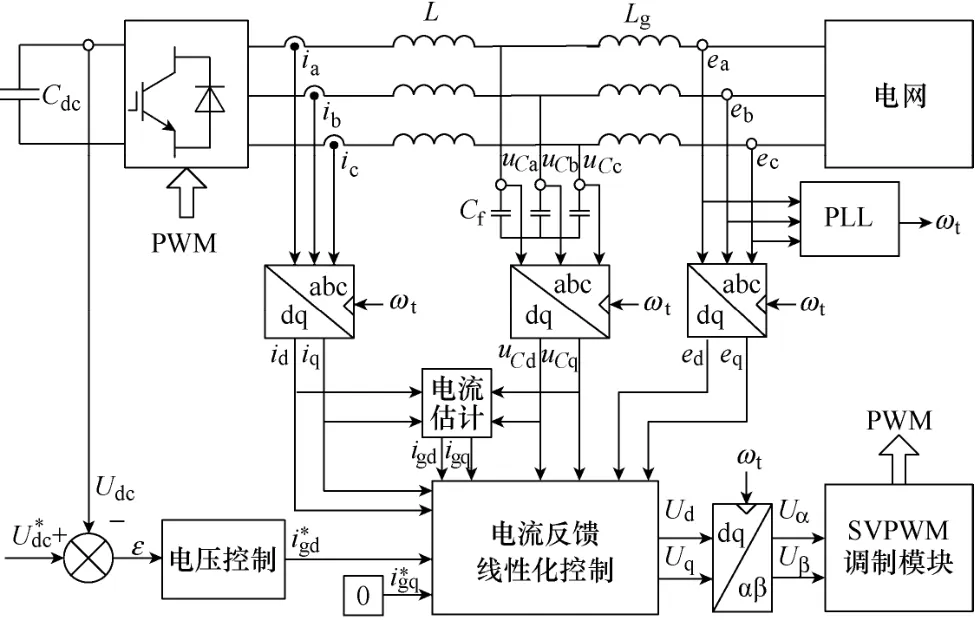
图5　LCL滤波并网变换器非线性控制仿真框图Fig.5　Simulation control block diagram for nonlinear controller of grid-connected converter with LCL fliters

三相电网电压仿真参数为220 V/50 Hz。LCL滤波器参数：Lg=0.6mH，Cf=16.0μF，L=2.0mH，其谐振频率为1 852 Hz。电网侧带15Ω交流负载，直流母线电压700V，Cdc=2 200μF。采样、控制频率均为6 kHz。

为对比非线性控制的性能，在主电路参数相同的情况下，同时对基于PI调节器前馈解耦、电容电流反馈有源阻尼的LCL并网变换器进行仿真。两种算法的控制参数见表1，表中电流环、电压环PI调节器参数由对称最优工程法得出[7]。

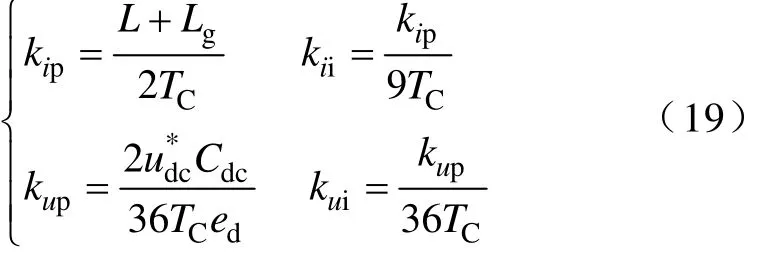
式中，TC为控制采样周期。

表1　变换器仿真控制参数Tab.1　Simulation parameters of inverter controllers

电容电流反馈支路阻尼电阻的取值

表1中非线性算法的控制参数kij，参照线性控制算法中kip、kii参数的取值，在两种算法的有功电流和无功电流的开环增益相同的要求下，经仿真优化获得。

由图4的电流反馈线性化控制框图，给出LCL滤波器在表1非线性控制参数下的电流环频率响应如图6所示，得到电流环幅值裕度为64.8dB，相位裕度为45°，非线性控制系统是闭环稳定的。图6表明，LCL滤波器电流环采用反馈线性化控制，其谐振尖峰已完全消除。

采用固定步长的离散仿真算法（步长6.667μs），仿真时长1s。检验两种控制策略在网侧负载扰动下的动稳态控制性能，当t= 0.7 s时，15Ω交流负载两端并联60Ω电阻，t= 0.8 s时拆除。

表2为两种控制算法的网侧A相电流谐波畸变率（Total Harmonic Distort，THD）比较数据。表中THD1为两种控制算法在t= 0.5～0.6 s内5个周波的THD，H37_1为相应的1 850 Hz谐波电流的幅值相对值；THD2为两种控制算法在t= 0.7～0.8 s内5个周波的THD，H37_2为相应的1 850 Hz谐波电流的幅值相对值。由表2可见，两种工况下的负载电流THD数值及谐振频率处的谐波电流值，非线性控制算法都明显低于PI调节有源阻尼控制算法。

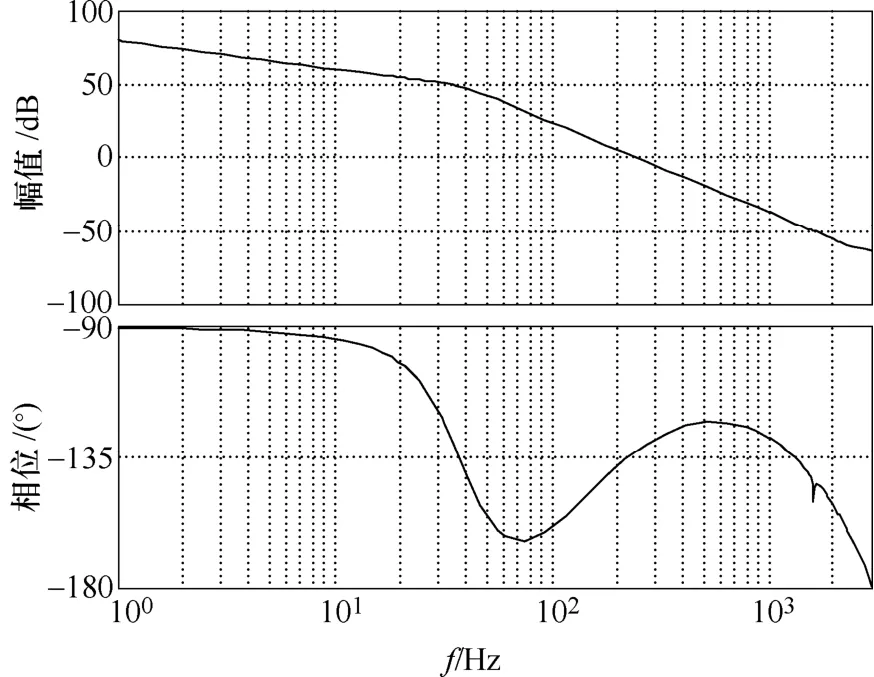
图6　非线性控制电流环频率响应Fig.6　Bode diagram for nonlinear current controllers

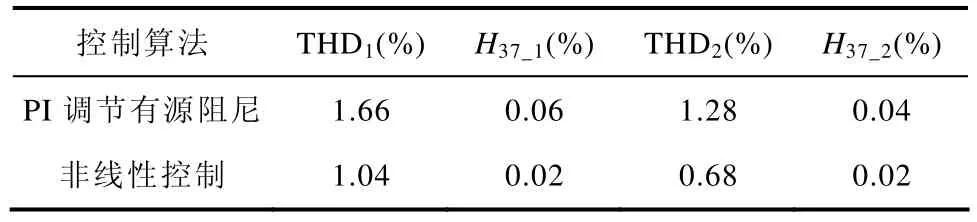
表2　两种控制算法网侧谐波电流比较Tab.2　Comparison of grid harmonics current between the two controllers

图7和图8为两种算法的网侧A相电压uga、网侧A相电流iga、网侧滤波电容电压dq分量uCd、uCq仿真波形。对比图7和图8仿真波形，图7的PI调节有源阻尼控制电容电压dq分量纹波较大，q轴分量稳态偏差大，图8的非线性控制电容电压dq分量纹波较小，q轴分量稳态偏差小。对比仿真可见，反馈线性化可对网侧电流与电压的有功分量和无功分量进行精确解耦控制，并具有较好的控制鲁棒性。

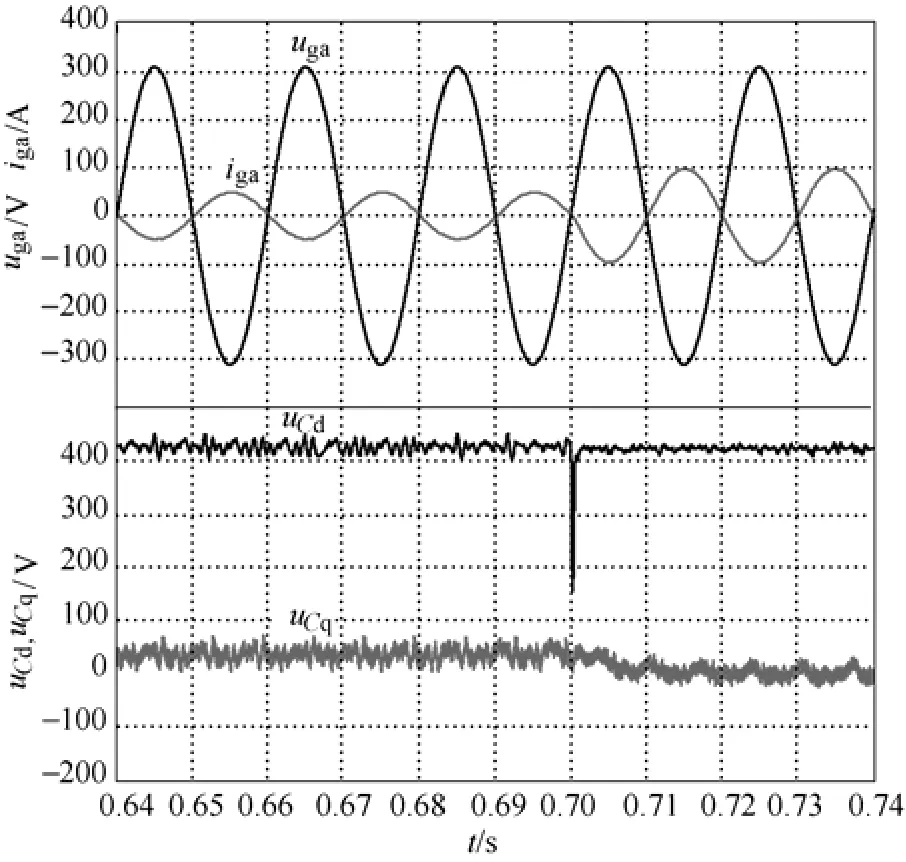
图7　PI控制有源阻尼仿真波形Fig.7　Simulation waveforms of PI controllers with active damping

图8　非线性控制仿真波形Fig.8　Simulation waveforms of nonlinear controllers

3.2实验

为验证非线性算法的可行性及有效性，搭建了一台20kW三相并网逆变器样机。实验样机由信号采样及调理电路、驱动及保护电路、控制电路和逆变主电路等几部分组成。主开关管选用三菱PM300CLA120模块。基于TI公司的浮点DSP TMS320F28335（主频150 MHz）设计控制系统，采样、控制频率为6kHz。交流电流通过电流霍尔LA-55P采样，交流电压通过LCTV31CE电压变换器采样。测试仪器为Agilent DS07014B示波器和Fluke43B谐波分析仪。

三相交流相电压为220 V/50 Hz。LCL滤波器：Lg=0.6×(1±5%)mH，Cf=16.0×(1±5%)μF，L=2.0× (1±5%)mH，交流负载为30×(1±5%)Ω。直流母线电压为700V，Cdc=2 200×(1±5%)μF。以网侧电流iga、电网电压uga及网侧滤波电容电压uCd、uCq实验信号为参照，对比检验LCL滤波并网逆变器采用PI调节前馈解耦有源阻尼控制与非线性控制的控制性能（PI调节有源阻尼算法同时采样网侧电流及网侧滤波电容电压信号）。两种算法的控制参数见表1的取值。

稳态时的交流侧THD，采用PI调节有源阻尼控制的A相电流THD为2.2%，其37次谐波电流相对值为0.04%，采用非线性控制的A相电流THD为1.6%，其37次谐波电流相对值为0.02%。

测试两种算法在交流参数扰动时的动态控制性能，实验中30Ω负载两端并联15×(1±5%)Ω负载，交流电流将短时由10A突变至30A。示波器输入通道：通道1为28335芯片ADCINA0端口的网侧A相电压采样信号uga-abc，通道2为采用Fluke i100s电流钳检测的网侧A相电流信号iga，通道3、通道4分别为28335运算后经DAC7724及其外围电路生成的，未加直流耦合量的网侧滤波电容电压dq分量信号uCd、uCq。

图9所示为PI调节有源阻尼控制实验波形，图中电容电压dq分量纹波较大，q轴分量稳态偏差大。图10所示为非线性控制实验波形，图中电容电压dq分量纹波较小，q轴分量稳态偏差较小。对比图9、图10可见，相比PI调节有源阻尼，非线性控制的系统控制鲁棒性较好，网侧电流与电压的有功分量与无功分量实现了精确解耦控制。

图9　PI控制有源阻尼实验波形Fig.9　Experiment waveforms of PI controllers with active damping

图10　非线性控制实验波形Fig.10　Experiment waveforms of nonlinear controllers

4　结论

本文提出的LCL并网滤波器级联非线性控制策略，算法的物理意义明确、控制鲁棒性强。在三相LCL滤波并网变换器仿射非线性模型的基础上，引入网侧电容电压状态信号，采用状态反馈线性化桥臂侧电流环及网侧电流环的级联控制结构，实现桥臂侧和网侧有功电流和无功电流的精确解耦线性化控制。该级联反馈线性环策略，其桥臂侧电流环中的比例控制可提高系统的响应速度，其网侧电流环中的比例积分控制器可消除系统参数变化引起的误差，提高系统的鲁棒性。级联非线性控制策略通过LCL滤波器的桥臂侧及网侧的有功电流和无功电流的精确解耦控制，通过输入控制量的全局线性化调节来实现其阻尼控制，可有效消除LCL滤波电路的谐振尖峰，提高了LCL滤波并网变换器的整机控制性能。

仿真和实物实验表明，本文提出的LCL并网滤波器非线性级联控制策略，易于数字实现，具有较好的工程实用意义。

[1] Loh P, Holmes D. Analysis of multiloop control strategies for LC/CL/LCL-filtered voltage-source and current-source inverters[J]. IEEE Transactions on Industrial Applications, 2005, 41(2): 644-654.

[2] 李欣然, 郭希铮, 王德伟, 等. 基于LCL滤波的大功率三相电压型PWM整流器[J]. 电工技术学报, 2011, 26(8): 79-84.

Li Xinran，Guo Xizheng，Wang Dewei，et al. Research and development of high-power three-phase voltage source PWM rectifier with LCL filter[J]. Transactions of China Electrotechnical Society, 2011, 26(8): 79-84.

[3] Twining E, Holmes D. Grid current regulation of a three-phase voltage source inverter with an LCL input filter[J]. IEEE Transactions on Power Electronics, 2003, 18(3): 888-895.

[4] Liserre M, Blaabjerg F, Hansen S. Design and control of an LCL-filter-based three-phase active rectifier[J]. IEEE Transactions on Industry Applications, 2005, 41(5): 1281-1291.

[5] Dannehl J, Fuchs F W, Hansen S, et al. Investigation of active damping approaches for PI-based currentcontrol of grid-connected pulse width modulation converters with LCL filters[J]. IEEE Transactions on Industrial Applications, 2010, 46(4): 1509-1517.

[6] Liu Fei, Zhou Yan, Duan Shanxu, et al. Parameter design of a two-current-loop controller used in a grid-connected inverter system with LCL filter[J]. IEEE Transactions on Industrial Electronics, 2009, 56(11): 4483-4491.

[7] Dannehl J, Wessels C, Fuchs F W. Limitations of voltage-oriented PI current control of grid-connected pwm rectifiers with filters[J]. IEEE Transactions on Industrial Electronics, 2009, 56(2): 380-388.

[8] Yin Jinjun, Duan Shanxu, Liu Bangyin. Stability analysis of grid-connected inverter with LCL filter adopting a digital single-loop controller with inherent damping characteristic[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2): 1104-1112.

[9] Malinowski M, Bernet S. A simple voltage sensorless active damping scheme for three-phase PWM converters with an LCL filter[J]. IEEE Transactions on Industrial Electronics, 2008, 55(4): 1876-1880.

[10] 李芬, 邹旭东, 邹云屏, 等. 并网LCL滤波的PWM整流器输入阻抗分析[J]. 电工技术学报, 2010, 25(1): 97-103.

Li Fen, Zou Xudong, Zou Yunping, et al. Input impedance analysis of LCL-filter PWM rectifier connected to grid[J]. Transactions of China Electrotechnical Society, 2010, 25(1): 97-103.

[11] Cheng Daizhan, Hu Xiaoming, Shen Tielong. Analysis and design of nonlinear control systems[M]. Heidelberg: Science Press & Springer, 2010: 279-306.

[12] 乐江源, 谢运祥, 张志, 等. 三相有源电力滤波器精确反馈线性化空间矢量PWM复合控制[J]. 中国电机工程学报, 2010, 30(15): 32-39.

Le Jiangyuan, Xie Yunxiang, Zhang Zhi, et al. Space vector PWM control of three-phase active power filter using exact feedback linearization[J]. Proceedings of the CSEE, 2010, 30(15): 32-39.

[13] Kim D E, Lee D C. Feedback linearization control of three-phase UPS inverter systems[J]. IEEE Transactions on Industrial Electronics，2012，57（3）： 963-968.

[14] Xia Changliang, Geng Qiang, Gu Xin, et al. Inputoutput feedback linearization and speed control of a surface permanent-magnet synchronous wind generator with the boost-chopper converter[J]. IEEE Transactions on Industrial Electronics, 2012, 59(9): 3489-3500.

[15] Mahmud M A, Pota H R,Hossain M J, et al. Robust partial feedback linearizing stabilization scheme for three-phase grid-connected photovoltaic systems[J]. IEEE Journal of Photovoltaics, 2014, 4(1): 423-431.

[16] Sehirli E, Altinay M. Input-output linearization control of three-phase voltage source PWM rectifier using L and LCL filter[C]. 45th International Universities Power Engineering Conference, Wales, UK, 2010: 1-6.

[17] Kim D, Lee D. Feedback linearization control of three-phase AC/DC PWM converters with LCL input filters[C]. 7th International Conference on Power Electronics, Daegu, Korea: EXCO, 2007: 766-771.

[18] 张兴, 张崇巍. PWM整流及其控制[M]. 北京: 机械工业出版社, 2011.

Nonlinear Damping Controller for Grid-Connected LCL Filters

Yang RenzengZhang Guangxian
（Shandong UniversityJinan250061China）

This paper presents a cascading nonlinear controller that applies to the grid-connected converter with LCL filters, based on linearization control. Herein, on the basis of an affine nonlinear model of three-phase grid-connected converter with LCL filter, the active and reactive currents of the converter at grid side and converter side are controlled with global linearization, through decoupling exaction from nonlinear feedback linearization controller. Consequently, the active damping of the filter is obtained. The cascading nonlinear controller removes the resonance of LCL filters and promotes the control performance of the converter effectively. Simulation and experimental results show the validation and feasibility of the proposed strategy.

Grid-connected LCL filter, active damping, nonlinear controller, feedback linearization

TN713

杨仁增男，1971年生，博士，工程师，研究方向为光伏并网逆变器及其电能质量控制。

张光先男，1965年生，博士，研究员，博士生导师，研究方向为电力电子与电力传动、特种电源技术。

国家自然科学基金资助项目（51207083、61471372）。

2014-02-25改稿日期 2014-04-08