基于功率变化子空间的直接功率控制

周小杰　张　霞　汪　飞

（1. 安徽理工大学电气与信息工程学院　淮南　232001

2. 上海大学机电工程与自动化学院　上海　200072）

基于功率变化子空间的直接功率控制

周小杰1，2张霞2汪飞2

（1. 安徽理工大学电气与信息工程学院淮南232001

2. 上海大学机电工程与自动化学院上海200072）

根据瞬时功率理论，建立三相电压型并网逆变器的功率数学模型，考虑了瞬时功率对功率变化率产生的交叉耦合影响，推导出维持瞬时功率不变的平衡矢量的表达式，建立功率变化子空间，在子空间中研究逆变器输出电压空间矢量对瞬时功率的作用，分析传统方法矢量选择的不足之处。在此基础上，提出一种基于功率变化子空间的直接功率控制方法。该方法通过设定有功功率和无功功率优先级别，建立开关表，更准确地选择了电压空间矢量，使得并网逆变器拥有更宽的功率调节范围，减小了功率脉动。最后通过仿真与实验对两种不同的方法进行对比，验证了该方法的可行性和正确性。

并网逆变器功率变化子空间交叉耦合直接功率控制开关表

0　引言

面对能源危机与环境危机，国内外越来越重视发展可再生能源，新能源发电进入电力系统的规模应用，对于缓解能源紧张和抑制环境污染起到非常积极的作用。各种可再生能源，如太阳能、风能，通常都需要使用逆变器实现并网以满足电网对电能质量的要求，于是并网逆变器控制技术在并网发电系统中已成为关键性技术［1-5］。三相电压型并网逆变器被广泛地应用于各个领域，并网逆变器直接功率控制（Direct Power Control，DPC）因其结构简单，功率因数可调，动态响应快等优点，得到了国内外学者持续不断的研究［6-9］。

直接功率控制通过开关表选择合适的逆变器输出电压矢量直接对系统的功率进行调节，具有优越的功率控制性能。文献［10］提出的直接功率扇区划分方法和开关表具有深远的影响，大多数文献所提及的直接功率控制策略都是由此改进而来。文献［11］提出了一种交替采用有功功率开关表和无功功率开关表的双开关表控制策略，可提高系统的动、静性能。文献［12］采用12扇区划分，优化了传统开关表，加强了对无功功率的控制能力。文献［13］采用非对称的滞环控制器减小有功功率的稳态误差。文献［14］将整个空间重新划分为18个扇区，提出一种新的具有通用性的开关表，并论述了其原理。但是，上述文献仅利用电网电压或虚拟磁链在空间矢量图中进行分析，在选择电压空间矢量时，忽略了瞬时功率对功率变化率产生的交叉耦合影响，使得矢量选择存在误差。

本文以瞬时功率理论为基础推导三相电压型并网逆变器瞬时功率数学模型，计算得到维持瞬时功率不变的平衡矢量，建立基于功率变化的子空间，分析逆变器输出基本电压空间矢量对有功功率和无功功率变化率的影响，设定有功功率和无功功率变化的优先级别，从而建立开关表，使得电压空间矢量选择更为准确，系统获得了更宽的功率可调范围，减小了功率脉动。通过仿真和实验的详细对比分析，验证了该方法的可行性和正确性。

1　并网逆变器功率模型和功率变化子空间

1.1并网逆变器功率模型

三相电压型并网逆变器电路结构如图1所示。图中，ea、eb和ec分别为三相电网的相电压；ia、ib和ic分别为逆变器的三相输出电流（参考方向如图1所示）；ua、ub和uc为逆变器交流侧输出电压，逆变器通过电感L接到三相电网上。

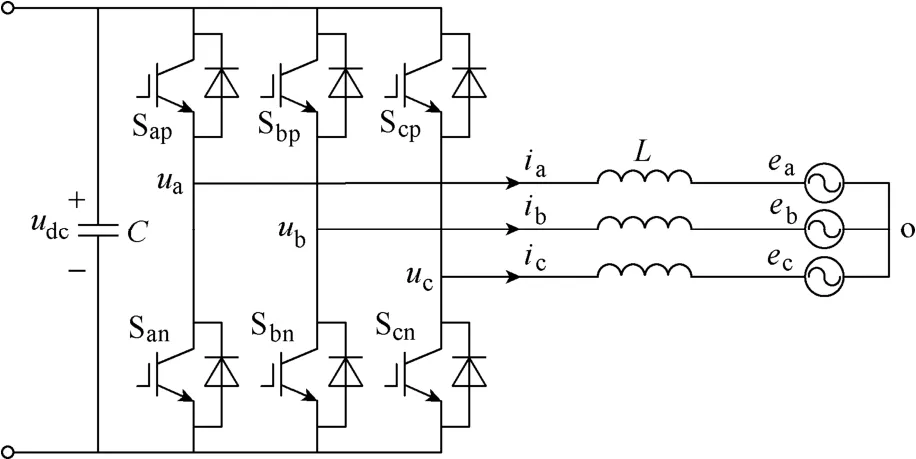
图1　三相电压型并网逆变器Fig.1　Diagram of three phase voltage grid-connected inverter

逆变器的八个开关状态在空间上形成了八个基本电压空间矢量，如图2所示。

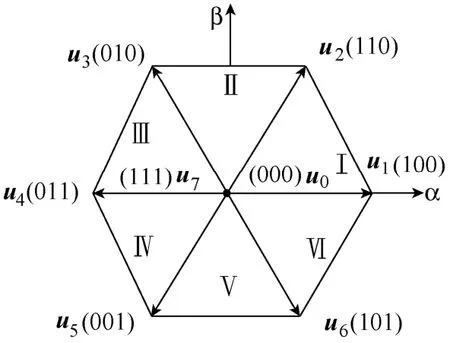
图2　电压空间矢量Fig.2　Space vectors of three phase voltage

根据基尔霍夫定律可得如下关系

定义3/2变换矩阵C3/2为

式中，xαβ=（xα, xβ）T；xabc=（xa，xb，xc）T。xα、xβ为xa、xb、xc在αβ坐标系下的α分量和β分量。

式（1）经3/2变换后，可得

根据瞬时功率理论［15］计算有功功率p和无功功率q如下

对p、q求导，可得

考虑电网电压为三相平衡电压

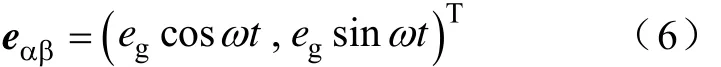
式中，eg为三相电网电压在两相坐标系下的合成矢量幅值；ω为电网电压角频率，则有

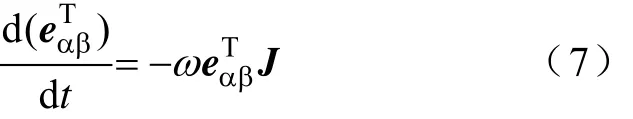
将式（3）、式（7）代入式（5），整理得到

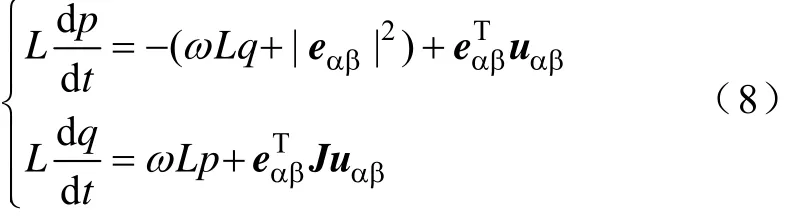
1.2功率变化子空间划分

令dp/dt=0，由式（8）可得

令dq/dt=0，同理可得

当dp/dt=0且dq/dt=0时，解得

记同时满足dp/dt=0且dq/dt=0的矢量为平衡矢量ueqαβ，则有

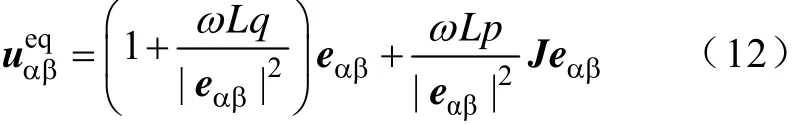
在平面内，以矢量ueqαβ末端为原点，定义dp/dt轴和dq/dt轴，dp/dt轴平行于eαβ，与eαβ方向一致，dq/dt轴平行于Jeαβ，与Jeαβ方向相反（电压矢量在Jeαβ上投影越大，无功变化率越小）。某一时刻下的功率变化子空间划分如图3所示，dp/dt轴和dq/dt轴将平面划分为四个子空间，每个子空间对应dp/dt和dq/dt的符号唯一。

图3　功率变化子空间Fig.3　Subspace for power variation

2　基于功率变化子空间的直接功率控制

2.1电压空间矢量作用分析

由图3可知，某一时刻，逆变器输出dp/dt和 dq/dt的符号取决于逆变器输出电压矢量的un的末端落在哪一个子空间。例如，当逆变器输出电压矢量为u1时，dp/dt＞0，dq/dt＞0；当逆变器输出电压矢量为u3时，dp/dt＜0，dq/dt＜0。逆变器输出电压矢量对有功功率p和无功功率q的调节能力不同，随电网电压矢量和瞬时功率的大小和方向发生变化，逆变器输出电压空间矢量越靠近dp/dt轴正方向，有功功率增加趋势越明显，越靠近dp/dt轴负方向，有功功率减小趋势越明显，无功功率分析同理。

传统的直接功率控制方法忽略了瞬时功率对功率变化率产生的交叉耦合影响，等价为本方案中的平衡矢量为电网电压矢量，若在传统方案中定义dp/dt轴，则如图3虚线所示，由此可以看出传统方案中存在一些问题，归纳如下：

（1）由式（12）知，当有功功率非零时，ueqαβ与eαβ不重合，当电网电压角度θg接近逆变器基本输出电压空间矢量角度（记作θn）时，有功功率的大小决定了dp/dt轴与矢量eαβ的相对位置，有功功率的绝对值越大，平衡矢量ueqαβ的幅值越大，ueqαβ与eαβ的夹角就越大，传统方法错误选择矢量的几率就越高。如电网电压逆时针旋转时，当θg接近θn但小于θn时，有功功率大小直接影响到un对瞬时功率的作用方向，θg接近θn且大于θn时，有功功率大小直接影响到un+3对瞬时功率的作用方向。

（2）如图3所示，当q较小时，增大有功功率的矢量会增多（即末端落入A、D子空间的矢量会增多），那么传统控制策略中选择减小p的矢量，实际上可能会使p增加，选择矢量出现错误。当q特别小时，错误选择电压空间矢量的几率将会大大增加（如：1+ωLq/|eαβ|2＜0）。

传统的直接功率控制策略选择矢量会发生错误，当瞬时功率较大时，选择矢量发生错误的几率也会增加。本文考虑了瞬时功率对功率变化率带来的交叉耦合影响，使得矢量选择更为准确。

2.2控制策略分析

当逆变器输出矢量等于平衡矢量ueqαβ时，其输出功率将保持不变，由式（12）可知，平衡矢量的旋转速度与电网电压合成矢量的旋转速度相同，两者的相对位置保持不变。当逆变器输出电压矢量等于平衡矢量ueqαβ时，逆变器输出功率将保持不变。由式（8）可以看出，功率的变化不唯一由电网电压决定，传统方法仅通过电网角度所在的扇区去选择逆变器输出电压矢量，因此其不能保证功率按期望变化。

在图3的基础上，作六边形的外接圆交dp/dt、dq/dt两轴分别于p+点、p-点、q+点和q-点，记Op+、Op-、Oq+和Oq-与电网电压矢量eαβ的夹角分别为φp+、φp-、φq-和φq+，如图4所示。

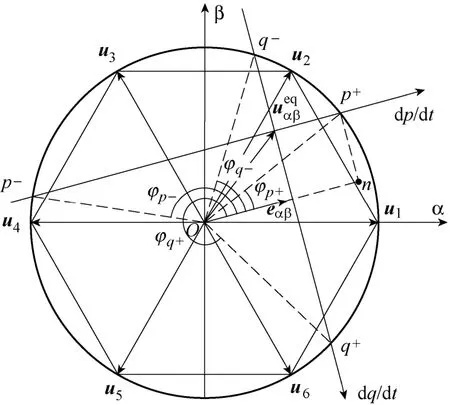
图4　基于子空间划分的矢量分析Fig.4　Illustration of vector based on subspaces

分析图4知，Op+、Op-、Oq+和Oq-在空间位置上越接近ueqαβ，对应增加p、减小p、增加q和减小q的可选矢量越少且作用越弱。定义p+、p-、q+和q-优先级，规则如下：记ueqαβ与eαβ间的角度为θ0，与θ0间的夹角最小时，相应的p+、p-、q+和q-设定为优先级，分别表示选择电压空间矢量时优先考虑增加p、减小p和增加q、减小q。图4中，过点p+，作p+n交p轴的平行线On于点n，由式（12）可知，，图4中外接圆半径长度为为直流母线电压），计算如下

同理可得φp-、φq-和φq+的三角函数值

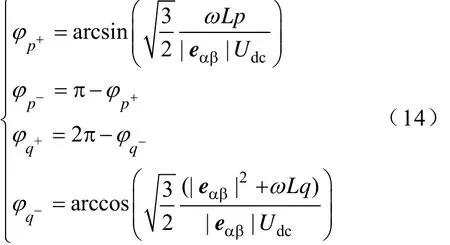
有功功率和无功功率的控制采用滞环控制，瞬时功率与给定值比较，得到Sp和Sq，其值为1时表示功率需要增加，为0时表示功率需要减少。由上述分析得到开关表见表1。其中sec（p+）、sec（p-）、sec（q+）、sec（q-）分别为p+、p-、q+和q-所在扇区号。p+、p-、q+和q-表示确定的优先级。

表1　开关表Tab.1　Dynamic switching table

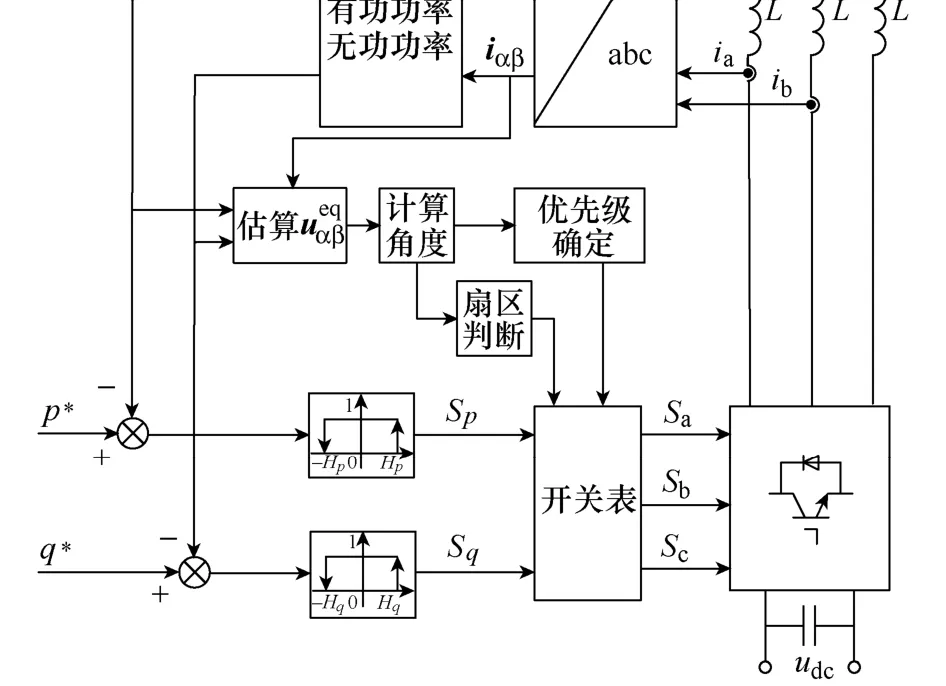
图5　基于功率变化子空间的直接功率控制系统框图Fig.5　Block diagram of DPC based on subspace of power variation

3　仿真与实验

3.1仿真研究

在Matlab/Simulink仿真平台上对系统进行仿真测试，仿真参数设置见表2。

表2　系统参数Tab.2　Parameters for the system

文献［14］在介绍了直接功率控制的调制机制的基础上提出了一种通用开关表，并与传统开关表［10］和优化后的开关表［12］进行了比较，得出其提出的直接功率控制方案的瞬时功率控制效果最好。将文献［14］提出的方法记为A1，本文提出的方法记为A2。

图6、图7分别为使用A1、A2两种方法情况下的系统稳态运行仿真结果，有功功率给定p*=1 200W，无功功率给定q*=0。可以看出，使用两种方法时，有功功率误差大致相同，为1 120～1 250W；无功功率误差有明显区别，使用A1时，无功功率为-70～120var，使用A2时，无功功率为-70～90var。使用A1时，电流总谐波畸变率为3.94%，使用A2时，电流总谐波畸变率为3.12%。结果表明，A2较A1稳态性能好。

图6　系统稳态运行仿真结果（A1）Fig.6　Simulation results of the system under steady-state operation （A1）

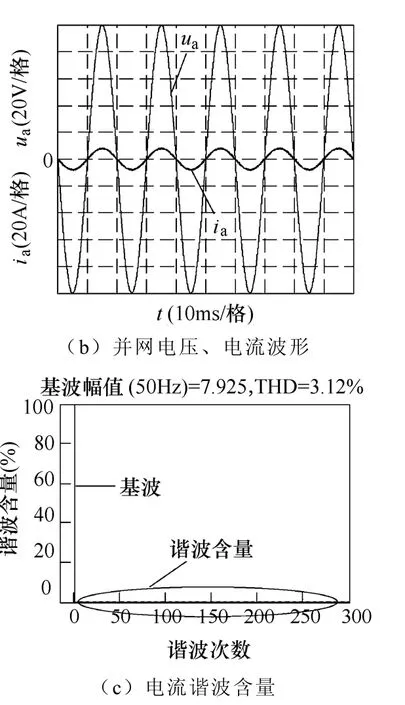
图7　系统稳态运行仿真结果（A2）Fig.7　Simulation results of the system under steady-state operation （A2）

图8为使用本文提出的方法，当电网相电压峰值由100V跌落为80V时的仿真结果，有功功率给定p*=1 200W，无功功率给定q*=0。从仿真结果可以看出，本文提出的方法在电网电压波动较大时，功率仍然具有良好的动态响应。

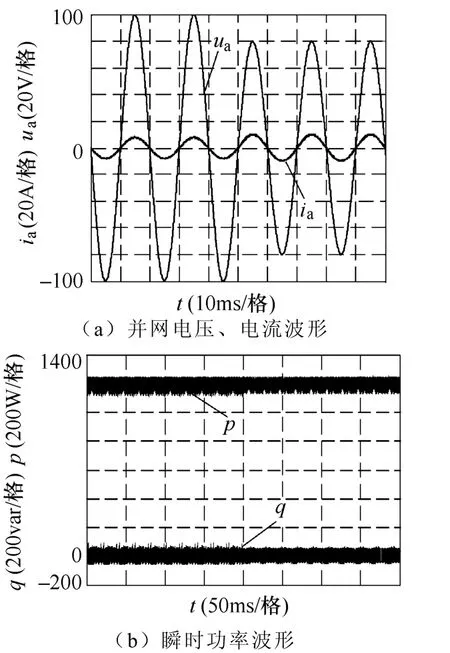
图8　电网电压波动时仿真结果（A2）Fig.8　Simulation results of the grid voltage fluctuation （A2）

图9、图10分别为使用两种方法时，系统功率给定突变的仿真运行结果。当t=0.1s时，有功给定由1 000W突变到4 000W。使用A1时，有功突变瞬间，无功功率出现尖峰，峰值约500var，如图9a所示，使用A2时，没有此尖峰，如图10a所示。

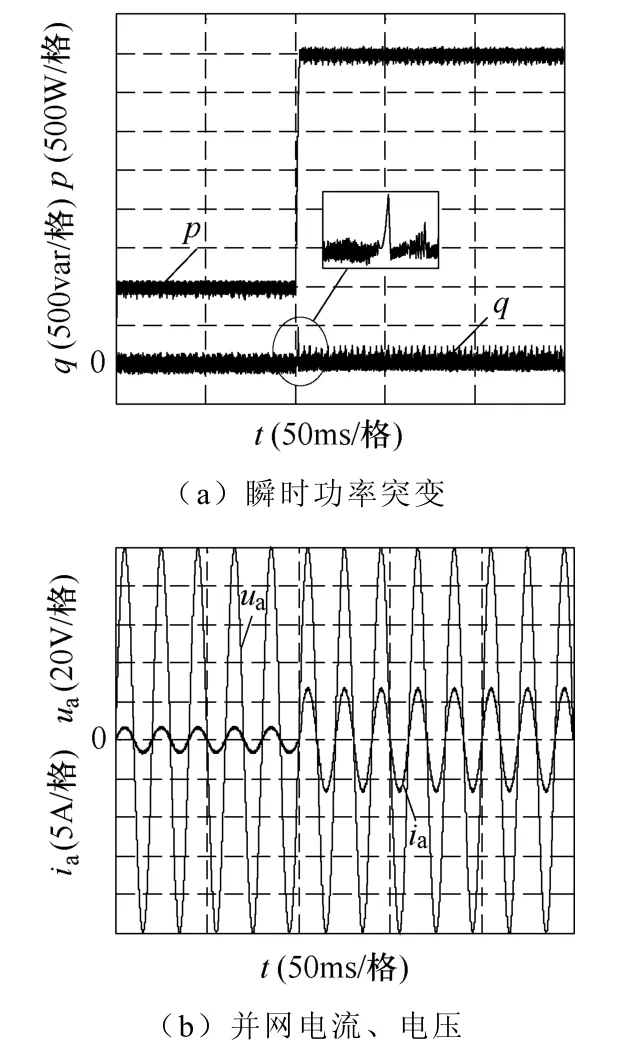
图9　功率给定突变仿真运行结果（A1）Fig.9　Simulation results during step power reference application（A1）

图10　功率给定突变仿真运行结果（A2）Fig.10　Simulation results during step power reference application（A2）

当有功功率给定为4 000W，无功功率给定为0时，将有功功率和无功功率与并网电流放在同一坐标系下进行观察，如图11所示。可见，当θg接近θn时，使用A1时的瞬时功率脉动明显较使用A2时的大，与上述理论分析一致。

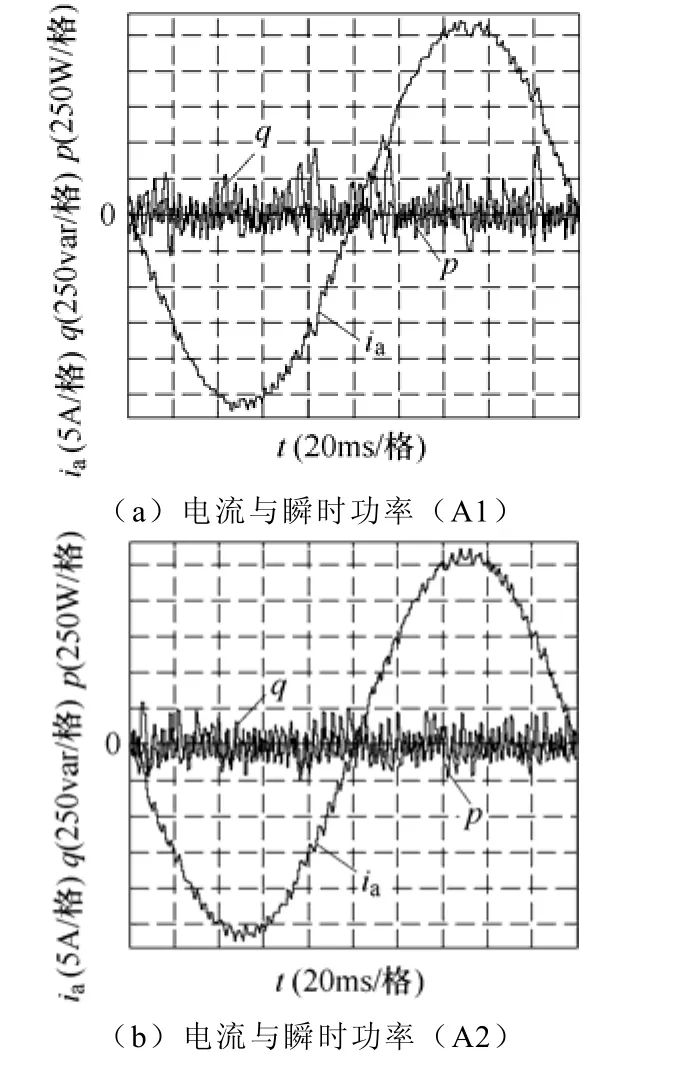
图11　并网电流与瞬时功率关系Fig.11　Relationship between current and instantaneous power

当有功功率给定为9 000W，无功功率给定为-5 000var，仿真运行结果如图12、图13所示。可以看出，使用A1，系统不能稳定，瞬时功率出现振荡，并网电流畸变大，使用A2，系统依然能够稳定，并网电流波形正弦度良好，由此可见，方法A2较A1使系统拥有更宽的功率调节范围。

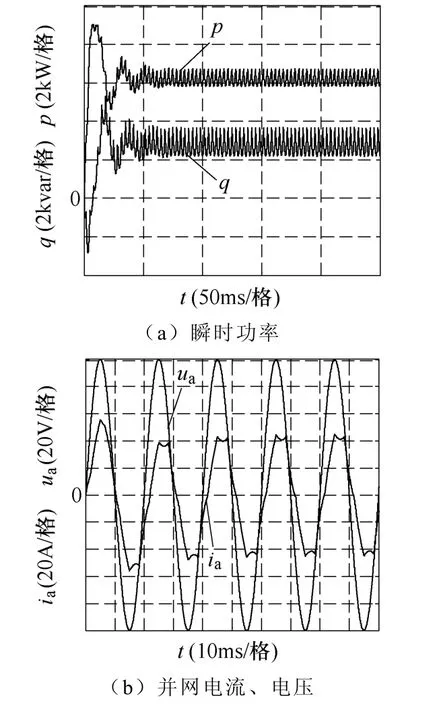
图12　输出大功率时的仿真运行结果（A1）Fig.12　Simulation results during high power output （A1）

图13　输出大功率时的仿真运行结果（A2）Fig.13　Simulation results during high power output （A2）

从仿真结果可知，方法A2较A1使系统拥有更好的稳态性能，具有更宽的功率调节范围。

3.2实验研究

为验证控制策略，搭建了一个额定功率为1kW的三相并网逆变器系统实验平台，系统控制策略的软件实现由英飞凌公司的XC2785微控制器完成，D-A芯片采用DAC8565，有功功率和无功功率通过CAN通信由上位机给定，实验系统的参数和仿真系统参数相同。

图14为系统分别使用A1和A2稳态运行时交流侧a相电压、电流波形和电流频谱分析图。可以看出，电流与电网电压相位一致，正弦度良好，A2较A1，电流波形更加平滑，总谐波畸变率（Total Harmonic Distortion，THD）也有明显改善。

图14　稳态运行实验波形及频谱分析Fig.14　Experiment waveforms and spectrum analysis of steady state

图15为采用本文提出的方法，有功给定为1 000W（1（pu）），无功给定为0，当电网电压突减时的实验结果，从波形可以看出，功率的响应仍然保持不变，系统具有较强的鲁棒性。

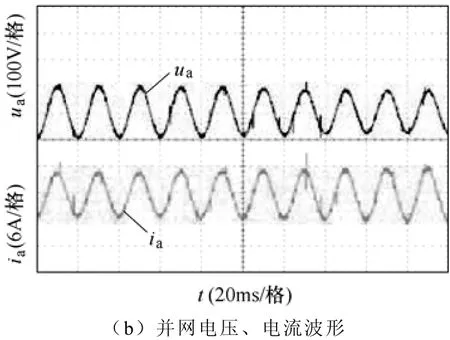
图15　电网电压波动实验波形（A2）Fig.15　Experiment waveforms of the grid voltage fluctuation （A2）

图16和图17分别为系统采用A1、A2时的动态响应实验结果，有功给定为1 000W（1（pu）），无功给定由0突变到200var（0.2（pu））。可见，两种控制策略都能实现对功率的快速跟踪。

有功功率给定为1 300W（1.3（pu）），无功给定为-100var（-0.1（pu）），实验波形分别如图18、图19所示。可见，功率较大时，采用A1，功率脉动较大，采用A2，功率脉动较小。

图16　动态响应实验波形（A1）Fig.16　Dynamic response experiment waveforms （A1）

图17　动态响应实验波形 （A2）Fig.17　Dynamic response experiment waveforms （A2）

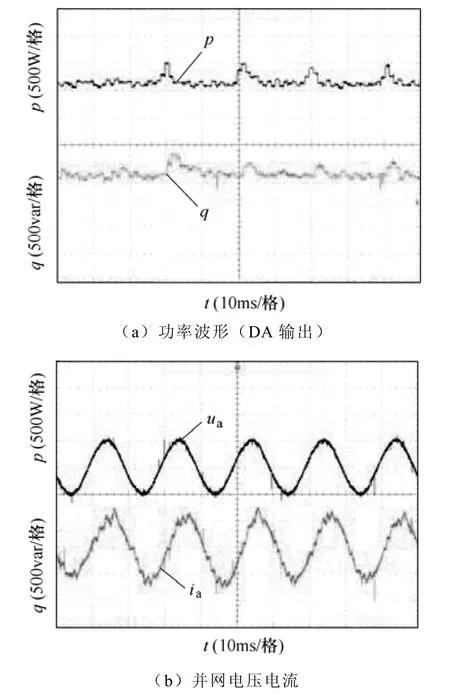
图18　较大功率下的实验波形 （A1）Fig.18　Experiment waveforms during high power reference application （A1）

采用传统方法，当并网逆变器输出有功功率小于或等于额定功率时，错误选择矢量的几率较小，从波形上看即功率脉动小；当并网逆变器输出有功功率大于额定功率时，根据前面的分析可知错误选择矢量的几率变大，造成功率脉动变大。实验结果表明，A2较A1使系统拥有更好的控制性能，虽然动态性能没有A1优势明显，但稳态性能得到提高，具有更宽的功率调节范围。

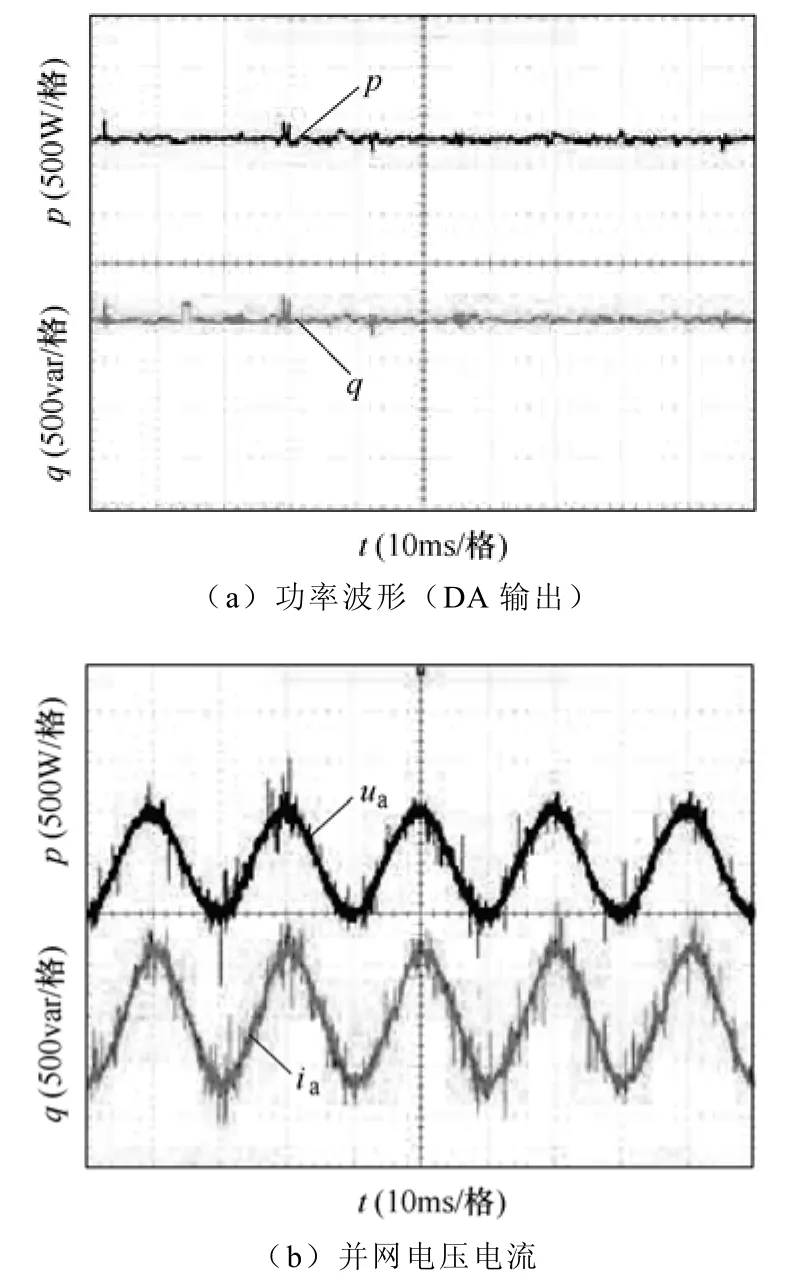
图19　较大功率下的实验波形 （A2）Fig.19　Experiment waveforms during high power reference application （A2）

4　结论

仿真和实验的结果表明，方法A2较A1使系统拥有更好的稳态性能，具有更宽的功率调节范围。这是因为方法A1忽略了瞬时功率对功率变化率产生的交叉耦合影响，当电网电压角度接近逆变器基本输出电压空间矢量角度或瞬时功率较大时，电压空间矢量选择易存在错误，方法A2考虑了瞬时功率对功率变化率带来的交叉耦合影响后，电压空间矢量的选择更准确。

直接功率控制是一种结构简单、响应快速的控制策略，本文通过详细的仿真和实验对比分析，证明了提出的控制策略的可行性和正确性，该策略使系统具有更好的控制性能、更宽的功率调节范围。

［1］ 赵方平，杨勇，阮毅，等. 三相并网逆变器直接功率控制和直接功率预测控制的对比［J］. 电工技术学报，2012，27（7）： 212-220.

Zhao Fangping，Yang Yong，Ruan Yi，et al. Comparative study for direct power control and direct power predictive control in three-phase grid-connected inverters［J］. Transactions of China Electrotechnical Society，2012，27（7）： 212-220.

［2］ 杨勇，赵方平，阮毅，等. 三相并网逆变器模型电流预测控制技术［J］. 电工技术学报，2011，26（6）：153-159.

Yang Yong，Zhao Fangping，Ruan Yi，et al. Model current predictive control for three-phase grid-connected inverters［J］. Transactions of China Electrotechnical Society，2011，26（6）： 153-159.

［3］ 赵梅花，阮毅，杨勇，等. 直驱式混合励磁风力发电系统控制策略的研究［J］. 电力系统保护与控制，2010，38（12）： 19-23.

Zhao Meihua，Ruan Yi，Yang Yong，et al. Control strategy study on direct-driven type hybrid excitation wind power system［J］. Power System Protection and Control，2010，38（12）： 19-23.

［4］ 曾正，赵荣祥，杨欢，等. 多功能并网逆变器及其在微电网电能质量定制中的应用［J］. 电网技术，2012，36（5）： 58-67.

Zeng Zheng，Zhao Rongxiang，Yang Huan，et al. A multi-functional grid-connected inverter and its application to customized power quality of microgrid［J］. Power System Technology，2012，36（5）： 58-67.

［5］ 章玮，王宏胜，任远，等. 不对称电网电压条件下三相并网型逆变器的控制［J］. 电工技术学报，2010，25（12）： 103-110.

Zhang Wei，Wang Hongsheng，Ren Yuan，et al. Investigation on control of three-phase grid-connected inverters under unbalanced grid voltage conditions［J］. Transactions of China Electrotechnical Society，2010，25（12）： 103-110.

［6］ Zhi D，Xu L，Williams B W. Improved direct power control of grid-connected DC/AC converters［J］. IEEE Transactions on Power Electronics，2009，24（5）： 1280-1292.

［7］ Restrepo J A，Aller J M，Viola J C，et al. Optimum space vector computation technique for direct power control［J］. IEEE Transactions on Power Electronics，2009，24（6）： 1637-1645.

［8］ 李子欣，李耀华，王平，等. PWM 整流器在静止坐标系下的准直接功率控制［J］. 中国电机工程学报，2010，30（9）： 47-54.

Li Zixin，Li Yaohua，Wang Ping，et al. Novel quasi direct power control method for PWM rectifier in stationary frame［J］. Proceedings of the CSEE，2010，30（9）： 47-54.

［9］ 杨兴武，赵剑飞，杨兴华，等. 基于变换器输出电压快速计算的直接功率控制方法［J］. 中国电机工程学报，2010，30（36）： 59-64.

Yang Xingwu，Zhao Jianfei，Yang Xinghua，et al. Direct power control based on output voltage computation technique for AC/DC converters［J］. Proceedings of the CSEE，2010，30（36）： 59-64.

［10］ Noguchi T，Tomiki H，Kondo S，et al. Direct power control of PWM converter without power-source voltage sensors［J］. IEEE Transactions on Industry Applications，1998，34（3）： 473-479.

［11］ 王久和，李华德. 一种新的电压型 PWM 整流器直接功率控制策略［J］. 中国电机工程学报，2005，25（16）： 47-52.

Wang Jiuhe，Li Huade. A novel control strategy for photovoltaic grid-connected inverter［J］. Proceedings of the CSEE，2005，25（16）： 47-52.

［12］ 郭文勇，赵彩宏，张志丰，等. 电压型超导储能系统的统一直接功率控制方法［J］. 电网技术，2007，31（9）： 58-63. Guo Wenyong，Zhao Caihong，Zhang Zhifeng，et al. A unified direct power control method for voltage type superconducting magnetic energy storage system［J］. Power System Technology，2007，31（9）：58-63.

［13］ Hu Jiabing，Zhu Z Q. Investigation on switching patterns of direct power control strategies for gridconnected DC-AC converters based on power variation rates［J］. IEEE Transactions on Power Electronics，2011，26（12）： 3582-3598.

［14］ 陈伟，邹旭东，唐健，等. 三相电压型 PWM 整流器直接功率控制调制机制［J］. 中国电机工程学报，2010，30（3）： 35-41.

Chen Wei，Zou Xudong，Tang Jian，et al. DPC modulation mechanism of three-phase voltage source PWM rectifiers［J］. Proceedings of the CSEE，2010，30（3）：35-41.

［15］ Superti-Furga G，Todeschini G. Discussion on instantaneous p-q strategies for control of active filters［J］. IEEE Transactions on Power Electronics，2008，23（4）：1945-1955.

Direct Power Control Based on Subspace of Power Variation

Zhou Xiaojie1，2Zhang Xia2Wang Fei2
（1. Anhui University of Science and TechnologyHuainan232001China
2. Shanghai UniversityShanghai200072China）

The instantaneous power mathematical model of three-phase voltage-source inverter was established based on instantaneous power theory. Considering the instantaneous power for power rate of cross-coupling effect，the equilibrium vector was derived and the subspace of power variation was established. Then the effect of voltage space vector on instantaneous power in the subspace was studied，compared with the traditional switching tables. A new direct power control strategy based on subspace of power variation was proposed，which built a dynamic switching table by setting active and reactive power priority reference. The proposed strategy can select the voltage space vector more accurately，broaden the power adjustment range of inverter，and reduce the power ripple. The proposed control strategy was verified by the simulation and experiment.

Grid-connected inverter，power variation subspace，cross-coupling，direct power control，switching table

TM464

周小杰男，1979年生，博士研究生，讲师，研究方向为新能源并网发电。

张霞女，1986年生，硕士研究生，研究方向为电力电子与电力传动。

国家自然科学青年基金项目（51107078）和台达环境与教育基金会《电力电子科教发展计划》项目（DREG2012006）资助。

2013-12-07改稿日期 2014-06-23