电力电子系统阻抗测量的分段二叉树法

岳小龙　卓　放　张政华　师洪涛　张　东

（西安交通大学电气工程学院　西安　710049）

电力电子系统阻抗测量的分段二叉树法

岳小龙卓放张政华师洪涛张东

（西安交通大学电气工程学院西安710049）

在分析和设计包含电力电子变换器的系统时，由于阻抗和系统稳定性之间的密切关系，阻抗测量就显得十分重要。传统的扫频法采用等频率间隔的方式注入扰动信号并测量电力电子系统阻抗，由于不能在测量结果和测量过程之间建立起有效的联系，因此是一种低准确性、低效率和低可靠性的开环测量方法。通过建立阻抗测量结果准确度和测量频率间隔之间的数学关系，提出了一种分段二叉树阻抗测量方法。使用该方法，可以根据结果的准确度要求自动地确定测量频率点的位置，与传统的扫频法相比，本文提出的方法可以更加准确和有效地测量电力电子系统阻抗。单相交流系统和三相交流系统的阻抗测量结果证明了提出的方法的有效性。

电力电子系统阻抗测量频率扫描二叉树误差校验

0　引言

电力电子变换器的恒功率特性会导致系统因为负阻抗而不稳定［1-14］，因此，在包含电力电子变换器的系统设计中，小信号稳定性分析就显得非常重要。一种常见的方法是建立系统的小信号模型，通过零极点来分析系统的稳定性。但是，在实际应用中，建模需要的参数很难准确获取，因而限制了这种方法的使用。自从1976年R. D. Middlebrook第一次提出系统稳定性和输入、输出阻抗之间的关系［2］，基于阻抗的稳定性判据开始获得广泛的应用。尤其是当系统的各部分组件由不同制造商提供时，阻抗稳定性判据显得更加方便，因为测量输入、输出阻抗比建立小信号模型容易的多。基于上述原因，在诸多应用场合，阻抗测量技术显得越来越重要［9-16］。

由于电力电子变换器的开关非线性，在电力电子系统阻抗测量中，基于一系列正弦扰动信号注入的方法是最常用的方法［4-14］。为了获取所需频率范围内的阻抗，该方法要求注入适当功率的一系列不同频率的电压或电流扰动信号，常见的注入装置包括功率放大器、网络分析仪和斩波电路等［4-14］。直流系统中，在特定频率处注入扰动信号，通过测量和数据处理即可获得该频率点处的阻抗［4-8］。三相交流系统中，一般考虑在dq坐标系下的阻抗，需要两次线性独立的扰动信号注入才能获取某一特定频率处的阻抗矩阵［9-13］。实际电力电子系统中，阻抗特性是连续的，但测量得到的只是阻抗的离散数据点，所以选择合适的测量频率点对阻抗测量的准确性和效率有很大的影响［16］。

扫频法是目前常用的确定注入扰动信号频率点的方法，具体做法就是等间隔地从测量起点到终点依次注入扰动信号［4-13］。如果待测网络的阻抗特性变化平缓，比如只包含电阻和电感的负载网络，较大的测量频率间隔即可得到准确的测量结果；如果待测网络的阻抗特性包含多次谐振，比如含有大量电感和电容支路的网络，需要使用较小的测量频率间隔才能获取准确的结果［16］。然而，在测量之前，由于不知道阻抗的特性，使得扫频法中频率间隔的选择变得很困难，过大的频率间隔会导致测量结果不准确，过小的频率间隔会造成测量时间的浪费，目前还没有有效的方法来解决这个问题。

为此，本文提出了一种适用于电力电子系统阻抗测量的分段二叉树方法。该方法中，注入扰动信号的频率间隔可以根据待测网络的阻抗特性和给定的测量结果准确性要求自动选取。相对于传统的扫频法，本文提出的阻抗测量方法可以更加准确和高效地测量电力电子系统阻抗。

1　阻抗测量及其数学描述

在基于正弦扰动信号注入的阻抗测量中，注入电压或电流扰动都是可行的［4-14］。直流/单相交流系统扰动注入原理图如图1所示，其中并联结构表示电流注入，串联结构表示电压注入［5，6］。

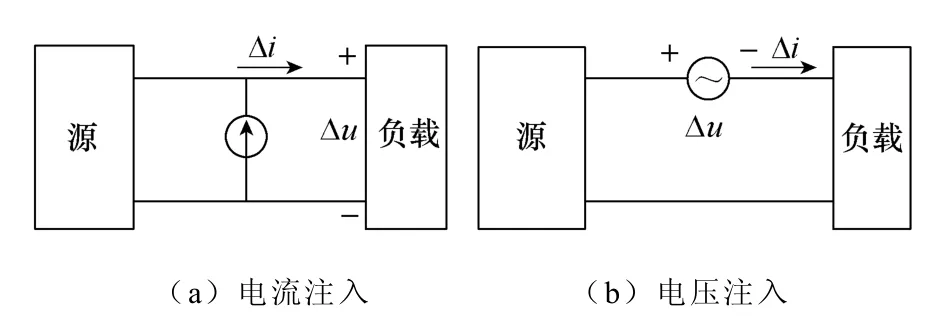
图1　直流/单相交流系统扰动信号注入示意图Fig.1　Injection diagram for DC/single-phase AC system

对于三相交流系统，可以采用三相对称的扰动注入方法。也可以采用注入两相扰动的不对称注入方法。以注入电流扰动为例，注入三相对称扰动电流的原理示意图如图2a所示，注入不对称电流扰动的原理示意图如图2b所示［9］。

图2　三相交流系统扰动信号注入示意图Fig.2　Injection diagram for three-phase AC system

对于直流系统，以图1a所示电流扰动注入为例，某一频率的电流信号在系统稳态工作时注入，通过测量和记录扰动电流Δi和扰动电压Δu，则该频率处的阻抗可以表示为

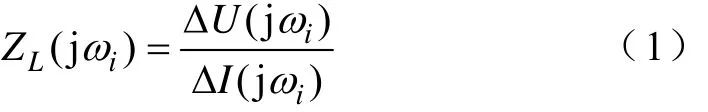
对于三相交流系统，可以在dq坐标系下获取类似于直流系统的稳态工作点。三相交流系统在dq坐标系下的阻抗可以表示为

由于式（2）中包含4个未知数Zdd、Zdq、Zqd和Zqq，需要注入两组线性独立的电流扰动信号。而如图2b所示的不对称注入方法对硬件要求更低，当采用不对称注入法时，注入的两组扰动信号的形式为［9］

式中，eω是系统的基波频率；sω是注入扰动信号在dq坐标系下的频率。

采用不同的iω和sω重复多次测量，即可得到需要的频率范围内的阻抗特性曲线。阻抗的幅值和相角可以表示为

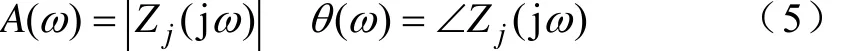
阻抗的实部和虚部可以表示为

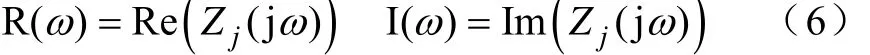
式中，Zj表示ZL、Zdd、Zdq、Zqd和Zqq，最终的阻抗特性曲线通过连接相邻两个数据点得到。

如果将真实的阻抗Z（ω）看做频率ω的函数，注入扰动信号相当于给定函数自变量ωi（i=0，1，…，n），阻抗测量结果相当于求函数值Z（ωi）。当阻抗测量结束，从式（5）可得一系列数据点A（ωi）和θ（ωi），连接相邻的数据点A（ωi）、A（ωi+1）和θ（ωi）、θ（ωi+1）即可得到幅频特性和相频特性。同理，根据式（6）可得阻抗的实部特性和虚部特性。

整个过程可以进一步抽象为如下数学过程：对于函数y=f（x），x∈［a，b］，选取数据点（xi，yi），其中i=1，2，…，n ，yi=f（xi）；并由此构成线性插值函数g（x），x∈［a，b］，yi=g（xi），如图3所示。数据点（xi，yi）即为通过测量得到的点，函数g（x）为阻抗测量结果。由此，阻抗测量可以转化为这样一个数学问题——选取一组数据点（xi，yi），使得由此构成的线性插值函数尽可能地接近原函数。问题的关键在于选择恰当的xi，其中i=0，1，…，n，对应到实际测量中，即注入正弦扰动信号频率ωi。

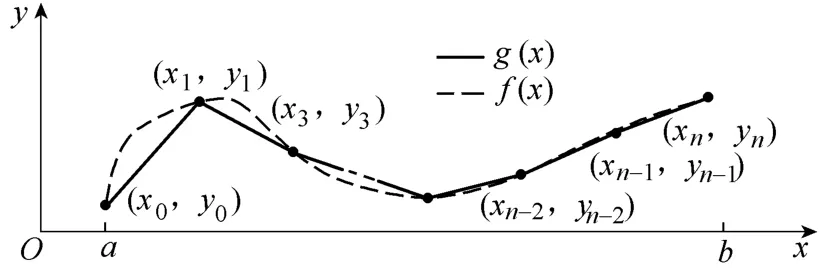
图3　阻抗测量的数学抽象和描述Fig.3　Mathematical description for impedance measurement

2　基于二叉树结构的阻抗测量方法

2.1传统的频率扫描方法

在传统的频率扫描方法中，正弦扰动信号采用等间隔的方式从测量起点到测量终点依次注入。从数学上讲，就是给定n+1个在测量区间［a，b］上等间隔分布的数据点xi（i=0，1，…，n），然后依次计算出对应的函数值yi=f（xi），这一过程如图4所示，其中粗实线表示已测量区间，细实线表示未测量区间。从图中可以看出，阻抗测量从低频到高频按照设定好的频率间隔依次进行，测量过程中，注入扰动信号与测量结果之间没有信息交换，因此，传统的频率扫描方法是一种开环的阻抗测量形式。

图4　扫频法的数学描述Fig.4　Description for frequency sweep method

频率扫描方法结构简单，然而，由于阻抗特性在测量完成前是未知的，因此，根据经验选取的测量频率间隔并不总是适合当前的待测网络。如果选取的频率间隔过大，可能导致阻抗测量结果不准确。如果选取的频率间隔过小，虽然可以得到准确的阻抗测量结果，但会浪费测量时间，减低效率。因此，传统的频率扫描方法是一种准确性差、效率和可靠性都很低的阻抗测量结构。

2.2频率间隔与测量结果准确性之间的关系

从数学上讲，阻抗测量就是寻找原函数f（x）的线性插值函数g（x）的过程。图5中，很明显地可以看出，使用的数据点越多，获取的测量结果越准确。如果能够建立测量结果和数据点之间的关系，那么阻抗测量就成为闭环系统，扫频法的测量频率间隔可以根据测量结果的准确性要求来确定。

图5　不同频率间隔对应的测量结果Fig.5　Measured results with different frequency interval

当g（x）≈f（x）时，图5中阴影部分的面积会非常小，反之亦然，当g（x）和f（x）构成的几何图形的面积非常小时，g（x）就是f（x）的一个很好的近似。假设xi（i=0，1，…，n）是在区间［a，b］上满足条件

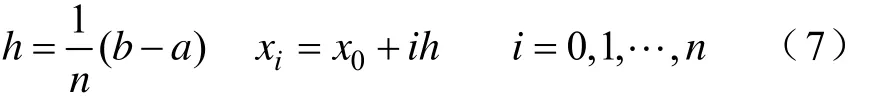
的n+1个数据点，其中h代表频率间隔，xi为注入扰动信号的频率。定义

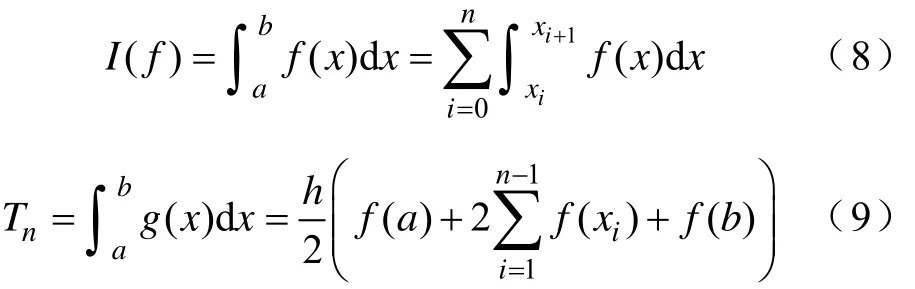
那么|（f）-Tn|就表示图5中阴影部分的面积。如果I（f）-Tn＜ε（ε为给定误差），那么g（x）≈f（x）。根据数值分析中有关数值积分的结论［17］

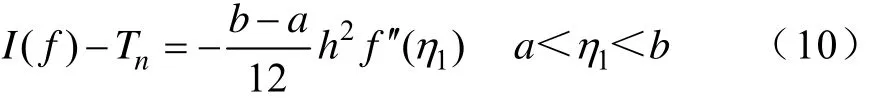
同理，当数据点增加到2n+1时

如果f″（x）在［a，b］上变化不大，即f′（η1）≈f″（η2），由式（10）和式（11），可得

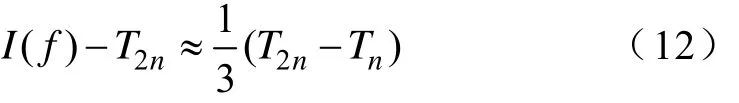
如果

那么|（f）-T2n|＜ε，也就是说，由2n+1个数据点构成的插值函数g（x）是原函数f（x）的一个很好近似，此时误差界ε对应的测量频率间隔为h2。

2.3基于二叉树结构阻抗测量方法

前面分析了传统的扫频法中，测量频率间隔和测量结果准确性之间的定量关系。根据式（7）和式（9），可得

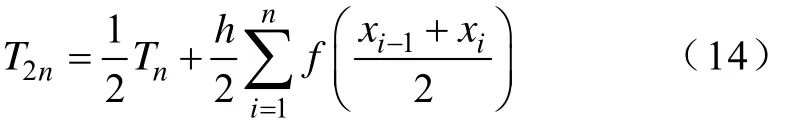
如果定义误差估计

由式（7）、式（13）～式（15）可以构造如图6所示的迭代过程。图6a中，圆圈中的数字代表区间对分次数j，图6b给出了迭代过程中测量数据点的分布情况。迭代的具体执行过程如下：首先取n=1，由式（7）计算h和xi，由式（9）计算Tn；然后取n=2，根据式（14）计算T2n。由Tn和T2n判断式（13）是否成立，如果成立，则迭代结束，根据获取的数据点画出阻抗特性曲线；如果式（13）不成立，则令Tn=T2n，n=3，根据式（14）计算T2n，重新判断式（13）是否成立。由于阻抗是复数，因此在计算Tn和T2n时，需要按照式（5）或式（6）将测量得到的阻抗数值写成幅值和相角或实部和虚部的形式，分别计算并按照式（13）判断误差是否满足条件。

图6　基于二叉树的阻抗测量结构Fig.6　Structure based on binary tree method

重复上述过程直到测量结果满足给定的误差要求。由于在测量过程中每一次增加n，都会使数据点和子区间数目加倍，类似于计算机程序设计中的二叉树结构，所以称这种方法为电力电子系统阻抗测量的二叉树结构［18］。

2.4分频段二叉树结构的阻抗测量方法

实际的电力电子系统阻抗，一般都是在部分区间阻抗特性曲线变化比较剧烈（比如包含多个谐振点）；而在其他区间变化趋势较为平坦（比如以阻感负载为主）。如果在整个待测区间都使用这种基于二叉树结构的阻抗测量方法，最终选取的频率间隔对于阻抗变化较为平缓的区间来说是一种浪费。

为了减小这种浪费，可以将待测区间分为多个小区间，然后在每个区间分别使用图6所示的迭代算法。如果区间划分过大，这种分子区间带来的效果不太明显；如果过小，则对于阻抗变化平坦的区间本身就是一种浪费，因此根据经验进行折中，选择200～300Hz作为子区间长度。

假设待测频率区间［a，b］被划分为m个子区间，分别记为［xi，xi+1］，其中i=0，1，…，m 且a=x0，xm=b，为保证总误差满足（a，b）≤ε，如果定义单位误差

一个解决方法就是定义子区间误差

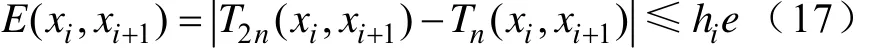
式中，hi=xi+1-xi。因为如果式（17）满足，则

因此，式（17）可以作为各个子区间上，基于二叉树结构的阻抗测量方法的迭代终止判断准则。

2.5二叉树结构测量方法在对数坐标下的应用

在前面的分析中，频率点的分布都是在线性坐标下讨论的，实际系统的阻抗测量与分析中，对数坐标也是很常用的一种形式。事实上，线性坐标可以根据下式转化为对数坐标

在基于二叉树的阻抗测量方法中，当用X替换x并采用f（10X）计算对应函数值时，测量得到的数据点就会等间隔地分布在对数坐标系中。

3　测量结果的校验

在基于分段二叉树结构的阻抗测量迭代过程中，式（13）和式（14）的本质是采用误差三角形面积来判断测量结果是否满足要求。对于某些情况，如图7所示，当新增加数据点D、E时，由于△ADC和△BCE的面积近似相等，导致T2n≈Tn，从而出现错误的误差估计，迭代结束，得到不准确的测量结果。

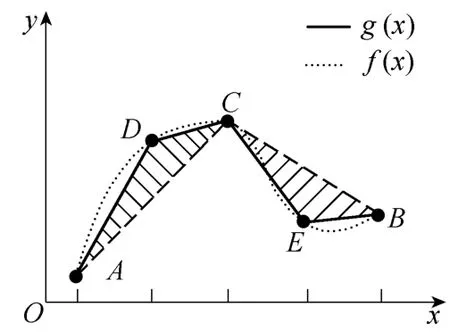
图7　错误的误差估计现象Fig.7　Wrong error estimation phenomenon

为了避免这样的错误，需要对测量结果的准确性进行校验，为此，需要首先建立误差给定值e和测量结果准确性之间的数学关系。

图8　误差分析示意图Fig.8　Error analysis for the proposed method

假设图8中，g（x）表示测量结果，f（x）表示阻抗特性曲线的真实值，点D和G分别是f（x）在区间［l，m］和［m，u］上的任意一点，由前面的分析可知区间［l，u］上的误差为

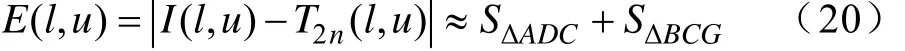
式中，SΔADC和SΔBCG分别表示△ADC和△BCG的面积，根据图8中的几何关系，可得

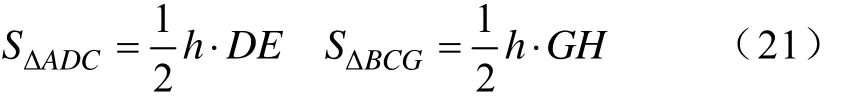
由式（20）和式（21）可得区间［l，u］的误差估计

根据式（17）和式（22），可以推导出

根据本文提出的二叉树结构阻抗测量方法的特点，最终得到的阻抗曲线包含2n+1个数据点和2n对如［l，m］和［m，u］这样的子区间。将图8中式（23）给出的结论推广到任意情况，可得

式（24）表明，阻抗特性曲线的测量值和真实值之间的平均误差小于2e/3。

从另一方面来说，如果最终测量得到的2n+1个数据点记为xi，其中i=1，2，…，2n+1。仿照图8，可以分为n对子区间［x2i-1，x2i+1］（i=1，2，…，n）。定义任意区间［x2i-1，x2i+1］（i=1，2，…，n）上的平均误差

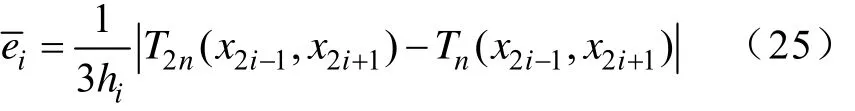
式中，hi=x2i+1-x2i-1。根据式（24），如果ei＜ 2e3，表明测量结果符合准确性要求，否则，需要按照图6中的二叉树结构重新测量。

对于图7中给出的错误现象，测量结果虽然满足图6中的迭代终止条件，但测量结果不能通过上述平均误差校验，因此需要继续迭代直到获得准确的阻抗测量结果。通过反复的迭代和误差校验，可以保证最终获取的阻抗特性曲线的准确性。

4　阻抗测量结果的量化指标

为了定量描述和比较测量结果的准确性的测量时间，需要对测量结果进行量化描述。

在基于分段二叉树结构的阻抗测量方法中，相关计算和判断主要为线性运算，这些计算花费的时间，相对于扰动信号注入、数据测量和使用傅里叶变换计算阻抗等花费的时间，可以忽略不计。因此，阻抗测量的时间可以近似用注入扰动信号的次数来衡量。基于上述分析，选取描述测量时间的量化指标为测量点数，即N=2n+1。

按照式（25）定义的平均误差，根据现代测试技术［19］，定义平均误差的算术平均值

平均误差的标准差

5　实验结果

为了证明本文所提方法的有效性，实验分别测量了单相AC系统和三相AC系统的阻抗。扰动信号注入和阻抗测量装置如图9所示，包括功率放大器、DSP控制板、霍尔传感器和工业控制计算机。其中，功率放大器在DSP的控制下实现扰动信号注入；传感器和数据采集卡用于获取实验数据；工业控制计算机进行数据处理和计算。

图9　阻抗测量实验装置Fig.9　Impedance measurement equipment

当测量电力电子系统阻抗时，扰动信号一般在源和负载的接口处注入，如图1和图2所示。由于硬件条件的限制，使用与电网相连接的调压器作为系统的源，负载由RLC构成。阻抗测量中，扰动信号在源和负载之间的接口处注入，其方式和标准电力电子系统阻抗测量一致。因此，本文的实验电路可以认为是一个简化的电力电子系统。

图10　单相交流系统Fig.10　Single-phase AC system

图11　三相交流系统Fig.11　Three-phase AC system

实验中，单相交流系统如图10所示，三相交流系统如图11所示。电路中的元件参数相同，具体数值如下：L1=2.8mH、R1=9.5Ω，L2=3.75mH、R2=1.5Ω，C3=0.07mF，R3=0.2Ω，电源有效值70V，50Hz，Rs= 10Ω。

在测量单相交流系统负载阻抗时，采用式（5）中定义的幅值和相角进行计算和迭代。具体参数设定如下：阻抗测量范围10～1 000Hz，近似等间隔地分为五个子区间，幅值和相位的误差给定eA=0.5Ω，eθ=3°，注入扰动电流幅值250mV。使用基于分段二叉树结构得到的阻抗测量结果如图12所示，其中，N=23，=0.1515，=0.3317，σA=0.0416，σθ=0.099 2；当使用传统扫频法测量23个数据点时，结果如图13所示，其中，σA=0.166 5，σθ=0.267 5。在测量点数相同时，相对于传统的扫频法，本文提出的方法减小48%，减小31%，且σA和σθ更小。

图12　基于分段二叉树结构的单相阻抗测量结果Fig.12　Measured results for single-phase AC system with binary tree structure

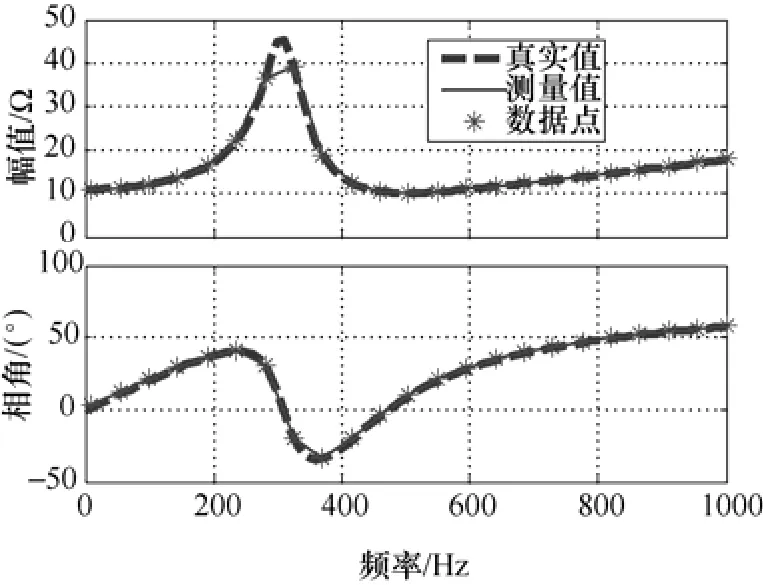
图13　基于传统扫频法的单相阻抗测量结果Fig.13　Measured results for single-phase AC system with frequency sweep method

在测量三相交流系统负载阻抗时，采用式（6）中定义的实部和虚部进行计算和迭代。具体参数设定如下：阻抗测量范围10～1 000Hz，近似等间隔地分为五个子区间，实部和虚部的误差给定eR= 0.5Ω，eI=0.5Ω，注入扰动电流幅值250mV。使用基于分段二叉树结构的阻抗测量方法得到的结果如图14所示，其中，N=29；当使用传统扫频法测量29个数据点时，结果如图15所示。

图14　基于分段二叉树结构的阻抗测量结果Fig.14　Measured results for three-phase AC system with binary tree structure

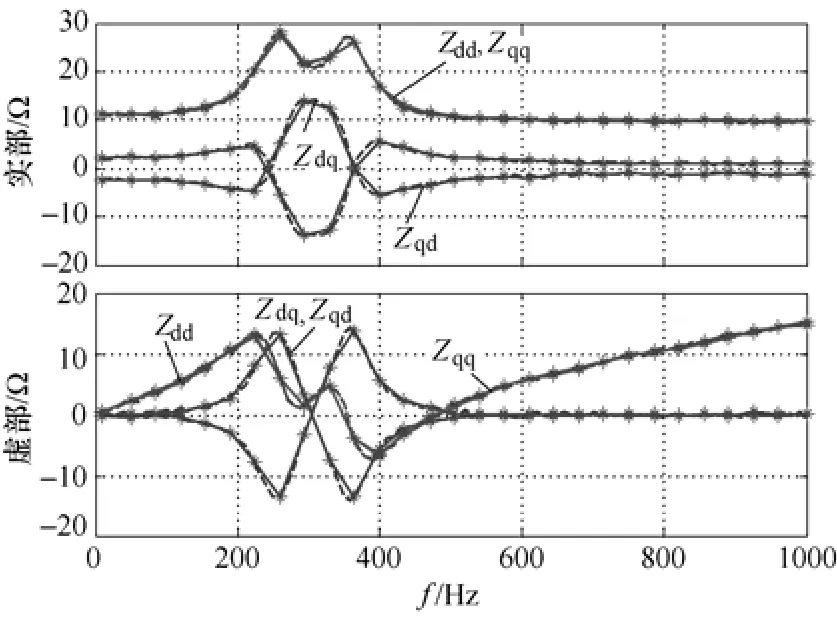
图15　基于传统扫频法的单相阻抗测量结果Fig.15　Measured results for single-phase AC systemwith traditional frequency sweep method

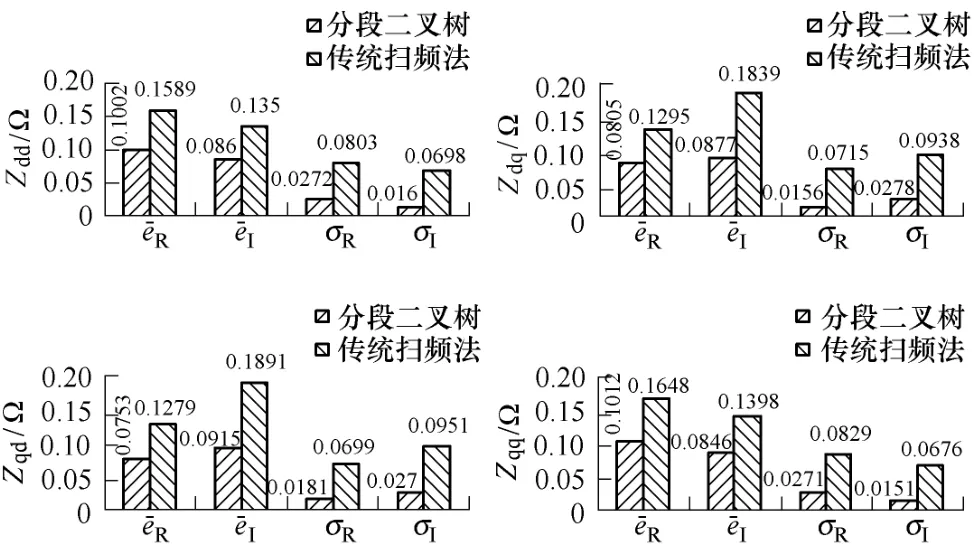
图16　两种阻抗测量方法的量化比较Fig.16　Comparison between the two methods

6　结论

本文建立了扫频法中频率间隔和测量结果准确性之间的数学关系，并在此基础上提出了一种分段二叉树结构的电力电子系统阻抗测量方法，可以根据待测网络的阻抗特性曲线和给定的测量结果误差自动选择合适的频率间隔，达到既满足测量的准确性，又不浪费测量时间的目的，提高了阻抗测量的效率和可靠性。由于阻抗可以认为是输入或输出电压、电流之间的传递函数，因此，对于其他采用正弦扰动测量系统传递函数的场合，本文提出的方法也是适用的。

［1］ Emadi A，Khaligh A，Rivetta C H，et al. Constant power loads and negative impedance instability in automotive systems： definition，modeling，stability，and control of power electronic converters and motor drives［J］. IEEE Transactions on Vehicular Technology，2006，55（4）： 1112-1125.

［2］ Middlebrook R D. Input filter considerations in design and application of switching regulators［C］. IEEE Industrial Application Society Annual Meeting，Chicago，USA，1976： 366-382

［3］ 马瑜，邱苍宇，张军明，等. 全桥DC-DC变流器模块阻抗特性研究［J］. 电工技术学报，2007，22（7）： 42-46.

Ma Yu，Qiu Cangyu，Zhang Junming，et al. Research on impedance characteristics of full bridge DC-DC converter modules［J］. Transactions of China Electrotechnical Society，2007，22（7）： 42-46.

［4］ 姚雨迎，张东来，徐殿国. 级联式DC-DC变换器输出阻抗的优化设计与稳定性［J］. 电工技术学报，2009，24（3）： 147-152.

Yao Yuying，Zhang Donglai，Xu Dianguo. Output impedance optimization and stability for cascade DC-DC converter［J］. Transactions of China Electrotechnical Society，2009，24（3）： 147-152.

［5］ Liu Jinjun，Feng Xiaogang，Lee F C. Stability margin monitoring for DC distributed power systems via perturbation approaches［J］. IEEE Transactions on Power Electronics，2003，18（6）： 1254-1261.

［6］ Feng Xiaogang，Liu Jinjun，Lee F C. Impedance specifications for stable DC distributed power systems［J］. IEEE Transactions on Power Electronics，2002，17（2）：157-162.

［7］ Sun J. Input impedance analysis of single-phase PFC converters［J］. IEEE Transactions on Power Electronics，2005，20（2）： 308-314.

［8］ Sun J，Colon J. Input impedance modeling of line-frequency rectifiers by the method of impedance mapping［C］. IEEE Workshops on Computers in Power Electronics，2006： 69-75.

［9］ Huang Jing，Corzine K A，Belkhayat M. Small-signal impedance measurement of power electronics based AC power systems using line-to-line current injection［J］. IEEE Transactions on Power Electronics，2009，24（2）：445-455.

［10］ Sun J. Impedance-based stability criterion for gridconnected inverters［J］. IEEE Transactions on Power Electronics，2011，26（11）： 3075-3078.

［11］ Familiant Y A，Huang Jing，Corzine K A，et al. New techniques for measuring impedance characteristics of three-phase AC power systems［J］. IEEE Transactions on Power Electronics，2009，24（7）： 1802-1810.

［12］ Belkhayat M，Williams M L. Impedance extraction techniques for DC and AC systems［C］. Proceedings of the Naval Symposium on Electric Machines，2000.

［13］ Familiant Y L，Corzine K A，Huang Jing，et al. AC impedance measurement techniques［C］. IEEE International Conference on Electric Machines and Drives，2005： 1850-1857.

［14］ Xiao Peng，Venayagarnoorthy G K，Corzine K A，et al. Recurrent neural networks based impedance measurement technique for power electronic systems［J］. IEEE Transactions on Power Electronics，2010，25（2）： 382-390.

［15］ 童立青，钱照明，邝乃兴，等. 一种新型在线系统阻抗测量方法［J］. 电工技术学报，2008，23（1）： 137-142.

Tong Liqing，Qian Zhaoming，Kuang Naixing，et al. Anovel on-line measurement for system impedance［J］. Transactions of China Electrotechnical Society，2008，23（1）： 137-142.

［16］ Yue Xiaolong，Zhuo Fang，Zhang Zhenghua. Impedance measurement based on binary tree and stack structure［C］. IEEE ECCE Asia，2013： 626-630.

［17］ 凌永祥，陈明逵. 计算方法教程［M］. 西安：西安交通大学出版社，2009.

［18］ 严蔚敏，吴伟民. 数据结构： C语言版［M］. 北京：清华大学出版社，1997.

［19］ 申忠如，郭福田，丁晖. 现代测试技术与系统设计［M］. 西安： 西安交通大学出版社，2009.

Segmented Binary Tree Method for Power Electronic System Impedance Measurement

Yue XiaolongZhuo FangZhang ZhenghuaShi HongtaoZhang Dong
（Xi'an Jiaotong UniversityXi'an710049China）

Impedance measurement is very important in power electronic based systems because of the close relationship between impedance and stability. However，traditional frequency sweep method always selects the equal frequency interval without guiding theory，which results in low accuracy，low reliability and low efficiency. In this paper，the relationship between measured result and the frequency interval is built firstly，then a segmented binary tree method for power electronic system impedance measurement is proposed. With this method，injection frequency points can be selected automatically according to the requirement of measurement accuracy. Compared to the traditional frequency sweep method，the proposed one can measure impedance more accurately and efficiently. The experimental results validate the effectiveness of the proposed method.

Power electronics based systems，impedance measurement，frequency sweep，binary tree，error calibration

TM46； TM934

岳小龙男，1989年生，博士研究生，研究方向为电子电子系统建模、稳定性分析及参数测量。

卓放男，1962年生，教授，博士生导师，研究方向为电能质量控制、光伏逆变器控制、微型电网参数测量及稳定性分析等。

国家自然科学基金项目（51177130）和台达2011电力电子科教发展计划重点项目（DREK2011002）资助。

2013-12-31改稿日期 2014-04-22