基于互补免疫算法的变压器故障诊断
2015-10-25苑津莎张利伟张英慧
苑津莎 张利伟 李 中 张英慧
(1. 华北电力大学电气与电子工程学院 保定 071003
2. 冀北电力公司检修分公司 北京 102400)
基于互补免疫算法的变压器故障诊断
苑津莎1张利伟1李中1张英慧2
(1. 华北电力大学电气与电子工程学院保定071003
2. 冀北电力公司检修分公司北京102400)
基于自组织抗体网络(soAbNet)的变压器故障诊断方法中没有网络压缩机制,并且网络的初始抗体是随机选取的,网络性能不稳定。针对这一问题,提出了基于互补免疫算法的变压器故障诊断方法,结合变压器故障诊断的特点详细设计了免疫算子以弥补soAbNet的不足。免疫算子中接种疫苗利用K-means最佳聚类算法为soAbNet提供初始抗体,并通过免疫选择压缩网络规模,其参数由粒子群算法进行优化。变压器故障诊断实验结果表明,所提出的互补免疫算法能够充分利用系统的先验知识,并有效地提取故障样本的数据特征,与单一智能方法相比具有更高的诊断准确率。
变压器故障诊断人工免疫系统免疫算子互补策略
0 引言
变压器是输送电能的重要设备之一,其可靠性直接影响到电力系统的安全与稳定[1-3]。油中溶解气体分析(Dissolved Gas Analysis, DGA)技术能尽早地发现设备内部存在的潜伏性故障,并随时监视故障的发展情况,是监督油浸式电力变压器安全运行的最有效措施之一。由于一般不需要设备停电,人们正在利用DGA技术开展在线检测,并取得了一定的成果。
电力变压器故障的产气机理复杂,仅靠人为实验总结难以归纳出故障征兆与故障类型之间的关系。随着人工智能研究的进展,各种智能方法相继被引入电力变压器的故障诊断中。这些新的诊断方法克服了IEC三比值法的不足,提高了诊断的准确率。但由于每种智能算法各有优缺点,单独应用于变压器故障诊断时存在一定的局限[4-6]。多种智能方法的综合集成成为了当前人工智能领域中的一个研究热点,也是探索变压器故障诊断的新途径[7,8]。
人工免疫系统是一种模仿自然免疫系统功能的智能方法,在故障诊断领域的应用获得了广泛的关注[9-14]。文献[15]提出了一种自组织抗体网络(self-organization Antibody Net,soAbNet),采用抗体生成算法实现抗体对抗原的高效学习,并将其应用于变压器故障诊断。但该算法存在以下两个方面的不足:①soAbNet中没有网络压缩机制,训练后的网络中存在冗余抗体;②网络的初始抗体是随机选取的,而学习过程对初始抗体的选取比较敏感,网络性能并不稳定。
基于智能互补策略融合的观点,本文在soAbNet的基础上引入了免疫进化算法中的免疫算子,提出了一种互补免疫算法。免疫算子主要通过接种疫苗和免疫选择两个步骤来完成[16]。接种疫苗利用系统的先验知识来构造疫苗,可提高免疫网络的效率,使网络性能更加稳定;免疫选择对应于免疫调节机制,可以去除冗余抗体,优化网络结构。
结合soAbNet和电力变压器故障诊断的特点,本文对免疫算子进行了详细设计,并提出了基于互补免疫算法的变压器故障诊断方法。接种疫苗利用K-means最佳聚类算法从变压器故障样本中提取疫苗,以获得的疫苗作为免疫网络的初始抗体;免疫选择则通过免疫检测和抗体选择来简化网络结构,其参数亲和度阈值通过粒子群优化算法进行优化;而自组织抗体网络可以实现对变压器故障样本的快速学习和识别。该方法可以获取更好的表征故障样本特征的记忆抗体集,以提高诊断正确率。
1 自组织抗体网络
自组织抗体网络忽略抗体与T细胞的差异,将两者统一抽象为抗体,由若干不同类型的抗体为节点构成,相同类型的抗体连接在一起,形成一个连通子图[15]。每个抗体(节点)具有一定的浓度,浓度作为该节点的权值,表示该抗体识别抗原能力的强弱,整个网络的结构可表示为一个带权的不完全连通图,如图1所示。在图1中,有三类抗体,其类别分别用1、2和3表示,同类抗体通过类别信息相连接,c为抗体浓度。免疫抗体网络中,每个抗体对各种抗原都具有识别、效应和记忆的功能,抗体之间相互作用,共同完成对抗原的学习、记忆和识别。
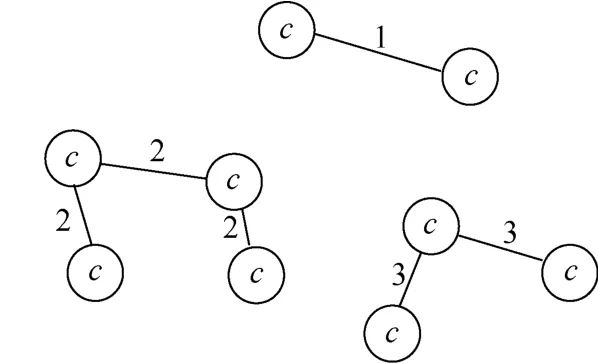
图1 自组织抗体网络示意图Fig.1 Self-organization antibody net
1.1抗原、抗体编码
形态空间是源于理论免疫学的概念,用于描述利用计算手段研究抗体-抗原关系时所处的数学空间环境[11]。在自组织抗体网络中,抗原和抗体被视为其形态空间中的点,采用实数编码并且具有不同的结构。
(1)抗原编码。抗原(Antigen,Ag)是指待分析的数据样本。每个抗原被视为其形态空间中的一个点,对应于一条数据样本的n维特征向量,用实数向量Agj来表示
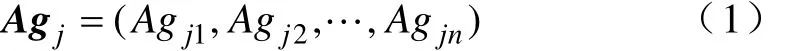
(2)抗体编码。抗体(Antibody,Ab)是指免疫算法产生的反映抗原特征的数据。抗体编码包括所属类别、抗体浓度和抗体属性三部分。抗体的结构可表示为
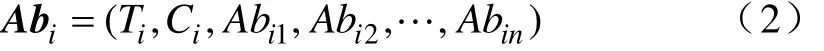
式中,Ti代表抗体Abi所属的类别,也是抗体Abi所能识别的抗原类型;Ci代表抗体Abi的浓度,也是抗体Abi所能识别抗原的数量;Abi1~Abin分别表示抗体的特征属性。
1.2学习与记忆策略
(1)抗体进化。网络中的抗体通过调整浓度和属性值,实现对抗原的学习和记忆。抗体Abi对输入抗原Agj的快速学习和记忆,按式(3)来计算。
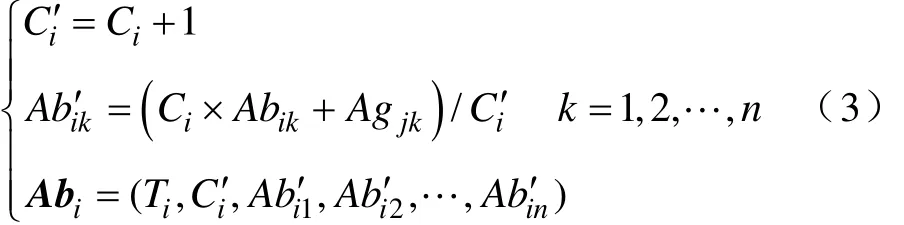
(2)抗体合并。在人工免疫系统中,亲和度通常用数据之间的距离表示,用于表明两个抗体之间的相似度。抗体合并是将亲和度小于一定阈值的两个同类抗体合并为一个新抗体。具体步骤是,抗体Abi与Abj合并成为一个新抗体Abk,原有抗体Abi和Abj从自组织抗体网络中删除。抗体Abk按式(4)计算。
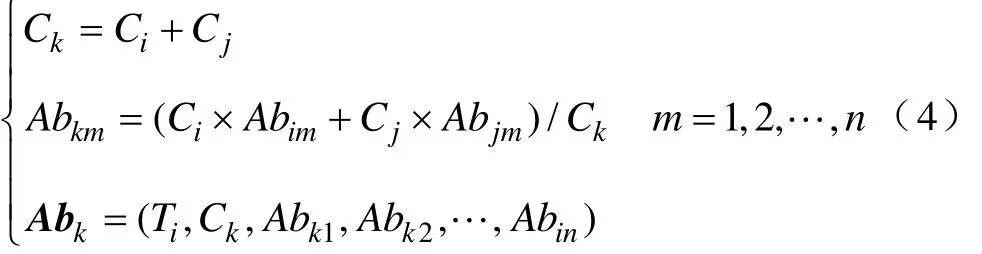
(3)抗体新生。如果已有抗体无法正确识别输入抗原,网络自动生成一个新抗体,完成对输入抗原的学习和记忆。新抗体Abi按式(5)计算,其中Agj为输入抗原。
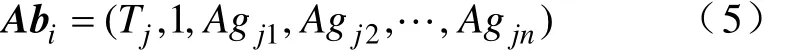
1.3算法流程
自组织抗体网络的具体算法步骤如下:(1)设置初始抗体个数K,随机选择初始抗体。(2)检验停止准则,如果满足,则停止,否则转到(3)。
(3)计算输入抗原Agj与网络中所有抗体的亲和度,得到相异度矩阵D。
①根据相异度矩阵D,选取识别抗体Abr,即与Agj亲和度最高的抗体。
②如果Abr和Agj的类别不一致,网络发生抗体新生,返回(3)。
③Abr和Agj的类别一致,Abr即为最佳识别抗体Abb,令Abb=Abr。
④计算Abb与网络中同类抗体的亲和度,选择与Abb亲和度最高的同类抗体,记为Abj。
⑤如果Abb与Abj的亲和度高于Abb与Agj的亲和度,根据Agj发生抗体新生,同时Abb和Abj发生抗体合并,返回(3)。
⑥如果Abb与Abj的亲和度低于Abb与Agj的亲和度,Abb根据Agj发生抗体进化,返回(3)。
(4)返回(2)。
这里,亲和度用欧几里德二次方距离衡量,距离越小,亲和度越高。网络训练的停止准则为连续的两次训练后,网络中各类抗体的数目不再发生变化。网络对抗原的识别过程是计算待识别的抗原与记忆抗体之间的亲和度,用最邻近规则进行分类。
2 免疫算子设计
免疫算子是在合理提取疫苗的基础上,通过接种疫苗和免疫选择两个操作步骤来完成的[16]。前者是为了提高适应度,后者则是为了防止群体的退化。其中,疫苗是指依据人们对待求解问题所具备的或多或少的先验知识,从中提取出的一种基本的特征信息,可以看作是对待求的最佳个体所能匹配模式的一种估计。需要说明的是,选取疫苗的优劣,只会影响到免疫算子中接种疫苗作用的发挥,不至于影响算法的收敛性。因为免疫算法的收敛性归根结底是由免疫算子中的免疫选择来保证的[16]。
2.1接种疫苗
通常,人工免疫系统中初始抗体是随机产生的,没有充分利用系统的先验信息。而网络的学习过程和训练结果对初始抗体的选取比较敏感。
接种疫苗根据待求解问题的特征信息来制作免疫疫苗,以一定的强度干预全局并行的搜索进程。一般可以选用智能方法如神经网络和聚类算法等来提取疫苗。由于提取疫苗只是形成关于数据的粗略描述,能反映数据分布特征即可,对疫苗个数没有严格要求。
K-means算法是局域原型的目标函数聚类方法的典型代表,简单、快速,适合对数值型数据聚类[17]。在变压器油中溶解气体分析中,故障特征向量都是数值型的,并且故障样本有限,适合于利用K-means算法获取疫苗。对待学习的训练样本进行具体分析,按类别分别进行K-means聚类,然后以得到的聚类中心作为免疫疫苗,直接植入免疫网络中作为初始抗体。各类别训练样本的聚类个数依据其复杂度确定。
假设训练样本中第i类变压器故障样本Xi的样本个数为Ni(i=1, 2,…, M),M为变压器故障类型的个数。
对第i类变压器故障样本Xi的Ni个样本进行K-means聚类,算法流程如下:
(1)初始化。随机指定Ki(i=1, 2,…, M)个聚类中心(z1, z2,…,zKi)。
(2)分配xj,j=1,2,…, Ni。对每一个样本xj,找到离它最近的聚类中心zv,并将其分配到zv所标明的故障类型。
(3)根据聚类结果,重新计算聚类中心(z1, z2,…,zKi)。
(5)如果D值收敛,则返回(z1, z2,…,zKi)并终止本算法;否则,返回(2)。
由于K-means算法需要预先给定聚类数目Ki,通常使用内部有效性指标评估多次聚类结果的质量来确定数据集的最佳聚类数。
这里,内部有效性指标使用CH(calinskiharabasz)指标[18]。CH指标是基于全部样本的类内离差矩阵和类间离差矩阵的测度,其最大值对应的聚类数目作为最佳聚类数Ki。设k表示聚类数,trB(k)与trW(k)分别表示类间离差矩阵的迹和类内离差矩阵的迹。CH指标定义为

结合本文获取变压器故障疫苗的具体情况,第i类故障疫苗数目即聚类个数Ki的具体确定方法如图2所示。聚类数k的范围为[Kmin, Kmax],通常取Kmin=2,使用经验公式,Ni为第i类变压器故障样本Xi的样本个数。
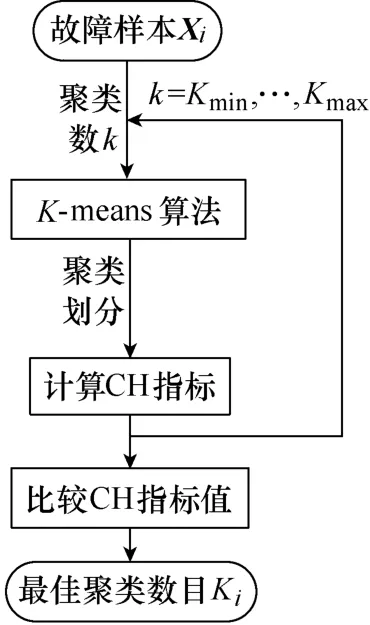
图2 最佳聚类数Ki的确定方法Fig.2 The method for determining optimal number of clusters
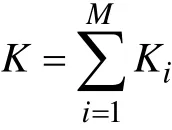
2.2免疫选择
soAbNet的学习算法中没有网络压缩机制,记忆抗体中存在很多冗余抗体,导致网络规模过大,网络效率降低。但是在免疫系统中,能够生成的抗体数目是有限的,不可能无限制地增长。免疫算子中的免疫选择对应于生物免疫系统中的免疫调节,实现对记忆抗体的优化,以保证网络的稳定。
免疫选择由免疫检测和抗体选择两个步骤完成。
第一步是免疫检测,即计算同类别抗体间的亲和度,分析抗体的分布情况。这里,亲和度用抗体属性间的欧几里得二次方距离衡量,距离越小,亲和度越高。同类抗体Abi和抗体Abj之间的亲和度计算方法为
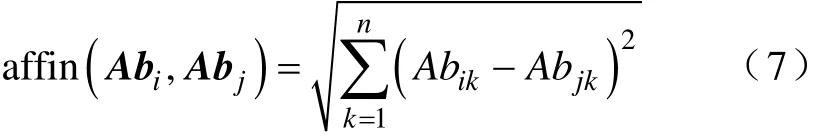
第二步是抗体选择,即亲和度值低于亲和度阈值σ 的同类抗体发生抗体合并,可以简化网络结构,控制网络规模。抗体合并是soAbNet的学习策略之一,同类抗体Abi和抗体Abj发生抗体合并,产生新抗体Abk的计算方法同式(4)。
σ 是亲和度阈值,它通过调整网络中抗体的特异性水平来控制网络的可塑性和学习准确度。一般可取一个较小的值(例如σ ≤0.1),然后逐步增大其值,并分析目标函数值,以便最终确定一个合适的网络参数。
2.3参数优化
对自组织抗体网络进行训练时只需要设定初始抗体个数K。本文提出的互补免疫算法利用接种疫苗为自组织抗体网络提供初始抗体,初始抗体个数由K-means最佳聚类的聚类结果决定,不需要预先设置。此外,需要调整的参数只有免疫选择中涉及的亲和度阈值σ。
免疫选择中亲和度阈值σ 的取值对本文免疫算法的学习结果有重要影响。σ 的取值越大,训练得到的记忆抗体就越少。但是σ 的取值大到一定程度时,记忆抗体太少,并不能准确提取待学习数据的分布特征。σ 的取值越小,得到的记忆抗体越多,而训练后的网络中就会存在冗余抗体。通常,σ 的取值是通过计算并分析多次实验的结果来确定的。
为了消除人为主观因素的影响,本节采用粒子群优化算法对亲和度阈值σ 进行优化。粒子群优化算法(Particle Swarm Optimization,PSO)是计算智能领域内一种基于群体智能的优化算法[19]。
选取免疫算法的故障诊断正确率作为PSO的适应度评价函数,计算其最大值。需要设置的关键参数有:待定参数亲和度阈值σ 的取值范围;每步迭代允许的最大变化量即最大速度,一般取待定参数取值范围的10%~20%。利用PSO对亲和度阈值σ 进行优化的算法步骤如下:
(1)PSO初始化。设置上文提及的关键参数及群体规模、粒子维数和迭代次数等参数,随机初始化粒子速度和位置。
(2)根据粒子位置即亲和度阈值σ ,利用经免疫选择优化后的记忆抗体集,对测试样本进行故障诊断,输出适应度评价函数即故障诊断正确率。
(3)根据适应度值确定个体极值和群体极值。
(4)检查是否满足终止条件,若满足则过程终止,输出优化结果;若不满足,则转到(5)。
(5)更新粒子速度和位置,返回(2)。
利用PSO对亲和度阈值σ 进行优化的算法流程如图3所示。
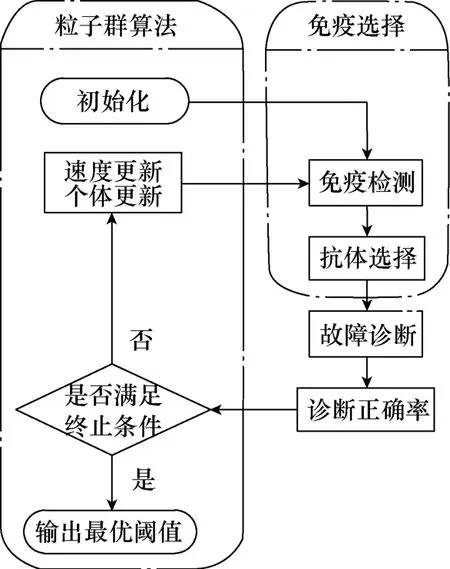
图3 利用PSO优化亲和度阈值的流程Fig.3 Flowchart of affinity threshold optimization using PSO
3 基于互补免疫算法的变压器故障诊断
3.1故障特征向量
对判断油浸式变压器内部故障有价值的气体为氢气(H2)、甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)、乙炔(C2H2)、一氧化碳(CO)和二氧化碳(CO2),称这些气体为特征气体[20]。与改良三比值法相同,本文利用前五种特征气体含量进行分析。CH4、C2H6、C2H4和C2H2含量的总和称为总烃,即烃类气体含量的总和。
根据模拟实验和大量的现场试验可以发现,研究变压器内部不同故障产生特征气体的规律时,不只分析油中溶解气体的组分含量,还应该考虑气体的相对含量,即H2在氢烃气体中所占的比例以及CH4、C2H6、C2H4和C2H2在总烃分别所占的比例。这里,用φ (H2)、φ (CH4)、φ (C2H6)、φ (C2H4)和φ (C2H2) 分别表示H2、CH4、C2H6、C2H4和C2H2的含量,用T表示氢烃气体总和,用C表示总烃含量。则故障特征向量xi可以表示为
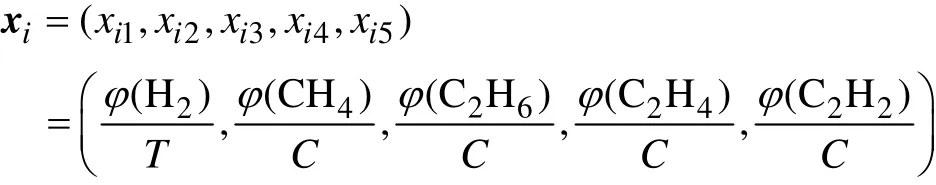
式中,xij∈[0,1],i=1,2,…,N;j=1,2,…,5,对应于特征向量xi的5个属性,N为故障样本的数目。
例如,某变压器的油中溶解气体组分含量为φ (H2)=279×10-6,φ (CH4)=41×10-6,φ (C2H6)=42× 10-6,φ (C2H4)=9.7×10-6,φ (C2H2)=34×10-6,故障类型为高能放电(D2)。在基于互补免疫算法的变压器故障诊断模型中,该条故障样本对应的输入特征向量为x=(0.687 7, 0.323 6, 0.331 5, 0.076 56, 0.268 4)。
3.2故障类型
变压器的故障类型一般分为放电型和过热型两大类,但实际中放电和过热可能同时发生。参照改良三比值法[20]和IEC 60599—2007[21]的规定,本文考虑如下八种故障模式:低温过热T1(低于300℃),中温过热T2(300~700℃),高温过热T3(高于700℃),局部放电或受潮PD,低能放电D1,高能放电D2,低能放电兼过热MF1,高能放电兼过热MF2。因此,算法中变压器故障类型的个数M=8。
在免疫算法中,用{i|i=1,2,…,8}分别表示故障类型T1、T2、T3、PD、D1、D2、MF1和MF2,则待学习抗原编码和抗体编码中的类别t可以表示为
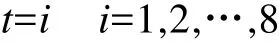
3.3抗原、抗体编码
传统的人工免疫网络属于无监督学习算法,得到的记忆抗体没有故障类别的信息,无法给出其准确类别[13]。本质上,电力变压器故障诊断属于模式识别,而收集的电力变压器故障样本故障类型明确并且样本数量有限,更适合于使用监督式学习。根据监督式学习的特点,综合文献[13,15],本文方法的抗原和抗体采用不同的编码方式。
(1)抗原编码。抗原编码分为两类,即待识别抗原的编码和待学习抗原的编码。
待识别的抗原不包含类别信息,用一个5维实数向量Agi来表示,对应故障特征向量xi。
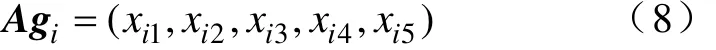
待学习的抗原由于其所属故障类型已知,在抗原编码中加入类别信息用于监督式学习,ti是待学习的抗原Agi所属的故障类别。
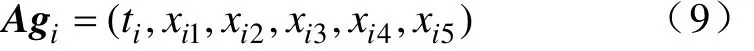
(2)抗体编码。抗体包含了输入模式的特征信息,其编码包括抗体所属的故障类别ti、抗体的浓度ci和故障特征向量xi三个部分。
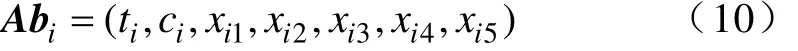
3.4故障诊断流程
文中提出的互补免疫算法中,免疫算子利用K-means聚类算法为自组织抗体网络提供初始抗体,自组织抗体网络实现对故障样本集的学习,免疫选择对记忆抗体集进行优化,最后利用记忆抗体集对待识别样本进行故障诊断。该互补免疫算法的流程如图4所示。
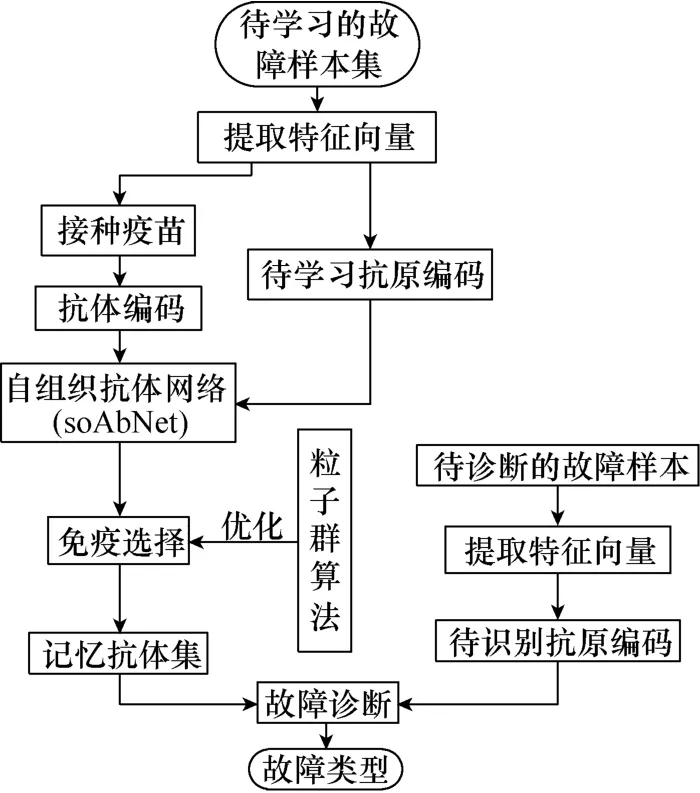
图4 互补免疫算法流程Fig.4 Flowchart of complementary immune algorithm
具体流程如下:
(1)数据预处理。对待学习和待诊断的变压器故障样本按照文中选取的特征向量进行预处理,得到训练样本和测试样本并分别进行抗原编码。
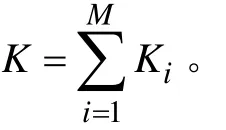
(3)对接种疫苗得到的K个聚类中心进行抗体编码,并作为自组织抗体网络的初始抗体。
(4)将初始抗体和训练样本输入到自组织抗体网络,对自组织抗体网络进行训练。
(5)免疫选择。通过免疫检测和抗体选择来优化自组织抗体网络学习得到的记忆抗体集,并采用粒子群算法对亲和度阈值σ 进行优化。
(6)计算测试样本与记忆抗体之间的亲和度,按照最邻近规则进行故障诊断,输出故障类型。
4 实验结果与分析
本文使用由冀北电力公司检修分公司提供的变压器油中溶解气体分析检测记录和从文献中收集的故障样本共358组。为了提高本文互补免疫算法的性能,利用基于最邻近规则的样本选择方法[22]来选择最具有代表性的训练样本,最终选取了181条样本作为训练样本集,剩余的177条样本作为测试样本集。实验平台为Matlab 7.6.0(R2008a),CPU为酷睿双核1.8GHz,内存为2G。
免疫算子中免疫接种根据CH指标对预处理后的训练样本按照故障类别分别进行K-means最佳聚类,得到带有样本分布特征的故障疫苗。表1列出了训练样本的分布情况、聚类数范围[Kmin, Kmax]和疫苗数目。
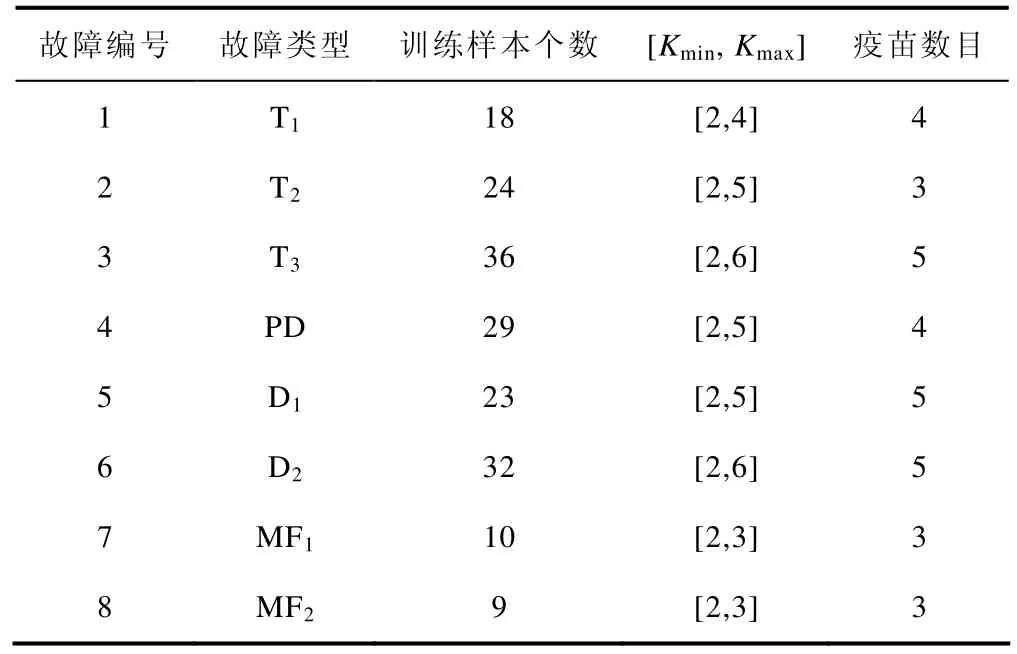
表1 训练样本分布及疫苗数目Tab.1 Distribution of training dataset and vaccination amounts
接种疫苗对K-means最佳聚类得到的32个聚类中心进行抗体编码,将其作为自组织抗体网络的初始抗体。确定初始抗体后,互补免疫网络通过自组织抗体网络完成对训练样本集的学习,最终得到记忆抗体集。
对于免疫选择时亲和度阈值σ 的取值,本文采用粒子群优化算法进行优化。根据所选取的故障特征向量的取值,待定参数σ 的取值范围设定为[0.1, 1.5],每步迭代允许的最大变化量即最大速度取为0.14。设定粒子种群数为10,每个粒子的维数为1,惯性权重ω=1,加速度因子1与加速度因子2均设置为1.5,最大迭代次数N=50,采用免疫算法的故障诊断正确率作为适应度函数。根据设定的参数,粒子群优化算法在迭代11次后达到收敛。这时亲和度阈值σ=0.381 2,免疫算法的故障诊断正确率最高为91.53%。优化过程中最优个体适应度值变化如图5所示。
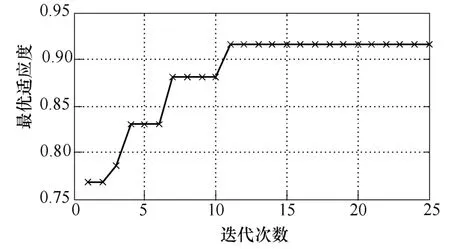
图5 最优适应度变化曲线Fig.5 Optimal fitness curve
免疫算子中抗体选择根据PSO优化得到的亲和度阈值σ=0.381 2优化记忆抗体集,优化前后的记忆抗体数目见表2。通过对比可以看出,抗体选择明显减少了记忆抗体集的数目,有效地去除了网络中的冗余抗体。
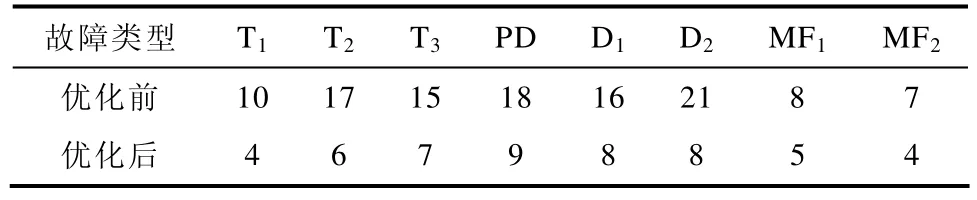
表2 记忆抗体数目对比Tab.2 Comparison of memory antibody number
为了分析本文提出的互补免疫算法的分类性能,在相同的训练样本集和测试样本集上分别采用BP神经网络、soAbNet和互补免疫算法进行学习和故障诊断,并和改良三比值法进行比较。各故障类型的诊断正确率见表3。从表中可以看出本文提出的互补免疫算法的诊断正确率明显高于IEC三比值法、BP神经网络和soAbNet。
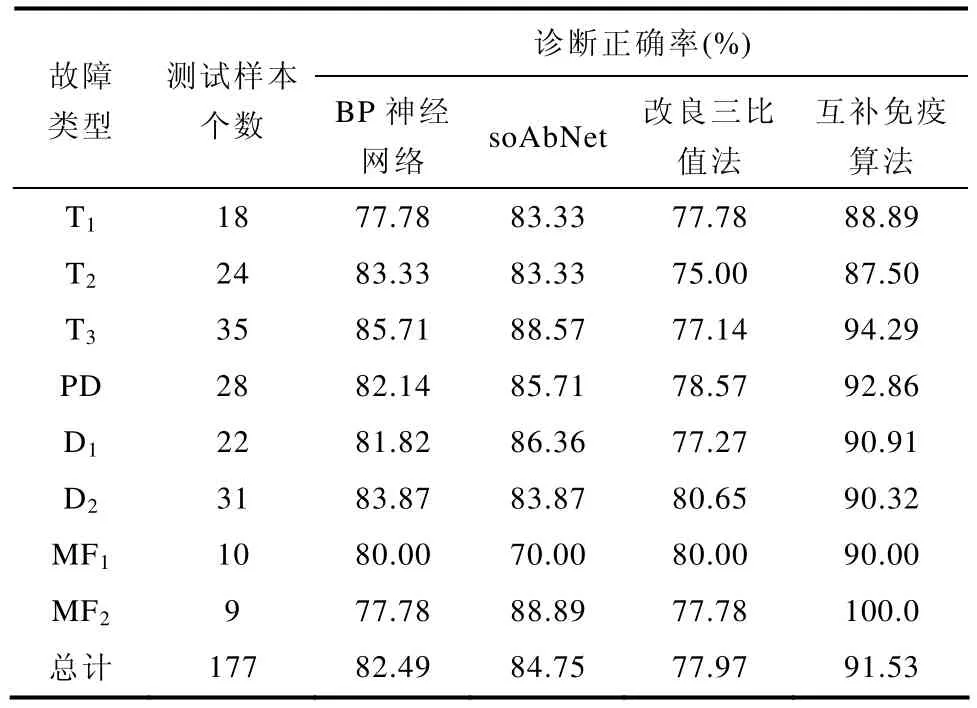
表3 不同方法的诊断结果比较Tab.3 Results comparison of different methods
为了进一步验证本文诊断方法的性能,将互补免疫算法和soAbNet分别在相同的训练样本集和测试样本集上进行了10次变压器故障诊断仿真实验并对比研究实验结果。10次仿真实验的记忆抗体个数对比如图6所示,诊断正确率对比如图7所示。
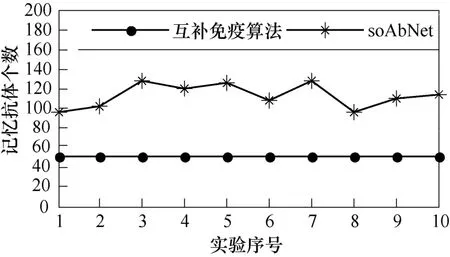
图6 记忆抗体个数对比Fig.6 Comparison of memory antibody numbers
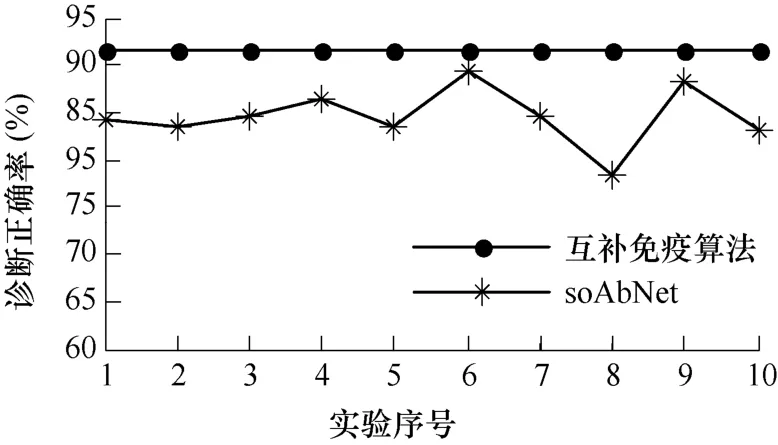
图7 诊断正确率对比Fig.7 Comparison of correct diagnosis rates
从图6可以看出,互补免疫算法的记忆抗体数目明显少于随机选取初始抗体的soAbNet,并且前者的记忆抗体数目更加稳定。从图7可以看出,互补免疫算法的诊断正确率明显高于soAbNet,并且比后者更加稳定。可见,将免疫算子引入免疫网络不但可以优化网络结构,而且使得网络性能更加稳定。
5 结论
本文提出了一种基于互补免疫算法的变压器故障诊断方法,详细设计了免疫算子以弥补自组织抗体网络(soAbNet)的不足。该方法将soAbNet和免疫算子综合集成,充分发挥每种智能方法的优势,实现了对不精确处理与精确处理的互补。
(1)接种疫苗利用K-means最佳聚类算法对变压器故障样本进行预处理,可以自适应的确定接种疫苗的数量并作为免疫网络的初始抗体,充分利用了系统的先验知识,网络性能比soAbNet更加稳定。
(2)免疫选择通过免疫检测和抗体选择有效地去除了冗余抗体,简化了网络结构。其参数亲和度阈值σ 则通过粒子群优化算法(PSO)进行优化,避免了人为选择的主观性。
(3)从变压器故障诊断实例分析来看,基于互补免疫算法的变压器故障诊断方法比IEC三比值法、BP神经网络和soAbNet等单一方法的诊断正确率高,具有更好的诊断效果。
(4)结合变压器故障诊断的特点,研究集成型智能诊断方法,为提高故障诊断的可靠性和智能化程度提供了新的思路,有助于实际工程应用。
[1] 孙才新, 陈伟根, 李俭, 等. 电气设备油中气体在线监测与故障诊断技术[M]. 北京: 科学出版社, 2003.
[2] 操敦奎. 变压器油色谱分析与故障诊断[M]. 北京:中国电力出版社, 2010.
[3] Tang W H, Wu Q H. Condition monitoring and assessment of power transformers using computational intelligence[M]. New York: Springer-Verlag Press, 2011.
[4] 刘娜, 高文胜, 谈克雄. 基于组合神经网络模型的电力变压器故障诊断方法[J]. 电工技术学报, 2003, 18(2): 83-86.
Liu Na,Gao Wensheng,Tan Kexiong. Fault diagnosis of power transformer using a combinatorial neural network[J]. Transactions of China Electrotechnical Society, 2003, 18(2): 83-86.
[5] 吴立增, 朱永利, 苑津莎. 基于贝叶斯网络分类器的变压器综合故障诊断方法[J]. 电工技术学报, 2005, 20(4): 45-51.
Wu Lizeng, Zhu Yongli, Yuan Jinsha. Novel method for transformer faults integrated diagnosis based on Bayesian network classifier[J]. Transactions of China Electrotechnical Society, 2005, 20(4): 45-51.
[6] 章剑光, 周浩, 项灿芳. 基于Super SAB神经网络算法的主变压器故障诊断模型[J]. 电工技术学报, 2004, 19(7): 49-52, 58.
Zhang Jianguang, Zhou Hao, Xiang Canfang. Application of Super SAB ANN model for transformer fault diagnosis[J]. Transactions of China Electrotechnical Society, 2004, 19(7): 49-52, 58.
[7] 王永强,律方成,李和明. 基于粗糙集理论和贝叶斯网络的电力变压器故障诊断方法[J]. 中国电机工程学报, 2006, 26(8): 137-141.
Wang Yongqiang, Lü Fangcheng, Li Heming. Synthetic fault diagnosis method of power transformer based on rough set theory and Bayesian network[J]. Proceedings of the CSEE, 2006, 26(8): 137-141.
[8] 张东波, 徐瑜,王耀南. 主动差异学习神经网络集成方法在变压器DGA故障诊断中的应用[J]. 中国电机工程学报, 2010, 30(22): 64-70.
Zhang Dongbo, Xu Yu, Wang Yaonan. Neural network ensemble method and its application in DGA fault diagnosis of power transformer on the basis of active diverse learning[J]. Proceedings of the CSEE, 2010, 30(22): 64-70.
[9] Timmis J, Neal M, Hunt J. An artificial immune system for data analysis[J]. Biosystems,2000,55(1-3):143-150.
[10] 丁永生, 任立红. 人工免疫系统: 理论与应用[J].模式识别与人工智能, 2000, 13(1): 52-59.
Ding Yongsheng, Ren Lihong. Artificial immune system: theory and applications[J]. Pattern Recognition and Artificial Intelligence, 2000, 13(1): 52-59.
[11] 焦李成, 杜海峰, 刘芳, 等. 免疫优化计算、学习与识别[M]. 北京: 科学出版社, 2003.
[12] Dasgupta D, Forrest S. Artificial immune systems in industrial applications[C]. Proceeding of the Second International Conference on Intelligent Processing and Manufacturing of Materials, Honolulu, HI, 1999.
[13] 熊浩, 孙才新, 陈伟根. 电力变压器故障诊断的人工免疫网络分类算法[J]. 电力系统自动化, 2006, 30(6): 57-60.
Xiong Hao, Sun Caixin, Chen Weigen. Artificial immune network classification algorithm for fault diagnosis of power transformers[J]. Automation of Electric Power Systems, 2006, 30(6): 57-60.
[14] 杜海峰, 王孙安. 基于ART-人工免疫网络的多级压缩机故障诊断[J]. 机械工程学报, 2002, 38(4): 88-90.
Du Haifeng, Wang Sunan. Fault diagnose of the reciprocating compressor based on ART-artificial immune network[J]. Chinese Journal of Mechanical Engineering, 2002, 38(4): 88-90.
[15] 李中, 苑津莎, 张利伟. 基于自组织抗体网络的电力变压器故障诊断[J]. 电工技术学报, 2010, 25(10): 200-206.
Li Zhong, Yuan Jinsha, Zhang Liwei. Fault diagnosis for power transformer based on the self-organization antibody net[J]. Transactions of China Electrotechnical Society, 2010, 25(10): 200-206.
[16] 焦李成, 王磊. 免疫进化算法[C]. 1999年中国神经网络与信号处理学术会议论文集, 汕头, 1999.
[17] 孙吉贵, 刘杰, 赵连宇. 聚类算法研究[J]. 软件学报, 2008, 19(1): 48-61.
Sun Jigui,Liu Jie,Zhao Lianyu. Clustering algorithms research[J]. Journal of Software, 2008, 19(1): 48-61.
[18] 周世兵. 聚类分析中的最佳聚类数确定方法研究及应用[D]. 无锡: 江南大学, 2011.
[19] 杨维, 李歧强. 粒子群优化算法综述[J]. 中国工程科学, 2004, 6(5): 87-94.
Yang Wei, Li Qiqiang. Survey on particle swarm optimization algorithm[J]. Engineering Science, 2004, 6(5): 87-94.
[20] 中华人民共和国国家质量监督检验检疫总局. GB/T 7252—2001 变压器油中溶解气体分析和判断导则[S]. 北京: 中国电力出版社, 2001.
[21] International Electrotechnical Commission (IEC). IEC 60599:1999 Mineral oil-impregnated electrical equipment in service-Guide to the interpretation of dissolved and free gases analysis[S]. Geneva: IEC, 1999.
[22] 郝红卫, 蒋蓉蓉. 基于最近邻规则的神经网络训练样本选择方法[J]. 自动化学报, 2007, 33(12): 1247-1251.
Hao Hongwei, Jiang Rongrong. Training sample selection method for neural networks based on nearest neighbor rule[J]. Acta Automatica Sinica, 2007, 33(12): 1247-1251.
Fault Diagnosis of Transformers Based on Complementary Immune Algorithm
Yuan Jinsha1Zhang Liwei1Li Zhong1Zhang Yinghui2
(1. North China Electric Power UniversityBaoding071003China
2. Jibei Electric Power Maintenance CompanyBeijing102400China)
The transformer fault diagnosis based on self-organization antibody net (soAbNet) has no network compression mechanism and selects the initial antibodies randomly, so its network performance is instable. Thus, a diagnosis method based on complementary immune algorithm for power transformer is proposed in this paper, and immune operator is designed in detail considering the characteristics of transformer fault diagnosis. Vaccination of immune operator uses K-means optimal clustering algorithm to provide initial antibodies for soAbNet and compresses the network through immune selection, and its parameter is optimized by particle swarm optimization (PSO) algorithm. Experimental results demonstrate that the proposed complementary immune algorithm could make use of prior knowledge and extract the data characteristics of the fault samples effectively. The diagnostic accuracy of the proposed algorithm is higher than that of the single intelligence algorithm.
Transformers, fault diagnosis, artificial immune system, immune operator, complementary strategy
TM411
苑津莎男,1957年生,教授,博士生导师,研究方向为智能信息处理,电磁场理论及其应用。
张利伟男,1983年生,博士研究生,研究方向为智能信息处理,电气设备故障诊断。(通信作者)
国家自然科学基金(61204027)和中央高校基本科研业务费专项资金(13XS26)资助项目。
2013-01-06改稿日期 2014-03-05
