三支决策理论及应用
2015-10-24柯德营刘传勇
殷 业,柯德营,刘传勇
(上海师范大学信息与机电工程学院,上海200234)
0 引言
三支决策作为一种方法早就被应用,但对这种方法的系统理论研究是最近十几年的事.加拿大里贾纳大学的姚一豫教授1989年提出了决策粗糙集理论[1],2009年又提出了三支决策理论[2],从而学术界开始了三支决策方法的系统理论研究[15-16].
最常被列举的三支决策案例有两个:(1)论文的延迟录用;(2)医生的再诊断看病.二支决策对论文录用只取两种可能性,录用和不录用;三支决策则有三种可能性:录用、待定和不录用.三支决策的优点是可以减少决策的失误,使决策更合理.对于那些要求最终决策是二分的,三支决策通过信息的再收集,对待定部分进行进一步的决策,从而使最终的二支决策更合理.如:对待定论文的格式、语法等要求修改,修改后再做决策,可以使一些具有优秀思想的论文不被遗漏.
三支决策在国内和国际上已有许多大学和研究机构在深入开展工作,在国内如:南京大学、西南交通大学、同济大学、闽南师范大学、上海师范大学等,国际上姚一豫教授所在的加拿大University of Regina是研究主力,2013年7月国内出版了《三支决策与粒计算》一书,全面地介绍了三支决策方面的国内外研究动向.
“马云成功”案例是又一个三支决策典型案例,因为马云是许多创业年轻人的偶像,所以分析马云案例具有重要价值.本文作者对“马云成功”案例进行了分析和数学建模,并举一反三分析了“货币的起源”和“中庸之道”决策思想,从中可以看到三支决策是人类处理不确定性问题普遍采用的有效方法,也说明了系统研究三支决策理论及应用的重要性.
1 集合论与三支决策理论
Cantor集合边界为空,BND(X)=φ,Zadeh集合边界非空,BND(X)≠φ,这是两种集合的本质区别.模糊集理论和粗糙集理论给出了两种不同的对边界非空集合的刻画理论,模糊集理论对边界的刻画采用直接方法,粗糙集理论对边界的刻画采用间接方法,可以创造出无数种边界刻画方法和理论.人们已经有模糊粗糙集、粗糙模糊集、概率粗糙集、0.5概率粗糙集、随机集、区间集、云模型、II型模糊集、广义粗糙集、阴影集、灰度集等等理论,这些由概念的排列组合创造的新理论存在等价或部分等价性,显然需要理论的融合和归类.
二支决策是指决策的结果只有两种可能性:肯定或否定,它们对应的逻辑真值为1或0.三支决策是指决策的结果有3种可能性:肯定、不确定、否定,对应的逻辑真值为1、(0,1)、0,其中的不确定部分又可看成是“不决策”或“延迟决策”部分,因为这部分中的对象最终是划入肯定或否定,需要进一步的决策信息.三支决策方法是人类处理不确定性问题时常用的代价较小的有效方法.三支决策理论的形成是从粗糙集理论、决策粗糙集理论、三支决策理论一路演化而来,下面分别说明各理论的主旨思想.
1.1 粗糙集理论与决策粗糙集理论
Rough set是波兰数学家Z.Pawlak 1982年提出的一种刻画边界非空集合的理论,和模糊集理论不同,它采用间接刻画边界的方法,用两个分明的上下近似集合,限定了边界的范围.这种方法的最大优点是:用分类思想粗粒度地对概念进行定义,从而具有更广泛的适用性.分类思想贯穿了粗糙集理论的全部,因为分类是人类认识外部世界的主要方法,所以粗糙集理论获得了广泛的应用.
在信息系统S上定义粗糙集X,假设粗糙集X为目标概念,[x]R为U上含x的等价类,用等价类的并集作上下近似集去近似逼近粗糙集X,也同时定义了粗糙集X,令:
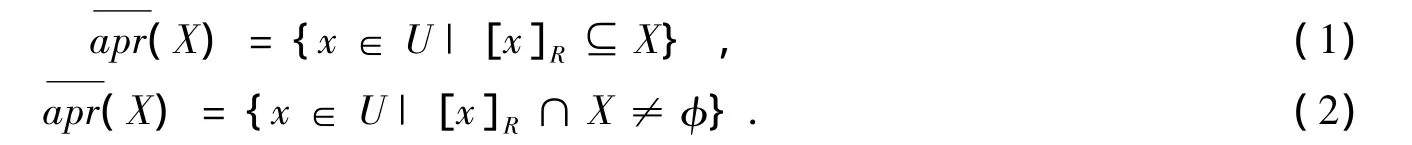
上下近似集同时给出了对论域的一个划分:
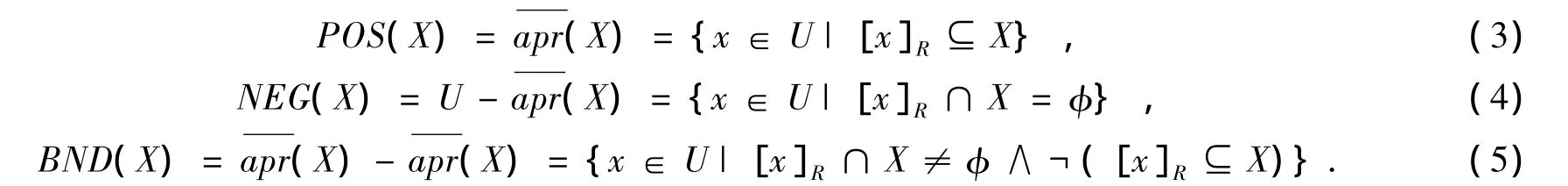
其中(3)为正域,(4)为负域,(5)为边界域.粗糙集对三个区域并没有做语义上的定义,在实际应用中给予语义定义可以使粗糙集应用于具体的问题求解,这也是三支决策和粗糙集相互关联的原因.
当从信息系统中获取知识时,立刻会碰到一个问题,对论域的划分的标准或方法是什么?粗糙集给出了分类思想,但并没有给出所有的分类方法,不同的分类方法对应获得知识的不同手段[12-13].Bayes决策论给出了基于概率分布的风险最小分类方法,将这种方法与粗糙集结合,就产生了决策粗糙集理论.若单类决策的代价矩阵如表1所示.

表1 单类决策的代价矩阵
运用Bayes最小代价决策原理,得α,β:

三支决策判据为:
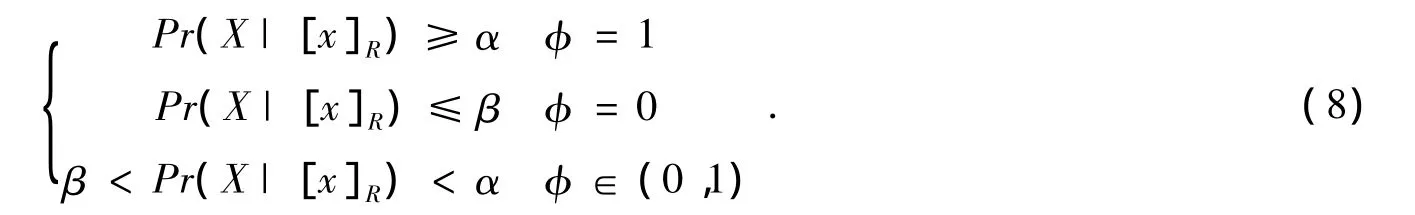
其中Pr(X|[x]R)为[x]R中对象属于X的概率,作为评价函数,通过(8)式获得代价最小决策的正域、负域和边界域,Pr(X|[x]R)可通过朴素 Bayes粗糙集方法求得[17-20].
1.2 三支决策理论
关于三支决策理论存在这样两个问题:(1)三支决策和粗糙集的关系?(2)三支决策理论是怎样的一种理论?
从姚一豫教授的文献看,三支决策思想来源于对粗糙集正域、负域、边界域语义解释的思考.所以三支决策理论应该是来源于对粗糙集理论的研究,但三支决策作为一种方法早已被人们使用过,只是在不自觉中,没有理论指导情况下使用.就三支决策和粗糙集的相关性而言,似乎两者没有必然的蕴涵关系,而更像是一种并列关系,也就是三支决策可以和任何与它相关的理论结合产生新思想.
这样就产生了三支决策理论到底是怎样一种理论的问题?从众多实例可以看到,在1965年L.A.Zadeh博士提出fuzzy set之前,人类早就有了处理不确定性问题,除了概率方法外,三支决策方法是所有处理不确定性问题中代价较小的方法,所以从这个角度考虑,三支决策理论应该是一种处理不确定性问题的代价较小的有效数学方法.
设(L,≤)是一个全序关系集,其中≤是全序关系,即≤具有自反、反对称和传递关系,且集合L中任意2个元素是可比较的,≤是一个小于等于关系.基于全序关系及一对阈值,可定义以下三支决策模型.
定义:设(L,≤)是一个全序集,其中≤是一个全序关系,α,β是满足条件β<α的2个元素,集合L+={t∈L|t≥α}表示指定接受值区,集合L-={b∈L|b≤β}表示指定拒绝值区.给定评价函数v:U→L,三支决策可以定义为:
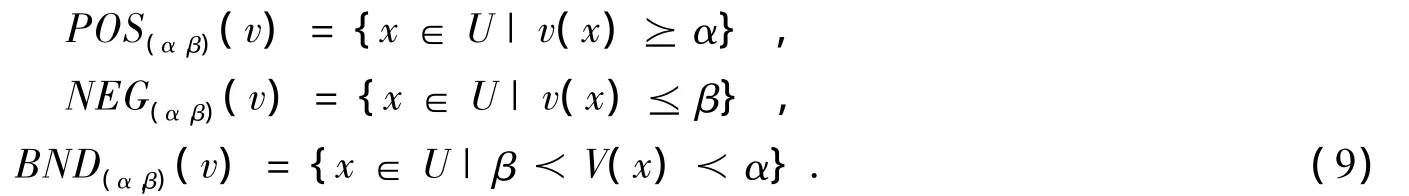
以上模型从评价函数应该遵循的代数序结构广义地定义了三支决策概念.三支决策理论和粗糙集理论最主要的不同是存在再决策机制,粗糙集理论由于对正域、负域和边界域没有赋予语义,所以也就不存在再决策问题,而三支决策赋予边界待定决策的语义,所以就存在对边界的进一步刻画问题.三支决策的再决策和粗糙集的属性约简有相同的作用,粗糙集的属性约简是在决策属性中对分类无效的属性的剔除,而三支决策首先选择最重要决策属性对论域进行粗分类,在获得边界域后,再选择属性对边界进行细分类,依此类推直到获得满意结果.三支决策的这种分类思想实际上就是粒计算由粗到细的分析方法,这种方法在一些具体问题中比直接的属性约简效率更高.
2 马云成功的三支决策案例分析与建模
传统交易是一手交钱一手交货,所以支付决策只需要二支的,即:支付或不支付.但电子商务存在空间和时间距离,不能实现一手交钱一手交货,这样就存在电子商务二支支付决策的风险问题:如果客户在网上订货后立刻支付,会面临商家不发货或发货不符合要求的风险;如果客户订货后不支付,风险留给了商家,商家也不发货,完成不了交易.所以二支支付决策不适合电子商务.马云正是看到了这一点,马云所做的是帮助客户实现了三支决策,即增加了“延迟支付”.这样有效地减少了客户的交易风险,也帮助商家实现了网上销售.
马云做到这一点所使用的方法,就是通常所说的做老娘舅,客户订货后首先将货款打入支付宝,支付宝收到货款后通知商家发货,客户收到货物后检查确认,通知支付宝,支付宝再将货款打给商家,完成交易.马云还建立了客户损失的先赔付制度,先赔付可能会有损失,但不良商家毕竟是少数,从概率计算获得的信誉大于损失,这样就将客户交易风险降到了最低,实现了一个成功的商业模式.
可能马云当时设计商业模式时,并没有意识到他所使用的是将支付二支决策改成三支决策,但他实际实现的就是提供“延迟支付服务”,让客户从传统的支付或不支付决策,变成支付、不支付、待定支付的三支决策.对待定支付通过交易过程中提供的更多信息,最后决定是否支付.当然如果客户和商家已有充分的信任,直接支付或不支付也可以,毕竟马云提供的服务是要收份子钱的.
能否通过对马云案例的分析,给出一个数学模型,以便所有的人在他们所在的专业或行业进行马云案例的复制,这是一个非常值得研究的问题.首先这是一个决策问题,在生活和工作中人人都要做决策.马云成功案例是将一个古老的二支决策,因为交易环境的改变,由原来的当面交易变成网络交易,而不再适用改成了三支决策.当二支决策改成三支决策后会多出许多工作,马云将其变成“服务”,当然提供服务不是无偿的,从中就形成了新的商业模式.如果考虑更复杂的情况,如:大数据中的数据挖掘,将原来的二支决策分类改成三支决策分类,并由计算机自动完成,这时就需要建立适当的数学模型.
马云案例中的相关要素是:(1)存在一个传统的二支决策,最终决策也要求是二分的;(2)由于决策的条件、环境改变或需要决策最优化,原二支决策不再适用或非最优;(3)将二支决策改为三支决策,其中的待定部分需要进一步的信息,以便进行再决策,获得这些信息需要新方法或新服务,从中得到创新思想或创新商业模式;(4)如果一层三支决策不满足要求可进行多层三支决策,直到满足需要的最终二支决策精度.根据上述要素可给出马云案例的一个数学模型.
(1)首先建立决策对象系统,也称信息系统S,包括4个集合:U,A,D,I.
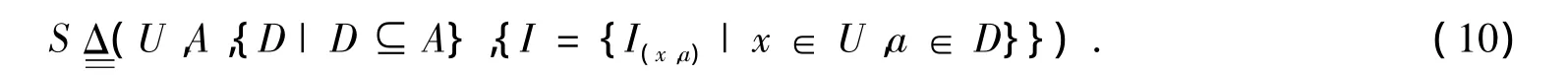
其中U为对象论域,任何决策都存在决策的客观主体,在马云案例中为已订购的货物,论文录用案例中是投稿论文,看病诊断案例中是就诊者;A为对象的所有属性集合,人类认识事物总是通过属性进行的,如认识一个人总是通过他的相貌、性格、习惯等属性去认识,原则上说对象的属性是无限多的,在实际问题中只取用到的属性;D为决策属性,是决策中用到的所有属性,包括条件属性和它们组合决定的属性.具体的决策,总是可以等价为根据某些属性对对象归属类的划分,如马云案例中,对已定货物的交易属性进行划分,付款或不付款.对对象集刻画的精度取决于独立属性集的势,一般来说要提高分类精度就必须将更多的属性作为决策属性,即D⊂D′;I为决策属性的映射量化值集,在马云案例中,可为交易的风险.
(2)在信息系统S上存在一个传统的二支决策问题,如马云案例中的支付决策,即:

其中φ为决策逻辑值,1对应正域,0对应负域,正负域均为分明集;α为决策阈值.
(3)假设决策条件、环境改变,或需要更优决策,原二支决策不能满足要求,现改为三支决策.即:

其中φ为决策逻辑值,1对应正域,0对应负域,(0,1)对应边界域,正负域和边界域均为分明集;(α,β)为决策阈值对.
(4)要对步骤(3)中的边界域进一步决策,需要信息,也即需要增加新决策属性,信息系统变为:
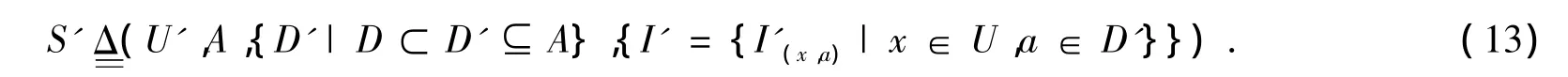
其中U′为步骤(3)获得的边界域;A为边界域中元素的所有属性;D′为新决策属性集;I′新属性的映射值域.对系统(13)再进行二支决策或三支决策,如本次二支决策已满足要求就只进行二支决策,并结束程序;如本次二支决策不满足要求,则仍运用三支决策.
(5)对仍需三支决策的系统继续使用三支决策,直至满足要求的二分精度.这样就构成了一个三支决策序列:

其中SD1SD2…SDn-1为三支决策,最后的决策SDn为二支决策,并得出结果,中止程序.其中的决策阈值对(α,β)可由三支决策粗糙集理论给出.
3 基于三支决策的商业模式设计
运用上述模型复制马云案例的商业模式设计.取3个不太相关的名词:体育官员、商业模式、三支决策.设想体育官员是某奥运主办国的组委会主席,或国际泳联主席,他或她想设计一个商业模式帮助体育赛事成功,毕竟谁都不想做赔本的买卖,方法是运用上述模型复制马云成功案例.
步骤1:找一个传统的二支决策.体育比赛中有许多项目是通过打分来决定胜负的,如:花样游泳、跳水比赛、体操比赛等.裁判员给运动员A、B打分,分高者胜出,这可以看成是一个二支决策,即:{winner|A>B,loser|A<B},但裁判打分有时也会出现分数相同的情况,即A=B,这时传统的处理方法是将运动员名次并列.体育比赛的宗旨是通过胜负来激励上进,并列名次不是最优选择,这样就可以考虑使用三支决策了.在这个例子中,给出的论域是所有参赛运动员U={所有参赛运动员},决策属性集为运动员的比赛成绩D={比赛成绩},决策属性的量化值集为裁判打的分数I={裁判打分}.
步骤2:决策优化.这是寻找新商业模式的动因.裁判给出相同的分数,说明裁判无法判断A、B的胜负,这相当于三支决策中的待定决策.如果要对待定的情况进一步做出判决,就需要新的信息,马云的成功实际上就是在新信息上做了文章,那么对体育比赛的相同分,能否也可在获得新信息上产生新的商业模式呢?
步骤3:运用三支决策.要对裁判打出的相同分作出进一步的决策,新信息已不能再从裁判那里来,有一个好的来源:观众,观众是体育比赛的组成部分,没有观众就没有体育比赛.观众来看体育比赛,尤其是打分类比赛,是来欣赏美的,观众也有权利对比赛做出自己的评判.所以可以在每位观众座位上安装一个打分器,当出现相同分数时,规定由观众打出的观赏分的高低决定运动员的胜负.这里对三支决策中边界域的再决策,使用的新属性量化值集是观众的打分I′={观众打分},根据观众打分完成决策.
这样做的代价:增加了打分设备.但现在的无线或有线打分设备非常普通和实用,从经济和技术上不存在什么问题.
这样做的好处:(1)提高了观众的参与积极性;(2)提高门票收入;(3)给了裁判员更多的选择余地;(4)使比赛更合理,更精彩.
代价和收益相比,收益远远大于代价,所以是一个可能的成功商业模式.
4 货币的起源与三支决策
运用马云案例来分析货币的起源及本质.商品交换的最初形式是易货交换,即:等价货物与等价货物的直接交换.例如1匹马换10头羊、1头猪换3头羊、1匹布换5个陶罐等等.但原始人类在产品交换时会碰到一个问题,当他有多余产品时却可能暂时没有他所需要的产品可交换,这时就产生了货币的需求,即:公认的等价交换物,比如羊,贵金属金、银等.首先与等价物交换,延迟易货交易,如果发现有人有他所需要的货物时,再用等价物去交换.原始货币是“公认的等价交换物”,起到的作用是延迟易货交易.从三支决策的角度看,就是将交易决策由原来的:易货交易和不易货交易的二支决策,改变成:易货交易、不易货交易、延迟易货交易的三支决策.实现延迟易货交易的方法就是使用货币,这样货币就产生了.
开始货币是有真实价值的等价物,如金银,但货币的作用就是证明产品价值的凭证,既然仅仅是一种凭证,凭证本身的价值就不重要了,这样纸币就产生了.因为纸币本身没有价值,所以需要有一定的信用作为担保,如商号信用,国家信用等.
网络时代的到来使货币又一次改变它的形态:存储器中的数字符号,产生了电子货币.一个亿万富翁可能一无所有,有的只是银行存储器中的1串数字,占有的空间肉眼都看不清.
因此从三支决策角度看,货币的本质是延迟商品交换的等价符号,有了这样的认识,就很容易理解大量的货币的货币的本质,如:股票、期货,货币衍生品等等.
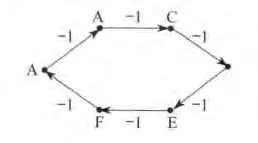
图1 封闭债务链
作为应用来考虑债务链的问题.商品交易中经常会出现债务,所谓债务链(如图1所示)就是A欠B一百万,B欠C一百万,C欠D一百万…,有时债务链会很长,但无论债务链有多长,只要债务链是封闭的,就可以在所有相关债务方同意的情况下,一次性销账,因为货币是符号,所以仅对符号的操作可以以最小的代价解决实际问题.但往往由于信息的不畅通,相关债务方并不知道存在封闭债务链,这样就可以产生一种新服务,依靠国家信誉,进行债务链的智能检索,一旦发现存在封闭债务链,就可以通知相关债务方,如获授权,就可以及时销账,使经营正常.通常情况下,债务链是不封闭,经济危机就是由于债务链的断裂,导致企业的连锁倒闭,员工失业产生的.显然债务链智能检索系统,可以预测经济运行状态,预防经济危机的发生.
5 中庸之道与三支决策
中庸之道是中国传统儒家思想的精髓之一,中庸之道本质上也是一种三支决策,但和上述马云案例略有不同.马云案例中三支决策是中间过渡态,要求最终结果是二支决策,而中庸之道将三支决策中的中间部分,即边界作为最终的输出.
世界充满矛盾,所以在对象的决策属性中充满相互对立的矛盾属性,如:[好,坏],[美,丑],[肯定,否定],[民主,独裁],[喜欢,不喜欢]等.将矛盾的两个对立面作为决策属性分类,可得到二支决策.如:将人分成好人和坏人,将画分成美和丑,将学生分成好学生和坏学生.中庸之道认为,世界上不存在绝对的事物,任何事物都可能同时存在矛盾对立面的两个方面,而不是只据其一,所以在做决策时,正确的方法是根据客观事实取中间部分作为决策结果,这就是中庸之道,又称中庸决策.
中庸之道是一个纯社会科学理念,从来没有定量化研究过,这里我们首先给出中庸之道的一种定量数学描述方法.
中庸之道决策思想可以用图2表示.
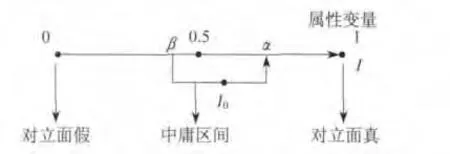
图2 中庸决策示意图
其中0,1表示矛盾的两个对立面,中间区间(α,β)表示中庸决策区间,如果决策信息足够完整,则中庸决策区间可缩小为一点I0,该点即为最优决策点;在信息不够充分的情况下,中庸决策区间宽度不为0,表明决策具有一定的不确定性,但不可能是两个极端点.
I为属性变量,用属性程度表示,定义:
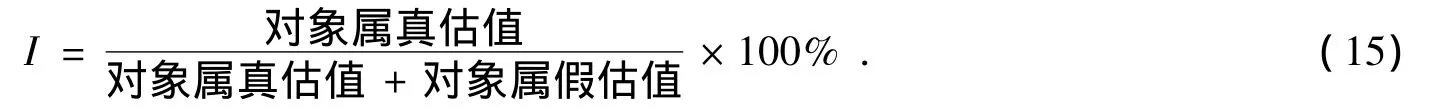
例如:一个国家经济成分中公有制固定资产为G+、私有制固定资产为G-,则一个国家的公有制程度I为:

对中庸决策区间(α,β)的估值可根据具体情况由数据统计计算得到,例如:对历史人物的评价,可以列出这个人物从生到死参与的所有重要事件ei,并按重要性排列{e1,e2,…,eN},重要性程度权重为wi∈[0,1],i=1,2,…,N.历史学家可以根据个人的判断对他所做事的好坏度进行评分 ei∈[0,1],i=1,2,…,N,根据评分和事件的重要性程度权重,用加权统计公式(17)可计算出已知事件的好坏决策点:

又根据对此人所作的未知事件的好坏估值得到评价误差ΔI,计算出评判者j对这个历史人物的中庸评判区间(α,I0,β)j|β=I0-ΔI≤I0≤α=I0+ΔI,最后对所有评判者的评判结果做区间统计平均得最终的评判结果:
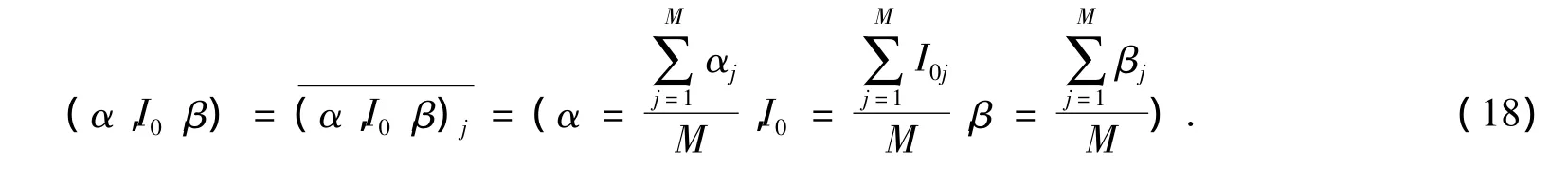
这样就可以对这个历史人物有一个数量上的相对客观的认识,如取(α,β)中的点I0得:3-7开或4-6开,前数表示不好的评价,后数表示好的评价.注意以前对历史人物的评价都是通过历史学家的脑袋主观进行的,现在可以用计算机进行一些辅助的工作了(如将历史人物做过的所有重要的事用计算机检索罗列出来,进行估值统计),这样可使评判更客观,这也是所讨论方法的意义.一个人只能是既有优点也有缺点,人与人之间的不同在于统计出的中庸评判区间不同,有人好事做得多一点,有人坏事做得多一点.图3是对历史人物评判的中庸决策图:
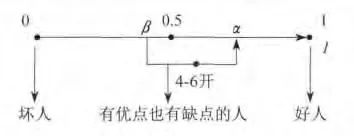
图3 用中庸决策对某历史人物做出的评价
中庸决策的关键是定位三支决策的边界区域,可以使用各种方法,上面介绍了加权统计法,另外还有如:模糊集的α截集逼近计算方法,粗糙集的上下近似集逼近方法等.
下面举两个运用中庸三支决策的例子:
例1:决策的民主化程度D与决策的合理性R之间的关系?如果要做一个决策,是发扬民主好还是独裁好?这个问题中的矛盾对立面是[绝对民主,绝对独裁].
首先考虑二支决策是否是最优的,也就是要么绝对民主,要么绝对独裁,显然二支决策对获得最合理的决策不是最优的.绝对独裁不是最优的例子很多,一个人的知识是有限的,世界上不存在一个对什么都能做出正确决策的人,所以发扬民主对合理决策是必要的;绝对民主也不是最优的,因为决策有时效性,民主决策是需要花时间的,如果在有效时效内决策不能完成,那么这个决策就是无效的.例如:打仗时一架飞机飞来,看不清是敌机还是友机,如果用绝对民主的方法来决策导弹打还是不打,那么也许敌机发起攻击时还没有完成决策,所以打仗时一般由长官来判断,而不是发扬民主.通常情况下,决策的合理性和决策的民主化程度之间存在一定的模糊函数关系R=F(D),其中D和R均为模糊数,这个函数关系由决策的环境和条件决定,并存在一个中间极值区间,这个区间对应的决策民主化程度就是最合理的,如图4所示.
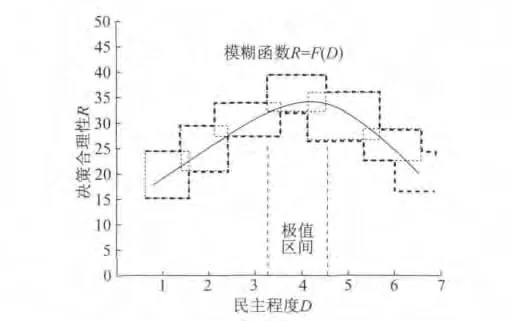
图4 决策的民主化程度与决策的合理性之间的模糊函数关系
例2:经济制度是绝对公有制好还是绝对私有制好?这个问题关系到一个国家全体人民的福祉,所以是非常重要的.公有制和私有制的选择历史上争论不休,甚至到今天也没有结论.这里用中庸三支决策的方法来分析这个问题.
该问题中的矛盾对立面是[绝对私有制,绝对公有制],首先来看看历史和现实中存在过的经济制度.美国是绝对私有制吗?不是,美国的原子弹也是公有的,如果原子弹也私有化那世界就离毁灭不远了.苏联是绝对公有制吗?也不是,至少个人的衣物是私有的.所以到目前为止,世界上存在的经济制度都不是绝对的公有制或绝对的私有制.这样就产生了一个经济制度中公有制成份和私有制成份比例为多少时是最优的问题?这个比例只能取决于当时国家的经济发展水平、生产力水平、人民的文明程度、自然资源情况等一系列主客观因素,这些因素决定了怎样的公有制成份比例是最优的.邓小平对中国的最大贡献就是他让中国选择了走中国特色的社会主义道路,也就是混合经济的道路.图5说明了中国特色的社会主义制度中的所有制的比例关系.
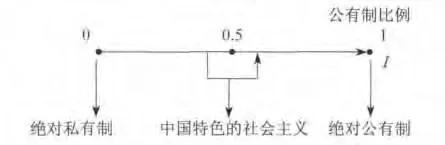
图5 中国特色的社会主义制度中的所有制比例关系
中国改革开放的成功使许多国家都希望向中国学习,也就是所谓的北京共识或北京模式,但如果从中庸之道看,北京共识的精髓恰恰是“不要照搬任何固有模式”,每个国家都有自己的条件和环境,只有根据自己的条件和环境决定自己的路才是最优的选择,这才是中国经验.
运用中庸之道做决策的例子很多,从以上例子可以看到,中华文明中的精髓不但过去有用,今天也有用,只是需要赋予新的内涵、新的解释.
6 总结
电子商务中马云的成功案例,货币的起源和本质,儒家哲学思想中的“中庸之道”这3个原本风马牛不相及的事却在三支决策中联系了起来,它们都是将同一种方法运用到不同方面得到的结果.从这里可以清楚地看到,三支决策方法是人类处理不确定性问题时经常采用的有效方法,研究三支决策理论及应用具有重要的意义.人类以往运用三支决策是不自觉的自发式的,一旦有了三支决策理论的指导就可以自觉地使用它,为人类创造出更多的合理的商业模式和人工智能方法.
[1]YAO Y Y,WONGSK M,Lingras PA.A decision theoretic rough set model:Proceedings of the5th International Symposium on Methodologies for Intelligent Systems[C].New York:North-Holland,1990.
[2]YAO Y Y.Three-way decision:An interpretation of rules in rough set theory:Proceedings of the 4th International Conference on Rough Sets and Knowledge Technology[C].Berlin-Verlag:Springer,2009.
[3]PAWLAK Z.Rough sets[J].International Journal of Computer and Information Sciences,1982,11:341-356.
[4]PAWLAK Z.Rough sets:Theoretical Aspects of Reasoning about Data[M].Norwell:Kluwer Academic Publishers,1991.
[5]ZHANG L,ZHANG B.Fuzzy quotient spaces(fuzzy granular computing approaches)[J].Chin J Soft,2003,14:770-776.
[6]YAO Y Y.Three-way decisions with probabilistic rough sets[J].Information Sciences,2010,180:341-353.
[7]LIU D,LI T R,LI H X.A multiple-category classification approach with decision-theoretic rough sets[J].Fundamenta Informaticae 2012,115:173-188.
[8]YAO Y Y.An outline of a theory of three-way decisions:Proceedings of the 8th international RSCTCconference[C].Berlin:Springer-Verlag,2012.
[9]ZHANG L,ZHANG B.The theory and application of tolerance relations[J].Int JGranular Compu,Rough Sets Intell Syst,2009,1:179-189.
[10]ZHANG L,ZHANG B.The structural analysis of fuzzy sets[J].Int J Approx Reason,2005,40:92-108.
[11]HERBERT J P,YAO J T.Game-theoretic rough sets[J].Fundamenta Informaticae 2011,108:267-286.
[12]CHENG Y,MIAO D Q,FENG QR.Positive approximation and converse approximation in interval-valued fuzzy rough sets[J].Information Sciences,2011,181(11):2086-2110.
[13]MIAO D Q,GAO C,ZHANG N,et al.Diverse reduct subspaces based co-training for partially labeled data[J].International Journal of Approximate Reasoning,2011,52(8):1103-1117.
[14]WANG G Y.Attribute Core of Decision Table[C]//ALPIGINI J J,PETERS J F,SKOWRON A,et al.Rough Sets and Current Trends in Computing.LNAI 2475,Berlin:Springer-Verlag,2002.
[15]LIU D,YAO Y Y,LI T R.Three-way investment decisions with decision-theoretic rough sets[J].International Journal of Computational Intelligence Systems,2011,4:66-74.
[16]LI Y F,ZHANG CQ,SWANB JR.An information filtering on the Web and its application in JobAgent[J].Knowledgebased Systems,2000,13:285-296.
[17]JIA X Y,LI X Y,LI W W,et al.An adaptive algorithm of solving the decision threshold in three-way decisions[J].Journal of Electronics(China),2011,11:2521-2525.
[18]JIA X Y,SHANG L,CHEN JJ.Decision-making risk minimization attribute reduction[J].Journal of Frontiers of Computer Science and Technology,2011,5:155-160.
[19]LI H X,LIU D,ZHOU X Z.Research summary for the decision-making rough set model[J].Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition,2012,22:624-630.
[20]LIU D,YAO Y Y,LI T R.Rough set three-way decisions[J].Computer Science,2011,38:245-250.
[21]YAO Y Y.Two semantic issues in a probabilistic rough set model[J].Fundamenta Informaticae ,2011,108:249-265.
[22]AZAM N,YAO JT.Multiple criteria decision analysis with game-theoretic rough sets:Proceedings of the 8th International RSCTCconference[C].Berlin:Springer-Verlag,2012.
[23]GRZYMALA-BUSSE J W.Generalized parameterized approximations:Proceedings of the 6th International conference on Rough Sets and Knowledge Technology LNCS(LNAI)6954[C].Berlin:Springer-Verlag,2011.
[24]GRZYMALA-BUSSE JW,YAO Y Y.Probabilistic rule induction with the LERS data mining system[J].International Journal of Intelligent Systems,2011,26:518-539.
[25]HERBERT J P,YAO J T.Learning optimal parameters in decision-theoretic rough sets:Proceedings of the 4th International Conference on Rough Sets and Knowledge Technology LNCS(LNAI)5589[C].Berlin:Springer-Verlag,2009.
[26]HERBERT J P,YAO J T.Analysis of Data-Driven Parameters in Game-Theoretic Rough Sets[C]//YAO J,RAMANNA S,WANG G,et al.RSKT 2011.LNCS(LNAI),Berlin:Springer-Verlag,2011.
[27]WOODWARD P W,NAYLOR J C.An application of Bayesian methods in SPC[J].The Statistician,1993,42:461-469.
[28]YANG X P,SONG H G,LI T J.Decision Making in Incomplete Information System Based on Decision-Theoretic Rough Sets[C]//YAO J,RAMANNA S,WANG G,et al.ZRSKT 2011.LNCS(LNAI),Berlin:Springer-Verlag,2011.
[29]YANG X P,YAO JT.Modelling multi-agent three-way decisions with decision theoretic rough sets[J].Fundamenta Informaticae,2012,115:157-171 .
[30]YAO Y Y.Interval-set algebra for qualitative knowledge representation:Proceedings of the 5th International Conference on Computing and Information[C].Ontario:IEEE,1993.
