统一潮流控制器潮流模型及功率调节能力分析
2015-10-24郑华,高芬
郑 华,高 芬
(华北电力大学电气与电子工程学院,北京 102206)
统一潮流控制器潮流模型及功率调节能力分析
郑 华,高 芬
(华北电力大学电气与电子工程学院,北京 102206)
随着电网规模和交直流混合系统建设工作的快速推进,UPEC应用研究又成为热点之一。针对UPEC的不同控制需要,开展了不同控制策略下UPEC控制特性分析及其对电网潮流的影响研究。首先,本文针对不同的UPEC控制策略,建立了相应的常规潮流方程的修改模型,实现了直接采用常规潮流程序计算含UPEC的电网潮流的方法;然后,通过含UPEC电网的潮流分析,剖析了UPEC的稳态调控性能及其对系统潮流的影响能力;最后通过典型数据验证了本文模型和方法的有效性,对实际电网中应用UPEC具有一定的借鉴与指导意义。
UPEC;控制特性;潮流计算模型;潮流调节能力
0 引 言
EACTS的概念诞生于20世纪80年代末,它的出现对电力系统安全、可靠、经济和优质运行提供了有效手段。EACTS技术自提出后就得到了迅速的发展和推广,成为电力工业近20年来发展最快和影响最广泛的新型技术领域之一,目前已有很多EACTS控制器如SVC、TCSC、STATCOM等投入实际运行,并在电力系统中发挥着越来越重要的作用[1]。统一潮流控制器(UPEC)作为第三代EACTS控制器,集串联补偿、并联补偿、移相等控制功能为一体,已成为目前最具有影响力的控制器之一。
目前国内外许多学者在计及UPEC的潮流计算方面进行了许多工作,在一定程度上解决了含UPEC的电力系统潮流计算问题[2]。含UPEC的电力系统潮流主要有两种求解思路:一种是直接求解非线性方程法(解析法),但当UPEC控制变量被选作新增状态变量时,初始值的选取有一定的难度,现在还没有一个比较成熟的公式或经验值,常常造成潮流计算的发散或振荡而不收敛,另外如何尽量减少新增状态量和方程维数也是该方法的一个重点研究内容;另一种思路是网络等值求解,最常用的是等效附加注入功率法(功率注入法),但该模型的通用性较差,只适合于UPEC的串联变换器采用手动电压注入模式下的潮流计算,且并未考虑并联变换器不同控制模式的影响。这些研究均是为了解决UPEC在某种特定控制功能下的潮流计算问题,而从全局控制策略角度出发,尚缺乏系统归纳和通用处理模型方面的研究。
本文首先针对含UPEC的电力系统潮流计算问题进行分析,分析UPEC的具体功能和所有可能的控制策略,提出了不同的潮流模型,从常规潮流方程出发,推导出不同控制策略下的含UPEC电网潮流求解算法,构建了含UPEC的潮流计算通用处理步骤和模型,并进行了潮流计算性能的对比分析。最后,结合IEEE经典算例,剖析了UPEC对系统电压及功率的调节性能,验证了UPEC的强大控制特性及其能力。
1 UPFC稳态模型及潮流计算
统一潮流控制器(UPEC)的主电路由两个换流器组成,换流器1通过变压器T1并联接入系统,换流器2通过变压器T2串联接入系统,两个换流器通过共用的直流电容相连,如图1所示。这种背靠背式的交流-交流的电力转换器可以实现有功功率的自由流通,而且这两个换流器可以在自己的交流端上独立产生(或吸收)无功功率,因而UPEC内部仅有有功功率的流通。正是UPEC这种独特的组成结构,决定了它可以同时具有并联补偿和串联补偿的功能。
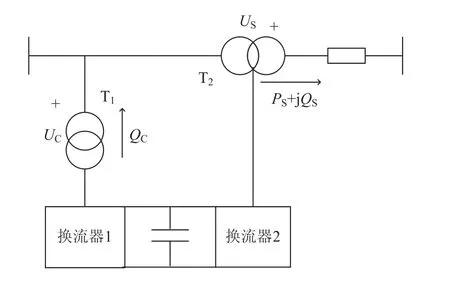
图1 UPEC原理图
含UPEC的电力系统潮流计算流程如图2所示,其一般步骤如下:
第一步,根据UPEC的具体功能和系统运行的需要给出控制变量。
表1中,UC、QC分别表示并联变换器通过变压器T1并联接入系统的电压和并联注入无功功率,US、PS+QS分别表示串联变换器通过变压器T2串联接入系统的电压和控制的支路功率,如图1所示。

表1 UPFC功能与控制变量
表1中可以看出,UPEC串联、并联部分各有两种控制模式,串、并联可以有4种控制模式的组合:电压调节和电压注入,无功控制和电压注入,电压调节和功率控制,无功控制和功率控制。
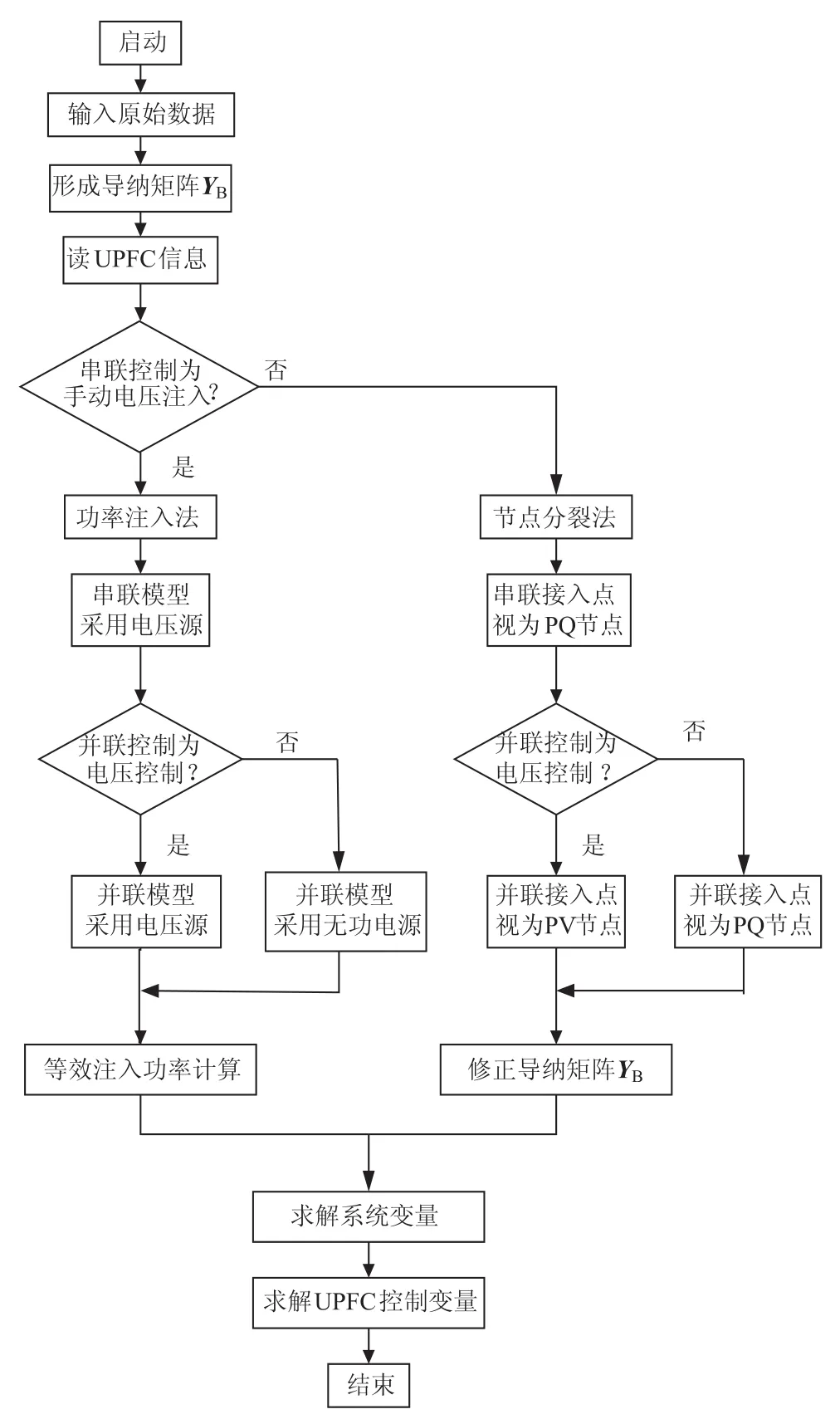
图2 含UPEC潮流计算流程图
第二步,建立合适的模型,采用合适的算法。
UPEC并联部分的主要功能是维持UPEC接入点电压值以及共用电容上的直流电压值,从而实现有功功率的传递,UPEC最主要的潮流控制功能是由串联部分实现的。从表2中也可以看出含UPEC的电力系统潮流算法的选择也主要是根据串联模型而定。

表2 UPFC潮流模型与算法
当串联变换器采用电压注入模式时,相当于在系统支路中引入了串联电压源,改变了原有电力网络无源特性的特征,一般采用功率注入法将串联电压源效应转移到所在线路的两个节点上;当串联变换器采用功率注入模式时,相当于给出了UPEC后接入点为潮流计算中的PQ节点条件,潮流计算采用节点分裂法,通过简单修改雅克比矩阵计算系统潮流。
第三步,计算出系统的状态变量和UPEC的控制变量。
1.1模型一
在电压调节和电压注入模式下UPEC模型分别等效为串联电压源和并联电压源的组合,如图3(a)所示。
通常,在不增加网络维数和不定参量的情况下,为了将UPEC串入电网的电压源附加效应等效,通常采用功率注入法其转化为对两端节点的等效附加注入功率形式,如图3(b)所示。
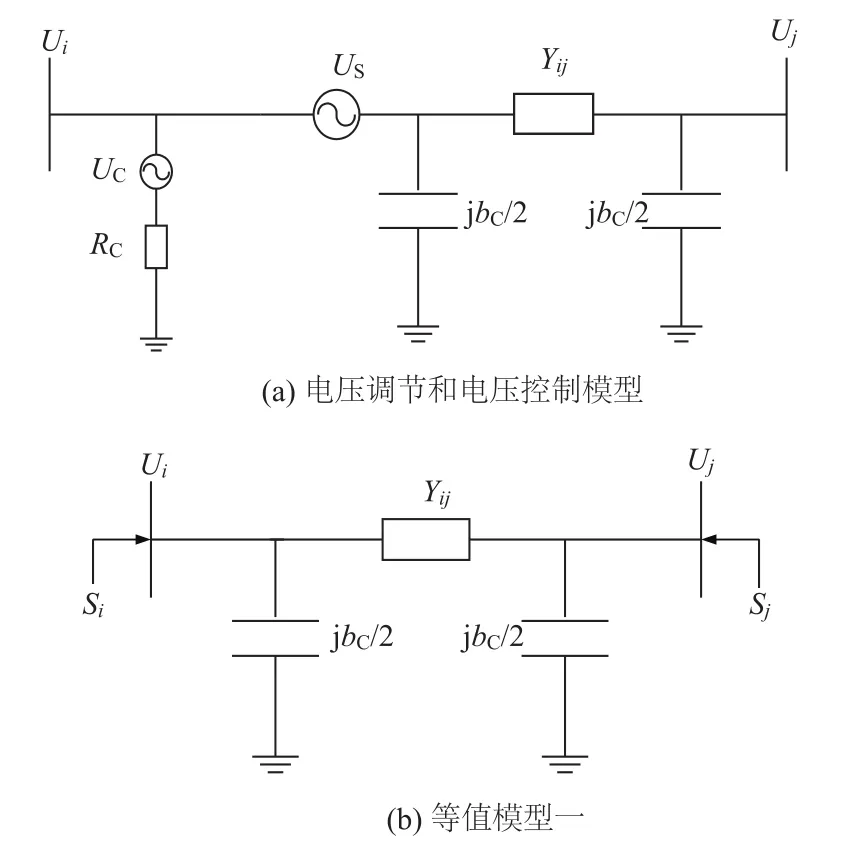
图3 UPEC潮流模型一
根据功率注入法,UPEC模型可以表示为
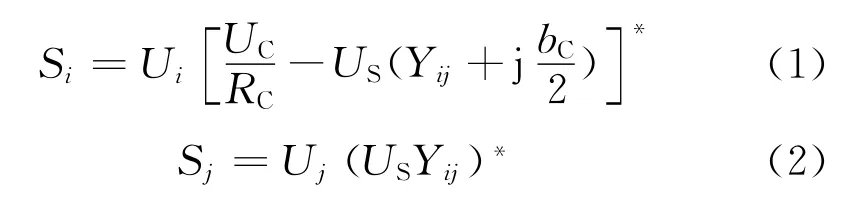
以及附加的等式约束条件:
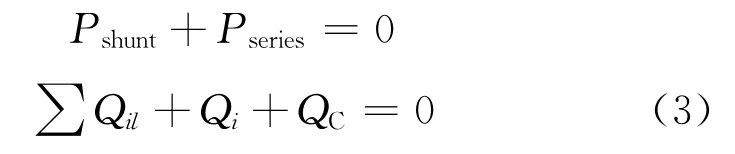
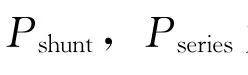
在常规潮流计算程序中,在原功率列向量的i、j行元素的基础上增加式(1)、式(2)得出的附加注入功率,如式(4)所示,然后就可以用修改后的常规潮流程序进行含UPEC的电力系统潮流计算,得出系统状态变量。
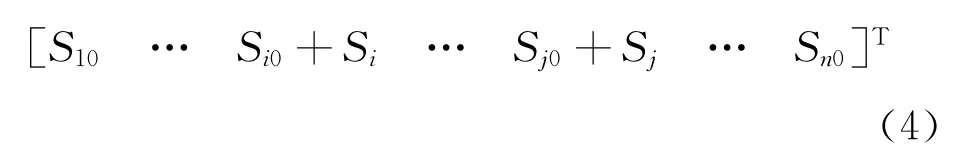
1.2模型二
表2表明,在无功控制和电压注入模式下,含UPEC的潮流算法采用功率注入法,与电压调节和电压控制模式不同的是并联采用无功电源模型等效UPEC的无功控制能力,串联模型仍采用串联电压源,如图4(a)所示。
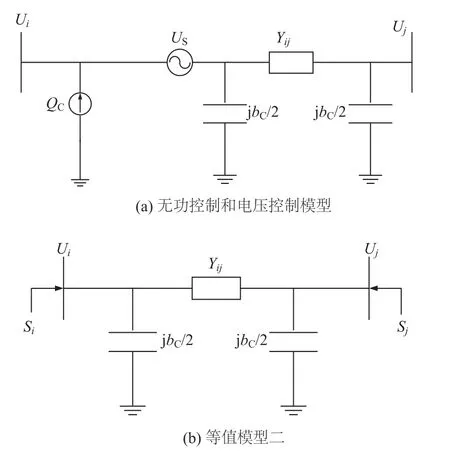
图4 UPEC潮流模型二
根据功率注入法,此时的UPEC模型表示为
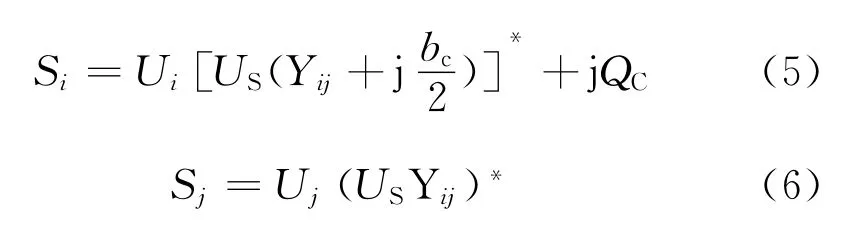
附加的等式约束条件与式(3)相同。
同样的,在常规潮流计算程序中,在原功率列向量的i、j行元素的基础上增加UPEC附加注入功率,进而计算含UPEC的电力系统潮流计算。
1.3 模型三
在电压调节和功率控制模式下,UPEC传统意义上的控制目标(线路潮流)则变为了控制参量,此时虽然可以通过解非线性方程组进行潮流计算,但这种求解方法计算时间长,对初值的要求较高且收敛性差。
考虑到UPEC元件的控制特性,如图5(a)所示,在电压调节和功率控制的控制策略下,UPEC接入点电压Ui可控,UPEC后支路潮流PS、QS可控,因此可以把UPEC所在位置分裂为两个节点i和i′,分别可以视为PV节点和PQ节点,如图5(b)所示。
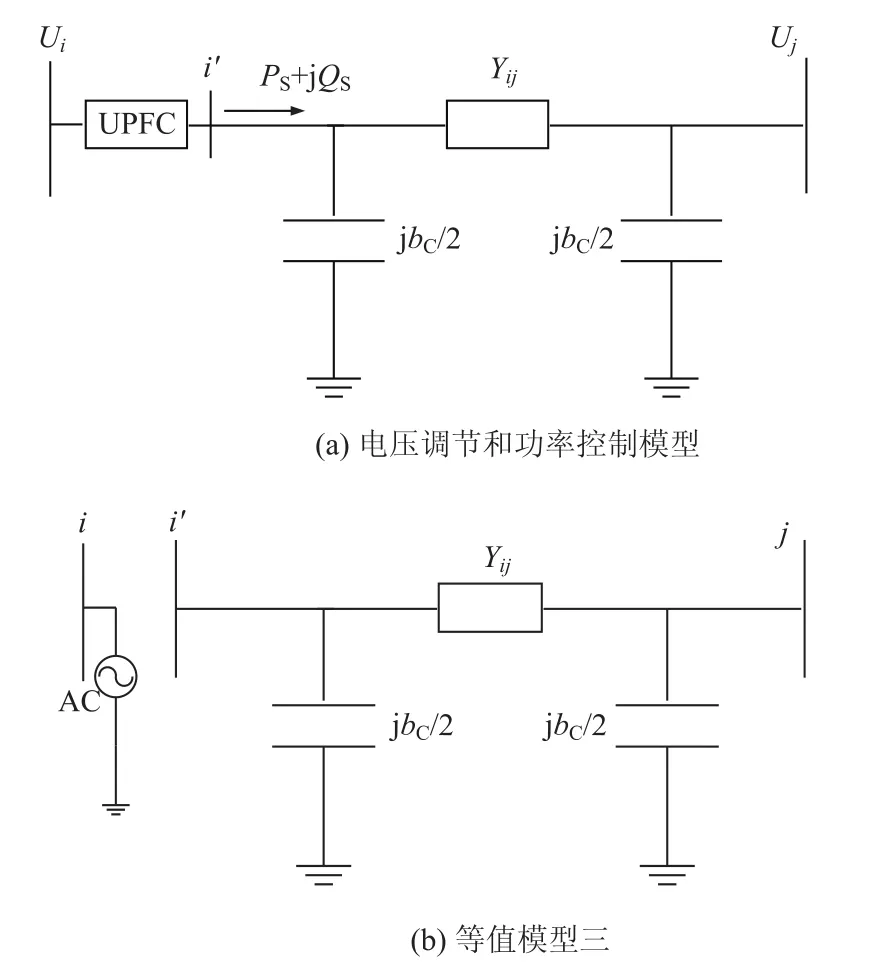
图5 UPEC潮流模型三
采用节点分裂的方法,UPEC所处位置分裂为两个节点,节点i与i′之间没有实际支路的连接,但存在功率和电压上的关联:
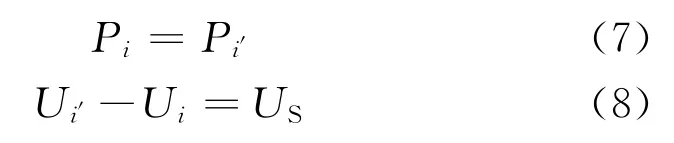
此外,由于节点分裂法额外增加了节点数目,相应的阻抗矩阵也需要修改。常规阻抗矩阵如式(9)所示需增加一行一列i′,单独拿出i、j之间的部分矩阵如式(10)所示,根据节点分裂法,需要对这部分矩阵做如下处理:由于节点i′作为节点i的分裂节点,只与j相连,因而式(10)中的小矩阵块变为式(11)中的i′与j的矩阵块,除了这4个元素外,i′行、i′列的其他元素均为0,节点i、j无连接关系,故相应位置元素变为0,节点i自阻抗需减去支路ij的阻抗,修改后的矩阵如式(11)所示。

通过对常规潮流程序中的阻抗矩阵做上述简单修改,便可以直接用来计算含UPEC的电网潮流。
根据公式(8)由系统状态变量求出UPEC的控制变量。
1.4模型四
在无功控制和功率控制模式下,含UPEC的潮流算法采用节点分裂法,与电压控制和功率控制模式不同的是UPEC所在点分裂为两个PQ节点,如图6所示。
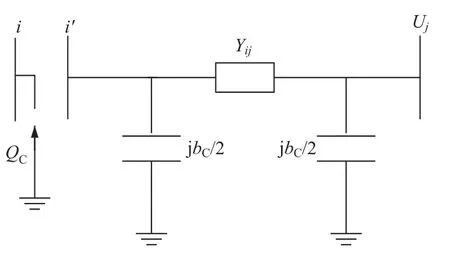
图6 UPEC潮流模型四
系统的原阻抗矩阵也需要做1.3节相同的处理,不同的是由于i节点视为PQ节点,潮流计算中少了i节点无功功率Q的计算,潮流程序并不需要做额外的修改。
同样的,潮流计算完成后,根据式(8)可由系统状态量求得UPEC控制量。
2 UPFC潮流计算及调节能力分析
2.1 潮流性能对比
将上述4种UPEC潮流模型应用在IEEE9、IEEE118和IEEE300标准系统中,UPEC分别装入3个系统中的7 8支路、27 32支路和37 40支路。
表3描述了3个标准测试系统的原始潮流计算时间以及基于UPEC的4种模型控制参数和潮流计算时间。并联参数分别表示:电压调节时,控制并联接入点电压为1.02p.u,无功控制时,注入无功为0.2p.u;串联参数表示:手动电压注入时,注入电压为线路电压的10%,功率控制时,功率改变量为原始功率的20%。
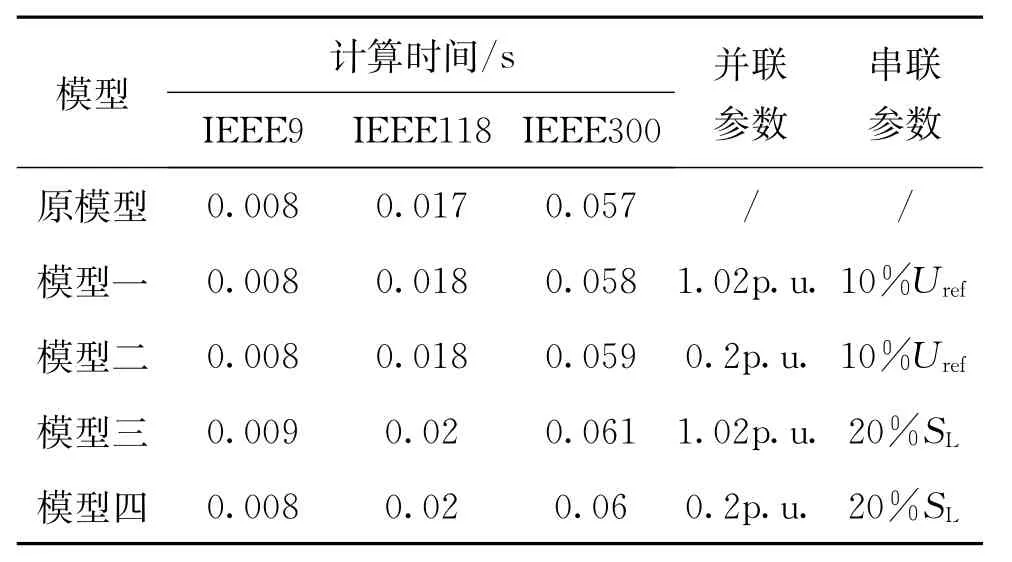
表3 含UPFC的潮流计算时间及控制参数
从表3中的数据可以看出,IEEE9节点系统原始潮流收敛时间为0.008s与含UPEC的IEEE9节点系统潮流收敛时间几乎相等;IEEE118节点系统原始潮流收敛时间为0.017s,含UPEC的IEEE118节点系统潮流在4种模型中最长收敛时间为0.02s,仅0.003s的差距;IEEE300节点系统收敛时间为0.057s,与最长收敛时间0.061s相差0.004s,具有300节点的系统时间仅增加了7%。因此应用本文所建的UPEC潮流控制模型,不仅可以实现含UPEC的电网潮流计算,且具有较快的计算速度。
2.2潮流调节能力分析
为了仿真系统搭建简单,便于验证分析,测试系统选用IEEE9节点系统,节点5、6、8为负荷点;节点2、3作为PV节点,节点1为平衡节点,如图7所示。由于系统是对称结构,且负荷点8处的负荷较重,因而,在支路7 8上安装UPEC装置,节点7为UPEC接入点。
2.2.1UPEC电压调节能力
通常认为UPEC的主要控制作用是由串联变换器实现的,但并联变换器在无功控制和电压调节两种不同控制策略下,UPEC对系统的控制作用也有所不同。
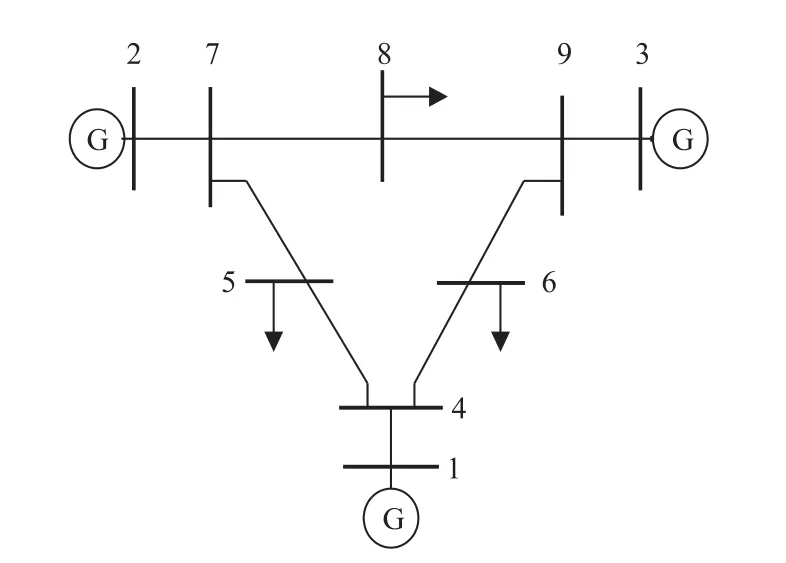
图7 IEEE9单线图

表4 系统未安装UPFC的初始电压值p.u.
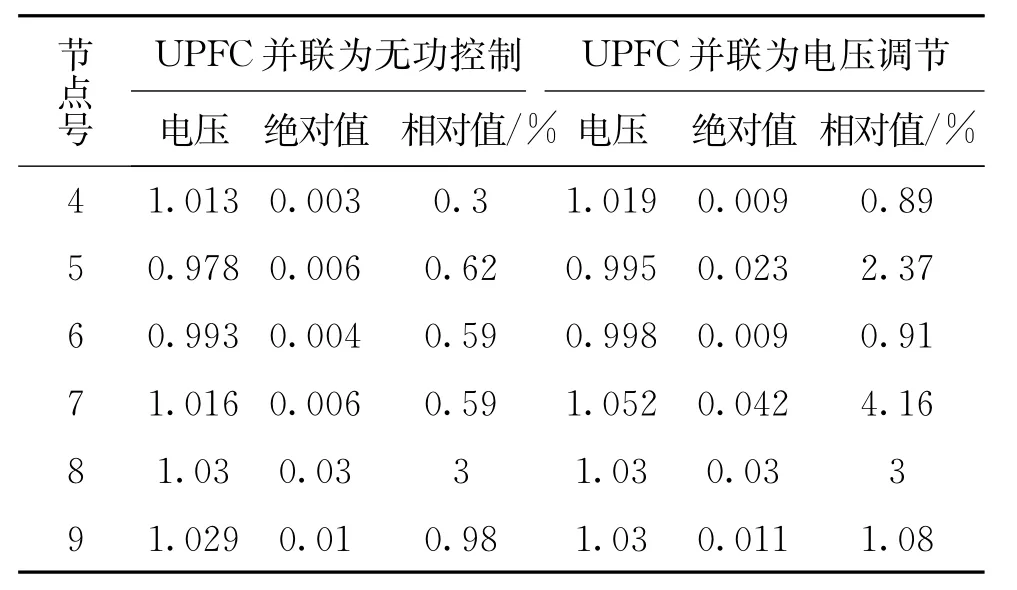
表5 安装UPFC后电压控制结果p.u.
表4给出了系统在无UPEC作用时的节点电压标幺值,表5给出了系统在含UPEC且并联变换器采用无功控制策略、含UPEC且并联变换器采用电压调节策略两种情况下的系统节点电压标幺值,由于节点1、2、3分别为平衡节点和PV节点,节点电压保持不变,表中并未列出。通过表格数据可以得出以下结论:
①负荷点5、6的节点电压较低,分别为0.972p.u、0.989p.u,在加入UPEC两种控制策略后,两个节点电压都有所增加,节点5的电压增加到0.978p.u和0.995p.u,分别增加了0.006p.u和0.023p.u;节点6的电压分别增加了0.004p.u和0.009p.u,系统其他节点的电压也均有所提高,可以看出,UPEC具有一定的电压调节能力。
②对比两种并联控制方式下的两列电压增加量,节点4在无功控制方式下电压增加0.297%,在电压调节控制方式下电压增加0.89%,后者多增加了0.593%,同样的,节点5、6、7、9在并联变换器处于电压调节控制方式下均比无功控制方式下电压增加量要多,分别多增加了1.75%、0.51%、3.57%和0.1%。上述数据说明,并联变换器采用电压调节策略比采用无功控制策略对电压的调节作用要强。
2.2.2UPEC潮流调控范围
本文中仿真系统并联部分维持接入电压幅值为1.02p.u.,主要讨论当给定串联电压幅值和相角时,线路潮流的变化特性。
图8为假定UC幅值最大为0.1,UC角度在0到360变化时各部分输出有功、无功的变化范围。图8所示最外的圆环代表UC幅值为0.1p.u.,向内依次递减0.02p.u.,从图中可见UPEC对线路潮流的控制范围是一系列的椭圆,椭圆的大小表示潮流控制能力的大小,说明UPEC在不同的方向上的调控能力也不同,适当调整UPEC的控制参数,可使线路功率达到椭圆内的任意值。
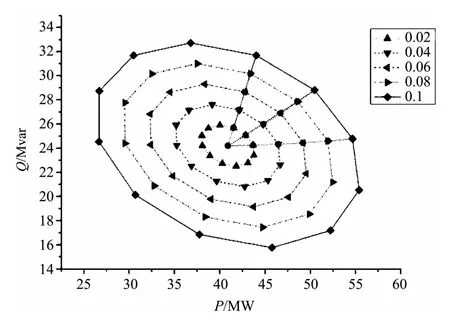
图8 P-Q运行范围
为了更直观地观察UPEC对支路潮流的控制能力,图9在三维空间中绘制了UPEC的控制范围,从图中可以很容易看出每一个P、Q点都只与控制曲面上的一个点对应,说明支路的P、Q值与UC、θ是一一对应的。
在三维空间中,UPEC的潮流控制范围表现为一个开口向上的圆锥体,开口的大小表示UPEC的调控能力,顶点表示该支路的原始功率(不含UPEC时),对比(a)图与(b)图可以看出,图(a)中的椭圆开口程度远大于图(b),即UPEC对支路7 8的调控能力远大于支路4 5,说明了UPEC对其所在的本地支路调控能力较系统其他的远方支路调控能力大,因此,支路距UPEC安装位置的电气距离也是影响UPEC控制能力的一个因素。
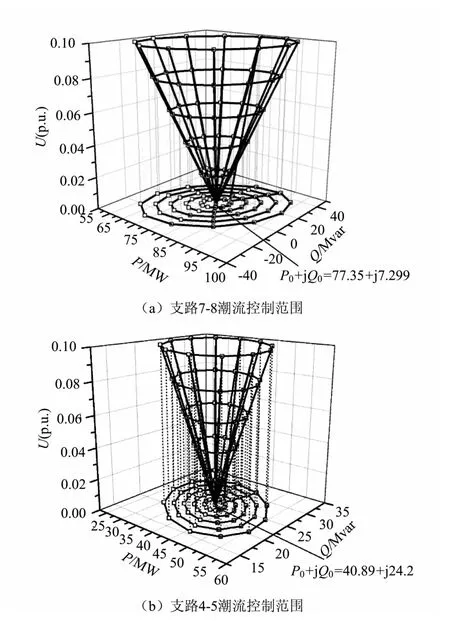
图9 UPEC潮流控制范围
此外,不管是二维图,还是三维图,我们都可以看出,在固定的θ方向上,随电压幅值的线性增加,功率也等比例的线性增加,二者存在线性关系。图10给出了在θ分别取0°、60°、180°、270°时支路7 8有功功率P与注入电压幅值U之间的关系,二者满足的关系为P=aU+b,其中b为直线截距,图中数值为77.32°,是该支路的初始功率;a为斜率,取值与θ有关。这也证明了用灵敏度等线性化方法分析UPEC控制能力以及多个UPEC共同作用时,控制能力可以线性叠加的可行性。
3 结 论
本文首先分析了含UPEC的电力系统潮流计算问题,构造了UPEC在多种控制策略下的潮流模型,从UPEC模型出发对潮流计算方法的选择和UPEC的等值处理进行详细阐述,推导出含UPEC的电网潮流的计算方法。算例表明,本文所建立的UPEC潮流模型可以快速完成含UPEC的电网的潮流求解。
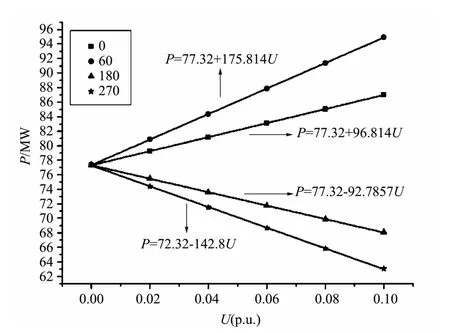
图10 P-V曲线图
针对UPEC对系统潮流调控能力问题,首先通过数据说明了UPEC对系统电压具有一定的调节能力,且并联控制策略采用电压调节时的电压调控能力比采用无功控制时要强。在分析UPEC对系统潮流的控制能力时,通过在二维空间和三维空间中的展示,表明了UPEC对线路潮流范围是一个椭圆,很小的串联注入电压便可以对线路功率产生很大的影响,其控制能力非常大,且与串联电压幅值呈线性关系。
[1] 颜伟,朱继忠.UPEC的潮流控制与暂态稳定性研究[J].中国电机工程学报,2000,20(12):57 61.
[2] 周玲,王宽,钱科军,等.计及UPEC的电力系统无功优化[J].中国电机工程学报,2008,28(4):37 41.
[3] 郭烨,张伯明,吴文传.节点类型扩展潮流计算及其可解性研究[J].中国电机工程学报,2011,31(13):79 85.
[4] Monticelli A,Garcia A,Saavedra O R.East decoupled load flow:hypothesis,derivations,and testing[J].IEEE Trans.on Power Systems,1990,PWRS 5(4):1425 1431.
[5] Behnam G K.East decoupled load flow:the hybrid model[J].IEEE Trans.on Power Systems,1989,PWRS 4(2):734 742.
[6] 顾伟,黄河,蒋平.用于三相电力系统潮流计算的UPEC稳态模型[J].高电压技术,2005,31(3):71 73.
[7] 李乃忠,叶鹏,张莉,等.基于网络等值的UPEC潮流计算研究[J].沈阳工程学院学报:自然科学版,2010(4):321 325.
[8] 王鲁.分解潮流收敛原理及新算法的研究[D].北京:清华大学,1989.
[9] 陈金富,段献忠.统一潮流控制器的静态潮流调节能力分析[J].清华大学学报:自然科学版,1999,39(3):92 95.
[10]杨慎飞.基于UPEC的配电网线路损耗控制研究[D].武汉:武汉理工大学,2012.
[11]Chang U C,Liu C C,Uang W T.Real-time line flow calculation using a new sensitivity method[J]. Electric Power System Research,1992,62(24):127 133.
[12]Komoni V,Krasniqi I,Kabashi G,et al.Control active and reactive power flow with UPEC connected in transmission line[C]//Power Generation,Transmission,Distribution and Energy Conversion(MEDPOWER 2012),8th Mediterranean Conference on. IET,2012:1 6.
[13]仉志华,徐丙垠,陈青.基于统一潮流控制器的配电环网潮流优化控制策略[J].电网技术,2012,36(6):122 126.
[14]刘前进,宋永华.基于功率注入法的UPEC潮流控制研究[J].清华大学学报:自然科学版,2001,41(3):55 58.
[15]罗春雷,孙洪波,徐国禹.含PQV节点的潮流计算在UPEC中的应用[J].电力系统自动化,1997,21(4):34 36.
[16]张伯明,陈寿孙,严正.高等电力网络分析[M]. 2版.北京:清华大学出版社,2007:69 80.
(责任编辑:林海文)
Analysis of Unified Power Flow Controller Model and Its Control Capability of Power Flow
ZHENG Hua,GAO Een
(School of Electrical and Electronic Engineering,North China Electric Power University,Beijing 102206,China)
With the increasing scale of power grid and construction of AC and DC hybrid system,the application of UPFC has become one of the key issues.In this paper,the control characteristics of UPFC under different control strategies and its influence on power flow are studied according to different control needs.Firstly,modified models of conventional power flow equations are built according to different UPFC control strategies,in which conventional power flow calculation program is used to calculate power flow with UPFC directly.Then,through analyzing the power flow with UPFC,the steady-state control performance of UPFC and its influence on power flow are analyzed.In the end,the validity of proposed model and the method are verified by classical data,which will have a certain reference and guiding significance for the application of UPFCin actual network.
UPFC;control characteristics;power flow calculation model;power flow control capability
1007-2322(2015)02-0043-07
A
TM74
2014-06-05
郑 华(1971—),男,博士,副教授,研究方向为智能电网运行与规划、高性能计算与可视化技术,E-mail:hbdl_ zhenghua@263.net;
高 芬(1989—),女,硕士研究生,研究方向为智能电网运行控制与优化,E-mail:fennijn@163.com。
