考虑复杂应变历史的钢材修正双曲面滞回模型

王 彤,谢 旭,唐站站,沈 赤2

（1.浙江大学建筑工程学院,浙江杭州310058；2.株式会社长大海外事业部,日本茨城305-0812）

考虑复杂应变历史的钢材修正双曲面滞回模型

王 彤1,谢 旭1,唐站站1,沈 赤2

（1.浙江大学建筑工程学院,浙江杭州310058；2.株式会社长大海外事业部,日本茨城305-0812）

针对兼顾精度和计算效率的钢材弹塑性滞回本构模型——修正双曲面模型在复杂应变历史条件下,由于弹-塑性过渡时塑性模量无穷大导致的应力计算结果不合理的缺陷,通过改进应力-应变路径的判别准则,对既有修正双曲面模型进行再修正,分别给出单轴应力状态和三维应力状态下的改进方法.通过与钢材单轴拉压试验结果的对比以及一系列相关算例的对比分析,证明了采用经改进后的双曲面滞回模型能够精确地模拟钢材在复杂应变历史条件下的滞回特性,从材料和结构构件2个层面验证了该改进方法的准确性和适用性.结果表明,对既有修正双曲面模型的改进能够有效地提高模型在复杂应变历史下的应力计算精度.

修正双曲面滞回模型；钢材；循环荷载；钢桥墩

有限元技术的发展为研究钢结构弹塑性地震反应计算提供了一种有效的方法,但是有限元方法的计算精度取决于采用的材料非线性滞回模型是否合理.目前,循环荷载下钢材的滞回本构模型一般采用基于von Mises屈服准则的等向强化或随动强化模型.研究表明,这两种计算模型的精度不理想.例如,高圣斌等［1-2］采用不同滞回模型计算钢桥墩的滞回性能,并与试验结果进行对比,结果表明,等向强化模型一般倾向于过高预测结构的滞回耗能能力,而随动强化模型相反；Miyoshi等［3-4］分别对钢拱肋和组合梁柱节点在循环荷载下滞回性能进行有限元分析和试验研究,也得到了相似的结论.地震灾害表明,在强震作用下钢桥墩等构件发生塑性损伤是不可避免的［5］,因此钢材滞回模型在塑性域的计算精度对钢桥结构的地震响应计算的影响十分重要.

为了改进钢材滞回模型的计算精度,不少学者对Morz［6］提出的多曲面模型进行修正,例如Dafalias等［7-8］提出用屈服面及边界曲面表示强化系数的双曲面模型,Shen等［9-11］对Dafalias-Popov双曲面模型进行以下改进：考虑了弹性域的缩小及边界面的移动、应力历史对屈服平台的影响以及边界面的大小变化、倾斜等影响,通过修改形状参数的表达式和引入记忆面、虚拟边界面实现控制应力-应变曲线走向的目的.Goto等［2］在双曲面模型的基础上提出三曲面模型,该模型虽然精度有所提高,但存在计算参数多、计算过程复杂的不足.近年来,国内学者开展了钢材的滞回模型研究,例如许红胜等［12-14］在前人理论和试验研究的基础上提出各自的钢材塑性本构模型,为建立高精度的计算模型积累了不少经验.

在已有的钢材滞回模型中,修正双曲面模型是一种兼顾精度和计算量的模型［15-16］.在既有的修正双曲面模型中,当材料由弹性进入塑性（非屈服平台）时,计算得到的塑性模量为无穷大.当加载过程中存在卸载-加载小幅循环的复杂应变历史时,材料塑性模量被高估,将导致不自然的履历响应.为了消除既有修正双曲面模型的上述缺陷,本文对Shen等［9-11］提出的修正双曲面模型进行改进.

1 修正双曲面模型

为了便于说明本文所作的修正内容,对Shen等［9-11］提出的既有修正双曲面模型进行简要的介绍.

1.1 单轴应力状态的双曲面滞回模型

如图1所示为钢材在单轴应力状态下的应力-塑性应变滞回曲线.应力由原点O弹性加载至屈服点A后,经过塑性平台AB后进入塑性强化阶段BC.反方向加载段塑性区域Q1D的塑性模量EP由下式得到：

图1 单轴应力(σ)-塑性应变(εp)滞回曲线Fig.1 Uniaxial cyclic stressσ-plastic strainεp curve

其中,e、f为材料常数.

为了预测应力-应变滞回曲线的走向,修正双曲面模型引入了虚拟边界面和记忆面.如图1所示,曲线DEF段对应的边界面为ZZ′,而记忆面XmX′m为经过历史应力最大点C点,并与C点对应的边界XX′平行的面.记忆面的作用是记录加载点在加载历史上偏离边界面中线OxO′x的最大距离,其中OxO′x为边界XX′和YY′的中心线,记忆面XmX′m和YmY′m在拉、压两侧关于OxO′x对称.

记卸载点D点到记忆面YmY′m的距离为δv；加载曲线DEF对应的虚拟边界面ZvZ′v由边界面ZZ′向加载方向平移δv得到.在预测DE段曲线走向时,塑性模量EP按下式计算：

当加载点达到记忆面（即图1的E点）后,塑性模量EP按式（1）计算,曲线走向为DEF,即曲线不能越过实际的边界ZZ′.

式中：α、a、b、c、ζ为常数；κ0和κ0分别为弹性域和边界面初始半径；为边界面的极限半径,即材料极限强度σu；ρ＝0.5.

修正双曲面模型考虑了应力历史对屈服平台的影响,循环荷载下平台终点的判断准则为

式中：Wp为塑性功,即应力-塑性应变曲线围成的面积；和W分别为单调加载时屈服平台的长度和对应的塑性功；M为常数.另外,修正双曲面模型认为式（1）中的边界斜率随加载历史的塑性功Wp的增大而逐渐减小：

1.2 三维应力状态的双曲面滞回模型

如图2所示,在三维应力空间中,基于von Mises屈服准则的屈服面和边界面为垂直于π平面的圆柱面.图中,αij与βij分别为屈服面和边界面的中心,κ与分别为屈服面和边界面的半径,屈服面和边界面的方程分别为

式中：Sij为偏量应力张量.与单轴应力状态下的计算模型相同,κ与均随等效累积塑性应变曲面的半径ρ而变化,即按式（4）、（5）计算.

三维应力状态下塑性模量EP的计算方法与单轴应力状态相同,但δ及δv须在三维应力空间中定义.首先定义加载点A在边界面（或记忆面）的共乐点为,如图2所示,A与共乐点A在各自曲面上的法向量相同,即

图2 三维应力状态下虚拟边界面和记忆面Fig.2 Virtual bounding surface and memory surface under multiaxial stress state

在三维应力空间中,虚拟边界面和记忆面中心与边界面相同.记忆面的含义与单轴应力状态时相同,半径定义为

若图2中加载至A点时卸载,A点尚未到达记忆面,A与其共乐点基于欧式范数的距离为δm,则下一段加载路径对应的虚拟边界面向外扩张为δv,

通过式（3）得到塑性模量EP后,三维应力状态下的弹塑性应力-应变增量关系可以表示为

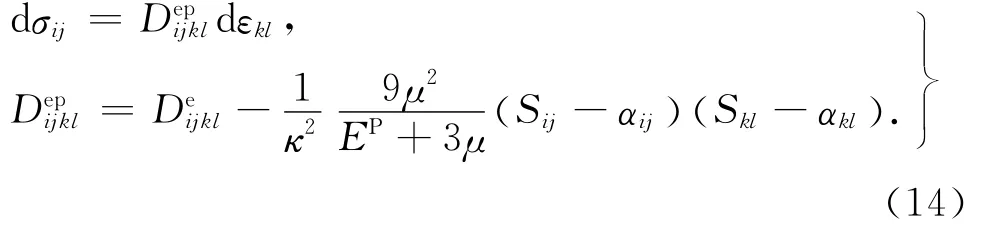
2 考虑复杂应变历史的模型修正

在动力荷载作用下结构经历复杂的卸载-加载变化过程.当应变履历为小幅循环时,在以下两种情形下由式（3）得到的塑性模量EP显著偏高.

1）钢材应力由塑性状态卸载至弹性域内,再重新加载至屈服,即应力-塑性应变曲线沿图3的路径A-B-C-B变化.

2）钢材应力由塑性状态卸载后又小幅反向加载至塑性域,再卸载后沿同向再加载至屈服,即应力-塑性应变曲线沿图4的路径A-B-C-D-E-B变化.

在上述两种情形下,当再次加载进入塑性时,采用既有修正双曲面模型计算得到的EP为无穷大,这与实际情况有明显的差别.本文对上述两种情形下的塑性模量EP计算方法提出如下改进措施.

2.1 单轴应力状态下的修正

2.1.1 第一种情形 图3的应变变化路径为第一种情形.钢材由塑性状态B点卸载至弹性域内的C点后,当再次加载至屈服时,F点、B点分别为反向加载和同向加载对应的屈服点.在既有修正双曲面模型中,无论同向或反向加载,B点或F点处塑性模量EP均为无穷大；但实际情况并非如此,同向加载时B点EP无穷大是不合理的,而反向加载时EP无穷大符合实际.首先须对屈服点的应变变化路径进行判别,以分别确定EP.

图3 第一种情形的单轴应力-塑性应变关系Fig.3 Uniaxial stress-plastic strain relation of case 1

再次加载的方向可以用B点或F点处屈服面的法向量n判别,

式中：α0为弹性域中心的应力.

当B点卸载进入弹性域时,记屈服面的法向量为nin；当再次加载超出弹性域时,记屈服面的法向量为nout.若nout＝nin,即加载点位于图3中的B点,此时式（3）的δin和δv应与AB段一致,计算得到的塑性模量EP应与B点卸载前相同；若nout≠nin,即加载点位于图3中的F点,此时式（3）中的δin和δv应按修正双曲面模型的规则（见图1）更新,按式（3）计算得到的EP为无穷大.如图3所示,修正后的应力-塑性应变曲线的走向由A-B-C-B-E变为A-B-C-B-D,B点处的塑性模量不再为无穷大.

2.1.2 第二种情形 图4的应变变化路径为第2种情形.钢材由塑性状态B点反向加载至C点进入另一侧塑性域,进一步小幅加载至D点后卸载,至E点再次进入塑性.记B点处卸载进入弹性域时的δin和δv为δin,in和δv,in,记CD段塑性应变的变化量为Δεp,应力的变化量为ΔσCD.在E点加载出弹性域时,δin和δv按修正双曲面模型的规则（见图1）更新为δin,out和δv,out,塑性模量EP按式（3）计算；直至自E点起应力的变化量ΔσEF的绝对值超过ΔσCD后（图4的F点）,式（3）的δin和δv按下式计算：

系数r体现CD段进入塑性的程度：

图4 第二种情形的单轴应力-塑性应变关系Fig.4 Uniaxial stress-plastic strain relation of case 2

式中：σy为初屈服应力,E为弹性模量,ξ为常数.式（17）的分母即应变变化的限值,仅当0≤r≤1时认为应变变化幅度较小,须按式（16）对δin和δv进行修正,本文取ξ的值为2.如图4所示,通过式（16）在F点的修正,后段应力-塑性应变曲线FG的走向更加合理.与第一种情形类似,加载方向均可以用加载点在屈服面上的法向量判断.

2.2 三维应力状态下的修正

在三维应力状态下,由弹性域加载至屈服时,加载方向可用加载点处屈服面的法向量nij判断：

式中：Sij和αij分别为应力偏量和弹性域中心.图5（a）对应如图3所示的第一种情形,由A点卸载至弹性域内某点,再加载至B点进入塑性.分别记A、B点处屈服面的法向量为nij,in和nij,out,在三维应力空间中,nij,in和nij,out不一定恰好反向,两者的夹角θ为

与单轴应力状态下相同,当θ＝0时,δin和δv与A点卸载前一致,即δin,in和δv,in；当θ＝π时,δin和δv在C点更新为δin,out和δv,out；若0≤θ≤π,δin和δv按下式计算：

在复杂加卸载路径下,δin和δv随θ的不同而连续变化.

图5（b）对应如图4所示的第2种情形,由A点卸载后反向加载至B点进入塑性,再小幅塑性加载至C点卸载,再加载至D点进入塑性,其间弹性域中心不断移动,半径逐渐缩小.记BC段塑性应变的变化量为,等效应力的变化量为,其中基于von Mises准则的等效应力为

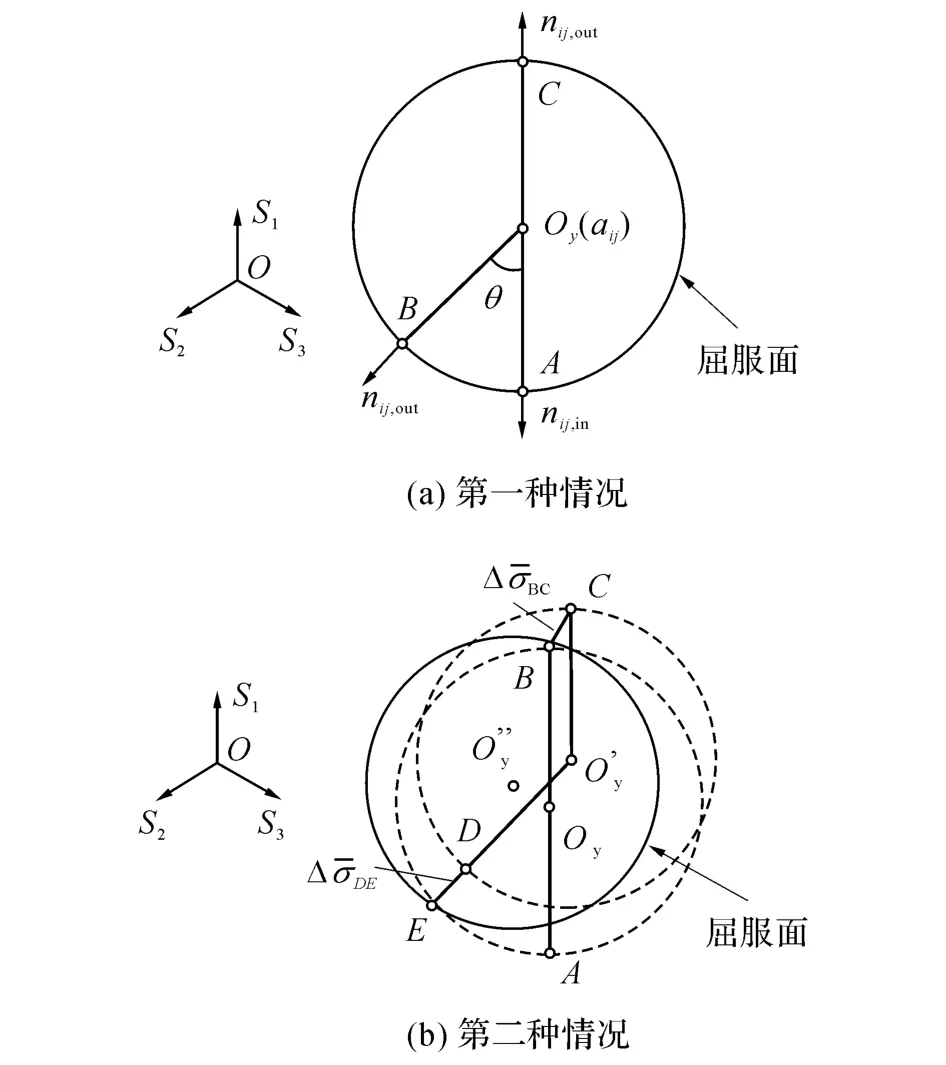
图5 三维应力状态下π平面上的加载路径Fig.5 Loading paths onπplane under multiaxial stress state

与单轴应力状态下相似,在D点进入塑性后,先按式（20）的规则计算δin和δv,塑性模量EP按式（3）计算；直至自D点起等效应力的变化量的绝对值超过,将D点处的δin和δv作为δin,out和δv,out代入式（16）进行计算,但系数r按下式计算：

这种神奇的植物名为“山荷叶”，是山荷叶属植物，属内只有日本山荷叶、南方山荷叶和北美山荷叶，数量稀少，难得一见。

仅当0≤r≤1时须按式（16）修正δin和δv.通过式（16）和（20）,可以在三维应力状态下,对修正双曲面模型进行考虑不同复杂加卸载路径的改进.

3 计算精度以及适用性验证

3.1 精度验证

为了验证改进的修正双曲面模型的准确性和适用性,采用文献［9］中钢材试件SS41-C、SS41-I和SM50-D的循环加载试验结果进行对比验证.所选试件的加载制度均满足本文模型修正的前提,即应变小幅循环的复杂应变历史.其中,试件SS41-C以每个荷载循环0.05%～0.2%的应变增量逐步加载,每步加载后均卸载至弹性域边缘,再继续同向加载；试件SS41-I与SM50-D的加载历史类似,共经过3个荷载循环,最后一个荷载循环的塑性应变增量Δεp较小,满足0≤r≤1的条件.

图6 试件尺寸Fig.6 Dimension of specimens

表1 试件SS41-C、SS41-I和SM50-D的材料参数Tab.1 Model parameters of specimen SS41-C,SS41-I and SM50-D

基于大型通用有限元软件ABAQUS提供的用户子程序接口（user-defined material mechanical behavior,UMAT）Fortran子程序与ABAQUS主程序的数据交流,进而实现改进的修正双曲面模型在结构分析中的应用.在ABAQUS输入文件中使用关键字“*USER MATERIAL”定义用户材料属性.ABAQUS在每个荷载增量步对每个积分点调用UMAT子程序,计算得到材料雅可比矩阵Dep,再进一步形成单元和整体刚度矩阵,用于平衡迭代求解.

如图7所示为计算对比结果.由图7（a）可以看出,试件SS41-C在屈服平台结束后塑性模量EP被既有修正双曲面模型高估,导致强化阶段的应力-应变曲线与试验结果偏离较大,而改进后的模型计算结果与试验吻合较好.另外,从图7（b）、（c）可见,与改进前相比,通过改进后的模型计算得到的试件SS41-I和SM50-D的应力-应变曲线与试验结果更加接近.

由图7可以看出,试件SS41-C与SS41-I相比,前者的应力计算结果的改进效果更加明显,这是由于前者每个荷载循环的塑性应变增量Δεp很小,系数r接近于0,δin和δv经式（16）几乎完全修正为δin,in和δv,in.试件SS41-I系数r超过了0.5,表明原有模型的计算结果与实际较接近.

图7 文献[9]试验与模型计算结果对比Fig.7 Comparison between model analysis and test results in reference［9］

图8 单轴循环荷载下的算例Fig.8 Numerical example under uniaxial cyclic loading

如图8所示为采用3组不同加载方式得到的计算结果,材料参数均采用表1的SM50-D试件.图8（a）、（b）的2个算例均进行一个荷载循环的加载,在A点小幅卸载至B点后重新加载至循环结束.与图7的算例不同,由于图8（a）中A点与边界的距离较大,EP被高估后将对A点之后的应力-应变曲线走向产生较大影响,当应变为－1.5%时,图8（a）中改进后模型计算得到的C点应力为353.4 MPa,而改进前C′点应力为437.9 MPa,相对误差达到23.9%.图8（b）中A点小幅卸载将对下一阶段反向加载的应力-应变曲线走向产生影响,当应变为1.9%时,图8（b）中改进后模型计算得到的C点应力为240.7 MPa,与既有模型的相对误差达到10.4%.

如图8（c）所示为算例3的结果,这是一种较极端的加载方式,即以每个荷载循环塑性应变增量0.05%～0.2%逐步加载,每次加载后均小幅卸载,使应变减小0.02%.由图8（c）可见,在这种循环加载方式下,改进前、后的模型计算结果差异很大,滞回环形状完全不同.当应变为－1.8%时,利用图8（c）中改进后模型计算得到的A点应力为222.6 MPa,而改进前A′点应力为444.9 MPa,相对误差高达100%.对于整个滞回环,塑性功WP在修正前、后的相对误差达到10%以上,说明原有的修正双曲面模型不仅应力计算存在误差,对钢材滞回耗能的预测也不够精确.

3.3 对钢桥墩循环荷载下滞回性能计算结果的影响

由于目前满足本文改进所针对的加载方式的三维应力状态下相关试验的例子比较缺乏,为了检验本文模型改进方法在复杂应力条件下的修正效果,给出独柱钢桥墩在单向和双向小幅加卸载的循环荷载下得到的墩顶水平荷载-位移滞回曲线计算结果.桥墩高3.3 m,截面如图9（a）所示,为带加劲肋的方形截面；加劲肋间距为0.4 m,板厚8 mm.计算模型如图9（b）所示,在墩底使用4节点等参壳单元,其余部分使用弹性梁单元进行模拟.材料参数同表1的试件SM50-D.在钢桥墩顶部施加常轴力N以及图中x、y方向正负循环水平荷载Px和Py,其中N取桥墩屈服轴力的0.15倍.水平荷载的加载方式分别为单向或双向小幅振荡的循环荷载.如图10所示为单向循环荷载加载制度,在x方向采用位移控制加载方法.图中,d为位移,d0为屈服位移,n为循环次数,每次小幅卸载的幅度为0.1d0,位移最终达到5d0.

图9 钢桥墩截面尺寸和计算模型Fig.9 Steel bridge pier section dimension and analysis model

改进前、后模型计算得出的墩顶水平荷载-位移滞回曲线比较结果如图11所示.可以看出,在加载位移持续小幅循环的情形下,改进前的滞回环比改进后饱满、偏大.在前两个荷载循环,改进前、后模型计算得到的荷载-位移滞回曲线几乎一致,随着循环次数和位移峰值的增加,既有修正双曲面模型中钢材塑性模量EP被高估的影响逐渐增大,改进前、后荷载-位移曲线的偏差逐渐增大.这些偏差都是由墩底已进入塑性的单元在小幅循环的荷载作用下累积产生的,墩顶位移越大,墩底进入塑性的单元越多,累积的误差越大.

图10 单向循环荷载加载制度Fig.10 Loading schemes of unidirectional cyclic loading

图11 墩顶荷载-位移滞回曲线Fig.11 Load-displacement hysteretic curve on top of pier

图12 双向循环荷载加载制度Fig.12 Loading schemes of bidirectional cyclic loading

如图12所示为双向循环荷载加载制度,在x、y双向采用位移控制加载方法.图中,dx和dy分别为x、y方向的加载位移,在xy平面上进行2个循环的加载,加载位移在x、y两方向不断增大,并伴随着荷载的小幅振荡.在这种加载方式下,墩顶双向荷载的变化轨迹如图13所示.可以看出,在加载初期模型修正前、后的荷载轨迹一致,但随着荷载小幅振荡次数的增加,既有修正双曲面模型在x、y两方向的墩顶荷载预测结果均趋于偏大,且误差不断增大.这说明改进的修正双曲面模型对钢桥墩在双轴弯曲作用下的滞回性能预测精度有一定程度的改善.

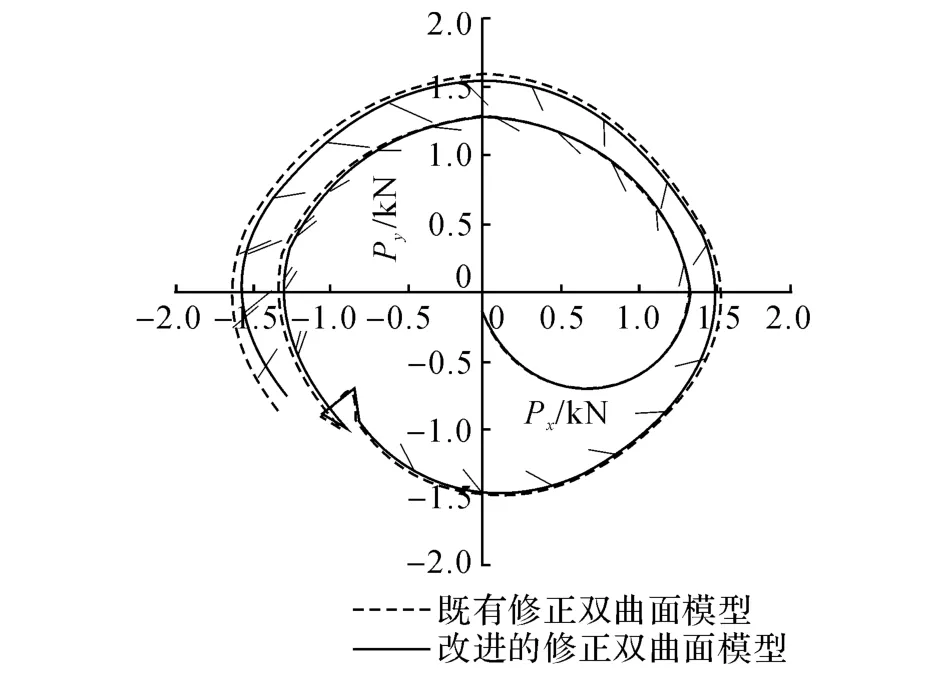
图13 墩顶双向荷载变化轨迹Fig.13 Locus of bidirectional loading on top of pier

4 结 论

（1）通过与文献［9］试验结果的对比,证明修正后的滞回模型有效避免了原有修正双曲面模型对塑性模量EP高估的问题,能够精确地反映钢材在小幅循环的应变历史下的滞回特性,从材料层面验证了本文模型修正的准确性和适用性.

（2）在应变小幅变化的循环荷载作用下,滞回模型修正前、后的应力和耗能计算结果均存在显著差异,本文对修正双曲面模型的改进是必要的.

（3）本文模型修正能够改善钢桥墩单轴和双轴弯曲作用下的滞回性能计算精度.

［1］高圣斌,葛汉彬.交替荷载作用下钢材本构模型的使用范围［J］.中国公路学报,2008,21（6）：69- 75.

GAO Sheng-bin,GE Han-bin.Applicable range of steel constitutive models under cyclic load［J］.China Journal of Highway and Transport,2008,21（6）：69- 75.

［2］GOTO Y,WANG Q,OBATA M.FEM analysis for hysteretic behavior of thin-walled column［J］.Journal of Structure Engineering,ASCE,1998,124（11）：1290- 1301.

［3］MIYOSHI T,SAKIMOTO T,TSURUTA E,et al. Effect of hardening rules of steel on the analysis of cyclic behavior of steel structures［J］.Journal of Structural Engineering,JSCE,2003,49A：403- 413.

［4］SHI G,WANG M,BAI Y,et al.Experimental and modeling study of high-strength structural steel under cyclic loading［J］.Engineering Structures,2012,37：1- 13.

［5］日本土木学会.阪神淡路大震災における鋼構造物の震災の突態と分析［M］.東京：丸善,1999.

［6］MORZ Z.An attempt to describe the behavior of metal under cyclic loads using a more general work hardening model［J］.Acta Mechanica,1969,7（2／3）：199- 212.

［7］DALAFALIS Y F,POPOV E P.A model of nonlinearly hardening material for complex loading［J］.Acta Mechanica,1975,21（3）：173- 192.

［8］DALAFALIS Y F,POPOV E P.Plastic interval variables formalism of cyclic plasticity［J］.Journal of Applied Mechanics,ASME,1976,43（4）：645- 651.

［9］SHEN C.Development of a cyclic two-surface model for structural steels with yield plateau［D］.Nagoya：Nagoya University,1993.

［10］SHEN C,MIZUNO E,USAMI T.A Generalized two-surface model for structural steels under cyclic loading［J］.Journal of Structural Mechanics and Earthquake Engineering,JSCE,1993,471（I-2）：23- 33.

［11］SHEN C,MAMAGHANI I,MIZUNO E,et al.Cyclic behavior of structural steel,II：theory［J］.Journal of Engineering Mechanics,ASCE,1995,121（11）：1165- 1172.

［12］许红胜,熊辉.钢结构塑性分析的新模型［J］.工程力学,2004,21（5）：161- 165.

XU Hong-sheng,XIONG Hui.A new model for plastic analysis of steel structures［J］.Engineering Mechanics,2004,21（5）：161- 165.

［13］石永久,王萌,王元清.结构钢材循环荷载下的本构模型研究［J］.工程力学,2012,29（9）：92- 98.

SHI Yong-jiu,WANG Meng,WANG Yuan-qing.Study on constitutive model of structural steel under cyclic loading［J］.Engineering Mechanics,2012, 29（9）：92- 98.

［14］王萌,石永久,王元清,等.循环荷载下钢材本构模型的应用研究［J］.工程力学,2013,30（7）：212- 218.

WANG Meng,SHI Yong-jiu,WANG Yuan-qing,et al.Applications study on cyclic constitutive model of steel［J］.Engineering Mechanics,2013,30（7）：212- 218.

［15］USAMI T,GAO S,GE H.Elastoplastic analysis of steel members and frames subjected to cyclic loading［J］.Engineering Structures,2000,22（2）：135- 145.

［16］GE H,GAO S,USAMI T.Stiffened steel box columns.Part 1：cyclic behavior［J］.Earthquake Engineering and Structural Dynamics,2009,29（11）：1691- 1706.

Modified two-surface steel hysteretic model considering complex strain history

WANG Tong1,XIE Xu1,TANG Zhan-zhan1,SHEN Chi2
（1.College of Civil Engineering and Architecture,Zhejiang University,Hangzhou 310058,China；2.International Project Group,Chodai Co.,Ltd.,Ibaraki 305-0812,Japan）

The shortcomings of modified two-surface hysteretic model,which is a steel elasto-plastic hysteretic constitutive model that consider both analysis accuracy and efficiency,were taken as research object.The problem that under complex strain history,sometimes the stress results obtained by the model are irrational since the plastic modulus at the critical point between elastic and plastic stage tends to infinite,was to be avoid.The existing modified two-surface model was remodified by improving its criterion of stress-strain path.The improving method of the analysis model under uniaxial and multiaxial stress state was given.The comparison results with analysis results and uniaxial tensile and compression tests, and a series of example analysis show that the improved model can precisely predict the hysteretic property of steel under complex strain history.The accuracy and applicability of the improving method were validated at material and structural member level.Results show that improvement of existing modified two-surface model can effectively raise the computational precision under complex strain history of the model.

modified two-surface hysteretic model；steel；cyclic loading；steel bridge pier

10.3785／j.issn.1008-973X.2015.07.015

U 443

A

1008- 973X（2015）07- 1305- 08

2014- 11- 20. 浙江大学学报(工学版)网址：www.journals.zju.edu.cn／eng

国家自然科学基金资助项目（51378460）.

王彤（1988－）,男,博士生,从事桥梁和钢结构抗震研究.ORCID：0000-0002-3004-4894.E-mail：wangtong＠zju.edu.cn

谢旭,男,教授.ORCID：0000-0002-4247-0487.E-mail：xiexu＠zju.edu.cn