基于Petri网的飞机总装配生产线建模及优化方法
2015-10-24温李庆李江雄柯映林张世炯
王 青,温李庆,2,李江雄,柯映林,李 涛,张世炯
(1.浙江大学机械工程学院,浙江杭州310027;2.中国人民解放军94982部队,安徽安庆246005;3.中航工业成都飞机工业(集团)有限责任公司总装厂,四川成都610092)
基于Petri网的飞机总装配生产线建模及优化方法
王 青1,温李庆1,2,李江雄1,柯映林1,李 涛3,张世炯3
(1.浙江大学机械工程学院,浙江杭州310027;2.中国人民解放军94982部队,安徽安庆246005;3.中航工业成都飞机工业(集团)有限责任公司总装厂,四川成都610092)
针对飞机总装配生产线最优化调度问题,建立能够描述飞机脉动式总装配生产线工艺流程间复杂关系的赋时库所Petri网(TPPN)仿真模型.在飞机总装配工序的前后继关系和有限的车间资源约束下,以工期最短、工作组最少和工作组的总效率最高为优化目标,提出生产线调度问题的多目标优化模型.采用逐层法进行最优化求解,根据关键路径推算公式确定生产线的最短工期和最少工作组数,采用贪心-匈牙利两级递阶算法获得生产线的最佳人工分配方案和最优作业排序.通过应用实例,验证了优化方法的准确性和有效性.
Petri网;飞机总装配;生产线;最优化调度
飞机装配是根据飞机设计要求将飞机零件、组件、部件进行定位、连接,形成高层次装配体或整机的复杂过程.由于飞机结构形式及系统组成复杂,装配工作量巨大,约占整个飞机制造劳动量的40%~50%[1].波音公司上世纪90年代在B717总装配中基于精益思想建立连续移动式总装配生产线,后续推广到B737、B777等飞机;洛克希德马丁公司在F-22、F-35战斗机总装配中建立了移动生产线;空客公司主要以站位移动式(简称脉动式)总装配生产线为主[2].
飞机总装配生产线技术在我国飞机制造企业中的应用尚处于起步阶段,在质量控制、作业安排、人员管理、物流配送等方面都不能满足新型飞机装配的要求.如何实现脉动式或连续移动式飞机总装配生产线的合理规划和工艺调度,是目前我国飞机制造企业迫切需要解决的问题.
飞机装配生产线仿真建模及最优化调度是实现生产线合理规划的基础.Ramchandani[3]在基本Petri网的基础上率先提出赋时Petri网(timed Petri Net,TPN)理论.Rivera等[4]探讨了离散制造系统简化Petri网模型的建立方法.针对柔性制造系统(flexible manufacturing system,FMS)调度问题,Li等[5]提出基于TPN的同步激发策略,使用该策略能够快速得到FMS最优调度解.Zhang等[6]应用TPN模型解决了FMS动态调度难题.在汽车制造领域,Young等[7]采用基于TPN模型的两级分层调度方法,获得了汽车生产线的最优调度方案,适用于大规模、混线生产的流水线作业模式.在飞机装配领域,Liu等[8-9]提出面向对象分层次随机Petri网(HOSPN)的建模方法,应用该方法建立了客机装配的工艺流程模型.该方法的建模过程复杂,主要用于生产线布局的改善,未涉及资源调度的优化问题.
本文根据某型飞机脉动式总装配生产线的建设要求,针对生产线最优化调度问题,建立该型飞机脉动式总装配生产线的赋时库所Petri网(timed place Petri net,TPPN)仿真模型.通过综合考虑并合理简化生产线的约束条件及优化目标,提出生产线调度问题的多目标优化模型.采用逐层求解的方法得到生产线的最优化调度结果,将求解结果应用于飞机生产线调度.
1 基于TPPN的飞机生产线仿真建模
1.1 飞机脉动式总装配生产线简介
某型飞机脉动式总装配生产线总体布局如图1所示。依据生产均衡性原则,将生产线划分为4个站位,分别为:大部件对接站位、导管电缆安装站位、系统检测站位、飞机交付站位。飞机大部件从大部件对接站位进入生产线,最终在飞机交付站位完成所有总装配工作。在连续生产情况下,生产线的生产周期等于各站位工作节拍的最大值.生产线站位使用工艺流程图将站位工序及流程以图表的形式进行说明,作为各站位调度工作的参考.大部件对接站位工艺的流程图如图2所示.
利用工艺流程图可以简洁地说明生产线需要完成的工序以及完成这些工序的大致流程,但缺乏对生产流程中工序间的前后继约束关系及工序的并发、同步、异步特征的描述能力.
1.2 生产线TPPN模型的构建方法
飞机脉动式总装配生产线是典型的离散事件系统.采用赋时库所Petri网,即TPPN理论,可以建立考虑时间因素的离散事件系统的图形化仿真模型[10].仿真模型对单项工序的描述如图3所示.图中,变迁ti1表示工序i的开工,ti2表示工序i的完工.对库所pi赋予时间权值di,表示从ti1发生(pi获得标识)开始,至少要经过di个单位时间ti2才可以发生.

图2 大部件对接站位工艺流程Fig.2 Process of docking station

图3 单项工序的TPPN模型Fig.3 TPPN model for individual procedure
针对飞机脉动式总装配生产线,可以通过如下步骤建立TPPN模型.
1)若工序i是工序j的前提工序,则在ti2和tj1之间加入库所pij,如图4所示,并对pij赋予时间权值dij=0.
2)对于那些无前提工序的工序,将代表它们各自开工的变迁合并成为一个,并引入初始库所po,对po赋予时间权值do=0.
3)对于那些无后续工序的工序,把代表它们各自完工的变迁合并成一个,引入结束库所pe,对pe赋予时间权de=0.
4)设置初始标识M0,使得M0(po)=1, M0(p)=0( p ≠po).
5)在不改变工序之间衔接关系的前提下,消去某些零权库所(po、pe不能消去),把它们所连接的前一工序的完工变迁和后一工序的开工变迁合并成一个.最大限度消去零权库所后,生产线每个工序由一个库所来表示.对于化简过程中为了不改变工序间的衔接关系而不得不保留的那些零权库所,称为虚拟工序库所.

图4 衔接工序TPPN模型Fig.4 TPPN model for linking procedure
1.3 生产线TPPN模型的运行规则
飞机脉动式总装配生产线中的某道工序必须在所有前驱工序均已完工的情况下才能进入开工状态,生产线的运行过程是生产线工序在等待开工、加工中、完工等状态间不断转变的过程.为了对生产线的运行进行仿真分析,采用生产线TPPN模型的运行规则,定义如下.
定义1 TPPN模型的使能规则[11]如下:
变迁ti∈T在标识M下使能(数学表达式为:M[ti>),当且仅当
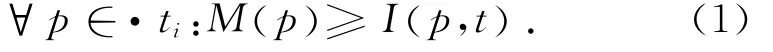
式中:·t表示t的所有输入库所.
定义2 在标志M下使能的变迁t的激发将产生新标识M′[11]:
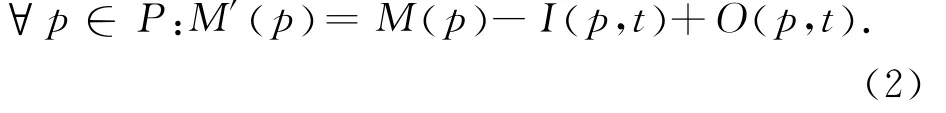
1.4 飞机脉动式总装配生产线TPPN模型的建立
在建立飞机脉动式总装配生产线的TPPN仿真模型时,由于生产线过于复杂且各站位的建模过程类似,本文仅详细介绍大部件对接站位的建模过程.大部件对接站位工艺流程如图2所示,其中0140、0150号工序的并行工序多,生产安排中存在工艺路线约束复杂、可并行作业工序多、资源调度困难等问题.0140、0150号工序的前后工序均为简单串行工序,不存在调度难题,因此建立大部件对接站位0140、0150号工序及并行工序的TPPN仿真模型.模型中,工序编号、工序内容、工期及前驱工序如表1所示,根据表1建立的TPPN仿真模型如图5所示.

表1 大部件对接站位TPPN模型工序信息Tab.1 Information of TPPN model for docking station

图5 大部件对接站位重点工序TPPN仿真模型Fig.5 TPPN model of key procedure in docking station
2 生产线调度问题的多目标优化模型
2.1 生产线调度问题描述
飞机的总装配从飞机大部件进入装配线开始,需要在计划期内完成飞机的部件装配及功能试验等所有工序,这些工序分属于不同的站位.生产线调度问题主要集中在站位内工序如何安排和资源如何分配,站位间的调度更依赖经验丰富的工艺员进行全局规划,因此将生产线调度问题简化为生产线站位内调度问题.生产线站位内调度问题描述如下:m道工序需要指派给n个工作组完成;工序间存在前后继关系约束;每道工序可由多个但仅能选其中一个工作组完成;不同的工作组完成同一道工序的效率不同;同一个工作组在某一时段只能从事一道工序;工序一旦开工便不能中断.
调度目标为:工期最短;工作组最少;工作组的总效率最高,且逐级递进地满足上述3个目标.
2.2 生产线调度问题的多目标优化模型
由问题描述可知,生产线最优化调度问题是完全分层多目标优化问题,数学模型如下:

式中:f1(X) 为第1优先层,f2(X) 为第2优先层,-f3(X) 为第3优先层.
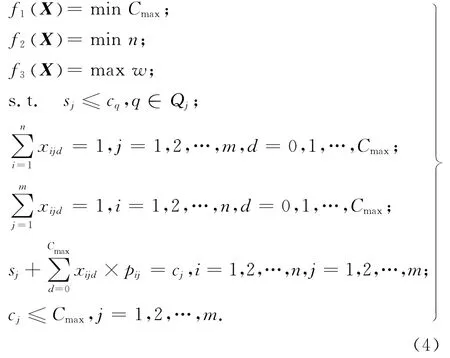
式中:Cmax为工期;n为工作组数,其中i=1,2,…,n为工作组编号;m为工序数,j=1,2,…,m为工序编号;w为工作组总效率;sj为工序j开工时间;cj为工序j收工时间;Qj为工序j的紧前工序集;pij为工作组i完成工序j所需时间;d=0,1,…,Cmax为离散时间节点,定义决策变量:

式(4)中的约束条件依次如下.工序前后继关系约束;某时间节点一道工序只能由一个工作组开工;某时间节点一个工作组只能开工一道工序;工序加工过程连续性约束;工序的完工时间不能超过总工期.
3 多目标优化模型的解法
针对式(4)的多目标优化模型,根据模型的优先层次逐层求解,上一优先层的最优解即为下一优先层的可行域.首先,求解第1优先层,确定生产线的最短工期;然后,基于最短工期的计算结果求解第2优先层,确定生产线需要的最少工作组数;最后,采用贪心-匈牙利两级递阶算法求解第3优先层.贪心算法通过合理地选取决策点,将最优化调度问题转换为分阶段指派子问题,指派子问题利用匈牙利算法求出局部最优解,最终组合子问题的局部最优解得到工作组总效率最高的最优化调度结果.
3.1 最短工期的确定
飞机脉动式总装配生产线的TPPN模型描述了实际生产线中工序的前后继关系及各工序耗时.根据该模型,采用关键路径推算公式可以计算出各工序的最早可开工时间、完成整个生产线流程的最短工期、保证最短工期的各工序pi最晚必须开工时间.推算公式如下.
定理1 E(pi)表示工序pi的最早可开工时间,TE表示完成整个生产线流程的最短工期, L(pi)表示为保证生产线在最短工期TE内完工、工序pi最晚必须的开工时间[11].

式中:·p和p·分别表示库所p的所有输入与输出变迁,pe为Petri网中的结束工序.
3.2 最少工作组的确定
基于最短工期的计算结果,利用定理2可以得到生产线的关键路径;利用定理3可以得到最少并行作业工作组数.
定理2 生产线的关键路径集{pi}为满足下列条件的所有工序[11]:
1)位于po指向pe的一条有向路上;
2)该有向路上所有的工序pi均满足E(pi)=L(pi);
3)非开始、结束及虚拟工序.
定理3 设∑为某装配生产线的TPPN模型.P(ti,tj)是∑中的一个并发段,MTL(∑ )是∑的一条关键路径,P(ti,tj)表示并发段P(ti,tj)中全部库所的集合,则可得下式[11].
1)并发段P(ti,tj)的最短执行时间为
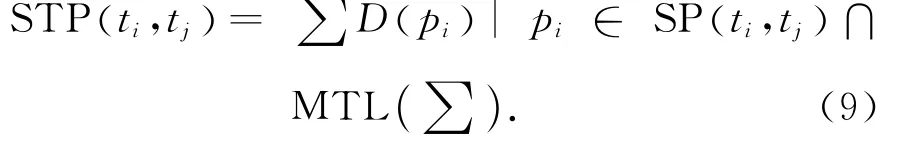
2)为了保证执行时间最短,该并发段所需的工作组的最小数目为

3.3 最优化调度问题的分解和转换
求解最优化问题的算法通常需要经过一系列的步骤,在每个步骤都面临多种选择.贪心算法在问题的每一步都作出当前最佳的选择,即得到问题的局部最优解,并组合局部最优解得到问题的全局最优解[12].
深入分析飞机脉动式总装配生产线可知,调度过程存在以下特点:随着时间的推移,生产线不断有工序完工,从而不断有工作组进入空闲等待派工、可开工工序进入等待指派状态.最优化调度是在时间推移中做出最优指派的决策.贪心算法适用于飞机脉动式总装配生产线最优化调度问题,贪心-匈牙利两级递阶算法描述如下.
算法1 贪心-匈牙利两级递阶算法
1)初始化.初始化时间t=0,输入矩阵I、输出矩阵O,工序时延集D,已开工工序剩下时延集d,已完工工序标识集W,新完工工序标识集w,已开工工序标识集M,待开工工序标识集N,激发的变迁集δ,表示指派结果优劣的全局误工系数cost=0.
2)时间推移.由已开工工序集剩下时延d(pi)、待开工工序集最晚必须开工时间L(pj)和时间t得到变迁激发时延α=min{{d(pi)}∪{L(pj)-t}},时间推移结果为t=t+α.由时延公式可知,时间推移的结果为产生新完工工序或产生急需派工工序.
3)判断新完工工序标识集w是否为空.若是,则表示未产生新完工工序,转4)进一步判断;若否,则表示产生新完工工序,转5).
4)判断待开工工序标识集N是否为空.若是,则无等待派工工序,转5);若否,则表示有紧急工序等待指派,此为分阶段指派决策点,转10)进行派工.
5)调用激发函数.
6)判断激发函数返回的激发变迁集δ末位否为1.若是,则表示仿真到达结束工序,调度结束,输出结果;若否,则转7).
7)判断δ是否为空.若是,则无变迁激发,转9);若否,变迁激发将产生新的待开工工序,更新已完工工序标识集W、待开工工序标识集N,转8).
8)判断待开工工序标识集N中是否有虚拟工序.虚拟工序D(di)=0,不参与指派.若是,则令W(di)=1,N(di)=1,转5);若否,则转9).
9)判断已开工工序标识集M是否为空.若是,则工作组均处于空闲等待派工状态,此为分阶段指派决策点,转10)进行派工;若否,则转2).
10)调用指派函数.指派函数面向待开工工序标识集N对空闲工作组进行派工,并将分阶段派工的局部误工系数以迭加的形式计入全局误工系数cost.求解指派问题的匈牙利算法在3.4节中阐述.
算法1的流程如图6所示.

图6 贪心算法流程图Fig.6 Flow chart of greedy algorithm
3.4 指派问题的求解
贪心算法将最优化调度问题转换为分阶段指派子问题,在分阶段指派决策点遇到如下子问题的优化:指派n个工作组完成m道工序,已知工作组i完成工序j的效率为cij,各工作组完成一道不同的工序,如何优化安排工作组从事的工序才能使得整体工作效率最高?该问题为指派问题,也称为最佳匹配问题.匈牙利算法是解决该类问题的有效算法,该算法的核心是寻找增广路径,用增广路径求取二分图的最佳匹配[13].
匈牙利算法解决的是效率矩阵为方阵、即工作组数和工序数相等的指派问题,对于效率矩阵不是方阵的指派问题模型,存在以下几种情况及对应的解决办法.
1)工作组多工序少.可以添加一些虚拟的工序,各工作组完成这些工序的效率可以取为0.
2)工作组少工序多.可以添加一些虚拟的工作组,他们完成各工序的效率可以取为0.
通过上述方法添加虚拟工作组或虚拟工序,将效率矩阵为非方阵的指派问题转化成效率矩阵为方阵的指派问题,且转换后不影响指派结果.
匈牙利算法只能求解最小化优化问题,因此引入误工系数,将最大效率对应最小误工系数,即由效率矩阵C得到误工系数矩阵B,将最大化效率问题转换为最小化误工系数问题.转换方法为在效率矩阵C中找出最大数m=max{cij},然后进行矩阵变换B=m I-C.通过转换,将原最大化效率指派问题模型转换为同解的最小化误工系数指派问题模型:

再利用匈牙利算法求解.
4 应用实例
以某型飞机总装配生产线为例,由于站位工艺的分组及调度主要依赖个人经验,易于出现人员管理混乱、装配作业交叉、站位计划拖延等问题,具体而言:一、二站位经常出现工作节拍超过计划节拍,飞机交付拖延;三、四站位可以按计划节拍生产,但工作组空闲等待情况严重,资源利用率不高.
本文生产线TPPN仿真模型的运行规则及多目标优化模型的解法采用Matlab编程实现,应用本文算法已较好地解决该生产线存在的问题.限于篇幅,本文仅详述第一站位(大部件对接站位)的求解过程,其他站位的求解过程类似,仅列出求解结果.
4.1 第一站位求解结果与分析
由表1、图5得到第一站位调度问题的初始条件,运行最短工期函数,得到如表2所示的结果,取最少工作组数完成装配任务.

表2 第一站位最短工期函数运行结果Tab.2 Results of shortest duration function for first station
所选装配任务除去开始、结束及虚拟工序,总计有12道工序指派给3个工作组.12道工序按工作内容大致区分为如表3所示的3大类.从专业化生产的角度出发,规定每个工作组优先指派某一类工序,以效率来表明工作组对该类工序的熟悉程度.效率权重值为1,数值越大,熟悉度越高,如表4所示.

表3 第一站位工序分类Tab.3 Classification of procedures in first station

表4 第一站位工作组效率Tab.4 Efficiency of working groups in first station
根据表4、式(11),可得最小化指派问题的误工系数矩阵.
根据以上初始条件,运用本文算法得到最优化调度结果,优化调度前、后的甘特图如图7所示.将调度结果用于指导第一站位调度,得到应用最优化调度方法前、后该站位各参数的对比,如表5所示.

图7 第一站位复杂工序优化前、后对比图Fig.7 Comparison of Gantt chart for complex process in first station before and after using optimal method

表5 第一站位应用最优化方法前、后各参数对比Tab.5 Comparison of various parameters of first station before and after using optimal method
4.2 其他站位求解结果
分别建立导管电缆安装站位、系统检测站位、飞机交付站位重点工序的TPPN仿真模型、多目标优化模型并调用多目标优化模型的求解函数,得到各站位重点工序的最优化调度结果.将调度结果用于指导各站位的调度,得到应用最优化调度方法前、后各站位相关参数对比如表6所示.
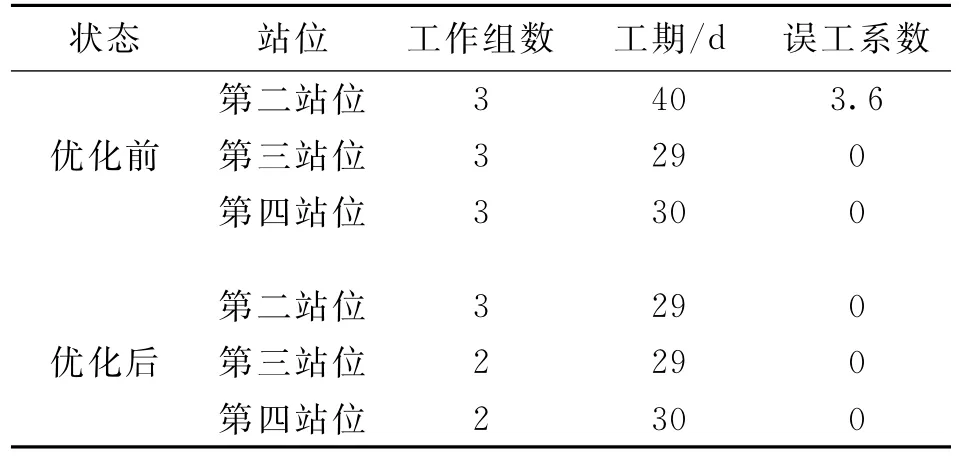
表6 各站位应用最优化调度方法前、后相关参数对比Tab.6 Comparison of various parameters of other stations before and after using optimal method
由表5、6可知,通过应用本文提出的最优化调度方法,使得某型飞机生产线的生产周期由41 d减少至30 d,工作组数由12组减少至10组,且工作组均被指派从事其最擅长的工作,生产效率得到显著提高.
5 结 论
(1)本文所提出的生产线工艺流程TPPN仿真模型体现了飞机生产线离散状态、事件驱动的特性,描述了生产线工序间的前后继约束关系及工序的并发、同步、异步特征.
(2)飞机生产线调度问题的多目标优化模型是对复杂生产线调度问题的合理简化.通过逐层求解多目标优化模型,能够迅速地得到满足需求的最优解.
(3)通过应用上述建模及优化方法,使飞机生产线的生产周期缩短,工作组数量减少且均被指派其最擅长的工作,生产效率得到显著提高.
[1]王云渤,张关康,冯宗律,等.飞机装配工艺学(修订本)[M].北京:国防工业出版社,1990.
[2]范玉青,梅中义,陶剑,等.大型飞机数字化制造工程[M].北京:航空工业出版社,2011.
[3]RAMCHANDANI C.Analysis of asynchronous concurrent systems by timed Petri nets[D].Cambridge:MIT,1974.
[4]RIVERA R I,RAMIREZ T A,LOPEZ M E.Building reduced petri net models of discrete manufacturing systems[J].Manufacturing and Computer Modeling,2005, 41(8):923- 937.
[5]LI Cheng,WU Wei-min,RONG Gang.Heuristic search and concurrency strategy based on Petri net for FMS scheduling[J].Networking,Sensing and Control, 2014,64(5):80- 85.
[6]ZHANG Wei-jun,THEODOR F,YANG Hua-shu.Dy-namic scheduling in flexible assembly system based on timed Petri nets model[J].Robotics and Computer-Integrated Manufacturing.2005,21(6):550- 558.
[7]YOUNG W K,INABA A,SUZUKI T,et al.Hierarchical scheduling for large-scale production system based on continuous and timed Petri net model[C]//Proceedings of the 41st SICE Annual Conference.Piscataway:IEEE,2002:268- 271.
[8]LIU Xia,YE Wen-hua,WEI Bi-sheng,et al.Research on multi-level modeling method for aircraft assembly line[J].Advanced Materials Research,2012,490- 495:538- 542.
[9]LU Hu,LIU Xia,PANG Wei,et al.Modeling and simulation of aircraft assembly line based on quest[J].Advanced Materials Research,2012,569(2):666- 669.
[10]GRADISAR D,MUSIC G.Production-process modeling based on production-management data:a Petri-net approach[J].International Journal of Computer Integrated Manufacturing,2007,20(8):794- 810.
[11]吴哲晖.Petri网导论[M].北京:机械工业出版社, 2006.
[12]CORMEN T H,LEISERSON C E,RIVEST R L,et al.Introduction to algorithms[M].Cambridge:MIT, 2013.
[13]王树禾.图论[M].北京:科学出版社,2004.
Modeling and optimization for aircraft final assembly line based on Petri net
WANG Qing1,WEN Li-qing1,2,LI Jiang-xiong1,KE Ying-lin1,LI Tao3, ZHANG Shi-jiong3
(1.School of Mechanical Engineering,Zhejiang University,Hangzhou 310027,China;2.94982 Troops,PLA,An'qing 246005,China;3.Assembly Plant,AVIC Chengdu Aircraft Corporation,Chengdu 610092,China)
A timed place Petri Net(TPPN)model for pulse final assembly line was constructed to describe the complex logical relationship of the assembly process in order to optimize the scheduling of aircraft final assembly line.A multi-objective optimization model was proposed under the constraints of limited workshop resources and the successive relationship in aircraft assembly process in order to achieve the following goals:the shortest duration,the minimum working groups,and the highest overall efficiency of working groups.A hierarchical solving strategy was adopted to obtain the optimal solution.The formula of critical path method(CPM)was used to figure out the shortest duration and the minimum working groups.Then the greedy Hungary algorithm(GHA)was applied to obtain the reasonable arrangement of human resources and optimal job sorting.An example of aircraft final assembly line was provided to verify the accuracy and effectiveness of the simulation and optimization method.
Petri net;aircraft final assembly;production line;optimal scheduling
10.3785/j.issn.1008-973X.2015.07.004
V 260
A
1008- 973X(2015)07- 1224- 08
2014- 10- 17. 浙江大学学报(工学版)网址:www.journals.zju.edu.cn/eng
国家自然科学基金资助项目(51375442).
王青(1979-),男,副教授,从事飞机数字化装配技术及系统集成的研究.ORCID:0000-0003-4318-7867.
E-mail:wqing@zju.edu.cn
