时延差双曲面定位方法在鱼雷入水点测量中的应用

李韦华，　薛　飞，　马锦垠

（中国人民解放军91439部队， 辽宁 大连， 116041）

时延差双曲面定位方法在鱼雷入水点测量中的应用

李韦华，薛飞，马锦垠

（中国人民解放军91439部队， 辽宁 大连， 116041）

针对鱼雷入水点实时测量无法获取的问题， 给出了一种基于多个阵元联合定位的时延差双曲面定位方法， 该方法可以测量目标大地坐标并达到10 m的定位精度（标准误差）而无需矢量的方位数据， 同时讨论了浮标阵的测时误差对定位精度的影响， 结果表明， 浮标阵内测量误差最大不超过4 m。海上试验验证了该方法的有效性。

鱼雷； 时延差； 双曲面； 浮标阵

0　引言

火箭助飞鱼雷入水点定位是后续测量鱼雷航行轨迹的重要环节。而火箭助飞鱼雷入水信号弱， 容易被环境噪声所掩盖， 因此常常通过布设多个阵元来实现对目标的精确定位［1］。

文中基于多个阵元的联合定位提出了一种时延差双曲面交汇被动定位技术， 其优点是可以测量目标大地坐标并达到10 m的定位精度（标准误差）而无需矢量方位数据。该方法一般作为鱼雷入水点位置测量的补充方式， 以提高执行试验任务的可靠性。多个浮标接收到的原始声信号通过通信链上传至信号处理平台进行集中式处理， 原始波形的回传给无线电通信链带来很大的负担， 因此往往不作为实时信号处理方案， 而是在实验室平台上对接收信号进行事后处理［2］。

1　时延差双曲面定位方法的基本原理

假定在一个局部测量区域布设4个浮标， 以海平面为xoy平面， 建立右手直角坐标系， 如图1所示。设目标位置为（x， y， z）， 4个阵元的坐标已知， （xi，yi，zi），i=1，2，3，4， 由浮标中i， j阵元测得的时延差τij可得定位方程

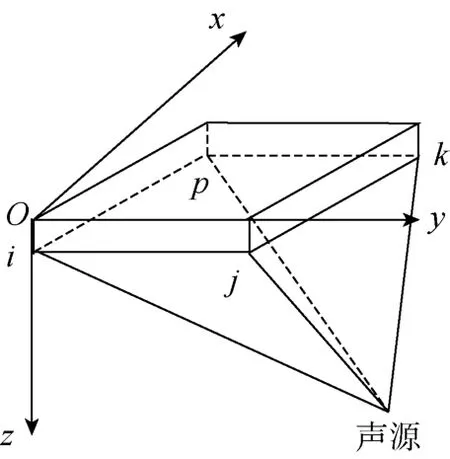
图1　浮标阵与目标方位示意图Fig.1　Schematic of buoy array and target azimuth

式中： τij=τi-τj， τi为从目标到阵元i的传播时延； c为声速。目标位置一定在由式（1）确定的双曲面上， 将式（1）移项平方得

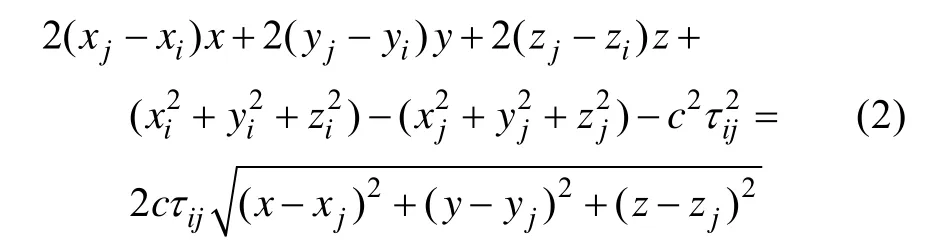
令

测量系统中有4个阵元， 两两间有多组时延差， 任取其中至少的3个相互独立时延差建立方程组可以解出目标的水平位置［3-4］。

i号浮标距离坐标系原点距离

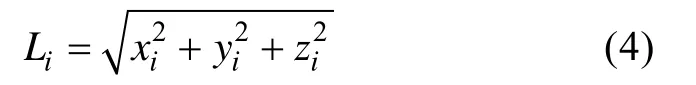
j号浮标距离坐标系原点距离

目标到j号浮标的距离

令

那么， 式（2）可简化为

由于在布设浮标时， 采用的浮标完全一致，因此深度方向上Δzji=0， 同样， 对于j，k号浮标有

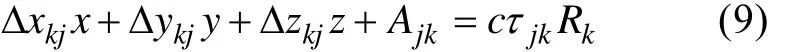
对于k，p号浮标有

由上面3式可得

通过求解式（11）的一元二次方程得声源的坐标位置

2　海上试验验证

为了检验上述方法的实用性， 利用时延差双曲面定位方法实现了对某次试验中鱼雷入水位置、鱼雷出水位置的精确定位。试验前， 按照预先设定的浮标位置进行布放， 浮标阵1， 2， 3， 4的位置坐标为（84.13， 1 098）， （-199.52， 300.53），（-43.8， -1 360）， （1 012.4， -97.88）。4个浮标的位置成菱形， 布放时以鱼雷的理论入水点为中心点进行布放。其中， 4个浮标接收到鱼雷入水点信号的时间分别为427.346 7 s， 426.781 0 s， 426.857 4 s，427.287 1 s。将浮标接收到的4个时间依次相减，可获得3个时延差。注意， 此处采用的时延差不能形成闭循环。将上面4个浮标位置和3个时延差带入式（12）可得鱼雷的入水点。4个浮标所接收到鱼雷入水点信号的时间分别为631.148 0 s，630.689 7 s， 630.803 6 s， 630.711 1 s。处理方法同上。浮标位置与鱼雷入水、出水位置等见图2。

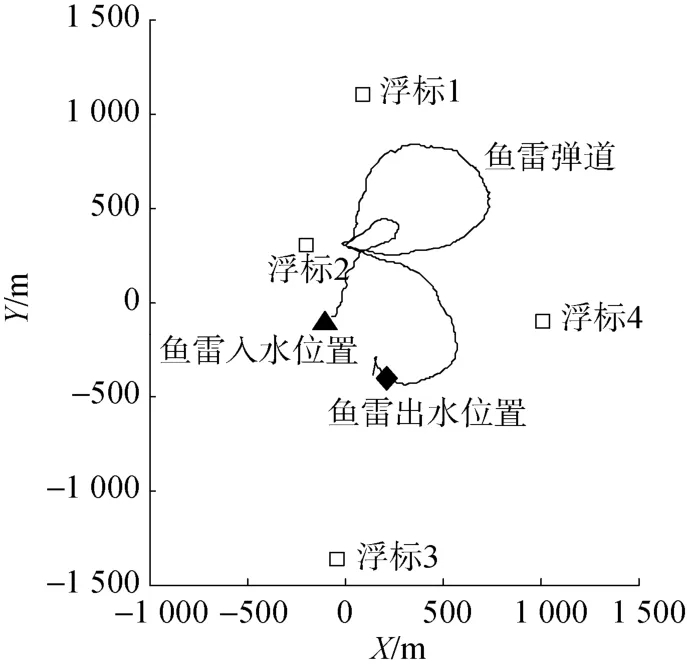
图2　海上实测数据定位Fig. 2　Localization by data from sea trial

3　测时误差对测量精度的影响

在求解声源目标的水平坐标（x， y）时， 测量误差一般由浮标位置的测量误差、时延值的测量误差决定， 一般认为浮标位置的测量误差受海流的影响， 是一个固定误差， 而时延值的误差则是由人工判读信号时引入， 这里采用测时误差0.5 ms， 对测量精度的影响进行仿真［5］。

文中共设置4个浮标， 位置分别为（-1 500，0）， （1 500， 0）， （-1 500， 1 500）， （1 500， 1 500）， 声源位置在1 500 m×1 500 m范围内变化， 分别求出加入误差后的声源位置， 再求出与实际坐标的差值。如图3所示， 引入测时误差0.5 ms时， 声源的测量误差最大不会超过4 m， 且声源的位置越靠近4个浮标的中心位置， 测量误差越小， 而靠近任意2个浮标的连线时误差就会变大， 这与实际情况相符。

4　结论

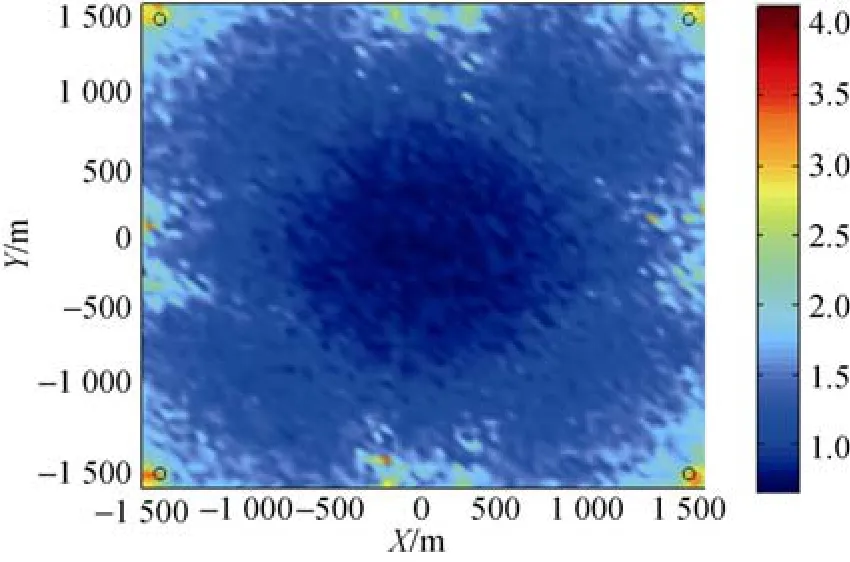
图3　测时误差0.5 ms对测量精度影响Fig. 3　Localization precision as time measurement error is 0.5 ms

针对鱼雷入水点实时测量无法获取时， 文中给出了时延差双曲面定位的方法， 并利用海上实测数据对该方法进行了验证， 讨论引入浮标阵测时误差时定位精度受到的影响， 从中得出如下结论。1） 鱼雷入水点、出水点等在原始信号中明显， 可计算不同浮标间的时延差， 从而可采用时延差双曲面法进行定位。2） 由于人工引入的测时误差对测量的影响较小， 在浮标阵内测量误差最大不超过4 m。

［1］ 熊乾坤， 唐世轩. 一种鱼雷主动声自导目标检测真实性判定方法［J］. 鱼雷技术， 2015， 34（2）： 104-107.

Xiong Qian-kun， Tang Shi-xuan. A Facticity Judgment Method for Target Detection of Torpedo Active Acoustic Homing［J］. Torpedo Technology， 2015， 34（2）： 104-107.

［2］ 付进. 长基线定位信号处理若干关键技术研究［M］. 哈尔滨： 哈尔滨工程大学， 2007.

［3］ 田坦. 水下定位与导航技术［M］. 北京： 国防工业出版社， 2007.

［4］ 戎晓政， 刘加. 声源定位中的时延估计方法研究［J］. 电声技术， 2010， 34（2）： 42-46

Rong Xiao-zheng， Liu Jia. Research on Time Delay Estimation Methods in Source Location［J］. Audio Engineering， 2010， 34（2）： 42-46.

［5］ 蔡德军， 胡涛. 时延估计技术及其在多途环境中的应用［J］. 声学学报， 2001， 26（1）： 34-40.

Cai De-jun， Hu Tao. Time-delay Estimation and Its Application in Multipath Environment［J］. Acta Acustica， 2001，26（1）： 34-40.

（责任编辑： 杨力军）

Application of Localization Method Based on Time Delay Difference and Hyperboloid to Torpedo Water-Entry Point Measurement

LI Wei-hua，XUE Fei，MA Jin-yin
（91439thUnit， The People′s Liberation Army Of China， Dalian 116041， China）

To measure torpedo water-entry point in real time， a localization method of time delay difference and hyperboloid based on multiple array is proposed. This method can measure the geodetic coordinates of a target with the precision of 10 m（standard error） without needing the azimuth of vector. The influence of time measurement error of buoy array on localization precision is discussed， and the result shows that the maximum measurement error in the buoy array is no more than 4 m.This method is verified by sea trial.

torpedo； time delay difference； hyperboloid； buoy array

TJ630.34献标识码: A

1673-1948（2015）06-0420-03

10.11993/j.issn.1673-1948.2015.06.005

2015-08-19；

2015-09-08.

李韦华（1987-）， 男， 硕士， 工程师， 主要研究方向为水声测量.