曲阜市尼山水库年降雨量预测分析

景晓林，颜桂杰，霍孟娥

（曲阜市尼山水库管理局，山东 曲阜 273100）

近年来，人们对水资源量的需求越来越大，降雨量作为水资源的重要来源之一，关系到一个地区工农业的发展。由于降雨量受多种因素的影响，降雨过程具有随机性，对区域降雨量进行较为准确的预测分析，有助于当地水利部门提前制定相应的防洪抗旱措施，对保护人民群众的生命安全和提高工农业生产效益有着重要意义。

1 加权马尔科夫链预测步骤

1）根据资料序列，求出指标值平均值和样本均方差，并对指标值进行分级，从而确定马尔科夫链的状态空间，即 E=｛1， 2，…，m ｝。 然后根据分级标准确定资料序列中各指标值的状态。

2）对资料序列进行统计，根据不同步长指标值转移概率，列出马尔科夫链的转移概率矩阵。

3）根据得到的转移概率矩阵，进行各行各列加和得到边缘矩阵，进一步检验该序列是否符合马尔科夫链性质。

4）计算指标值各阶自相关系数，公式为：

其中：rk为滞时为k（k∈E）年的自相关系数；n为资料序列长度；xi为第i时段的指标值；为指标值的平均值。

对rk进行规范化处理，得到各步长的马尔科夫链的权重。公式为：

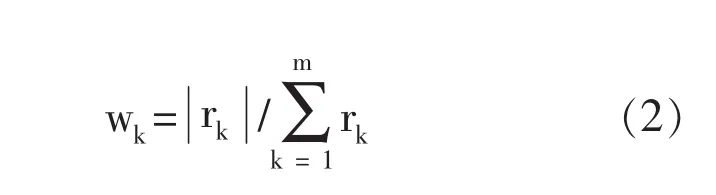
其中：m为预测时需要计算的最大步长。

5）计算不同步长的马尔科夫链的状态矩阵，并以前面各时段的指标值为初始值，来预测该时段指标值的状态概率。

6）对各预测概率进行加权处理，即

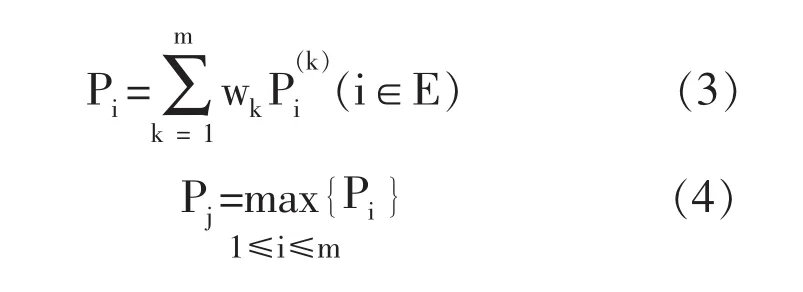
Pj中时刻j即为预测时段指标值的预测状态。

7）分析马尔科夫链的平稳分布和遍历性。

2 实例应用

本文选取尼山水库 1960—2014年 （因1996—1999年，尼山大坝大规模翻修，观测设施被破坏，1997年、1999年数据未测）共53年的降雨量资料为例，预测尼山水库2015年的降雨量。先以1960—2013年（不包括1997年、1999年）降雨序列预测2014年降雨量状况。

1）根据1960—2013年 （不包括1997年、1999年）降雨量计算得到：降雨量序列平均值744.32 mm，标准差 s=221.57 mm，取 α1=1.1，α2=0.5，将该降雨量序列划分为5个级别，如表1。

表1 年降雨量分级表

2）经统计，根据不同步长指标值转移概率，得到马尔科夫链的转移概率矩阵如下（以步长为1的频数转移矩阵及状态转移概率矩阵为例）：同理可得到步长为2～5的状态转移概率矩阵。

3）根据得到的步长为1的频数转移矩阵及转移概率矩阵，检验该序列的马氏性。其中给定显著性水平 α=0.05，查表得到因此认为该序列符合马氏性。

4）根据公式（1）、（2），计算指标值各阶自相关系数rk及标准化的马尔科夫链权重，如表2。

表2 1～5阶各阶自相关系数及其权重

5）以2009—2013年的降雨量及其相应的状态转移概率矩阵，预测2014年降雨量，可知2014年降雨量预测状态为3，即平水年 （633.53 mm

同理，根据步骤 1）～5），以 1960—2014 年（不包括1997年、1999年）的年降雨量序列预测2015年的降雨量状况，可知2015年降雨量预测状态为 3，即平水年（633.19 mm

6）马尔科夫链的平稳分布和遍历性分析。以相依性最强的步长为3的马尔科夫链特征分析。该马尔科夫链的5个状态是相互连通的，而且是非周期的，因此该链是不可约的，从而可知该链的5个状态是正常返的。由马尔科夫链理论该链具有遍历性，且存在唯一的平稳分布（即此链的极限分布）。其求解方程组为：

根据步长为3的状态转移矩阵，得到平稳分布与各状态重现期，如表3。

表3 平稳分布与各状态重现期

结合表3和本文的分级标准，尼山水库在1960—2014年（不包括1997年、1999年）53年的降雨序列中平水年出现的概率最大，平均每隔2.59年出现一次，概率为38.6%；偏丰年出现的概率最小，平均每隔7.46年才出现一次，概率为13.4%。

3 结语

根据尼山水库1960—2014年降雨资料，建立了加权马尔科夫链模型，验证了该序列的马氏性和可靠性，预测出尼山水库2015年降雨量状态为平水年，年降雨量在633.19 mm

根据马尔科夫链遍历性理论，求出了该降雨序列的平稳分布，得出尼山水库年降雨量出现平水年的可能性最大，概率为38.6%。