双重非均匀性对燃耗计算影响的初步分析

秦冬 巨海涛 强胜龙 倪东洋 魏彦琴

摘 要：弥散燃料是一种先进的燃料元件形式，具有承受燃耗深、包容裂变产物能力强和导热性好的优点。弥散燃料栅元在栅格非均匀性之外引入了燃料芯体的非均匀性，具有双重非均匀的特性。为了控制栅元反应性，燃料芯体中可能会布置一定量的可燃毒物颗粒。在计算含有可燃毒物颗粒的弥散燃料时，如果对燃料芯体采取均匀化混合处理的方式，有可能高估可燃毒物的吸收，造成一定的计算偏差。该文基于弥散型燃料，使用MOI程序对单板栅元模型进行了计算，初步分析了双重非均匀性对燃耗计算的影响。

关键词：双重非均匀性 燃毒物颗粒 燃耗计算

中图分类号：TL333 文献标识码：A 文章编号：1674-098X（2015）08（c）-0247-03

Preliminary Analysis of Double Heterogeneity Effects on Burnup calculation

Qin Dong Ju Haitao Qiang Shenglong Ni Dongyang Wei Yanqin

（Science and Technology on Reactor System Design Technology Laboratory，Nuclear Power Institute of China，Chengdu Sichuan，610041，China）

Abstract：The dispersion fuel is an advanced fuel element form，which has advantages of high burnup，strong ability of containing fission products and good thermal conductivity. The dispersion fuel cell has both lattice heterogeneity and fuel core heterogeneity，which has an intrinsic characteristic of double heterogeneity.And a certain amount of burnable poison particles can be arranged in the fuel core in order to control the reactivity.If calculating dispersion fuel with burnable poison particles in a homogeneous way，the absorption will be over evaluated and a certain deviation will be introduced.This paper studies the double heterogeneity effect on burnup calculation in dispersion fuel element with MOI code.

Key Words：Double Heterogeneity；Burnable Poison Particle；Burnup Calculation

弥散燃料是一种先进的燃料元件形式，它由燃料颗粒（U、Pu的化合物）弥散分布在惰性基体材料（如金属、陶瓷或者石墨等非裂变材料）中构成。弥散型燃料元件在一般非均匀性（燃料芯体、包壳、慢化剂或冷却剂）之外引入了新的非均匀性，即燃料芯体的非均匀性（燃料颗粒、可燃毒物颗粒弥散分布在基体材料中），形成燃料元件的双重非均匀性。对于此类燃料特别是在含有可燃毒物颗粒的情况下，如果仍然采取工程上常用的均匀化混合处理的方式，即将燃料及可燃毒物颗粒和基体材料均匀化混合，有可能高估可燃毒物的吸收，造成一定的计算偏差[1]。

该文基于弥散型燃料，使用MOI程序对弥散燃料单板栅元模型进行了计算，初步分析了双重非均匀性对燃耗计算的影响。

1 研究内容

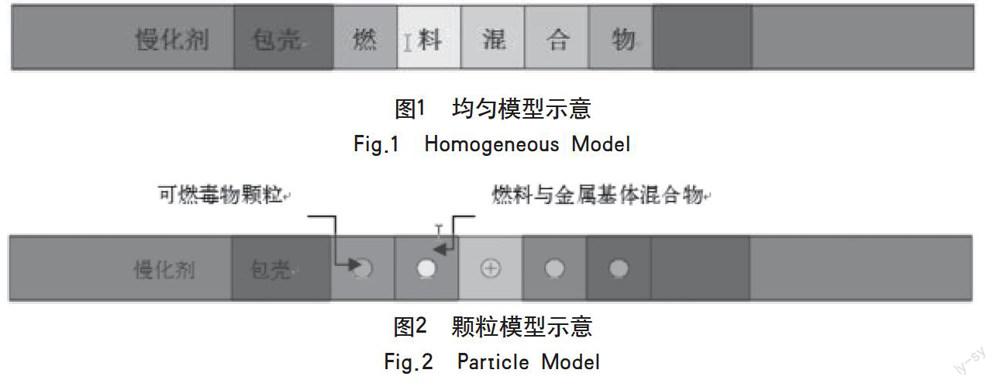
研究基于单板燃料栅元，栅元可分为燃料芯体、包壳和慢化剂三部分。其中燃料芯体是弥散在金属基体中的UO2以及硼可燃毒物颗粒。在实际计算建模时，对栅元芯体采用两种处理方式：（1）认为UO2颗粒、可燃毒物颗粒以及金属基体均匀混合，形成单一混合物材料，不妨将该计算模型称为均匀模型，模型示意见图1所示；（2）将UO2和金属基体材料均匀混合（计算表明，UO2颗粒的双重非均匀效应对计算结果影响较小，本次不做考虑），认为可燃毒物颗粒独立存在（可燃毒物颗粒作为一个独立燃耗区），不妨将该计算模型称为颗粒模型，模型示意如2所示。

2 MOI程序

MOI[2，3]程序系统是基于连续能量蒙特卡罗方法开发的堆芯燃耗计算程序，可在UNIX或LINUX平台下运行，可以实现并行的调棒临界燃耗计算，具有蒙特卡罗方法可处理任意几何、异性散射、任意边界条件等优点，其基本流程如图3所示。同时MOI采用了独特的混合燃耗计算模式，可计算多种类型可燃毒物（包括弥散的可燃毒物颗粒），并且该软件具有较高的燃耗计算精度，适用于该文的研究。

3 计算结果分析

3.1 均匀模型与颗粒模型比较

弥散燃料单板栅元的均匀模型与颗粒模型燃耗计算结果如图4所示。从图中可見，均匀模型和颗粒模型的单板栅元Kinf随燃耗变化的趋势基本一致，但在燃耗初期以及燃耗中期有一定的计算偏差。燃耗初期均匀模型Kinf偏小，与颗粒模型相比相对偏差接近-5.0%。这是因为均匀模型中将可燃毒物与燃料混合处理，高估了可燃毒物对中子的吸收；燃耗中期均匀模型Kinf偏大，与颗粒模型Kinf的相对偏差约2.0%。总体上看，均匀模型与颗粒模型Kinf相对计算偏差呈现从负到正，再逼近零的变化。相对计算偏差由负变正的燃耗时刻约在30000 MWD/tU左右，出现最大正值的燃耗时刻约在60000 MWD/tU左右。

不同计算模型B-10核子密度随燃耗的变化见图5所示。从图5中可见，不同计算模型B-10核子密度随燃耗增加单调递减。但颗粒模型与均匀模型B-10核子密度的差随燃耗增加出现了先增加后减少的现象。可燃毒物核子密度差值最大时刻约在30000 MWD/tU左右，对于Kinf而言是计算相对偏差从负变正的时候。

由于可燃毒物热中子吸收截面很大，随着燃耗的进行可燃毒物消耗很快，自屏效应也会随之削弱的比较快，因此，这两种模型计算的Kinf应会不断接近，最终相对偏差趋于零。但从计算结果看，这两种模型所计算的Kinf的相对偏差并不是直接逐渐逼近零，而是先从-5.0%逐渐变为+2.0%，然后从+2.0%逐渐逼近零。出现这种现象的原因是由于自屏效应引起的可燃毒物消耗速度不一样。

为了便于描述，定义如下参数：N均为均匀模型中B-10核子密度；σ均为均匀模型中B-10微观吸收截面；N颗为颗粒模型中B-10核子密度；σ颗为颗粒模型中B-10微观吸收截面。

均匀模型中B-10在燃料芯体中均匀分布，最大程度弱化了B-10的自屏效应，即σ均>σ颗，使得B-10核子密度消耗较快，即N均递减较快，那么均匀模型中B-10的总吸收Σ均=N均（↓快）×σ均（↑变大，速度较慢），从而Kinf增加也较快。

颗粒模型存在自屏效应，使得B-10的等效微观吸收截面较小，进而B-10的消耗要慢于均匀模型；但随着燃耗的加深，自屏效应减弱，使得颗粒模型中B-10的微观吸收截面逐渐增加（但仍小于均匀模型），进而使得B-10消耗也逐渐加快，即颗粒模型中B-10的总吸收Σ颗=N颗（↓慢）×σ颗（↑变大，速度较快），从而Kinf的增加要慢于均匀模型。

根据以上两点，可以初步得出以下关系：

初始时刻：σ均>σ颗，N均=N颗，因而均匀模型的Kinf与颗粒模型的计算偏差较大。

燃耗过程中：σ均>σ颗，N均

燃耗末期末：σ均≈σ颗，N均≈N颗，因而Kinf和B-10核子密度计算偏差均约等于零。

3.2 质量修正的燃耗初步分析

含弥散可燃毒物颗粒的燃料芯体，必须采用颗粒模型才能较为准确的进行计算，而目前一般的栅元计算程序无法进行颗粒模型的建模，难以考虑双重非均匀性，因此，若继续使用均匀模型计算则必须考虑一定的修正。

引入可燃毒物的自屏因子[4]，它的定义为：

由此可见，可燃毒物有效吸收截面為：

对于可燃毒物总吸收截面，有：

由于MOI程序使用点截面库，对可燃毒物吸收截面使用修正因子可等效视为对毒物核子数量使用修正因子。引入修正因子使得燃耗初期Kinf与颗粒模型计算结果一致，并继续进行燃耗计算。修正均匀模型与颗粒模型计算的Kinf随燃耗变化见图6所示。从图6中可见，燃耗初期和燃耗末期的Kinf相对偏差均为零左右。燃耗初期Kinf相对偏差较小主要是因为引入了修正因子，使得均匀模型计算时吸收减小。燃耗末期Kinf相对偏差较小主要是因为可燃毒物已基本全部消耗，自屏效应已完全消失。但是在燃耗中期附近，修正均匀模型的Kinf比颗粒模型大4%左右。这种变化趋势和B-10的核子数量变化相关。由于采用了质量修正，这两个模型的B-10初始核子数量并不一致，因此，进行归一化处理。归一化后两模型B-10核子密度差值及Kinf相对偏差随燃耗的变化见图7所示。从图7中可见归一化B-10核子密度差值及Kinf相对偏差随燃耗的变化曲线从形态上是一致的，只是出现极值的燃耗时刻有些差别。

从上述结果看，质量修正能够在燃耗初使得均匀模型的Kinf计算结果与颗粒模型一致，但是这种修正在燃耗中期会带来较大的计算偏差。

4 结语

该文基于MOI程序，对弥散燃料单板栅元进行了均匀模型和颗粒模型建模计算，初步分析了双重非均匀性对燃耗计算的影响，可以得到以下结论。

（1）双重非均匀性的存在使得含有弥散可燃毒物的栅元Kinf在燃耗初期和燃耗中期出现一定的计算偏差。

（2）如果引入的修正因子不随燃耗变化，在燃耗中期会高估栅元Kinf，因此，在修正时必须考虑修正因子随燃耗变化。

参考文献

[1] 常鸿，杨永伟，经荣清.球床式高温气冷堆初次临界物理计算的蒙特卡罗方法模型分析[J].核动力工程，2005，26（5）：419-424.

[2] 强胜龙，秦冬，柴晓明，等.PWR堆芯中弥散型可燃毒物的燃耗特性研究[J].核动力工程，2014，35（2）：1-4.

[3] 强胜龙，秦冬，柴晓明，等.基于蒙卡方法的燃耗计算误差研究[J].原子能科学技术，2014，48（12）：2321-2325.

[4] 谢仲生，吴宏春，张少泓.核反应堆物理分析（修订版）[M].西安交通大学出版社，2004：220.