初始状态对自组织演化过程的影响

苏亚凤，李普选，徐忠锋，张孝林

（西安交通大学，陕西西安 710049）

初始状态对自组织演化过程的影响

苏亚凤，李普选，徐忠锋，张孝林

（西安交通大学，陕西西安 710049）

从实验上系统研究了在强电场下处于介质中的大量金属小球从不同初始状态通过自组织演化为分形的过程；用Sandbox方法定量分析了最终形成的稳定树枝状分形的维数。结果表明:不同初始状态形成分形的过程完全不同，但最终的树枝状分形的维数基本相同。分析认为，小球之间的相互作用存在临界作用距离，不同初始状态相邻小球之间的平均间距不同，因而演化过程不同；而维数相同正是系统耗散相同的体现。

自组织；分形；Sandbox方法；分维数

自组织是指开放系统在远离平衡的条件下，在一定的外部因素作用下自发地由无序走向有序的过程。自组织现象广泛存在于自然界中，例如宇宙正在从原有的混沌状态演化成一个生机勃勃的大自然；生物体的成长与功能的进化；天空中规则的“云街”的形成；晶体的沉积和生长等都属于自组织［1-3］。近30多年来，在实验上发现并研究了很多有趣的自组织的过程，如枝晶的可控生长［4］、金属气体沉积［5］、电化学金属沉积［6-9］、处于电场中的大量粒子运动行为［10-12］等。但未见对自组织过程随初始状态演化过程不同作系统报道。

实验小组曾实时拍摄了大量金属小球在强电场下形成的树枝状分形的过程，并研究了分形维数与所加电压的变化关系，发现电压越高，形成的分形维数越小［12］。进一步系统研究了小球从紧密聚集的初始状态和不同随机离散分布的初始状态通过不同的自组织演化形成分形的过程，发现了完全不同于文献［11］所描述的形成过程，并分析了不同初始状态对应不同自组织演化过程的原因；定量分析了分形维数与初始状态的关系。此研究对金属气体沉积、金属电化学沉积过程、超分子凝聚等自组织过程的研究具有借鉴意义。

1　实 验

1.1实验装置

实验装置在文献［12］中有详细说明，现简述如下:如图1所示，处于中央位置的阳极为带有尖端的金属细杆，阴极是宽为1 cm、围绕在直径为15 cm的盘状玻璃皿外围的铜带。两极电压被限制在10～11 kV间。盘中金属小球是半径为1.5 mm，质量约为111 mg的光滑不锈钢球。金属小球被置于蓖麻油介质中，介质高度以浸没小球为宜。图中所示的视频摄像装置与计算机连接，可以即时记录实验的整个过程。

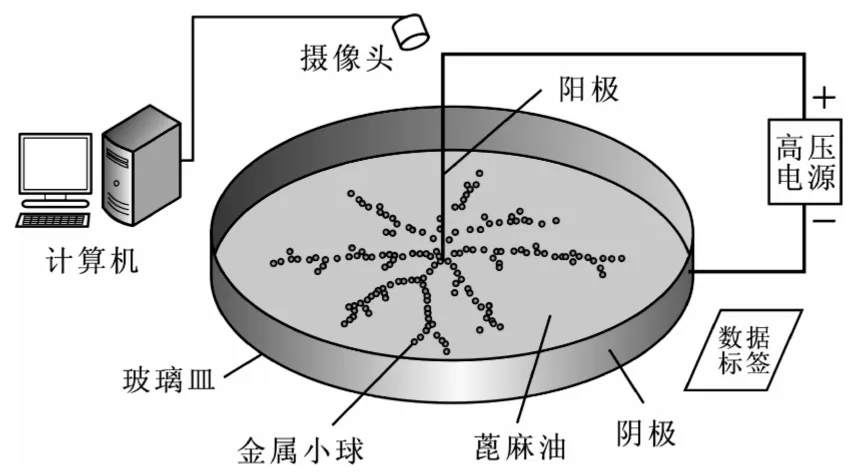
图1　实验装置

1.2实验过程

（1）依照图1连接电路及摄像装置。将小球以聚集的状态平铺于阳极周围，形状大约为圆形。

（2）打开视频记录，接通高压电源，调节电压，观察小球运动行为；待小球达到稳定状态后，断开电源，停止视频记录。

（3）依照（1）和（2）的过程，拍摄小球初始状态为各种随机离散分布时的自组织演化过程。

2　实验结果及分析

2.1不同初始状态的小球自组织演化过程

通过多次实验，发现强电场下处于介质中的金属小球的运动行为均呈典型的自组织演化过程。为了对比，研究了在实验条件大体相同、而小球初始状态不同时的自组织演化过程。图2所示为温度大约为18～20℃、电压为11 kV的条件下密集堆积成圆形状的200个金属小球通过自组织形成分形的整个过程。接通电源后，在0～1 s内，小球几乎同时迅速向四周运动，并连成有分支的串状，如图2中（a）～（b）所示。在1～5 s内，小球继续逐渐向四周挪动，到5s时小球已经全部分开，并相互连接成树枝状结构，见图2（b）～（c）。在5～80 s内，树枝状结构逐渐扩展长大，但整体形态基本不变，如图2（d）～（g）。随着时间的推移，小球进一步分散开，但树枝状结构基本未变，在大约122秒时形成最终的稳定的分形结构，如图2（h）所示。

图2　初始状态为密集放置时小球随时间的演化过程

图3为温度大约为30～31℃、电压为10 kV条件下拍摄的200个金属小球随机分散放置时通过自组织过程形成分形的整个过程。实验发现:接通电源的瞬间，最靠近中央阳极的金属小球首先被推搡与其邻近小球连接成串状，被连接的小球再与自己最靠近的小球相互连接，见图3（a）～（b）。在10s的时间内，连接体已经发展到最外围的小球，如图3（c）所示。此后时间内，连接起来的部分缓缓蠕动吸收其邻近的其它小球，使连接体缓慢扩张，见图3（c）～（d）。其间，连接体的枝头如蠕虫一样左右运动，并将离散的小球吸引至最近的分枝中，树枝状结构逐渐显现出来，见图3（d）～（g）。图3 （g）～（h）显示形成的树枝状结构枝头继续做类蠕虫运动，俘获邻近离散的小球加入，同时整体向四周伸展生长，大约在87 s时整个系统达到了一个稳定状态，见图3（h）所示。

图3　初始状态为随机离散放置时小球随时间演化过程

进一步研究了小球从密到疏逐渐变化随机放置的演化过程。实验发现:初始状态不同，自组织过程不同。若初始状态为密集放置，小球几乎同时运动来参与分形的形成过程（见对图2所述）；而最疏散放置的情况，则自组织大致是从中央阳极处的小球运动开始、到边缘形成串状后，再做类蠕虫运动，逐渐纳入两边小球，次序是由近及远、逐步扩大，形成树枝状结构。初始状态介于密集和最疏散放置中间的，则形成过程也介于以上二者之间，即既存在同时运动的一些小球，也存在由中央向边缘依次连接并吸收邻近小球的现象。

虽然形成过程不同，但形成的最终稳定的树枝状结构很相似，如图4所示，其中，（a）～（f）均为初始状态图，（a′）～（f′）为各自对应的最终稳定分形结构。我们的实验温度就是环境温度，图（a′）～（c′）是在温度为18～20℃、电压为11 kV的条件下的实验照片，图（d′）～（f′）是在温度为30～31℃、电压为10 kV的条件下拍摄的最终稳定形态。可以看出，图（a′）～（c′）三图小球形成的树枝状结构非常相似；与图（d′）～（f′）也很相似，但图（d′）～（f′）相对（a′）～（c′）图比较分散。

图4　不同初始状态及其对应的最终树枝状结构：图（a）～（f）均为初始状态，图（a′）～（f′）为各自对应的最终树枝状结构

2.2演化过程不同原因分析

处于蓖麻油中的小球不仅受静电力的作用，还受到油的粘滞阻力的作用。若小球开始运动，两球之间的静电力必须大于油的静粘滞阻力。实验和理论表明［13-15］，电场越强，处于电介质中两小球的静电相互作用力越大；两小球之间的间距越小，两小球的静电相互作用力也越大。因此对应一个电场，存在一个临界作用距离，小于此距离，小球之间由于静电相互吸引会产生相对运动，大于此距离，则小球不会运动；而电场越强，临界作用距离越大。实验中从中央阳极到周缘阴极，电场基本呈辐射状递减趋势，因此临界作用距离从中央到周缘是从大到小递减变化的。对图2 （a）所示的聚集初始状态，小球相互紧靠围绕在阳极周围，间距均小于临界作用距离。因此，一旦加上电压，所有小球同时相互吸引作用，小球间介质被击穿而同时带上正电荷，因静电排斥而同时向四周运动。在此后的时间内是已经形成的分形的长大过程。而对图3（a）所示的小球疏散随机放置的初始状态，由于靠近中央位置处电场较强，临界作用距离较大，因此在中央位置附近间距小于此位置的临界作用距离的小球迅速连接起来，并逐渐吸收在临界作用距离以内的其它小球，小球串逐渐加长，且出现分枝。当连接体到达边缘时，串之间由于存在相互作用而出现类蠕虫运动，伴随者与邻近小球距离的变化，逐渐俘获了进入临界作用距离范围内的小球，根据作用力的不同或纳进小球串，或使其成为小球串的分枝。直到将临界作用距离范围内的所有小球吸收为止。图3（h）中剩余的离散小球位于临界作用距离以外，因此没有被链条俘获。初始小球平均间距介于密集（如图4（a））和最疏散放置（如图4（f））中间的，即既存在一些小球同时运动，也存在由中央向边缘依次连接并吸收邻近小球的运动过程。

2.3分形维数的计算

分形是具有扩展对称性的自相似结构，在几何性质上可以用分维数表示。我们利用Sandbox法［16］计算了所形成的分形的维数。由于分形由中心向四周生长，且只有一个生长中心，因此计算维数时盒取为圆形，圆心选在生长中心处，如图5所示。由于圆中象素数目与小球数目成正比，因此只需要数出各圆中的小球数目N，量出各圆的直径d（或半径），计算出lnN和lnd，做出lnN与lnd关系曲线，相应的拟合直线斜率即为图形的分形维数D。

图5　稳定的树枝状结构和Sandbox法

2.4不同初始状态演化形成的分形维数分析

对图4（a′）～（f′）图分别取类似于图5的不同直径的圆盒，其中对图4（f′）中圆盒未取类似于（d′）和（e′）中的最小圆盒的原因是其内部存在离散的金属小球，这些小球一开始处于与邻近小球距离大于临界作用距离以外的位置而未参与形成树枝状结构，因此圆盒取得较大些，分别数出各圆盒对应的小球数目。图（6）是用Matlab计算出的相应的小球数目对数与各圆盒直径对数的关系图。可以看出，每一个图中二者是相关性较好的直线关系，符合分形的最基本特征，直线的斜率即为分形的维数。

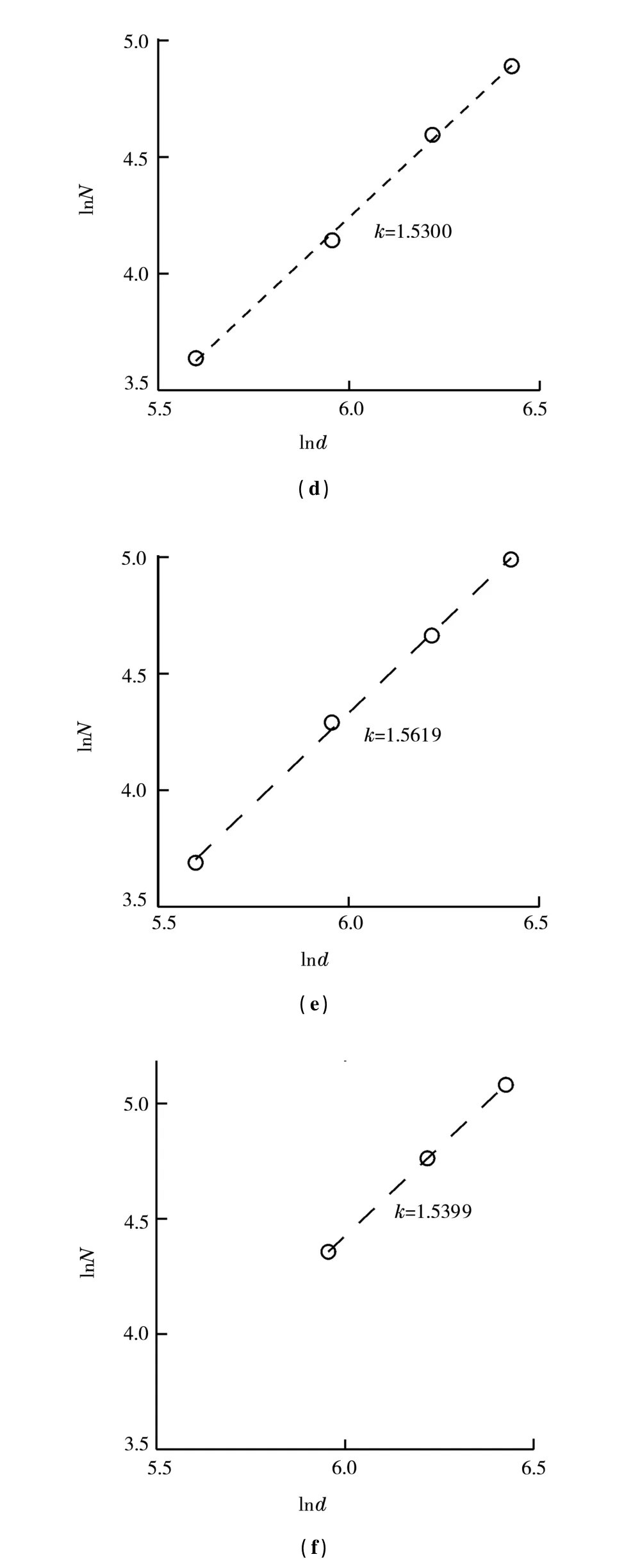
图6　盒直径和小球数目的对数图及拟合直线的斜率

图6是计算出的图4（a′）～（f′）的相应的小球数目对数与各圆盒直径对数的关系图。可以看出，每一个图中二者是相关性较好的直线关系，符合分形的最基本特征，直线的斜率即为分形的维数。图4中（a′）～（c′）图分维数约为1.76，图4（d′）～（f′）图分维数在1.54左右，而图4（a′）～（c′）与图4（d′）～（f′）实验条件稍有差异（见3.1节），分维数也是稍有差异，仅差0.2左右。这个实验结果表明，不管是从聚集态的自组织演化，还是从随机离散态自组织演化，也不管离散的小球间的间距在一定范围内如何变化，所得的稳定形态有着相似的结构，其统计结果是基本相同的，即分维数大致相同。分形维数也描述了系统的耗散，实验条件相同时，耗散相同，导致分维数相同。不同微观形态的分维数相同，意味着其遵循着相同的统计规律，此实验充分体现了耗散结构多样性与规律性的统一。

需要说明的是，此实验对环境温度很敏感。这里出现的电压越大分维数反而较大，与文献［12］中报导的结论不同的原因是:两组实验的温度不同，相差10℃以上，电压较大的温度较低，导致其蓖麻油的粘滞性较大，小球分散程度低，因而分维数稍高些。

3　结 论

处于强静电场下的大量金属小球初始状态不同，自组织演化过程不同。聚集的初始状态，所有小球几乎同时相互作用，参与形成分形，再一起扩展；小球离散随机放置的初始状态，则是处于临界作用距离以内的部分小球先聚集在一起，形成串状或带分枝的串状做类蠕虫运动，再将邻近小球依次纳入，逐渐形成分形。

虽然不同初始状态自组织演化过程不同，但最终均呈现为稳定的树枝状结构，且其分维数基本相同。原因是相同实验条件下系统的耗散相同，导致描述系统耗散的分维数相同。本实验结果有利于理解金属沉积和超分子凝聚过程中的簇团聚等现象。

［1］ 徐孺英.横断学科简论［M］.济南:山东大学出版社，1990.326.

［2］ Francesc SagueHs，Marta Queralt LoH pez-Salvans，JosepClaret.Growthandformsinquasi-twodimensionalelectrocrystallization［J］.Physics Reports，2000，337:97-115.

［3］ 彭英才，池田弥央，宫崎诚一.Si纳米量子点的LPCVD自组织化形成及其生长机理研究［J］.物理学报，2003，52（12）:3108-3113.

［4］ Sawada Yasuji，Dougherty A，Gollub J P.Dendritic and fractal patterns in electrolytic metal deposits［J］.Phys Rev Lett，1986，56（12）:1260-1263.

［5］ Hu L，Liu B X，Effect of chemical and magnetic interactions on fractal growth under deposition-diffusion -aggregation in some binary metal systems［J］.Appl Phys A，2004，78:397-400.

［6］ Brady R M，Ball R C.Fractal growth of copper electrodeposits［J］.Nature，1984，309（17）:225-229.

［7］ Mukherjee M，Saha S K，Chakravorty D.Fractal growth of silver nanoclusters in a polymer medium［J］.Appl Phys Lett，1993，63（1）:42-44.

［8］ Sun B，Zou X W，Jin Z Z.Morphological evolution in the electrodeposition of the Pb-Sn binary system［J］. Phys Rev E，2004，69:067202-1-4.

［9］ Zhang M Z，Zuo G H，Zong Z C，et al.Self-assembly from the branch pattern to parallel wire array in electrodeposition［J］.Appl Phys Lett，2006，88:203106-1-3.

［10］Wen W J，Lu K Q.Electric-field-induced diffusion-limited aggregation［J］.Phys Rev E，1997，55（3）: R2100-R2103.

［11］JUN Joseph K，HUBLER Alfred H.Formation and structure of ramified charge transportation networks in an electromechanical system［J］.PNAS，2005，102 （3）:536-540.

［12］苏亚凤，李普选，陈鹏，等.树状分形结构形成过程的实验研究［J］.物理学报，2009，58（7）: 4531-4535.

［13］Wang Zhiyong，Peng Zheng，Lu Kunquan，et al.Experimental investigation for field-induced interaction force of two spheres［J］.Appl Phys Lett，2003，82（11）: 1796-1798.

［14］Wang Zhiyong，Shen Rong，Niu Xiaojuan，et al.Frequency dependence of a field-induced force between two high dielectric spheres in various fluid media［J］. J Appl Phys，2003，94（12）:7832-7834.

［15］Tao R，Jiang Qi，Sim H K.Finite-element analysis of electrostaticinteractionsinelectrorheologicalfluids ［J］.Phys Rev E，1995，52（3）:2727-2735.

［16］孙霞，吴自勤，黄畇.分形原理及应用［M］.合肥:中国科学技术大学出版社，2003，42-43.

Influence of Experimental Initial State on the Process of Self-organization Evolution

SU Ya-feng，LI Pu-xuan，XU Zhong-feng，ZHANG Xiao-lin
（Xi’an Jiaotong University，Shaanxi Xi’an 710049）

The self-organization evolution processes of large-number metallic balls from different initial states to the fractal structures are observed systematically under high voltage.The fractal dimensions of final stable dendritic fractal structures are calculated by the sandbox method.The result shows that although the self-organization evolution processes are quite different with different initial states，their fractal dimensions are almost the same.Our analysis suggests that there exists a critical interaction distance between metal balls，the averaged distances between neighboring balls are different in different initial states which result in different evolution processes，while the same fractal dimension reflects the direct embodiment of the same dissipation of the system.

self-organization evolution；fractal；sandbox method；fractal dimension

O415.3

A

10.14139/j.cnki.cn22-1228.2015.02.017

1007-2934（2015）02-0060-06

2014-11-03

西安交通大学教师发展中心教改重点项目（08129006）

∗通讯联系人