渗流相变实验

李 阳，左 颖，赵玉连，周长宏

（天津农学院，天津 300384）

渗流相变实验

李 阳，左 颖，赵玉连，周长宏

（天津农学院，天津 300384）

基于渗流相变理论设计了可重复使用的渗流实验仪器。在大学物理甚至高中物理一次实验课的时间内，利用渗流实验仪进行测量不同随机占据概率下的电流，对四次实验结果进行平均后，绘制相对电导率与占据概率曲线，可以获得与文献［9］相似的结果，再现渗流相变的存在。

渗流相变；占据概率；电导率

渗流理论诞生于上世纪50年代，其后在理论和应用上都得到飞速的发展［1］。在理论方面，人们通过解析计算和计算机模拟获得不同晶格上的临界渗流概率［1］，其中正方晶格上点渗流的临界占据概率为pc=0.592746。在应用方面，疾病的传播［2］、水或污染物在土壤中的渗透［3］、以及热力学相变的几何解释［4-5］等均可看到渗流理论的应用。为了增加渗流相变的直观性，不少物理教育工作者都尝试用不同的方法演示渗流相变的存在［5-8］。这些演示方法大多基于1971年Last和Thouless渗流相变实验研究［9］。Last和Thouless通过在导电纸上随机去掉一些空隙，从而实现占据概率逐渐减小的物理过程。每一次去除的小空隙的随机性借助随机数表确定该次去除空隙的坐标实现。当占据概率每减小一个百分点时，测量导电纸一组对边的电导率。在图形上作出σp/σ1-p的图形，可以确定渗流临界概率。但这些实验方法没有排除一次实验中坐标重复的点，同时也缺乏实验的可重复性。为此我们通过利用均匀打孔且相邻孔被铜丝相连的有机板和随机数表构造可重复利用的渗流实验仪，让学生可以在一次大学物理甚至高中物理实验课上了解渗流相变和渗流集团的存在，并初步了解关键占据格点在渗流集团中的重要性等。

1　渗流相变介绍及实验原理

渗流理论可以通过考虑由N个格点和M条边构成的正方晶格G占据情况来说明。如果我们考虑点渗流，则正方晶格G的M条边均处于连通状态，则随着格点占据概率p取值由1逐渐减小，对无限大格子G，将会在pc=0.592 746时，系统中没有连通格子G两对边的占据格点集团存在。如果占据格点和边都是导体，则意味着在p ＞pc时，晶格G两端如果加上电压，将会有电流从晶格一端流到另一端，而当p≤pc，电流将不能从一端流到另一端。这种随着占据概率p这一参数的变化，晶格两端电流从有到无的转变，在物理上常称为渗流相变，或几何相变［10-11］。它是最为简单的连续相变，因此是研究相变和临界现象得力的模型之一［1，11］。如果我们考虑键（边）渗流，则正方晶格G的N个格点均处于占据状态，随着边连通概率p的取值由1逐渐变小，无限大的晶格G将在pc=1/2时出现渗流相变。本实验主要考虑点渗流。

图1为计算机模拟20×20正方形格子上不同占据概率下的位形图。图中每一格点用一小正方形表示，如果该格点没有被占据，则在图中用白色标志。如果被占据，则用非白色的颜色标志。如果相邻格点被占据，则认为属于同一格点，用同一颜色表示。我们从图上看出，随着占据格点逐渐减少，贯穿整个格子的上下或左右边界黑色表示的集团会逐渐瘦小并消失。这样的集团称为渗流集团。如果把每一格点想象为一个电键，则在格子的两边加上电势差后，渗流集团中会有电流通过。可用渗流相变实验实现类似过程。

图1　计算机模拟20×20正方形格子上不同占据概率下的随机占据位形图

在实验中，我们利用有机玻璃作为支撑平台，在该玻璃上按一定距离（本文实验用的有机玻璃板相邻孔中心距离为1.4 cm）打出半径恰当（本文实验红的有机玻璃板上小孔半径为0.2 cm）的小孔，多股细铜丝经搓揉后将相邻小孔连接起来。用导体小球作为电键来连同相邻小孔之间的电路。当小孔被导体小球随机占据时，该体系转化为随机电阻网络。设小孔总数为N0=L×L，（本文实验中取L=16），打印一张L×L的两位数随机数表，每一个随机数对应有机玻璃板上的一个小孔。在初始阶段，将小球填充所有的小孔，则占据概率p=1。如果将随机数表中数值大于X（如取值90）的对应小孔中的导体小球取出，则此时占据概率为

如果在该有机玻璃对边a，b施加恒定电势差Uab，则可利用电流计测得流过该随机电阻网络的电流I。利用电势差与电流和导体电阻间关系，得该随机电阻网络电导为

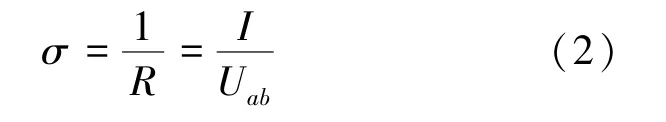
设所有小孔均被导体小球占据，即点占据概率p=1时，测得电流强度为I1，相应的电导为σ1，则格点占据概率为p时，随机电阻网络的电导σp与σ1的比值称为相对电导，是一个无量纲数:

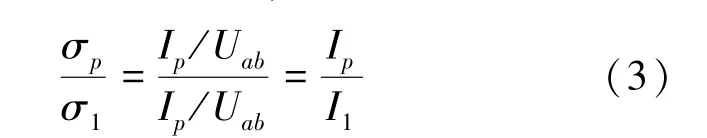
我们知道当点占据概率p＜pc时，没有电流通过该随机电阻网络，即Ip=0，从而相对电导为0；而当p＞pc后，电流Ip≠0，即相对电导不为零。从而我们可以通过电流的有无反映出随机网络的导通情况。在实验中，随着导体球占据概率逐渐减小，电流会从I1减小到0。通过测量Ip/I1随占据概率p的变化，可以估算出正方形格子上点渗流的临界占据概率的值。同时，当随机网络导通时，还可以通过查看格点占据位形图，找到其中的渗流集团和该渗流集团中的骨架结构及关键占据格点。并可通过去除关键占据格点，渗流集团将不复存在，电流也将变为0以展示关键占据格点在渗流集团中重要性。

2　实验装置和位形图

渗流实验仪由均匀打有小孔的有机玻璃板、导体小球、电流表、稳压器和随机数表组成。实验装置图和位形图如图2所示。

图2　渗流实验装置图和位形图

3　实验步骤及数据处理与分析

1）p=1，即将有机玻璃板上的小孔用金属导体球全部填满，调节稳恒变压器的输出电压Uab使得电流表中的读书尽可能接近满量程，记电流表此时读数为I0（实验中典型取值分别为8.5 V，480 mA）。在余下步骤中，保持该输出电压Uab不变。在实验记录纸上记录随机占据概率p=1和对应电流表读书I=I0。

2）使随机占据概率p以最小单位Δp=0.05逐渐降低，利用随机数表不断的随机取出导体小球，余下的占据小球就组成一个随机占据电阻网络。比如p=0.90随机占据的实现方式为查询两位数组成的随机数表，如果两位数读数≥90（因为两位数的随机数的读数范围为［00，99），则该位置对应格点的导体小球将被取出，形成空缺格点。机制实现这些导体和绝缘小球随机地占据有机玻璃上的小孔。完成各格点对应随机数的核对后，在记录纸上记录占据概率p=0.90及其对应的电流表读数Ip=0.90。对该同一张随机数表，取出两位随机数对应读数位于［85，90）之间的格点导体小球，从而实现p=0.85的格点占据，在记录纸上记录相应的占据概率和电流表读数。以此类推，直到在取某占据概率p时，电流表读数为0，记录此时的占据概率和电流值，则完成一次随机格点占据的渗流实验。导致电流表读数为0的那个被取出的占据格点，即为该渗流集团中的关键占据格点。

3）重复实验并做平均，取另外一张随机数表，重复步骤1）和2）并记录相关数据。如我们进行了n张随机数表的实验，则相当于对每一个占据概率，进行了n测量，故占据概率p对应无量纲化后电流平均值为

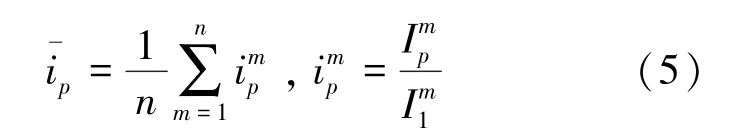
5）实验数据处理与分析。我们在一次大约90分钟的实验课内，让学生测量了4组数据如表1所示。利用公式（5）进行处理，结果绘制图形于图3中。该图与文献［9］中的图2（a）相似，因此可以定性演示渗流相变的存在，并可以估计渗流概率约为0.6。

表1　实验数据记录及处理

4　结 论

通过介绍渗流相变理论和相关实验仪器的研究进展，我们利用打有均匀孔并被铜丝连接相邻的有机板与随机数表，构造可重复使用并可以重复再现实验结果的渗流相变仪器。通过处理和分析在一次实验课的时间内一组学生的实际测量结果，我们可以定性演示渗流相变的存在并估计渗流概率的值，同时还可以呈现渗流集团及其中的关键连接格点等属性，增强学生对渗流相变的理解。

图3　渗流实验结果图。横轴为随机占据概率，纵轴为Ip/I1，即表1中的

［1］ D.Stauffer，A.Aharony.Intorduction to Percolation Theory（2nd）［M］.London:Taylor&Fracis，1991.

［2］ A.Gandolfi.Percolation Methods for SEIR Epidemics on Graphs，in:V.Rao，R.Durvasula（Eds.），Dynamic Models of Infectious Diseases:Non Vector-Borne Diseases，vol.2，New York:Springer，2013，p31-58.

［3］ A.G.Hunt.Percolation Theory for Flow in Porous Media［M］.Heidelberg:Springer，2005.

［4］ Y.Li，D.Y.Wu，X.S.Huang，ed.Percolation of Interacting Classical Dimers on the Square Lattice［J］. Physica A，404:p285-290，2014.

［5］ G.A.Schwartz，S.J.Luduena.An Experimental Method for Studying Two-dimensional Percolation［J］.Am.J. Phys.72（3）:364-366，2004.

［6］ S.E.Gerofsky，M.W.Meisel.Hole-punching Paper for Physics and Fun:a Two-dimensional Percolation Exercise［J］.Physics Education，37（3）:262-263，2002.

［7］ M.Basta，V.Picciarelli，R.Stella.An Introduction to Percolation［J］.Eur.J.Phys.15:97-101，1994.

［8］ R.Mehr，T.Grossman，N.Kristianpoller，ed.Simple Percolation Experiment in Two Dimensions［J］.Am.J. Phys.54（3）:271-273，1986.

［9］ B.J.Last，D.J.Thouless.Percolation Theory and Electrical Conductivity［J］.Phy.Rev.Lett.27（25）:1719-1721，1971.

［10］于渌，郝柏林，陈晓松.边缘奇迹:相变和临界现象［M］.北京:科学出版社，2005:p63-65.

［11］杨展如.量子统计物理学［M］.北京:高等教育出版社，2007:268-276.

Percolation Experiment

LI Yang，ZUO Yin，ZHAO Yu-lian，ZHOU Chang-hong
（Tianjin Agricultural University，Tianjin 300384）

A simple reusable percolation experimental instrument is designed based on the percolation theory. This experiment can be carried out at an undergraduate physics laboratory，or even at a high school laboratory. By measuring currency under different occupied probability，a curve representing the relative conductivity as a function of concentration p，which is averaged over 4 experiments，is presented.This curve has the same result with the reference and demonstrates the existence of percolation phenomena.

percolation；occupied probability；conductivity

O414.2；O4-33

A

10.14139/j.cnki.cn22-1228.2015.02.013

1007-2934（2015）02-0049-04

2014-11-15

天津市科技型中小企业创新基金项目（14zxcxsn03230）；天津农学院青年科技发展基金项目（2012N08）；“渗流演示仪”在第十届高等学校物理演示实验评比中获二等奖