关于三次函数图象切线问题的探讨

韩尚石

（延吉市教师进修学校，吉林　延吉　13000）

关于三次函数图象切线问题的探讨

韩尚石

（延吉市教师进修学校，吉林延吉13000）

近年来，三次函数图象的切线问题在高考中时常出现，一些考生感到束手无策。本文利用高等数学知识，探讨了三次函数过定点的切线问题，以期为学生解决此类问题提供新的方法、新的思路。

三次函数图像；切线问题；高等数学；方法；思路

过一点作三次函数图象切线的问题，在历年高考试题当中频频出现。如2009年江西省文科第12题，2004年天津市理科第20题，2004年重庆市文科第15题等。这类问题对于一些高考考生来说会感到束手无策，不知如何去解决。那么，如何才能顺利解决此类问题，在高考中能迎刃而解呢？本文借助高等数学知识，对三次函数f（x）=ax3+bx3+cx+d （a≠0）图像过定点p（m，n）可作几条切线的问题进行了研究，给出了解决此类问题的方法和思路。

一般地，三次函数f（x）=ax3+bx3+cx+d （a≠0）图像过定点p（m，n）可作几条切线呢？下面给出解决方法：

设三次函数f（x）=ax3+bx3+cx+d （a≠0）上的点（切点）的坐标为M（t，f（t）），则过点M（t，f（t））的三次函数的切线l的斜率为:

k=f´（t）=3at2+2bt+c

所以，切线l的解析式为

y-f（t）=f´（t）（x-t）

由于切线l过点p（m，n），所以n-f（t）=f´（t）（m-t）。

令g（t）=f´（t）（t-m）-f（t）+n，于是切线的条数就是由g（t）在实数集R上零点的个数决定的。

因为g´（t）=f"（t）（t-m），f´（t）=3at2+2bt+c，f"（t）=6at+2b，故g´（t）=（6at+2b）（t-m）。

1.若t1=t2，则g（t）是单调函数，故切线l只有一条；

2.若t1≠t2，则g（t1），g（t2）分别是函数g（t）的两个极值（极大值，极小值），现结合g（t）的图象讨论：

（1）当g（t1）g（t2）＞0时，图象的大致形状是（图1），g（t）有且只有一个零点，故切线l只有一条，说明过点p（m，n）可以作f（x）的一条切线。

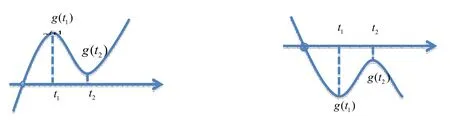
图1

（2）当g（t1）g（t2）=U时，图象的大致形状是（图2），g（t）有且只有两个零点，故切线l只有两条，说明过点p（m，n）可以作f（x）的两条切线。

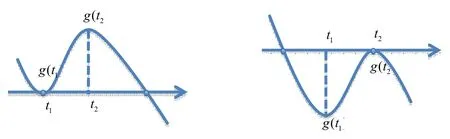
图2

（3）当g（t1）g（t2）＜U时，图象的大致形状是（图3），g（t）有且只有三个零点，故切；线l有三条，说明过点p（m，n）可以作f（x）的三条切线。

图3

所以：

当且仅当g（t1）g（t2）＞U时，三次函数f（x）切线l只有一条；

当且仅当g（t1）g（t2）=U时，三次函数f（x）切线l只有两条；

当且仅当g（t1）g（t2）＜U时，三次函数f（x）切线l有且只有三条。

例题:过点P（1，a）可作f（x）=x3-3x 的三条切线，求a的取值范围。

解：设M（t，f（t））为切点，切线l的斜线为k，则k=f′（t）=3t2-3，

所以l的解析式为

y-（t3-3t）=（3t2-3t）（x-t ））。

由于P（1，a）在切线l上，所以，a-（t3-3t）=（3t2-3t）（1-t ），即2t3-3t2=a-3。

令g（t）=2t3-3t2+3-a ，则切线l的条数与g（t ）在实数集R的零点个数相同。

由于g′（t）=6t2-6t ，令g′（t）=0时，可得出t1=0，t2=1。因为当且仅当g（t1）g（t2）＜0时，切线l有三条，所以（3-a）（2-3+3-a）＜0，即（3-a）（2-a）＜0，得2＜a＜3。

所以，当2＜a＜3时，过点P（1，a）可作f（x）=x3-3x 的三条切线。

以上，我们探讨三次函数图象的切线问题，并给出了判断的方法和解题思路，希望能为学生的进一步学习和探讨提供帮助。

G633.6

A

1673-4564（2015）01-0079-02

2015—01—06