基于非下采样Shearlet变换与压缩感知的图像融合

陈 贞，邢笑雪

（1.莆田学院信息工程学院，福建莆田351100；

2.长春大学电子信息工程学院，吉林长春130022）

基于非下采样Shearlet变换与压缩感知的图像融合

陈 贞1∗，邢笑雪2

（1.莆田学院信息工程学院，福建莆田351100；

2.长春大学电子信息工程学院，吉林长春130022）

针对非下采样剪切波变换（NSST）分解后图像的高频系数数据量较大且具有较大稀疏性的问题，本文提出一种基于NSST和压缩感知（CS）的图像融合算法.算法首先采用NSST对源图像进行分解；其次利用CS算法将NSST分解后的图像的高频系数进行压缩、融合及重构；然后利用“局部区域能量和局部区域方差”联合指导待融合图像的低频系数的融合；最后利用NSST逆变换重构融合图像.由于只需要对高频系数的压缩值进行融合，因此算法可以在不影响图像融合效果的同时加快代码的运行速度.仿真实验表明，该算法不需要原图像的先验知识就可以完成图像的融合，当图像的尺寸较大时，该算法牺牲了微小的融合图像质量，但却可以显著提高算法的运行速度，减小代码的时间代价，降低对硬件系统的要求.该算法对于融合系统的实时性要求提供了一种思路，具有较大的应用价值.

图像融合；非下采样剪切波变换；压缩感知；局部区域能量；局部区域方差

1　引 言

多源图像融合领域，融合算法的时间代价不仅取决于算法的好坏，很大部分还取决于待处理图像的数据量的大小.如何高效地表示和分析图像是图像融合领域的一项核心问题.图像表示方法的有效性直接决定了融合图像的质量.非下采样剪切波变换（NSST）是目前最为先进的一种多尺度多方向的分析方法［1-2］，它在各个方向和各个尺度上对图像实现真正的稀疏表示.基于NSST的图像融合算法能取得较好的融合效果，但是，图像进行多尺度分解后得到的高频系数将随着分解层数和方向数的增加而增加，对这些系数进行处理时将大大加剧硬件和软件的消耗.

压缩感知（Compressed Sensing，CS），也称压缩传感或压缩采样理论，2006年由Candès和Donoho提出［3-4］，其在信号采样的同时完成信息的压缩.将CS应用到图像融合可以减少图像的采样率、存储量和计算复杂度，有效的降低对硬件的要求.因此，近年来，很多学者将目光转向CS域图像融合算法的研究［5］；2009年，Xiaoyan Luo等人在CS的基础上提出了对测量值基于熵的加权平均的融合规则［6］；2010年，Juanjuan Han等对文献［5］中的方法进行了改进，并与文献［6］中的方法进行比较，得到了更为优越的结果［7］；2012年，Guidong Liu提出了基于CS的超声波图像融合算法［8］；2013年，Shutao Li提出了一种基于字典学习的稀疏表示的遥感图像融合算法［9］.

如果能够对图像数据进行压缩感知并进行无失真的重构，即将CS应用到图像融合领域，既对融合的效果没有影响，同时又可以加快算法的执行效率.本文在综合分析了CS的基础上，提出一种基于NSST和CS的图像融合算法.该算法具有以下特点:一方面，NSST可以完成图像的多尺度分解和方向滤波，提取出图像的低频和高频信息；另一方面，针对多个待处理的方向子带，CS可以完成对其的压缩、感知、融合及重构，在较低采样率下得到较好的融合效果.

2　非下采样剪切波变换

当维数n=2时，具有合成膨胀的仿射系统AAB（ψ）形式如下:

其中:y∈L2（R2），A，B是2×2可逆矩阵，|det B|=1.如果A AB（ψ）具有如下形式的Parseval框架（也称紧框架），则这个系统的元素称为合成小波［10，11］，即对任意的f∈L2（R2），有

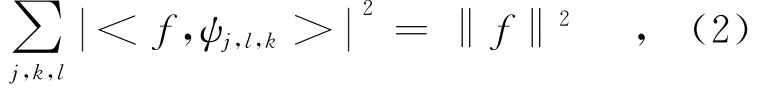
其中，矩阵Aj关联尺度变换，Bl关联几何变换，例如旋转和剪切变换操作等.

为剪切波系统，ψast（x）即为剪切波.

NSST的实现主要分为两个步骤［12，13］:

（1）非下采样的多尺度剖分.非下采样金字塔分解（Non-subsampled Pyramid，NSP）采用二通道非下采样滤波器组使NSST具备了多尺度性，源图像经一层NSP后将会得到图像的低频系数fa1和高频系数fd1，之后每层的NSP分解都在上层分解得到的低频分量上进行迭代以获取图像的奇异点.由于在NSST过程中不存在下采样，因此，图像f经层NSP分解后，最终可得k+1个与f大小相同的子带图像.这k+1个图像包括1个低通图像和k个带通子带图像.

（2）方向局部化.NSST利用剪切波滤波器实现高频图像的方向局部化.具体实现过程为:

1）将伪极化坐标映射到笛卡尔坐标；

2）利用”Meyer”小波构造窗函数，生成剪切波滤波器；

3）将k个带通子带图像和”Meyer”窗函数进行卷积操作，然后获得方向子带图像.

综上所述，在固定分辨率水平j的剪切波变换的框图如图1所示.

图1　NSST的实现流程图Fig.1　Flow chart of NSST

3　压缩感知的基本理论

CS是一种全新的、能够在采样的同时实现压缩的理论模型，CS的压缩、采样过程见图2.压缩感知理论框架主要包括三个重要的内容:（1）信号的稀疏表示；（2）观测矩阵的设计；（3）信号的重构.

图2　CS模型Fig.2　CS model

实现步骤如下:

（1）首先，如果信号X∈RN在某个正交基或紧框架Ψ上是稀疏的或者是可压缩的，求出变换系数Θ=ΨTX，Θ是X的等价或逼近的稀疏表示；

假设一维离散信号X的列向量为X=［X1，X2，…，XN］T，则任意的一组N维向量可以用一个N×1维的向量基｛Ψi｝Ni=1表示，假设这个向量基正交，则通过矩阵Ψ=［Ψ1，Ψ2，…，ΨN］，信号X可以表示成:

其中，θi=＜ΨiT，X＞，Θ和X是N×1维矩阵，Ψ为N×N维矩阵.

（2）其次，设计一个平稳的、与变换基Ψ不相关的M×N维的观测矩阵Φ；

用一个大小为M×N（M＜N）的观测矩阵Φ=｛φ1，φ2，…，φM｝对稀疏信号Θ进行线性投影，计算｛φj｝jM=1与各向量Θ之间的内积，经过M次观测，得到线性观测值yj=＜Θ，φjT＞（j=1，2，…，M），记M×1（M≤N）维的观测集合为Y=（y1，y2，…，yM）.这个过程也可以看做是信号在观测矩阵上从高维向低维投影的过程，则Y满足:

其中:Φ为M×N的矩阵，Y为M×1的矩阵，即矩阵X的观测值.

（3）最后，利用0-范数意义下的优化问题求解X的精确或近似逼近.

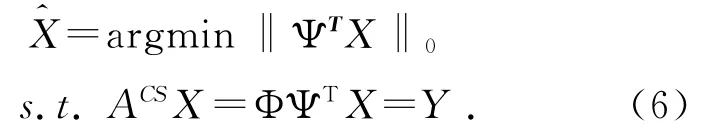
4　基于NSST与CS的图像融合算法

4.1融合框架

利用NSST对待融合图像进行分解后，由于低频系数不具有稀疏性，因此基于NSST和CS的图像融合算法只对高频系数进行CS处理，将低频系数和高频系数分开进行处理可以得到更好的融合效果.图3为NSST和CS相结合的图像融合方法示意图.

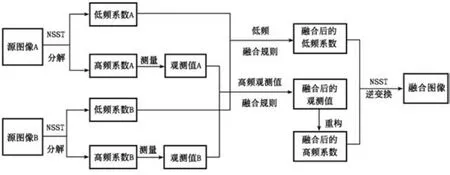
图3　基于NSST和CS的图像融合框架Fig.3　Image fusion frame based on NSST and CS

设待融合图像为A和B，融合后图像为F.基于NSST和CS的图像融合的具体操作步骤如下:

Step 1:将待融合的图像A和B进行配准，本文算法中A和B均已完成配准；

Step 2:对已配准的图像A和B进行NSST分解，得到其子带系数｛AL，AHj，k｝和｛BL，BHj，k｝.其中，AL、BL表示图像的低频系数，AHj，k、BHj，k表示图像在第j层第k个高频子带系数.分解层数设为3层，即j∈｛1，2，3｝，其中，j=1，k=4；j=2，k=4；j=3，k=8；

Step 3:采用“局部区域方差和局部区域能量”联合指导的策略对Step 2中AL和BL加权处理，进而得到FL；

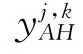
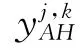
Step 7:对｛FL，FHj，k｝进行NSST逆变换，得到最终的融合图像F.

4.2低频系数的融合规则

低频系数代表轮廓信息，图像的低频分量集中了图像的主要能量，反映图像的近似和平均特性，是源图像的逼近，不具有稀疏特点，因此不能采用CS对其进行处理.局部区域方差表明了该区域灰度变化的剧烈程度，在一定程度上也反映了该区域图像的清晰程度.为此，本文将局部区域能量和局部区域方差结合对待融合图像的低频系数进行融合.

图像A和图像B的低频系数AL（r，c）和BL（r，c）的局部区域方差为VA（r，c）和VB（r，c），区域能量EA（r，c）和EB（r，c），计算公式如式（7）～式（9）所示.

其中:Ω（r，c）为以像素点（r，c）为中心的m×n大小的邻域窗口，一般为3×3或5×5，本文中选取3×3的邻域窗口.fPL（m，n）为图像PL在（m，n）处的像素值，w（m，n）为（m，n）处对应的窗函数，EPL（r，c）为像素（r，c）的局部能量.

融合图像F的低频系数FL（r，c）采用加权平均算子来进行融合，计算公式如式（10）所示.

其中:ωA（r，c）和ωB（r，c）满足式（11）.

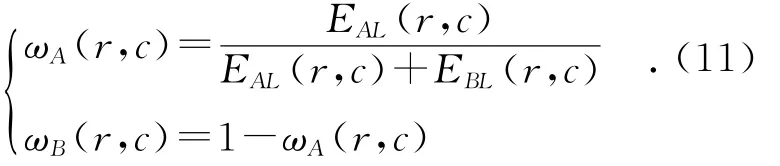
4.3高频系数的融合规则

由于图像的高频系数反映的是图像的细节信息，如直线、曲线、边缘、纹理等信息，系数的绝对值越大，表示该处亮度变化越剧烈，因此在进行图像融合时，应尽量选择源图像中清晰的部分来获得融合系数.NSST分解得到的高频波段的系数大部分在零值左右波动，只有小部分的高频系数具有较大的幅值，所以依据CS理论，可以认为高频系数具有较大的稀疏性.为此，本文选用CS算法对稀疏度较大的高频系数进行压缩，这样可以加快算法运行速度，降低时间损耗.

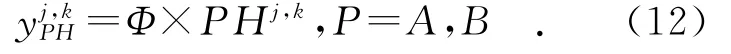
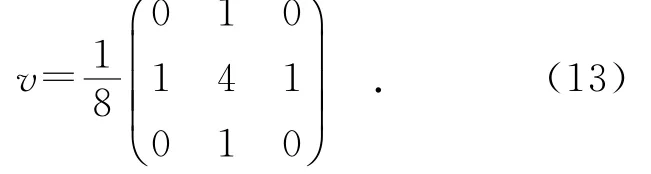
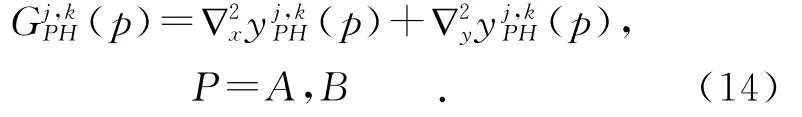
其中，R是n×m的一个矩形区域，nR=n×m，一般为3×3或5×5，本文中选取3×3的邻域窗口.j=1，2，3，…代表分解尺度，k=｛k1，k2，…，kj｝表示在每一个分解层上对应的方向个数.

5　仿真实验和结果分析

为了验证本文提出的基于NSST和CS的融合算法的有效性和正确性，本文选用红外与可见光图像图4所示、多聚焦图像图6所示和医学图像图8所示来进行仿真实验.实验平台为Matlab2011（a），计算机主机配置为:Intel（R）处理器，CPU主频3.4 GHz，内存8 GB.实验对比了本文提出的算法和其他4种算法在相同的融合规则下的时间代价及融合效果.其他4种算法分别为:算法（1）:基于NSST的图像融合算法；算法（2）:基于CS的图像融合算法；算法（3）:文献［14］中的基于DWT和CS的图像融合算法［14］；算法（4）:文献［15］中的基于NSCT和CS的图像融合算法［15］.

由于不同的采样率M/N下图像的重构效果不同，采样率M/N越高，图像的重构效果越好，但是需要的重构时间越长.本文对不同采样率M/N下（M/N设置为0.1～1，M以5递增）的6幅实验图像的PSNR、MI、CORR和重构时间T进行了对比，当采样率M/N为0.3时，在不太影响图像的重构效果的同时所需的重构时间也较小.因此，在本文中，CS算法中的采样率均选择为0.3.

图4　“Bristol Queen's Road”源图像Fig.4　Source images of Bristol Queen's Road

参数设置方面，算法（1）中，NSST设置为3层尺度分解，剪切方向数为｛4，8，8｝；算法（2）中，CS采用小波稀疏基进行稀疏，高斯随机矩阵进行观测，OMP算法进行重构，M/N设置为0.3；算法（3）中，小波分解层设定为3层，采用“sym8”小波函数，CS的参数设定与本文算法（2）一致；算法（4）中，NSCT分解层数设为3层，尺度分解滤波器采用“maxflat”滤波器，方向分解滤波器选用“dmaxflat”滤波器，CS的参数设定与算法（2）一致；算法（5）即本文算法中，NSST设置与算法（1）一致，CS参数设定与算法（2）一致.

对于所有的算法，融合规则均采用本文提出的融合方法.实验选用熵值（E）、平均梯度（AG）、标准差（SD）、边缘信息保留量（QAB/F）、空间频率（SF）和算法耗时（T）6个参数来综合评价各种方法融合图像的质量.

（1）红外和可见光源图像

图5　“Bristol Queen's Road”源图像融合结果Fig.5　Fusion results of source images of Bristol Queen's Road

从图5可以看出，5种算法均可以实现“Bristol Queen's Road”图像的融合.从视觉效果来看，NSST算法可以得到最好的视觉效果，道路的边缘、广告牌上的细节信息均得到了很好的体现；CS算法得到的视觉效果是最差的，分析其原因主要是因为实际图像的稀疏性较差导致重构效果较差；NSST+CS算法中首先对图像进行NSST分解，只对其稀疏的高频系数进行观测重构，其融合效果仅次于NSST算法且优于DWT+CS和NSCT+CS.从客观参数上来看，NSST+CS算法的耗时T是所有算法中耗时最低的，其SD、E、AG、QAB/F和SF仅小于NSST，但高于CS算法、DWT+CS算法和NSCT+CS算法.

（2）多聚焦源图像

对图6和图7的融合结果进行分析，可以发现NSST+CS算法可以将多聚焦图像进行较好的融合，源图像的边缘和细节信息可以被较好的传递到融合图像中去.对表1分析表明，NSST+ CS算法得到的客观参数值较大，且算法的时间消耗最小.主观效果评价和客观参数度量均论证了NSST+CS算法是一种切实可行的融合算法.

图6　“Pepsi”多聚焦源图像Fig.6　Multi-focus source images of Pepsi

图7　“Pepsi”多聚焦源图像融合结果Fig.7　Fusion results of Multi-focus source images of Pepsi

图8　“脑血管”源图像Fig.8　Source images of Cerebrovascular

（3）医学源图像

图8和图9的融合结果表明，NSST+CS的融合效果弱于NSST，主要是因为CS对高频系数进行了70%的压缩，这就导致在重构时图像的边缘和细节信息没有NSST算法那么丰富；同时，由于NSST+CS算法采用了NSST多尺度分解工具，图像的细节和边缘可以被很好的提取，因此其融合效果要优于DWT+CS和NSCT+CS的算法.从表1可以看出，由于医学图像的稀疏性较好，所以采用NSST+CS进行图像融合时，不仅可以得到较大的客观参数值，并且算法运行的时间较快，可以较好的满足硬件系统的实时性的要求.

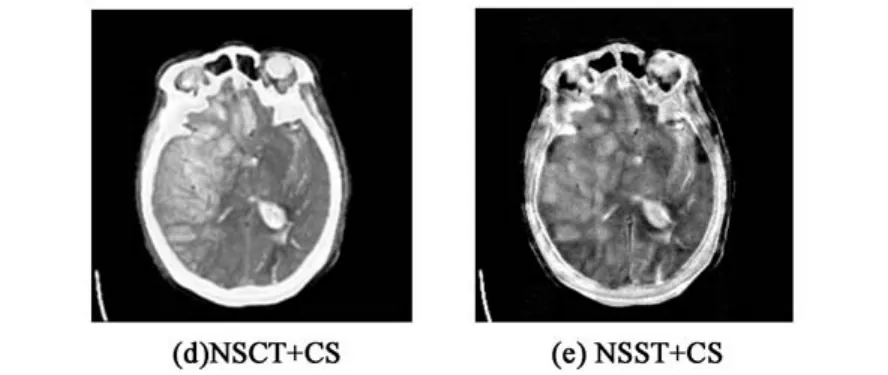
图9　“脑血管”源图像融合结果Fig.9　Fusion results of source images of Cerebrovascular

6　结 论

针对NSST分解后图像的高频系数数据量较大且具有较大稀疏性的问题，本文提出一种基于NSST和CS的图像融合算法.算法的核心思想是首先采用NSST对源图像进行分解；其次利用CS算法将NSST分解后的图像的高频子带系数进行压缩、融合及重构，其中，高频观测值的融合采用“局部区域能量和全局梯度”联合指导的策略；然后利用“局部区域能量和局部区域方差”联合指导低频分量的融合；最后利用NSST逆变换重构融合图像.

由于只需要对高频系数的压缩值进行融合，因此算法可以在不影响图像的融合效果时又可以加快代码的运行速度.本文分别使用红外及可见光图像、医学图像和多聚焦图像对算法进行了验证，仿真实验表明，该算法不需要原图像的先验知识就可以完成图像的融合，当图像的尺寸较大时，该算法虽然牺牲了融合图像质量，但是却可以显著提高算法的运行速度，减小代码的时间代价，降低对硬件系统的要求.该算法对于融合系统的实时性要求提供了一种思路，具有较大的应用价值.

［1］ Guo K，Labate D，Lim W Q.et al.Wavelets with composite dilations and their MRA properties［J］.Applied and Computational Harmonic Analysis，2006，20（2）:202-236.

［2］ Lim W Q.The discrets shearlet transform:A new directional image representation and compactly supported shearlet frames［J］.IEEE Transactions on Image Processing，2010，19（5）:1166-1180.

［3］ Candès E J.Compressive Sampling［C］.Proceedings of the International Congress of Mathematicians，Madrid，Spain:European Mathematical Society，2006.

［4］ Donoho D L.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52（4）:1280-1306.

［5］ Wan T，Canagarajah N，Achim A.Compressive image fusion［C］.15th IEEE International Conference on Image Processing，San Diego，CA:IEEE，2008:1308-1311.

［6］ Luo X Y，Zhang J，Yang J Y，et al.Image fusion in compressed sensing［C］.2009 16th IEEE International Conference on Image Processing，Cairo:IEEE，2009:2205-2208.

［7］ Han J J，Loffeld O，Hartmann K，et al.Multi image fusion based on compressive sensing［C］.2010 International Conference on Audio Language and Image Processing，Shanghai:IEEE，2010:1463-1469.

［8］ Liu G D，Shen Y.Ultrasonic image fusion using compressed sensing［J］.Electronics Letters，2012，48（19）:1182.

［9］ Li S T，Yin H T，Fang L Y.Remote sensing image fusion via sparse representations over learned dictionaries［J］. IEEE Transactions on Geosciences and Remote Sensing，2013，51（9）:4779-4789.

［10］ Easley G，Labate D，Lim W Q.Sparse directional image representations using the discrete shearlet transform［J］. Applied and Computational Harmonic Analysis，2008，25（1）:25-46.

［11］ Guo K H，Labate D.Optimally sparse multidimensional representation using shearlets［J］.SIAM J.Math. Anal.，2007，39（1）:298-318.

［12］ 王雷，李彬，田联房.基于平移不变剪切波变换的医学图像融合［J］.华南理工大学学报（自然科学版），2011，39（12）:13-19.

Wang L，Li B，Tian L F.Medical image fusion based on shift-invariant shearlet transformation［J］.Journal of South China University of Technology（Natural Science Edition），2011，39（12）:13-19.（in Chinese）

［13］ 高印寒，陈广秋，刘妍妍.基于图像质量评价参数的非下采样剪切波域自适应图像融合［J］.吉林大学学报（工学版），2014，44（1）:225-234.

Gao Y H，Chen G Q，Liu Y Y.Adaptive image fusion based on image quality assessment parameter in NSST system［J］.Journal of Jilin University（Engineering and Technology Edition），2014，44（1）:225-234.（in Chinese）

［14］ 杨粤涛.基于非采样Contourlet变换的图像融合［D］.长春:中国科学院长春光学精密机械与物理研究所，2012.

Yang Y T.Research on image fusion based on nonsubsamepled Contourlet transform［D］.Changchun:Changchun Institute of Optic，Fine Mechanics and Physics of Chinese Academy of Science，2012.（in Chinese）

［15］ 沈瑜.一种改进小波变换的图像融合方法［J］.自动化与仪器仪表，2013（5）:202-204.

Shen Y.An improved wavelet transform image fusion algorthm［J］.Automation&Instrumentation，2013（5）: 202-204.（in Chinese）

Image fusion algorithm based on non-subsampled Shearlet transform and compressed sensing

CHEN Zhen1∗，XING Xiao-xue2

（1.Information Engineering Department，Putian University，Putian 351100，China；
2.College of Information Engineering，Changchun University，Changchun 130022，China）

After the image decomposition with NSST，the high-frequency coefficients have a large amount of data and greater sparsity.In order to obtain fusion results rapidly，an image fusion algorithm based on Non-subsampled Shearlet Transform（NSST）combined with Compressed Sensing（CS）is presented.Firstly，the source images are decomposed with NSST；secondly，the high-frequency sub-band coefficients of the decomposed images are compressed，fused and reconstructed by CS；then，based on local area variance and local area energy，the low-frequency coefficients was fused；finally，the inverse NSST is used to get the final fused image.Because only the compressed values of the high frequency coefficients are fused，the image fusion effects can't be affected，and the running time of the algorithm can be reduced.In this paper，the multi-focus image，medical image and infrared andvisible images are used to verify the effectiveness of the algorithm.The simulation results indicate that this algorithm can achieve the fusion of the image without prior knowledge of the original image. When the image size is larger，although the fusion image quality is sacrificed，it can significantly improve the speed to reduce the time cost and hardware requirements.The algorithm provides an idea on how to satisfy the real time requirements in the fusion system，which has a great practical value.

image fusion；non-subsampled Shearlet transform；compressed sensing；local area variance；local area energy

TP391.41

A doi:10.3788/YJYXS20153006.1024

1007-2780（2015）06-1024-08

陈贞（1977-），女，福建莆田人，硕士，讲师，主要从事图像处理、粗糙集理论方面的研究.E-mail:chenfjpt@ yeah.net

邢笑雪（1981-），女，山西霍州人，博士，讲师，研究方向为数字图像处理、模式识别等.

2015-01-05；

2015-02-05.

国家教育部“春晖计划”项目（No.Z2014138）；吉林省教育厅基金项目（No.20140529）；莆田市科技计划项目（No.2014G20）

Supported by Chunhui Project of the National Education Department，P.R.（No.Z2014138）；Education Department Foundation of Jilin Province（No.20140529）；Science and Technology Plan of Putian City（No.2014G20）

∗通信联系人，E-mail:chenfjpt@yeah.net