数学证明思维模型的建构与应用

数学证明思维模型的建立，表明了数学证明思维活动的实质性内涵与组成环节，从而为数学证明的教学设计提供了一套可以参考的程序，增加教学的有效性。利用数学证明的教育资源可以培养学生运用证据说话的能力，这是生活在民主社会中的人必备的素质;可以促进学生将适应生存的“短时间的思考”转化为实现自我、实现目的所需要思维基础“长时间的思考”的能力，为发挥学生的智力潜能提供了现实性。

数学证明模型  数学教学设计  长时间的思考

一、数学证明的内涵与方式

关于“证明”的释义，《现代汉语词典》将其界定为“用可靠的材料来表明或断定人或事的真实性”。由此，我们可以将数学证明刻画为：从真理性的数学知识出发、运用演绎推理的形式说服别人接受从命题的题设条件过渡到题断结论的真实性的一种信念。演绎推理的形式只有在数学领域内，才被认为是唯一有效的证明方式;其他情况下，证明过程大部分是以个人经验和接受权威的证实为基础的。数学证明过程，是经过主体的思维活动，选择合适的真理性的数学知识，把作为外在信息的题设条件中的杂乱无章的元素，通过演绎推理，组织成为具有因果关系序列结构的题断结论要求的过程。

外在于主体的客体信息，是由人类心理已经具有的观念（源于真理性的知识或曾经经历过的活动经验等，提供给主体处理面临新信息时的活动意向或指令）而赋予了外在信息以知识结构的意义，否则，客体就是无意义的“物自体”[1]。而这种赋予外在信息以意义的过程就是一系列的合情推理的心理活动过程，将这些合情推理的真实性结论转化为条分缕析的演绎推理及其表达的过程就构成了数学证明。

二、数学证明思维模型建构

在发生数学证明的思维活动中，发现证明思路的信息元素序列结构的本质，势必通过设法使题设条件元素组成正确率比较高的信息脉络轮廓（与知识框架相比较）——元素序列结构的雏形，借此信息脉络轮廓的中介才能选择出成功性比较高的数学知识（定义、公理或定理）组织信息，从而决定选择与利用数学知识作为封装信息的结构框架（其实是知识结构框架与信息轮廓的互相吸引与适应的过程），生成有价值的信息结构（类似于主体所选用的数学知识结构）。

本研究试图建立证明的思维模式，这一过程可以概略地叙述为：首先，主体从题设条件信息元素中选择并确定出“支点信息”，选择“支点信息”的心理活动又是由外在信息与已经内化并保存在意识中的数学知识结构之间的互相吸引、相互诱导、相互调整而获得的;其次，基于“支点信息”，并在“支点信息”这一“凝聚核”的作用下，使外在诸多的外围信息元素组织成一种脉络轮廓;最后，由这种信息轮廓提示主体选择数学知识框架来封装题设条件的信息元素，获得某种结构，从而赋予题设条件信息以某种知识结构的意义（如图1所示[2]）。

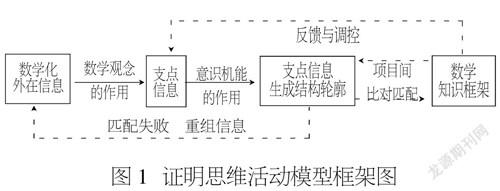
从这一模型中可以看出，在分析题设条件信息元素伊始，主体不可能迅速确定地把握信息元素所能组成具有结论意义上的结构，就势必动用自己的知识库中的知识框架猜想信息元素可能具有某种结构。依据信息的某个侧面（“支点信息”）赋予“支点信息”决定的知识结构，再将信息元素组织成具有知识结构的意义，如果不成功，就会更换“支点信息”，再做一轮循环。在这一系列思维活动环节中，一定离不开猜想（即合情推理）的作用。因此，证明的思维活动过程环节就是不断地生成猜想（合情推理）与检验猜想、证实或证否猜想，证实了就可以转化为演绎推理，形成证明过程，证否就要更换“支点信息”，再生信息轮廓的又一轮循环。

三、例示数学证明思维模式在教学设计中的应用

教师产生合适的教学行为，并非完全从现代教育理念中演绎来的，而是重在观照现代教育理论，分析具体的知识性质特点，分析学生发生具体知识的心理活动的特点中获得的;从反思与分析自己的课堂教学行为的实践中获得的[3]。证明模式的建立为数学证明教学设计时教师优化分析活动的教学行为提供了方向。

数学教学行为构成要素的基础主要体现在互相关联的三个侧面：对要传授的数学知识点的结构所呈现的环节及其连接中介组成序列的理解（“教材分析”），对学生萌发数学知识（环节及其连接中介）的心理环节（呈现的是观念形态）及其过渡性中介的把握（“学情分析”），通过创造性工作找到这二者之间的联系（“关联分析”）。由此设计出合适的教学过程，使知识的环节及其连接中介适应于学生发生知识的心理活动环节（观念形态）及其过渡性中介的辨证运动过程。下面的框架图（图2[4]）是数学教学设计的一般分析模型。

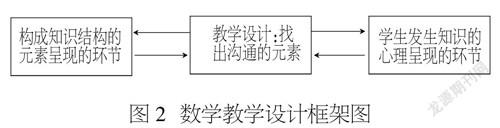
图2  数学教学设计框架图

要发挥证明的思维模型的教育价值，就要教师在第三项“关联分析”上做足功夫，而“关联分析”效果如何取决于“学情分析”与“教材分析”的效果，因此，“三项分析”构成了证明教学设计的基础。数学证明思维活动的“关联分析”过程主要在于认真研究学生选择“支点信息”，确定知识框架，由知识框架把外围信息组织成有序的逻辑环节序列，从而，贯通从题设条件到题断结论的过程。学生正是在教师的引导下，经由这种过程将学生的“短时间的思考”方式转化为“长时间的思考”方式，发展一系列的思维品质。证明思维模式建构，为教学设计“三项分析”活动的展开提供了可以参考的程序序列。

例题：已知，如图3，在矩形ABCD中，从点A向对角线BD作垂线，P为垂足，从点P向BC，CD分别作垂线，垂足分别为E、F。求证：

①

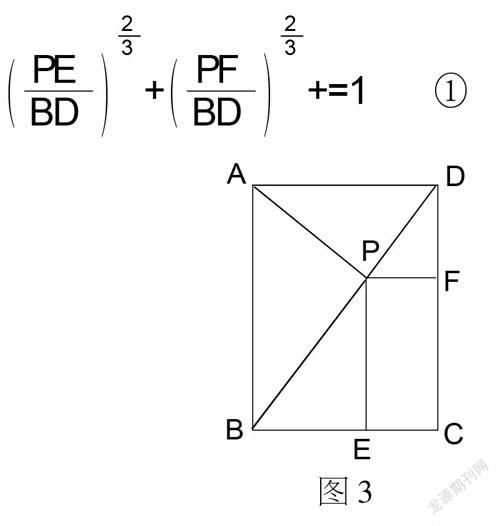
图3

教材分析：由数学证明思维模式可知，证明过程就是运用已经掌握了的数学知识框架将题设条件组织成题断结论的过程。如何选择知识框架构成探究证明思路可否实现的关键环节，它取决于“支点信息”的选择，本例的“支点信息”应该是什么？由于题设条件是如图3的一个图形，线条多，组成了庞杂的系统，难于从题设条件中确定“支点信息”。于是，我们转而从结论式①出发，即将结论式①作为“支点信息”来进行试探，那么，它所决定的知识框架该是什么？通过联想，检索我们已经掌握的数学知识，由sin2？琢+cos2？琢=1②的形式与等式①的形式具有相似性，可以将其确定为封装题设条件信息的知识框架加以试探。下面，我们只需检验，由题设条件的相关信息的设定，从等式①可以过渡到等式②就可以了。

学情分析：“教材分析”由证明思维模式出发，可以找到一条从题设到题断的可能通路，这条思路确保教师可以顺利地利用一种办法解决这道题。但是，教师的想法与论证能否转化为学生发生证明思路的有序的心理活动过程呢？这就需要教师进行“学情分析”，即从学生心理活动的角度来考察证明思路发生的可能性，从而在教学中进行层层铺垫，启导学生自己发现证明思路。发生这条思路具有两个方面的疑难：其一，由“支点信息”①决定知识框架②的选择，这是学生思维活动的疑难;其二，实现从“支点信息”①决定知识框架②的学生思维活动的可能性，这是学生获得技术性手段的疑难，即技能技巧的疑难。两项疑难对于一般学生来说，都必须要经过“长时间的思考”才能解决，正因如此，数学证明可以严格地训练学生的数学思维，优化多方面思维品质。

关联分析：从“教材分析”与“学情分析”所得到了的结论中找出沟通这两项分析所得到结论的元素，进行教学设计。下面是笔者证明这道题的真实课堂教学过程实录（其中，省略号表示学生思维的中断处）。

师：题设条件中具有几个直角三角形，并且这些直角三角形都相似，因此，可以得到许多比例式，也可以得到许多相等的角，但是，并不能明确地知道我们可以选择与组合哪些条件，从而可以过渡到结论式①。怎么办？（注：提示学生选择“支点信息”）

生1：我们可以从结论式①反过来求索条件（注：学生确定了“支点信息”），即用分析法试探，……

师：一个很好的想法，如何试探？

生2：将结论①转化为一个已知的数学公式：sin2？琢+cos2？琢=1②（注：从“支点信息”确定知识框架，解决了确定知识框架的疑难），再从已知条件出发，获得公式②，……

师：又是一个很好的想法，如何从题设条件出发，构造公式②？

生3：我们假设

师：③、④成立吗？怎么办？

生4：重点研究等式③，由于③左边是两个线段之比，右边是一个数的三次方，两边的指数不和谐一致，于是，考虑将左边也变成一个数的三次方的形式，首先把左边变成三个数积的形式：……

师：生4提出了非常合理的想法，可以从图3中选择出线段x，y，从而得到等式⑥吗？

生5：我想这样选择线段x，y：在Rt△ABP中，知等式⑦显然成立（注：解决了从题设条件信息到知识框架途径的疑难），从而等式③成立，同理，等式④成立，于是，等式①成立。

这种教学设计的过程，旨在通过启发法，促进学生自己探究问题解决的思路活动，学生的数学知识不是经过直接授受、机械记忆的方式发生的，教师通过自己的探究活动，将数学知识融入主观意向的因素，进而由这种意向的作用产生相应的“数学观念”，形成相应的假设，教学过程中，教师应想方设法使这些数学观念在教师与学生之间、在主观与客观之间相交相融，甚至移植。教师将探究数学结构认识所生成的情感中裹夹着的“数学观念”先在地移入学生的思维框架中。使学生在发生某特定的数学知识以前，他们的思维结构中先在地建立奥苏贝尔意义上的“锚基”，或维果斯基意义上的“最近发展区”，使学生数学知识发生找到相应的凭依。

从这个例子中可以看出，这些理念的实现，需要教师的三项分析能力。证明思维模式提供教师“教材分析”与“学情分析”的心理意向，由于证明的过程就是寻找知识框架封装题设信息、形成题设信息元素的序列、构成逻辑因果关系的过程，而知识框架的选择取决于“支点信息”的确定。这个思维模型对这两点揭露无疑，为教师的“三项分析”提供了非常明确的程序，从而为教师的有效教学设计奠定了基础。这是它提供了教学设计的价值所在。

数学证明思维模型的建立，使我们发现了数学证明思维活动的实质性内涵与组成环节，从而为教师关于数学证明的教学设计提供了一套可以参考的程序，增加教学设计的有效性。利用数学证明的教育资源可以培养学生运用证据说话的能力，这是生活在民主社会中的人必备的素质;可以促进学生将适应生存的“短时间的思考”转化为实现自我实现目的所需要思维基础“长时间的思考”的能力，为发挥学生的智力潜能作出贡献。

——————

参考文献

[1] [德]康德.纯粹理性批判[M].蓝公武，译.北京：商务印书馆，2012.

[2] 张昆.渗透数学观念的教学设计方法研究：以一元一次方法教学为例[D].重庆：西南大学，2011.

[3] 张昆，曹一鸣.完善数学教师教学行为的实现途径[J].数学教育学报，2015（1）.

[4] 张昆.数学教学设计的新视角——适应学生认识方式的研究[J].教学与管理，2015（4）.

[作者：张昆（1965-），男，安徽合肥人，淮北师范大学数学科学学院中学高级教师，博士。]

【责任编辑  郭振玲】