基于特征线法的畦灌施肥地表水流溶质运移模型研究

李志新 许迪 李益农

摘要 为实现畦灌施肥技术参数的优化组合，建立合理的模型工具至关重要。基于零惯性量模型和一维对流弥散方程ADE作为畦灌施肥水流和溶质运移方程，分别利用有限差和特征线法进行求解，建立基于特征线法的畦灌施肥地表水流溶质运移模型。以隐式有限差解法为对照，对特征线法引入的数值误差状况进行评价。结果表明，相对于隐式有限差解法，采取特征线法求解ADE时引入的数值震荡和数值弥散有显著减少，基于特征线法的畦灌施肥地表水流溶质运移模型更合理。

关键词 畦灌施肥；地表水流；溶质运移；对流-弥散；数值误差

中图分类号 S275.3；S153.5 文献标识码 A 文章编号 0517-6611（2015）05-084-04

Study on Model of Overland Water Flow and Solute Transport to Border Strip Fertigation Based on Characteristic Curve Method

LI Zhixing1， XU Di2， LI Yinong2

（1. School of Civil Engineering， Guizhou Institute of Technology， Guiyang， Guizhou 550003； 2. National Center of Efficient Irrigation Engineering and Technology Research， China Institute of Water Resources and Hydropower Research， Beijing 100044）

Abstract In order to realize the optimized combination of technical factors of border strip fertigation， it is necessary to establish a reasonable model tool. Based on zeroinertia model as flow equation solved by finite difference method， and 1D ADE as solute transport equation solved by characteristic curve method， a overland flow and solute transport model was established based on characteristic curve method. With finite difference method as contrast method， the numerical errors introduced by characteristic curve method were evaluated. The results suggested that when compared with finite method， the numerical errors introduced by characteristic curve method is obviously smaller， and the model of overland flow and solute transport based on the numerical errors introduced by characteristic curve method should be more reasonable.

Key words Border strip fertigation； Overland water flow； Solute transport； Advectiondiffusion； Numerical errors

基金項目 国家863计划重点项目课题（2006AA100210）；国家科技支撑计划重点项目课题（2006BAD11B02）。

作者简介 李志新（1976- ），男，江西抚州人，博士研究生，研究方向：地面灌溉技术。

收稿日期 20141223

畦灌施肥是地面灌溉施肥的一种，预先将化肥充分溶解，并与灌溉水流，混合实施液体施撒的新型施肥方式[1-2]。与地面灌溉的传统氮素化肥施用方式相比，这种施肥方式具有减少能耗、劳动力及其对土壤或作物的扰动破坏等优点[3]，在国外已得到越来越多的推广应用[1-2]，在我国尚处于起步阶段。但是，若缺乏合理的技术管理措施，该方法在施肥均匀性方面的效果不理想，还会产生肥料在土壤深层渗漏的问题[4]。因此，畦灌施肥研究通过探讨施肥时机、入地流量、土壤入渗性能、微地形、坡度等重要技术要素对土壤水氮时空分布的影响[5]，为畦灌施肥系统优化设计管理提供指导。畦灌施肥技术要素及其组合范围较宽泛。对技术要素组合方案进行计算、评价，需要通过数十或数百次的灌溉施肥模拟在较短时间内实现。因此，合理的模型是畦灌施肥系统中优化管理的理想工具。

Abassi等[6]在对地面灌施肥进行模拟研究中，以圣维南方程和一维对流弥散方程ADE作为模型水流和溶质运移控制方程，分别采用有限体积法和CrankNicolson格式隐式有限差进行求解，通过降低网格皮克里特数（Pe）克服对流项离散带来的数值震荡和弥散问题。结果表明，弥散度和输入溶质的浓度对灌溉施肥均匀性的影响较小。值得指出的是，上述研究中在处理ADE中对流项离散带来的数值震荡和弥散问题时，采取降低Pe的方法，对于时空网格剖分有严格限制性要求，而实际中的研究对象时空网格剖分细化程度相当有限[7]。特征线法利用有限差求解ADE中弥散项，而利用质点追踪Lagrange法求解ADE中对流项，最后将两者组合起来，能够有效地解决数值误差问题，而在网格剖分上没有限制[7-8]。

笔者以零惯性量模型和一维ADE作为畦灌施肥水流和溶质运移方程，分别利用有限差和特征线法进行求解，建立畦灌施肥地表水流溶质运移模型，并将特征线法与作为对照的隐式有限差解法引入的数值误差状况进行对比分析，以评价基于特征线法的畦灌施肥地表水流溶质运移模型的性能和合理性。

1 地表水流运动模型

1.1 控制方程及初始和边界条件 采用的零惯性量模型是由完全水动力模型忽略加速度项简化而来的[9]。

qt+qx+I=0

hx=SL-Sf

Sf=q2C2R3

C=1nR1/6（1）

式中，q为入畦水流在任一时刻的断面单宽流量，m3/（min·m）；I为单位长度的入渗率，m3/（min·m）；SL为畦田纵坡；Sf为阻力坡降；h为任意时刻的田面入流水深，m；n为曼宁糙率；t为时间坐标，min；x为距离坐标，m；R为水力半径，m。

初始条件：

h=0，q=0 （t=0）（2）

左边界条件：

q=q0 （0

q=0 （t1

h=0，hx=0（t2

右边界条件：

h=0 （0

q=0 （t3

式中，t1为畦口停水时间，min ；t2为畦口退水时间，min；t3为水流前锋到达畦尾时间，min；t4为退水时间，min；xL为畦长，m；xa为水流前进锋面到达位置，m；其他符号意义同前。

1.2 求解方法 對零惯性量模型采用有限差数值求解[10]。首先，构造其差分格式，单元格划分在时间t轴上采用等步长，在空间x轴上采用不等步长，其值为第k时段δt内水流推进距离δxk，按此构造的单元为一四边形单元，相应的差分方程为非线性方程组，可采用泰勒展开式线性化进行迭代求解（即牛顿迭代法）。求解参数有各结点水深、流量。

由基本模型的边界条件可知，第一时段的水流推进距离与畦首水深不能用基本方程求解，因此根据初始条件与能量方程，建立如下方程组来计算。

q0t-δx1（h01+β+z01+α）=0（8）

βh0δx1+s0=n2q20h10/30（9）

式中，δx1为σt时刻的水流前锋位置，m；β、α分别为反映地表水形状的幂函数关系的指数和Kostiakov入渗公式中的指数（无量纲）；h0为畦首水深，m；其他符号意义同前。该式也是一非线性方程组，可采用牛顿迭代法求解。

2 地表溶质运移模型

2.1 控制方程及初始和边界条件 对于条形畦田，畦田水流中溶质运移可用一维ADE方程[11]来描述。

（hC）t+（qC）x+Ci=x（hDxCx）（10）

式中，h为水深，m；C为溶质浓度，g/m3；t为时间，min；q为单宽流量，m3/（min·m）；x为纵向距离，m；i为入渗速率，m3/（min·m）；Dx为纵向弥散系数，m2/s。

初始条件：在计算区域内，给定初始溶质浓度分布，即

C（x，t0）=0 （x ∈[0 L]，t0=0）（11）

式中，x为畦长，m；t0为初始时刻，min；L为畦田总长，m；其他含义同前。

边界条件：分别为给定浓度和给定通量的边界条件，即

C（x0，t）=C0 （x0=0，t∈[0 T]）（12）

x（hDxCx）-（（qC）x+Ci）|x=L=qL（x=L，t∈[0 T]）（13）

式中，C0为畦首给定边界浓度条件，g/m3；qL为畦尾给定溶质通量边界条件，m3/（min·m）；其他含义同前。

2.2 求解方法

2.2.1 特征线法。对式（9）数值求解采用特征线法[7]。特征线法求解思路的特点是将溶质在水流中的对流和弥散分开，分别加以求解，然后叠加起来。溶质在水流中的运动可视为沿着水流方向以水流速度（u）运动的动坐标系中的纯弥散问题。由于对流作用，运动质点携带初始浓度在一个时步（Δt）内运动了Δl=uΔt的距离，同时由于弥散作用，质点浓度改变了Δc，在Δl位置的溶质浓度为c=c0+Δc。该浓度又被视为下一个时步的初始浓度，还利用弥散作用结果对运动质点浓度进行修正。然后，可以转入下一个时步的质点运动，并计算出该时步末各位置的溶质浓度。

求解具体步骤。首先，剖分研究域成等大小的网格，并放置一定数量的质点，质点的初始浓度由初始条件确定。对于时间步（Δtk+1），每个质点在水流的作用下都沿着速度方向运动一段距离，新的位置通过对下式的差分。

ux=dxdt（14）

得到新位置为：

xk+1p=xkp+Δxp=xkp+uxΔtk+1（15）

p=1，2，L，Np；k=0，1，2，L，Nt-1（16）

式中，xk+1p、xkp分别为质点p在k和k+1时间步的坐标位置；Np为质点总数；Nt为时间步数。

由于质点运动，网格中的质点及其浓度将发生变化。对于i 网格，由对流作用在k+1时间步流入此网格的各质点的浓度平均为Ck+1*i，j。

在确定对流作用引起的浓度改变后，考虑弥散作用、源汇作用等对浓度改变的贡献，可由下式特征线微分方程确定。

dCdt=1nbxi（nbDijCxj）+F（17）

通过对以上方程的差分，可得到弥散作用和源汇作用等所引起的浓度改变。

ΔCk+1i，j=（ΔCk+1i，j）1+（ΔCk+1i，j）2（18）

因此，在得到对流引起的浓度改变Ck+1*i，j和弥散作用、源汇作用等所引起的浓度增量ΔCk+1i，j后，可得到对流弥散方程的解。

Ck+1i，j=Ck+1*i，j+ΔCk+1i，j（19）

2.2.2 对照的隐式有限差解法。作为对照的隐式有限差解法主要包括空间域离散、空间一阶和二阶导数的差分、时间域离散、边界条件施用、差分方程组求解等步骤[6-7]。首先，将一维线形研究域剖分成网格，即差分网格，网格线交点称为格点，网眼称为网格，计算点称为节点。差分法则以网格中央作为计算节点建立差分方程；在此基础上，微分方程式（9）中的一阶、二阶导数用中央差分形式来表示；通过时间域离散，将时间域进行等分，每個部分称为时间步或简称时步，用k来计数，每个部分的长度称为时间步长；时间域离散之后，求t时刻数值解的基本思想是用本时间步k的已知值Ck来计算下一个时间步k+1的浓度Ck+1，使用第j个网格k+1时间步的浓度Ck+1j代替 Cj，得到微分方程式（9）的FTCS隐式差分格式，进而形成以Ck+1j（j=1，2，…，Nx）为未知数的方程组；在施以边界条件后，上述线性方程组未知量个数和方程个数相等，均为Nx个，可表示为：

[a][c]={b}（20）

式中，[a]为系数矩阵；[c]为待求浓度列向量；{b} 为右端项列向量。对上述方程组求解程序在MATLAB环境下采用直接解法——追赶法实现。

3 结果与分析

为了对上述2种数值解法在强对流条件下求解ADE中所引入的数值误差（数值震荡和数值弥散）进行分析对比，对一个测试问题分别进行解析求解和数值求解，解析解作为比较基准，其中数值求解分别采用隐式有限差和特征线法，隐式有限差作为对照数值解法。通过将每种数值解法求解结果分别与解析解结果对比，可以评价分析各中数值求解方法引入的数值误差，进而对数值解法之间的数值误差及其方法优劣进行对比分析，以评价特征线求解法的性能和合理性。

3.1 测试问题 测试问题假定溶质运移是在一个等速均匀水流流场中进行的，且在初始时刻水中无任何溶质分布，在初始时刻开始一端连续注入浓度为C0的保守性示踪剂，溶质的对流扩散是一维的，相关数学模型[7]如下：

Ct=D2Cx2-uCx 0≤x≤+∞，t>0（21）

初始条件：C（x，t）|t=0=0 0≤x≤+∞（22）

边界条件：C（x，t）|t=0=C0

limx→+∞C（x+t）=0 t>0（23）

式中，C为溶质浓度，g/m3；D为弥散系数，m2/min；x为沿畦长坐标，m；u为水流流速，m/min；t为时间，min。

3.2 解析与数值求解

3.2.1 解析解。通过Fourier变换，可求得上述定解问题的解析解[7]。

C（x，t）=12C0[erfc（x-ut4Dt）+exp（x+ut4Dt）erfc（x+ut4Dt）]（24）

式中，erfc（x）为余误差函数；其他符号意义同前。

3.2.2 数值解。数值求解方法分别采用特征线法和作为对照的隐式有限差方法。数值求解输入参量有：研究域长度80 m，空间剖分单元数（Nx）=200，模拟时段为25 min，时步数（k）=200，水流速度（u）=3 m/min，注入溶质初始浓度C0为5 g/m3。

溶质运移参数弥散系数（Kx）用以下公式[10]计算：

Kx=CeCdngh5/6v（25）

式中，Ce为常数（无量纲）；h为水深，m； v为流速，m/min；n为糙率；g为重力加速度，N/kg；Cd为常数，m0.5/min。文中Ce取值为4，n为0.11，Cd为60 m0.5/min。

3.2.3 求解方法数值误差对比分析。

一个完整的数值模型由控制方程、定解条件和求解方法构成。在控制方程和定解条件既定的条件下，数值求解方法的不同影响模型的精度及其优劣。该文在相同时空域网格剖分及其他模型输入参数相同的条件下，对采用的特征线法和隐式差分法引入的数值震荡和数值弥散大小进行比较分析，以评价强对流条件下求解地表溶质运移方程ADE采用特征线法的合理性。

作为比较基准解析解结果没有任何数值震荡和数值弥散，而数值解则由于数值近似存在数值震荡和数值弥散，因此分别将特征线法和隐式有限差的求解结果与解析解结果对比，分析各自引入的数值误差状况。最后，就各自引入的数值震荡和数值弥散进行对比，以评价特征线法相对于对照解法的性能及合理性。

（1）特征线法。

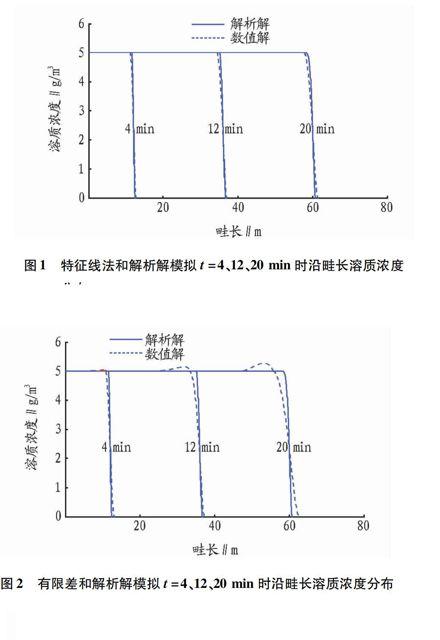
图1为特征线法与解析解模拟在时刻t=4、12、20 min时沿畦长的地表水流中溶质浓度分布状况。由图可知，特征线法与解析解模拟结果吻合性很高，因此特征线法引入的数值误差（包括数值弥散和数值震荡）很小，有效克服了强对流条件下的数值震荡和数值弥散问题。在t=12、20 min的过渡带（陡坡）曲线上，数值解曲线坡度略有放缓（比解析解结果曲线减少的坡度即是数值方法本身引入的数值弥散造成的，解析解过渡带曲线的坡度才是由物理弥散系数（D）的真实反映）。由此可知，随着时间的推移，特征线法求解结果的数值弥散变得更明显，但总体上数值弥散量仍很小；特征线法模拟结果曲线单调下降，平滑而无任何起伏，说明该解法不存在数值震荡问题。

（2）隐式有限差方法。

图2为隐式有限差方法与解析解模拟在时刻t=4、12、20 min时沿畦长的地表溶质浓度分布状况。由图可知，随着时间的推移，数值解曲线过渡带坡度与解析解结果差异变得更加明显，尤其是t=20 min时曲线，数值弥散现象较明显，这是数值误差的时间效应形成的；数值解在溶质浓度由高变低的突变处有较大的数值震荡现象，与数值弥散现象相似，数值震荡随着时间推移明显增大。由此可知，隐式有限差解法存在的数值震荡现象较明显，同时引入一定的数值弥散。

通过对特征性法和隐式有限差方法间数值误差的对比分析，可知特征线法求解引入的数值误差很小，存在轻微的数值弥散，而没有数值震荡现象；而隐式有限差会产生较明显的数值震荡现象，同时隐式有限差引入的数值弥散也较特征线法明显。因此，在求解畦灌施肥地表溶质运移方程ADE时，采用特征线法进行数值求解较合理，能够有效地解决强对流条件下数值求解引入的数值震荡和数值弥散问题。

4 结论

基于零惯量模型和一维ADE分别作为水流和地表溶质运移控制方程，利用有限差和特征线法进行数值求解，建立一维畦灌施肥地表水流溶质运移模型。特征线法和对照解法隐式有限差解法间的数值误差对比分析表明，特征线法能够更有效地解决数值震荡和数值弥散问题，而隐式有限差方法则引入较大的数值震荡和数值弥散，数值震荡现象尤其突出，而且特征线法是借助于Lagrange方法求解对流项而克服数值误差，而隐式有限差方法减少数值误差必须通过细化网格剖分，在实际应用中网格细化剖分却往往受到限制。因此，采用基于特征线法的地表溶质运移模型显然更合理。

参考文献

[1] SANTOS D V，SOUSA P L，SMITH R E.Model simulation of water and nitrate movement in a levelbasin under fertigation treatments[J].Agriculture Water Management，1997，32（3）：293-306.

[2] DILLION J，EDINGERMARSHALL S，LETEY J.Farmers adopt new irrigation and fertilizer techniques[J].California Agriculture，1999，53（1）：24-28.

[3] ZERIHUN D，SANCHEZ C A，FARRELLPOE K L，et al.Performance indices for surface N fertigation[J].Journal of Irrigation and Drainage Engineering，2003，129（4）：173-184.

[4] PLAYAN E，FACI J M.Border fertigation：Field experiments and a simple model [J].Irrigation Science，1997，17（4）：163-171.

[5] GARCIANAVARRO P，PLAYAN E，ZAPATA N.Solute transport modeling in overland flow applied to fertigation[J].Journal of Irrigation and Drainage Engineering，2000，126（1）：33-44.

[6] ABBASI F，SIMUNEK J，VAN GENUCHTEN M TH，et al.Overland water flow and solute transport：model development and fielddata analysis[J].Journal of Irrigation and Drainage Engineering，2003，129（2）：71-81

[7] 王洪涛.多孔介质污染物迁移动力学[R].北京：清华大学，2005.

[8] 李韵珠，李保国.土壤溶质运移[M].北京：科学出版社，1997.

[9] STRELKOFF T.SRFR20.51：A computer program for simulating flow in surface irrigation furrowsbasinsborders[R].USDAARS，Water Conservation Lab.，1993.

[10] ZERIHUN D，SANCHEZ C A，FARRELLPOE K L，et al.Performance indices for surface N fertigation[J].Journal of Irrigation and Drainage Engineering，2003，129（4）：173-184.

[11] ZERIHUN D，FURMAN A，WARRICK A W，et al.Coupled SurfaceSubsurface Solute Transport Model for Irrigation Borders and Basins.I.Model Development[J].Journal of the Irrigation and Drainage Engineering，2005，131（5）：396-406.

責任编辑 刘月娟 责任校对 李岩