地锚式悬索桥的静力可靠性分析
2015-10-21郭平
郭平
【摘要】大型实际结构的功能函数往往不能明确表达,针对这一情况,运用均匀设计方法产生具有有效性的样本集,结合神经网络能以任意精度逼近极限状态函数的特点,再引用一次二阶矩方法等基本求解方法与MIDAS的有限分析功能相结合,基于MATLAB软件编制可靠度分析程序,对地锚式悬索桥进行静力可靠度分析。
【关键词】神经网络;可靠度计算;悬索桥
引言
悬索桥作为一种缆索承重的结构,20世纪后期,桥梁工程取得了很大的技术进步,人们也开展了许多基于确定性结构参数的静力问题的研究。然而,在实际中,结构参数中存在着大量不确定性,悬索桥结构的受力状态及可靠性会受这些参数的影响,这些问题的解决需要借助基于可靠度的分析方法。蒙特卡罗法能够应用于大型复杂结构系统,但是计算量非常大,消耗大量的有限元分析时间。
近年来,神经网络技术由于具有良好的学习能力和推理能力,适合处理对大量数据进行分析、建立复杂的非线性映射等问题,已逐渐运用于各领域。本文引用前人的研究成果,将BP神经网络技术运用到悬索桥结构可靠度分析中,作为结构可靠性分析的一种参考方法。
1 BP神经网络
单层BP神经网络如图 1所示,图中为输入信号,表征各个信息对神经元刺激的强弱,或称之为权值,为神经元的阈值,是神经元的输出信号,其表达式为:
(1)
式中,为激活函数,表示神经元的输入-输出关系。
常用的传递函数,有线性函数、对数S型函数、双曲正切S型函数。
线性函数的表达式为
(2)
对数S型函数的表达式为
(3)
双曲正切S型函数的表达式为
(4)
在一般情况下,在隐含层均采用S型传递函数,而输出层可采用线性传递函数或者S型传递函数。
根据多层神经网络映射存在定理,理论上证明一个任意的连续函数都能与一个3层神经网络建立映射关系。因此一般选3层网络。在确定网络结构参数后,使用一定数量的表示结构性能的基本变量如结构尺寸、材料性质、温度、力等作为输入变量,而将所关心的结构上的作用效应如应力、 变形等作为输出变量组成训练样本训练,确定神经元间的权值与阈值。由于样本矢量各基本变量的物理单位不同,数值差距甚远,因此,训练样本一般先进行归一化处理。在训练过程中,通过对网络权值和阈值进行调节,使网络的输出目标尽量的接近期望目标,准确地模拟结构的响应。
2 可靠度分析
基于BP神经网络的一次二阶矩法是以结构可靠度理论为基础,将均匀设计方法、结构有限元分析、人工神经网络以及一次二阶矩法等理论与方法有效地结合起来,解决求解功能函数为隐式、高次非线性的大跨度桥梁结构可靠度问题。具体的实施过程如下:
(1) 确定桥梁结构基本变量的个数,并统计其特征,选择适当的均匀设计表得出样本点;
(2) 建立有限元模型,计算归一化处理后样本点处的结构响应值,以此为目标矢量和样本点共同组成训练样本;
(3) 建立BP神经网络模型,确定所采用网络的结构形式,利用训练样本训练网络;
(4) 利用一次二阶矩方法完成桥梁结构的可靠度计算。
3 工程实例
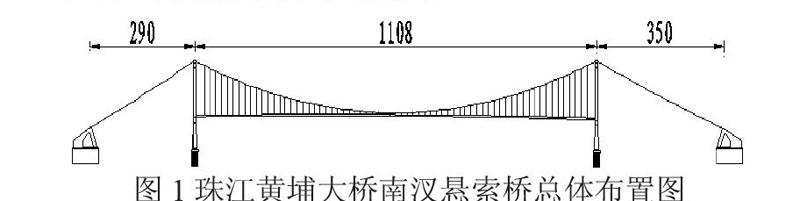
珠江黄埔大桥南汊桥是位于广州市的东郊。主桥为290m+1108m+350m的单跨双索面钢箱梁地锚式悬索桥,采用预制平行钢丝索股,主梁为带风嘴的闭口钢箱梁,梁高3.5m,全宽41.69m。图1为该桥的总体布置图。
图1珠江黄埔大桥南汊悬索桥总体布置图
采用有限元分析软件MIDAS建立考虑几何非线性的有限元模型,在正常使用极限状态下,主梁在汽车荷载(不计冲击力)作用下的最大竖向挠度为 (为中跨跨径),建立极限状态方程:
(5)
式中:为基本变量,包括结构上各种作用、材料性能、几何参数等。
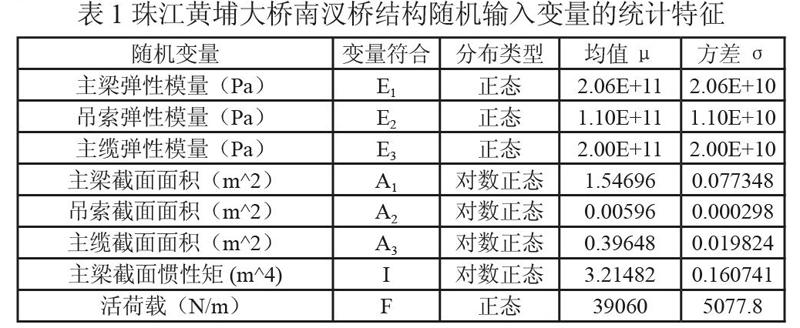
本文考虑的基本变量分别为主梁、吊索、主缆弹的性模量,截面面积,主梁截面惯性矩以及活荷载,其统计参数见表1。
表 1珠江黄埔大桥南汊桥结构随机输入变量的统计特征
随机变量
变量符合
分布类型
均值
方差
主梁弹性模量(Pa)
E1
正态
2.06E+11
2.06E+10
吊索弹性模量(Pa)
E2
正态
1.10E+11
1.10E+10
主缆弹性模量(Pa)
E3
正态
2.00E+11
2.00E+10
主梁截面面积(m^2)
A1
对数正态
1.54696
0.077348
吊索截面面积(m^2)
A2
对数正态
0.00596
0.000298
主纜截面面积(m^2)
A3
对数正态
0.39648
0.019824
主梁截面惯性矩(m^4)
I
对数正态
3.21482
0.160741
活荷载(N/m)
F
正态
39060
5077.8
选取8-8-1的BP神经网络结构,隐含层传递函数采用对数S型函数,输出层传递函数采用线性函数,选着适当的均匀设计产生的100个设计样本,建立起输入与输出的关系(即极限状态函数)。
为了验证神经网络拟合的准确性,按各参数的随机特征,随机产生30个检验样本点,利用有限元分析可以得到检验样本的真实极限状态函数值,并将检验样本点代入神经网络计算,可以比较其值,测试拟合的准确性,如图2所示。
然后利用一次二阶矩方法,计算得到的结构可靠指标为4.9731,通过有限元-BP神经网络-遗传算法计算得到的可靠指标5.021,结果比较接近,说明此方法可以提供作为参考。
图2检验样本下拟合函数计算值与真实功能函数值的比较
结 论:
大型复杂结构的功能函数一般不能显式明确表达,此时采用神经网络技术是进行可靠度分析比较方便的选择。本程序可以直接将可靠度分析与有限元分析结合起来,文中的工程实例分析验证了神经网络技术在可靠度分析中的有效性,能为工程应用提供依据。
参考文献:
[1]张明. 结构可靠度分析:方法与程序[ M].北京: 科学出版社, 2009.
[2]粟洪, 程进. 神经网络技术在预应力混凝土桥梁可靠度分析中的应用. [J].结构工程师,2009.
[3]谭红梅. 悬索桥施工仿真计算研究[D].博士学位论文,上海:同济大学土木工程学院,2009
