中学地理教学中数学思想方法的运用

周小桥

摘 要：学科之间的融合已成为一种趋势，地理学科横跨自然科学和人文科学两大领域，具有鲜明的综合性，为与其他学科之间的交叉奠定了基础；数学是科学的工具学科，数学思想方法是数学学科的精髓，是解决数学问题的基本手段。在地理教学中，在描述和解释地理现象上，缺乏科学的语言和论证过程；数学思想方法中的符号思想方法、集合论思想方法、数形结合思想方法、分类讨论思想方法、逻辑推理思想方法等，都可以应用在中学地理教学中，更好地解释地理现象、归纳地理规律。

关键词：数学思想方法；地理教学；符号思想

数学思想方法的种类和分类方式，各家说法不一。本文主要选取了中学数学中常用的五种一般数学思想方法，分别探究了这五种不同数学思想方法在高中地理教学中的应用。符号是描述数学研究对象的语言，集合是数学研究对象的形式表述，数形结合是数学两种基本研究对象之间的转换，分类体现了具体研究对象之间的异同与关系，逻辑推理是数学论证的基本方法。

一、符号思想

符号思想的实质是通过建立某种对应，实现从感性到理性的转换。符号的抽象程度和创造水平的高低差异直观影响学科的发展方向与速度；表达符号的不同也是对一门学科水平的反映。在地理学科中，我们可以借鉴数学学科的基本语言和符号思想，主要表现在以下几个方面：

首先，我们可以直接使用这些数学语言和符号，使地理学科的“理”性表达得更为简洁、科学，例如：正午太阳高度的公式：H=90°δ-？渍。满足了地理学，从定性的分析到定量的计算，公式的总结性表述，可以揭示地理事物的普遍规律，让学生可以更精确、概括性地认识地理现象。

其次，也可以借鉴数学语言和符号思想，发扬地理学科语言和符号，从而确立地理学科的独特地位。地理符号主要运用于地图教学。地图符号的建立需要严格的定义，要注重符号的科学性和合理性。地图上的符号大致可分为颜色符号、事物标志符号、文字符号和线柱符号。这些各种不同的符号，就是我们地理學科的形式化语言。在教学中，教师应该广泛地使用学科语言，给学生以潜移默化的熏陶，增强其对地理学科的归属感。

最后，素质教育的教学目标有三个维度，在知识的传递过程中，主要是对学生能力的培养和价值观的建立，这些目标可以通过地理学科符号来实现。地理符号除了教学中的狭义地图符号外，更包括人类长期以来的活动作用于环境的地理印记。在漫长的历史进程中，我们的祖先以其顽强的生命力和坚韧的毅力，不断同周围的地理环境相适应，并且改造地理环境，留下了人类活动的伟大印记，如天坛、长城、故宫、泰山等。这些改造自然的活动，不仅对地理环境进行了和谐的改造，而且将中华民族的文化精神和文化意识深深地浸染于其作用的地理印记之中，也就创造了具有丰富民族文化精神的地理符号。在地理教学中，对这些地理符号进行讲解时，一方面要让学生明白它们作为一些地理分界线或是特殊城市地理布局的知识含义；另一方面要让学生明白，地理符号是作为一种民族文化的载体，成为一种文化象征和文化精神。

综上可见地理符号在地理教学中的重要意义，因而在实际教学中，教师需要渗透地理学科的符号思想，让学生可以通过一种符号，认识一门学科，学会使用地理学科语言，并在这一过程中培养学生的综合素质。

二、集合论思想方法

人类关于集合的认识，一直都有一个很朴素的观念：把某类对象按照一定标准放在一起作为讨论范围。集合论思想方法就是指，运用集合论的语言和符号描述研究对象以及对象之间的关系，然后分析并解决问题的方法。集合论作为数学语言十分简单，数学概念都可以看做是集合，可以用集合论的语言来表述数学概念。

在地理教学中，集合论思想的应用对地理学科整体性把握更具优势；集合论的语言也可对地理概念进行简化；对于地理试题的解题方面，集合论的思想也将起到指导作用。

1.从集合论的高度概括中学地理内容，能更好地从整体上把握中学地理的研究对象

地理学起到的作用主要就是沟通自然科学和社会科学的桥梁作用，高中地理中必修一主要是自然地理学，必修二为人文地理学；自然地理中主要是根据地球的圈层结构，对课本进行编排；人文地理中主要是研究人口、人类的聚居地（城市）、人类生产生活（工业、农业）、对人类活动最重要的影响因素（交通）等。通过集合可以很好地表示高中地理的研究对象，让学生从整体上把握高中地理知识。

例如：

2.用集合论的语言表述有关概念更为简洁

地理中的专业概念较为繁多，很多概念在内涵上存在包含与被包含的关系，也有需要按照一定准则进行分类划分，借助集合的思想来表达地理中的概念，使抽象繁琐的语言表达显得更直观、形象，也更具有科学性。

例如：天体系统层次，用语言表达为地球所处的天体系统，按从低到高的级别，依次为地月系、太阳系、银河星和总星系。看起来很繁琐，借助集合知识表述为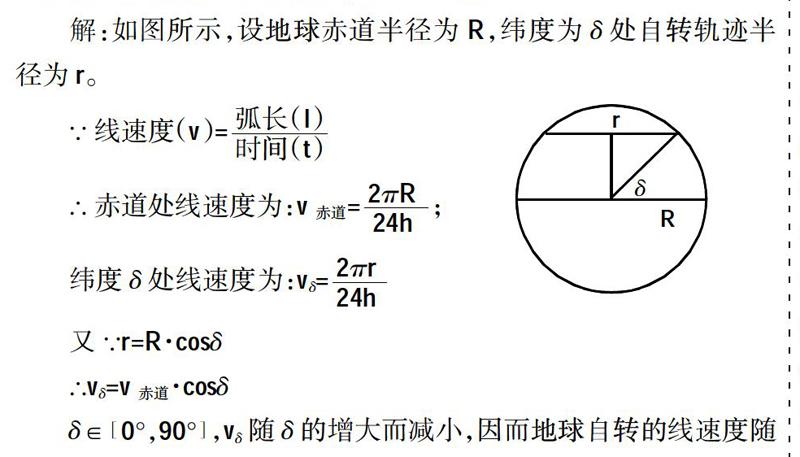：3.集合论的思想方法对解题的指导作用

运用集合论的思想对地理试题中的很多数学问题有着指导作用，以集合为工具，可将地理中涉及的几何、代数、三角等综合问题用几何形式表示出来，并提出解题思路。

案例一：地理概念

（1）从属关系：如，能源、一次能源、常规能源；土地资源、土壤资源、耕地资源。

（2）包含并列关系：如，降水、降雨、降雪；锋、暖锋、冷锋、准静止锋；淡水与各种陆地淡水资源。

（3）交叉关系：如，可再生能源、新能源、二次能源；自然资源、矿产资源、能源。

（4）排斥关系的概念：如，可再生资源和不可再生资源；岩浆岩、沉积岩、变质岩。

三、数形结合思想方法

地理学科最初的含义就是地图学，因此地理学科对图形的使用是普遍存在的，很多地理事物、地理现象和地理规律都是可以通过“数”与“形”归纳其本质属性的；其次，地理学科内容具有系统性，知识具有较强的逻辑性。在中学地理教学中应用数形结合的思想方法，可以培养学生的空间思维能力，结合地理学科特色，可以发展地理空间思维能力；数形结合思想方法的应用也可以使学生的形象思维与抽象思维能力得到提高，多种思维的互相促进，对培养学生灵活运用所掌握知识的能力有很大提高，对学生的综合能力有较大提高，还能为培养学生的创新能力奠定坚实的基础。

数形结合思想方法在地理学中应用的主要内容有：

（1）通过给出的图表，建立适当的代数模型；例如高中地理必修一中给出了太阳黑子数随时间的变化，通过图可以得出太阳黑子与时间的变化规律，发现太阳黑子活动的周期性。

（2）运用几何模型解答有关代数问题；例如时区和区时的计算，通过图形可以直观地看出世界不同地区所在的时区。

（3）与函数有关的几何、代数综合性问题；例如太阳高度角的计算，画出太阳直射点所在位置，结合几何与代数知识，可以很便捷地得出结果。

（4）以图像形式呈现信息的应用性问题；例如自然界的水循环示意图。

案例二：关于地球自转的线速度，课本上只是说明了：地球自转的线速度，因纬度的不同而有差异，那么学生该如何理解这种差异，即地球自转的线速度随纬度变化规律。

解：如图所示，设地球赤道半径为R，纬度为δ处自转轨迹半径为r。

∵线速度（v）=■

∴赤道处线速度为：v赤道=■；

纬度δ处线速度为：vδ=■

又∵r=R·cosδ

∴vδ=v赤道·cosδ

δ∈0°，90°，vδ随δ的增大而减小，因而地球自转的线速度随纬度的增大而减小；且当δ=60°时，v60°=■v赤道，也就是纬度为60°时，其线速度为赤道地区的一半。

四、分类讨论思想方法

分类讨论是指当问题中所给出的对象不能进行综合研究时，需要研究问题的对象按某个标准进行分类，然后每一类分别讨论，最后根据各类结果进行综合得到整个问题的答案，这种先进行分类再讨论，把复杂问题“分而治之，逐个击破”的解决问题的思想方法就是分类讨论思想。这种思想体现了化整为零、逐个击破，再积零为整的数学思想，反映了研究對象之间的内在规律，可以帮助学生总结归纳知识，提高学生思维的条理性和概括性。分类讨论时需要注意的是：每次分类时必须按照统一标准；分类讨论中的每一个部分要相互独立；分类讨论要注意层次，逐级进行分类，做到不重复、不遗漏。

地理作为综合性学科，地理事物导致的地理现象成因复杂，一个地理现象往往是多方面因素综合影响形成的结果，在分析地理现象时往往需要考虑多方面的因素，这会给我们的思维增加难度，因而可以通过分类讨论的思想，把复杂问题分化成多个简单的小问题。

引起分类讨论的因素较多，但常见的类型主要有以下几种：

（1）根据概念、公式、定理进行分类讨论；

（2）根据计算的要求进行分类讨论；

（3）根据地图的形状或位置变化进行分类讨论；

（4）当条件或结论开放时进行分类讨论；

（5）当问题中条件较少，需通过分类来补充条件时进行分类讨论。

例如，在讲解三圈环流：

第一步：假设下垫面性质均一，地球不自转、不公转；地球的大气环流形式为单圈环流。

第二步：去掉地球不自转的假设；形成了基本的三圈环流模型。

第三步：去掉地球不公转的假设；推导出了气压带和风带的季节移动。

第四步：去掉地球下垫面性质均一的条件；出现了气压中心。

案例三：“地球表面有适宜生命过程发生和发展的温度条件。”

对于这句话的理解我们可以引导学生从两个方面去考虑：

（1）如果地球表面温度过高，由于热扰动太强，原子根本不能结合在一起，也就无法形成分子，更不用说复杂的生命物质。

（2）如果地表温度太低，分子只能以晶体存在，生命物质也就无法形成。

五、逻辑推理思想方法

逻辑推理是根据已知的条件作出合乎逻辑的推断，推出未知的判断的一种思维方式。逻辑推理方式一般有三种：演绎、归纳和溯因。演绎推理主要是由前提得出必然的结论，由“前提”和“规则”推导出“结论”；归纳推理是从特殊到一般，借由大量的“前提”和“结论”所组成的例子来学习“规则”；溯因推理与演绎的过程相反，由“结论”和“规则”来支援“前提”，数学中常用的推理方式是演绎。在研究中，有学者发现中学生常用的证明和推理方法有：间接证明法和直接证明法；分析法和综合法；对比法和类比法；归纳法和演绎法。

在地理教学中，地理逻辑推理思想就是借助地理知识的相关概念，依照逻辑的规律推断出新的地理知识的思维活动。简单来说，是指借助地理概念，通过推理和判断，反映和揭示地理事物的内在联系和本质属性，从而获得对地理现象的规律性认识。地理学主要研究各种地理事物的空间分布及其成因和变化，而地理事物是相互依赖、相互联系、相互作用的，因而在中学地理学习过程中，可结合学生已具备的地理知识基础，运用逻辑推理的数学思想方法来研究诸多地理现象。

例如，高中地理必修一中，在探讨黄赤交角的变化对地球上五带的变化，教师可用逻辑推理的思想方法来讲解：

{目前黄赤交角：23°26′；南北回归线纬度：23°26′；极圈纬度：66°34′}

？圯{南北回归线纬度=黄赤交角，极圈的纬度=90°-黄赤交角}

？圯{黄赤交角变大}

？圯{回归线纬度变高，极圈的纬度变低}

？圯{温带将缩小，热带和寒带将扩大}

数学与地理起源相同，随着两个学科的发展日益壮大，学科之间可以相互借鉴、相互促进。地理学科横跨自然与人文两大领域，具有很强的综合性。在教学中，教师可以适当借鉴其他学科的思想方法，其中数学作为科学的工具性学科，对所有自然科学学科都有促进意义，因而在地理教学中应用数学思想方法，一方面可以解决仅用地理知识难以处理的问题，对学生学习地理知识、发现地理现象、探究地理规律，都能起到很好的促进作用；另一方面可以培养学生发散性思维和创新性精神，从而培养符合素质教育要求和适应社会发展需要的综合型人才与创新型人才。

本文举例主要涉及高中地理的自然地理，有关人文地理中的很多问题也是可以用数学思想方法解决。当然，数学思想方法并非唯一的一种方式，也并非是最有效的方式。在学科教学中，还有其他学科的思想方法，教师也可以在地理教学中适当应用。各个学科的思想方法都是学科的精髓，学科间的相互借鉴、融会贯通，学科的综合化是一种必然的趋势，教师在这方面需要有敏锐的判断力，为学生的终身发展奠定基础。

参考文献：

[1]吴炯圻，林培榕.数学思想方法：创新及应用的培养[M].厦门大学出版社，2009.

[2]于晓峰.地理符号与民族认同[J].社会科学家，2012（06）：150-152.

[3]张丹.关于高等数学与中学数学联系的探讨：集合论思想方法在中学数学中的应用[D].北京师范大学，1997.

编辑 温雪莲