国外松一元立木材积表的编制

谢华

摘要 以 923株国外松为编表样木， 选用5种数学模型为一元材积的候选模型， 利用非线性麦夸特迭代求解法确定各模型参数 、剩余标准差、相关系数等，确定最优模型为：V=0.000 130 0 d2.435 6；以 103株独立的验表样木进行总相对误差和F（0，1）检验，检验结果能满足林业生产材积估算误差要求，因此该表可为林业生产实践提供参考。

关键词 国外松；一元立木材积表；编制

中图分类号 S757.2 文献标识码 A 文章编号 0517-6611（2015）20-206-02

Abstract In 923 tree pine abroad for coding table like wood， a candidate model using 5 kinds of mathematical models for unitary volume， using the nonlinear Marquardt iterative method to determine the parameters of the model， the residual standard deviation，correlation coefficient and so on， to determine the optimal model：V=0.000 130 0d2.435 6； in 103 tree example wood experience independent of the total relative error and F （0，1） test， the test results can meet the requirements offorestry production volume estimation error. This table can provide reference for the forestry production practice.

Key words Foreign pine； Onevariable volume table； Compiling

国外松是1种优良的用材树种，安徽省从20世纪50、60年代引种栽植到80、90年代大面积造林，已得到了迅速推广。根据2005年安徽省森林资源规划设计调查统计结果表明，安徽省现有国外松林地面积99 204.47 hm2，蓄积4 751 276 m3，主要分布在宣城、滁州、巢湖等11个市的72个县（市、区）。

立木材积表是反映立木树高、胸径、形数等三要素与立木材积之间关系的数表，简称材积表[1]。立木材积表是最基础的林业数表，森林资源的计量工具，被称为森林资源调查监测的“度量衡”，在森林资源调查、采伐限额管理、森林经营成效评价、森林资产评估、林业执法等方面应用广泛。根据查定材积的变量数，主要分为一元材积表、二元材积表。一元立木材积表是反映胸径与立木材积关系的数表。多以省级林业区划的一级区为编表总体编制，主要用于森林资源连续清查（一类调查）、规划设计调查（二类调查）中查定立木材积，是立木材积表中，也是林业数表中研究最早、技术最成熟、应用最广泛的一种。到目前为止，安徽省尚无适用的国外松一元立木材积表。因此，编制国外松一元立木材积表， 以便为生产应用提供切实可行的技术保障。

1 基础数据收集

根据安徽省国外松的实际分布情况，分别在不同年龄和立地条件下设置国外松样地， 进行编表样木的调查， 该次共收集样木 1 320株，其中编表样木1 200株，在全部的样木中随机选取120株作为验表样木。

此次数表编制所需的样木分布在6～46 cm之间的21个径阶内，以 5 cm为起测径阶。样木伐倒后，以1 m为一区分段长，用围尺测量各区分段及胸高部位的带皮直径（精确到 0.1 cm），用皮尺测量树高 （精确到 0.1 m）。将外业所调查的胸径、树高及各区分段的中央直径，建立数据库， 并按中央断面积区分求积法计算各样木的材积。

2 数据整理

将各样木的胸径（d）、树高（H）及材积 （V）建立数据库作为此次编制和检验材积表的基础数据。

2.1 异常数据的剔除

异常数据的剔除过程分2步進行。首先， 分别绘制V-D散点图，通过肉眼观察确定出明显远离样点群的数据并删除；其次将用于编表计验表的样木分别按径阶计算其平均高（）、平均材积（）及相应的标准差（Sai），按照（）±3Sai将错误或异常数据剔除。

2.2 数据整理 剔除异常数据后，将所收集的全部样木分成编表样本和检验样本2组独立样本，其中最终编表的有效样木株数为923株，验表样木为103株。

3 一元材积表的编制和检验

3.1 编制一元材积表

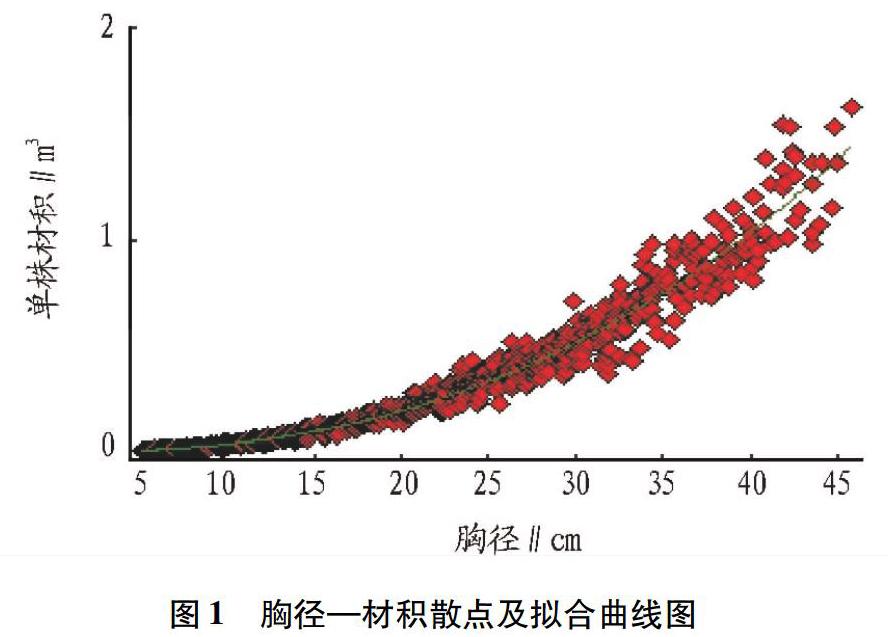
3.1.1 散点图的绘制。用图解法确定方程类型，将编表数据以横坐标为胸径，纵坐标为材积作散点图，根据散点图分布趋势，选择合适的方程模型，拟合结果见图1。

3.1.2 胸径—材积模型的选择。

3.1.3 模型的拟合结果与参数检验。

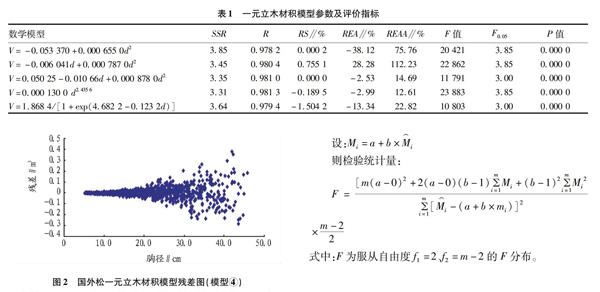
根据923株有效编表样木数据，利用DPS数据处理系统，采用非线性麦夸特迭代法[2]求解上述各模型参数，并计算各评价指标值，其结果见表1、图2。

由表1可以看出，5种初选模型的相关性都很高，其相关系数均在0.95以上，且模型显著性检验的F值均远远大于其临界值F0.05，显著水平P=0.000 0，达到极显著水平；同时各模型的总相对误差RS值均在（-3%，3%）范围内，说明以上各数学模型均为有效模型[3]。

由表1经对比分析可以看出模型④在5个方程中，其评价指标中相对误差绝对值平均值REAA、相关系数R、离差平方和SSR表现最好，其总相对误差RS、相对误差平均值REA也表现良好；通过各模型的残差分布可以看出，除模型④（图2）外，其他模型的残差分布在小径阶处均未以横轴为中心均匀分布，说明这些模型在模拟小径阶处的树干材积时会出现不同程度的偏差，因此根据前述模型选择的原则，综合考虑各评价指标，拟采用模型④作为此次编制安徽省国外松一元立木材积表的最优模型：

当F>F0.05时，推翻假设，说明a不等于0，b不等于1，检验样本实际值和估计值存在显著差异，胸径—材积数学模型不适用。当F≤F0.05时，说明a等于0，b等于1，检验样本实际值和估计值没有显著差异，胸径—材积数学模型适用。

3.2.2 模型适用性。当RS小于5%且大于-5%，同时通过F检验（F≤F0.05），则所建立并选择的数学模型适用，否则，应重新建模或选择其他模型检验。

3.2.3 模型检验。将独立采集的103株检验样木的实际胸径带入上述所确定的最优一元立木材积模型④中，计算检验样木材积估计值，建立检验样木的估计值—实际值的线性模型，获得上述指标中的参数值a、b，然后将相关数值分别带入上述2个指标的计算公式中，计算其指标值，结果表明：检验样本的总相对误差RS=-0.25%，在（-5%，5%）范围内；F（0，1）检验的F=0.11< F0.05（2，101）=3.09，说明检验样木实际值和估计值没有显著差异。

综上所述，利用模型④：V=0.000 130 0d2.435 6編制出的安徽省国外松一元立木材积表是适用的，能够满足林业生产的实际需要。

4 编表结果

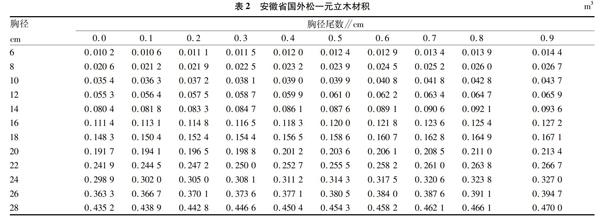
根据一元材积表回归模型V=0.000 130 0d2.435 6，求出相应的材积理论值，并将求算的材积理论值按对应的直径值整列成表，即得到安徽省国外松一元立木材积表（表2）。

5 结论

（1）材积表的适用性取决于编表和验表的样木数量及来源是否具有代表性，此次编表的 923株编表样木和 103株验表样木均来源于不同的年龄和立地条件，因此具有一定的代表性[5]。

（2）根据 923株编表样木数据，选取5种一元立木材积表的候选模型，用非线性麦夸特迭代求解法确定最优国外松一元立木材积表模型为： V=0.000 130 0d2.435 6。同时根据一元立木材积表模型估测材积的残差分析表明模型拟合程度较好[5]。

（3）用103株独立的验表样木进行总相对误差和F（0，1）检验。通过计算一元材积表理论材积与实际材积的总相对误差为RS=-0.25%，在（-5%，5%）范围内；F（0，1）检验的F=0.11< F0.05（2，101）=3.09，说明检验样木实际值和估计值没有显著差异。因此该研究编制的国外松一元立木材积表，可以为林业生产实践提供参考。

参考文献

[1] 孟宪宇. 测树学[M].2版.北京： 中国林业出版社，2008.

[2] 唐启义，冯光明.DPS数据处理系统[M].北京：科学出版社，2007.

[3] 孙岳胤，张文富.沙松人工林一元和二元立木材积表的编制[J].林业科技， 2004（5）：18-20.

[4] 宋英春.赤峰市低平地小冠型人工杨树一元材积表的编制[J].内蒙古林业调查设计，2015（1）：20-22.

[5] 周旭，杜传奇，唐雪海，等.杨树一元立木材积表的编制研究[J]. 安徽农业大学学报， 2008， 35（4）：486-489.