三角形截面钢管桁架人行桥人致振动舒适度评价
2015-10-21朱高波童金虎
朱高波 童金虎
摘 要:结构轻柔的人行桥受行人激振后会产生不同程度的振动,当振动响应达到一定程度时,就可能使桥上行人感到不适甚至引发恐慌。如何评估这种振动并将其控制在可接受的范围之内,是人行桥设计过程中需要考虑的一个问题,但国内规范对人行桥的人致振动舒适度尚无明确的评价标准。文章以一座结构新颖的钢桁架人行桥为例,介绍了《德国人行桥设计指南》对人行桥舒适度进行评价的方法,并提出了成桥实验建议。
关键词:人行桥;振动;时程分析法;舒适度
中图分类号:U441.3 文献标识码:A 文章编号:1006-8937(2015)08-0146-02
随着我国桥梁技术的进步,各种结构新颖的大跨径人行桥不断涌现,而随着桥梁跨径的逐步增加,结构刚度随之降低,人行桥的人致振动问题也日渐突出。人行桥的人致振动虽然会在一定程度上增加结构的荷载效应,但总的来说基本上还是一个舒适性的问题。关于人行桥的振动及舒适性问题,我国相关规范有“天桥上部结构竖向自振频率≥3 Hz”的规定。一般来说,将桥梁刚度提高到4倍才能使自振频率提高一倍,因此大跨度人行桥的自振频率要达到“≥3 Hz”这一标准是比较困难且很不经济的。我国现行人行桥设计规范在人致振动响应及行人舒适性的规定方面还有待完善。随着2000年英国千禧桥在开通当日发生的过度横向振动事件引起广泛关注,一些西方发达国家对大跨人行桥的人致振动理论及工程应用的研究已经走在了前列。德国人行桥设计指南(EN03,2007)(下文简称“德国指南”)在人行桥的舒适性评价方面已有较完整的规定。本文结合工程实际,依据德国指南,对一座较大跨径的三角形截面钢桁架人行桥的人致振动舒适度进行分析评价。
1 工程概述
1.1 总体布置
本桥由计算跨径为68.4 m的简支钢桁架主桥及两侧坡比为1?誜8的推行坡道引桥组成,桥面全宽5 m,桥梁全长164.83 m。桥型总体布置如图1所示。
主桥桁架的横断面呈三角形,如图2所示。该结构是在常规下承式钢桁架的基础上将两片主桁的上弦杆退化成一根上弦杆,取消了上平纵联,并将下弦杆间距适当拉开,在增强了桁架横向刚度的同时使桥面净空满足设计要求。该结构在纵向及横向均采用稳定的“三角形”构造,造型简洁,力学概念清晰,自重较轻而结构刚度相对较大。
1.2 主桥上部结构
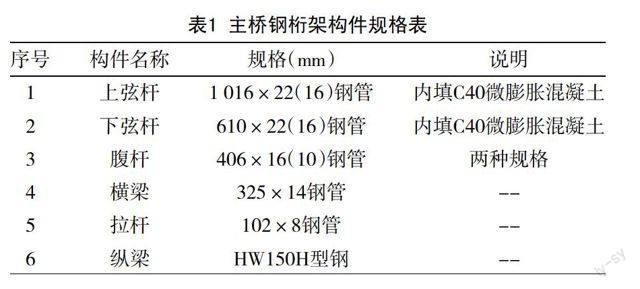
主桥桁架结构由上弦杆、下弦杆、腹杆、横梁、纵梁、下弦平面拉杆等组成,桁架计算高度为8.2 m,宽度为8.2 m,纵向节点间距7.6 m。上、下弦杆内灌填混凝土以提高桥梁整体刚度及钢管节点承载力。钢筋混凝土桥面板通过剪力键与桁架纵梁结合,结构厚度为12 cm,铺装厚度2.75~5 cm。主桥桁架主要构件均采用Q345C材质,构件规格详见表1。
2 动力特性分析
2.1 建模及假定
采用MIDASCIVIL2013有限元程序建模进行动力特性分析。上下弦杆内填充混凝土对提高结构刚度有一定效果,当完全计入上、下弦杆内所填充混凝土的刚度时,结构的基频可提高到2.4 Hz以上。考虑到钢管混凝土施工质量的不确定性,本次结构建模时偏安全的将上、下弦杆内填充的混凝土仅作为荷载考虑,不计结构刚度;12 cm厚的混凝土桥面板考虑结构刚度,而其上的铺装及栏杆仅作为荷载考虑,不计结构刚度。本桥结构自重较小,活载与恒载的比值相对较大,因此动力特性分析时,按照1.5人/ m2的分布密度(单人体重按80 kg计)考虑了行人荷载。上述荷载在动力特性分析时均转化为质量考虑。
2.2 动力特性分析结果
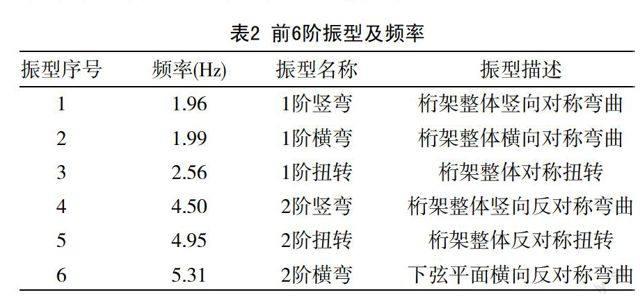
根据上述假定,对主桥上部结构进行动力特性分析,得到结构前6阶模态的频率及振型描述,见表2。
3 振动舒适性评价
当人行桥的固有频率范围在临界范围之内时,需要对人行桥的舒适性进行评价。德国指南采用人致振动最大加速度响应来评价人行桥的舒适度。最大加速度的计算可采用单自由度法、响应普法及有限元法等,本文采用有限元法進行计算。
3.1 舒适度验算的临界范围
人行桥竖向及纵向振动的敏感频率范围为1.25~2.3 Hz,横向振动的敏感频率范围为0.5~1.2 Hz。
另外,二阶行人谐波荷载也可能激发人行桥竖向振动(横向振动则不受影响)。因此人行桥舒适度验算的频率范围扩展为:竖向及纵向振动1.25~4.6 Hz,横向振动0.5~1.2 Hz。当人行桥的自振频率不在上述敏感频率范围时,一般可认为人行桥的人致振动问题自然满足要求。结合表2的动力特性分析结果,本桥第1、4阶振型主要表现为竖向振动,频率分别为1.96/4.5 Hz,应进行竖向振动的舒适度验算;第2、6阶振型主要表现为横向振动,频率分别为1.99/5.31 Hz,已不在横向振动敏感频率范围内,不需要进行横向振动的舒适度验算。
3.2 设计工况及等效谐波荷载
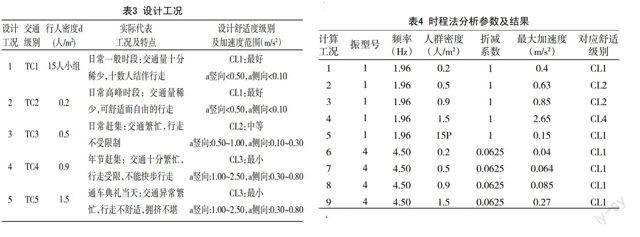
每个设计工况由一个预期的交通级别和一个选定的舒适度等级来确定,交通级别主要由桥上行人密度来表示。显然,重现率高的交通级别必须满足较高的舒适性水平,而重现率较低的交通级别可以采用较低的舒适度水平。根据德国指南并结合本桥的实际情况,本桥取用如下几种具有代表性的设计工况进行验证,见表3。
当行人密度超过1.5人/ m2时,行人基本不能行走,动力作用也会明显减小,因此可不考虑行人密度>1.5人/ m2的工况。对于有意识的以齐步队列行走的人群,设计不做验证,而是在交通安全设计时以禁令标志牌的形式予以禁止。
对于n个随机行人组成的行人流,可以用n'个完全同步的理想行人流来等效模拟。理想行人流按照下式(1)转换为均布谐波荷载p(t)[N/m2]:
p(t)=P×cos(2πfst)×n'×?追(1)
其中:
P为单人荷载幅值,横向取280 N,纵向取140 N,侧向取35 N;
fs为步频,假设它等于所考虑的人行桥某阶固有频率;
n'为加载面积为S时的等效行人密度:
TC1~TC3(人流密度d<1.0人/m2=:(1/ m2)(2)
TC4~TC5(人流密度d≥1.0人/m2):(1/ m2)(3)
T为结构的阻尼比;
n为加载面积为S时的行人数,n=S×d;
?追是考虑到步频接近基频变化范围临界值的概率而引入的折减系数。
3.3 结构阻尼
结构阻尼的大小对评估行人激振是十分重要的,但想要准确的估计系统阻尼却比较困难。系统阻尼的大小不仅与结构材料有关,而且还与振动水平有关,振幅较大时系统的阻尼一般也越大。
德国指南给出了不同材料类型的构造物在正常使用情况和较大振动情况下的平均阻尼比:正常使用状态下钢结构的阻尼比平均值为0.004,钢筋混凝土结构的平均阻尼比為0.013。
本桥上部结构由钢桁架及钢筋混凝土桥面系组成,计算时阻尼比取为:小幅振动时=0.005,振幅较大时=0.02。
3.4 时程法求解最大振动加速度及舒适度验证
时程法求解人行桥的最大振动加速度,就是将等效谐波荷载施加到结构的某一特定振型上,谐波荷载的加载方向与结构振动位移增大的方向一致,这样每个行人的作用都是使桥梁产生最大加速度。
根据动力特性分析结果,本桥需就第1、4阶振型对各种设计工况下的竖向振动逐一进行验证。各计算工况参数及结果见表4。
根据上表的计算结果,计算工况4,第1阶振型下当人群密度为1.5人/ m2时,人行桥振动最大加速度为2.65>2.5 m/s2(舒适度级别CL3的上限),不满足设计舒适度要求;其余计算工况可满足设计舒适度要求。
本桥横向刚度较大,固有频率在横向振动的敏感频率范围之外,一般不易触发横向锁定现象。
4 结 语
结构的阻尼比对人行桥人致振动分析结果的影响是非常显著的,而要精确预估人行桥的阻尼比却比较困难;另外,在进行有限元分析时,完全不计桁架上、下弦杆钢管内的混凝土刚度,这种有意识的削弱结构刚度的假设虽然趋于安全,但也会使有限元分析的结果与实际情况产生偏差。分析结果表明本桥在某些特定工况下的舒适度水平可能不满足设计要求,因此在桥梁建成后,用实验来测定人行桥的固有频率、振动模态及阻尼比等动力特性是必要的。在桥梁建成后,可根据实桥实验测定的动力特性来重新评估人行桥的振动响应,当确有必要时,可采取安装TMD(调谐质量阻尼)的方法增加结构阻尼,将人行桥振动响应控制在可接受的范围内。值得指出的是,本桥所采用的三角形截面钢桁架结构由于横向刚度相对较大,能在一定程度上减弱横向人致振动的不利影响。
参考文献:
[1] 陈政清,华旭刚.人行桥的振动与动力设计[M].北京:人民交通出版社,2009.
[2] CCJJ 69-95,城市人行天桥与人行地道技术规范[S].
[3] GB 50017-2003,钢结构设计规范[S].
