一类交叉耦合抛物型方程组解的爆破和整体存在性
2015-10-21吴春晨
吴春晨
(福州大学至诚学院计算机工程系,福建福州350002)
引理3 设u(x,t),z(x,t),w(x,t)满足式(1),且
一类交叉耦合抛物型方程组解的爆破和整体存在性
吴春晨
(福州大学至诚学院计算机工程系,福建福州350002)
分析一类交叉耦合的半线性抛物型方程组解的性质,通过构造上下解,讨论解的整体存在性和爆破,计算出方程组解的爆破临界指标。
交叉耦合半线性抛物型方程组;上下解;爆破临界指标
文中研究半线性抛物型方程组

式中:vn+1=v1;Bi>0;Mi>-2为实数;vi0(x)为定义在RN上的非负连续函数。
式(I)是对许多科学领域中出现问题的模型化。例如,渗流介质中的气体流模型,某些生物种群的增长模型。具有耦合形式的抛物型方程组解的性质是近些年来许多学者都致力探讨的问题[1-6]。Fijita[2]研究了一个方程的情形

并得到了很多有益的性质。
戴求亿[7]研究了2个方程的情况
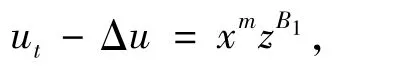
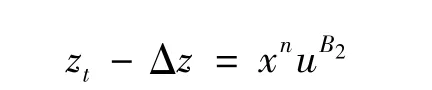
在文献[4-6]中,笔者已探讨了一系列由3个方程构成的关于拟线性抛物型方程组正解的整体存在与爆破性质,而在文中将进一步研究一类由n个方程构成的半线性抛物方程组。通过构造方程组的上下解,利用比较原理,运用类似文献[7-8]中的证明方法,得到式(I)的解在有限时刻爆破的充分条件。
1 主要结论
记
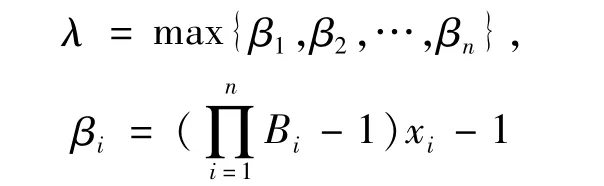
其中(x1,…,xn)T为下列方程组的解:

文中的主要结果为下列两个定理。
定理1 设vi0(x)≥0,且vi0(x)≠0 i=1,…,n,
2 定理的证明
文中只对3个方程的情形给予证明。一般情形的定理1和定理2的证明可用同样的方法得出。
考虑Canuchy问题
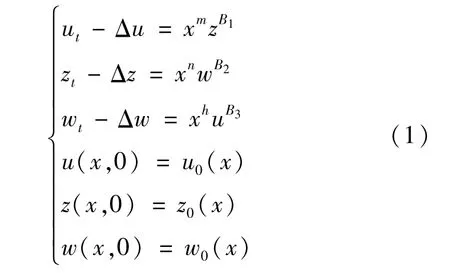
式中:(x,t)∈RN×(0,T),x∈RN;B1,B2,B3>0; m,n,h>-2为实数,u0(x),z0(x),w0(x)为定义在RN上的非负连续函数。
当3个方程的情况下,有
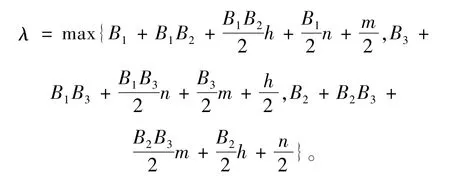
此时文中的主要结果可表述为:

先引入一个引理。
对于以下初值问题
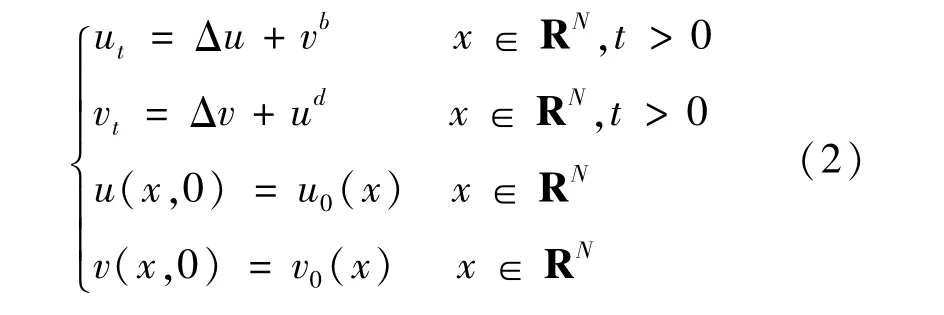
其中N≥1,b>0,d>0。

类似于文献[7]可证下列3个引理。
引理2 设u(x,t),z(x,t),w(x,t)满足式(1),则有:

其中,G为热算子的基本解:
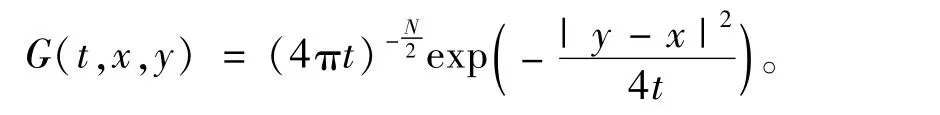
引理3 设u(x,t),z(x,t),w(x,t)满足式(1),且

则存在常数C,时间t1使得:
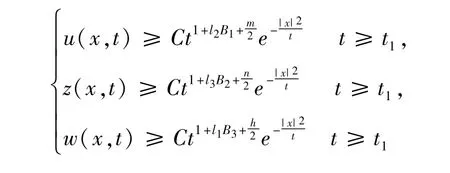
其中,x∈RN。

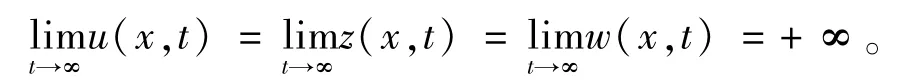
定理1的证明 设式(1)具有整体解,则由引理3可知,通过一个时间轴的平移变换,使得
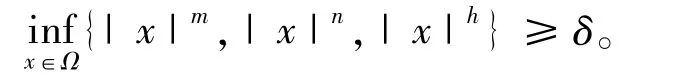
其中,设u0(x),z0(x),w0(x)充分大,选取有界区域Ω⊂RN。
考察初值问题:
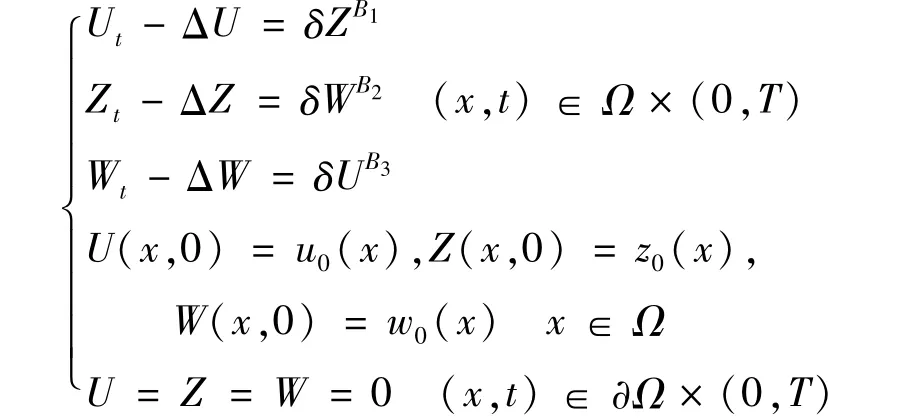
由比较原理可知:

又由文献[9]的结果可知,当u0(x),z0(x),w0(x)充分大时,U(x,t),Z(x,t),W(x,t)必在有限时间内爆破。因此,由式(3)可知,u(x,t),z(x,t),w(x, t)必在有限时间内爆破。
定理1证毕。
定理2的证明 有关爆破结论的证明与定理1的相同(详略)。下面给出解的整体存在性的证明。为此,寻找式(1)具有如下形式的上解:


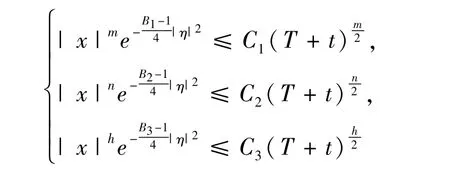
要使式(5)成立,只须使
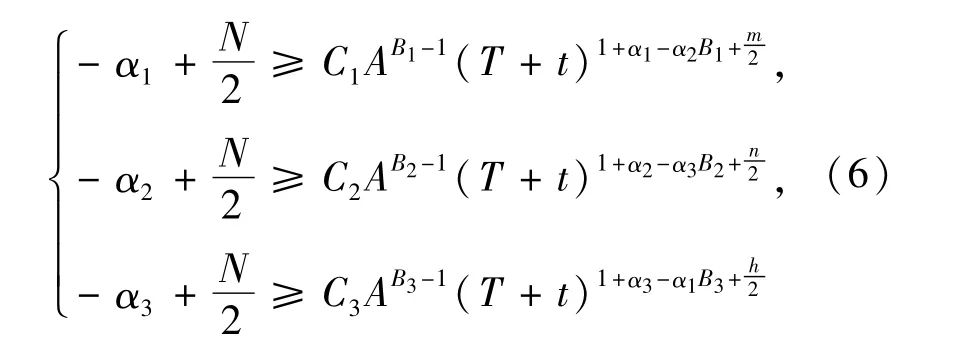
选取α1,α2,α3使得:
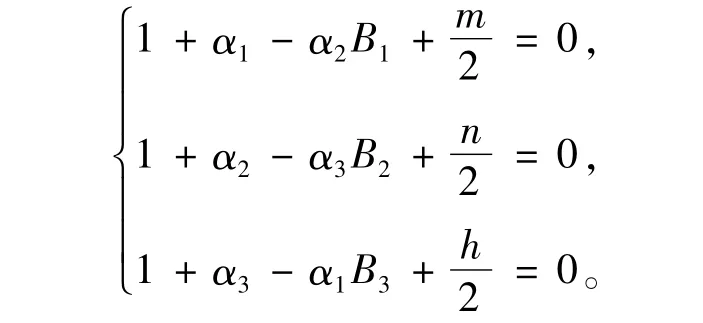
即

定理2证毕。
[1]李慧玲.一个非线性抛物型方程正解的性质[J].中国科学A辑:数学,2007,37(3):257-273.
LIHuiling.The blow-up property of positive solutions for a nonlinear parabolic equation[J].Science in China(A),2007,37(3): 257-273.(in Chinese)
[2]Fujita H.On the blowing up of solution of the cauchy problem for ut=Δu+u1+α[J].Fac Sci,Univ Tokyo Sect I,1966,13:109-124.
[3]陈玉娟.非局部退化拟线性抛物型方程组解的爆破和整体存在性[J].数学物理学报,2010,30A(2):386-396.
CHEN Yujuan.Blow-up and global existence for a nonlocal degenerate quasilinear parabolic system[J].Acta Mathematica Scientia,2010,30A(2):386-396.(in Chinese)
[4]吴春晨.一类非线性抛物型方程组正解的爆破[J].山西大同大学学报:自然科学版,2012,23(3):5-7.
WU Chunchen.The blow-up property of positive solutions for a nonlinear parabolic system[J].Journal of Shanxi Datong University:Natural Science Edition,2012,23(3):5-7.(in Chinese)
[5]WU Chunchen.Blow-up and global existence for a quasilinear parabolic system[J].Discrete Dynamics in Nature and Society, 2014(2014):1-4.
[6]吴春晨.一类交叉耦合抛物型方程组正解的爆破性质[J].福建工程学院学报,2012(6):7-10.
WU Chunchen.The blow-up property of positive solutions to a class of nonlinear parabolic equations with cross-coupling[J]. Journal of FuJian University of Technology,2012(6):7-10.(in Chinese)
[7]戴求亿.一类半抛物方程组的爆破临界指标[J].应用数学学报,2002,25(2):339-346.
DAIQiuyi.Blowing up critical exponent for a class of semilinear parabolic systems[J].Acta Math Appl Sinica,2002,25(2): 339-346.(in Chinese)
[8]Escobedo M,Herrero M A.Boundness and blow-up for a semilinear reaction-diffusion systems[J].Journal of Dynamics and Differential Equations,1991,89:176-202.
[9]Chlebik M,Fila M.From critical exponents to blow-up rates for parabolic problems[J].Rendiconti Di Matematica e Delle Sue Applicazioni,1999,19(4):449-470.
(责任编辑:邢宝妹)
Blow-Up and G lobal Existence of Solutions for a Certain Parabolic System w ith Cross-Coup ling
WU Chunchen
(Department of Computer Engineering,Fuzhou University Zhicheng College,Fuzhou 350002,China)
The solutions to the problems of a class of Semilinear parabolic equationswith cross-coupling are studied.By constructing the upper-lower solutions,we discuss the global exsistence and the blastibility of the solutions and the critical exponents are evaluated.
semilinear parabolic system with cross-coupling,upper-lower solutions,critical exponents
O 175.2
A
1671-7147(2015)03-0370-04
2014-11-05;
2015-01-03。
福建省自然科学基金项目(Z0511015);福建省教育厅A类科技项目(JA12374)。
吴春晨(1978—),女,福建福清人,副教授。主要从事偏微分方程研究。Email:wuchunchen@fzu.edu.cn
