一种新型滑模控制的有源电力滤波器

桑杰, 吴雷

(江南大学轻工过程先进控制教育部重点实验室,江苏无锡214122)

一种新型滑模控制的有源电力滤波器

桑杰, 吴雷*

(江南大学轻工过程先进控制教育部重点实验室,江苏无锡214122)

以三相三线制有源电力滤波器为研究对象,针对传统滑模控制在保证系统鲁棒性的前提下跟踪误差较大的问题,采用一种滑模控制与反推控制相结合的控制策略。首先建立并联型有源电力滤波器在αβ静止坐标系下的数学模型,然后设计反推滑模控制器,最后对其进行仿真和实验研究。仿真实验结果表明,反推滑模控制不仅使系统具有良好的鲁棒性而且有效地改善了跟踪误差。

有源电力滤波器;滑模控制;反推控制

随着国内外电力电子器件等非线性负载的广泛应用,电网中的谐波污染状况日益严重[1],谐波治理成为电力行业关注的焦点。由于有源电力滤波器具有良好的动态响应速度和补偿性能,在理论和实际应用中得到了快速发展。

有源电力滤波器的主要电流跟踪控制策略有无差拍控制、单周控制、空间矢量控制、反推控制等。无差拍控制解决了动态响应的问题,而且比较容易执行,但是计算量大,鲁棒性差[2]。单周控制具有控制精度高、控制电路比较简单等优点,但抗干扰能力差[3]。空间矢量控制开关频率稳定,但是由于具有复杂的坐标变换使得计算量比较大[4]。反推控制可以使系统得到全局稳定的性能,但是鲁棒性能不佳[5]。

采用一种滑模控制和反推控制相结合的控制策略[6],相比于传统的滑模控制方法响应速度更快、易于实现,并且在保证系统鲁棒性的同时进一步改善了系统的跟踪误差。

1 有源电力滤波器的工作原理

有源电力滤波器(APF)的工作原理如图1所示。APF首先通过指令电流运算电路得出补偿电流的指令信号;电流跟踪控制电路根据补偿指令电流信号驱动主电路产生补偿电流i。补偿电流i与负载电流iL中的谐波电流大小相同方向相反,从而达到消除谐波的目的[7]。

1.1 谐波电流检测原理

在APF的控制过程中,只有对负载中的谐波进行精确实时地检测才能对谐波电流进行精确地补偿。文中采用瞬时无功功率的检测算法,其算法流程如图2所示。主要是通过将dq轴上的电流经过低通滤波器得到有功基频分量,再用检测到的负载电流减去该有功基频分量得到所需要的谐波和无功分量[8]。目前APF直流侧电容电压大部分都采用PI控制,其中是参考值。工作原理即通过PI控制促使APF与电网直接实现能量交换,最终使直流侧电压恒定。

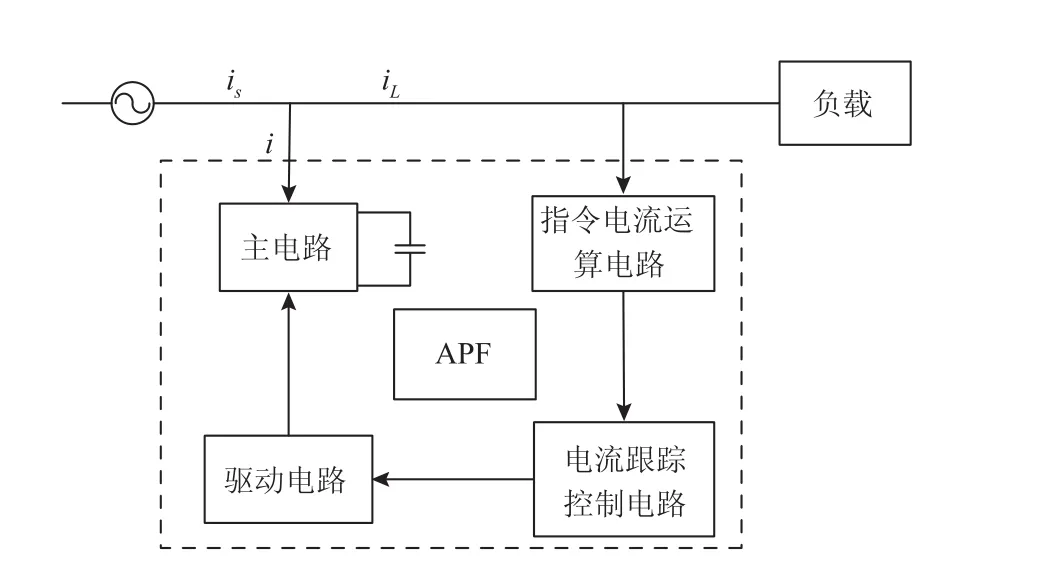
图1 APF的工作原理Fig.1 APF working princip le diagram

图2 ip-iq谐波电流检测方法原理Fig.2 Theory of the ip-iq detection method

1.2 有源电力滤波器的数学模型

三相三线制并联型APF拓扑结构如图3所示。

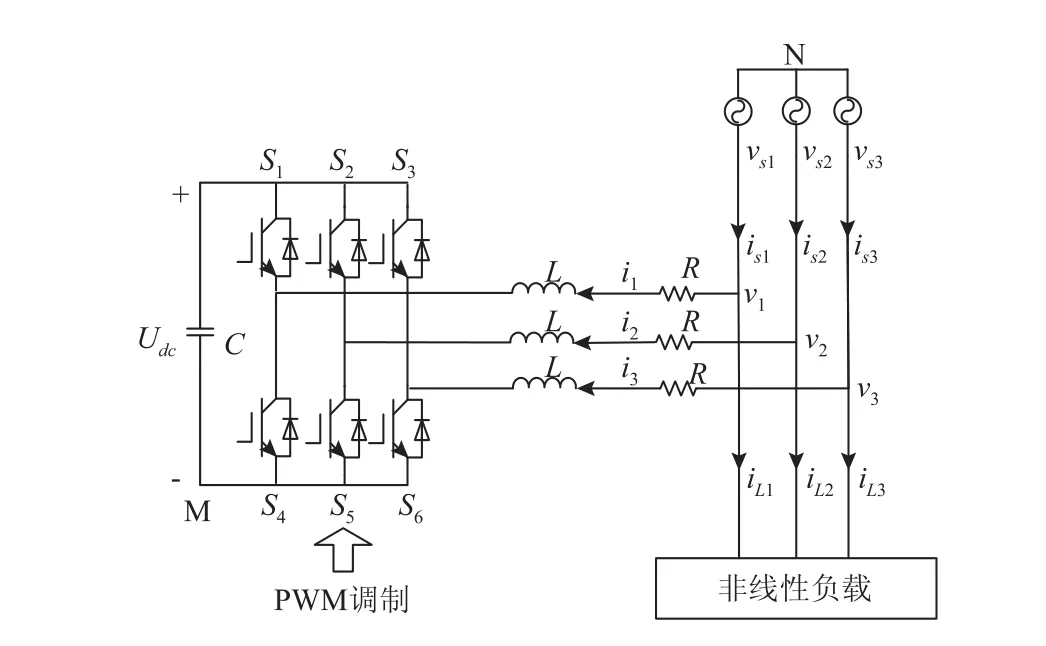
图3 并联型APF的拓扑结构Fig.3 Topology of the shunt APF

在三相电力系统中,电压和电流的参数都是三维,但在很多情况下这些电流和电压的参数均相关。为了简化系统的建模分析,引入αβ静止坐标系。两相静止坐标系下的状态空间模型如下所示:

其中:vα,vβ,iα,iβ,uα,uβ分别为公共耦合点电压v、补偿电流i和输出电压u在αβ静止坐标系下的电流和电压;C和Udc分别为直流侧电容和电容电压。

有源电力滤波器直流侧一般都选取比较大的电容,即电容两端电压变化相对iα,iβ非常缓慢,即可以忽略直流侧电容电压对iα,iβ的影响。

简化后的空间状态模型为

2 反推滑模控制器的设计

反推滑模控制的方法主要是在传统滑模控制的基础上加入反推控制。反推控制主要是通过控制Lyapunov函数使设计更加系统化、结构化。

2.1 反推滑模算法的实现

反推滑模控制器的设计主要包含两个部分:

(1)反推算法:通过建立Lyapunov函数和设计虚拟误差变量构造了一个新的子系统使整个系统稳定;

(2)滑模算法:通过构造切换函数S和确定滑模控制律使系统轨迹滑模切换面到达稳定点[9]。

1)跟踪误差定义为

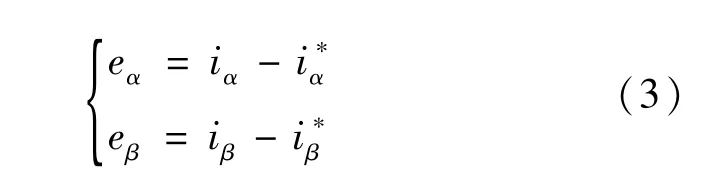
构造第一组Lyapunov函数为

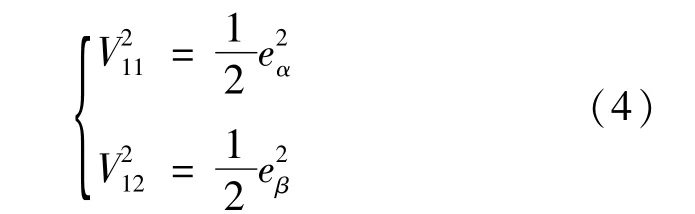
选择虚拟控制:

定义第二组误差变量为

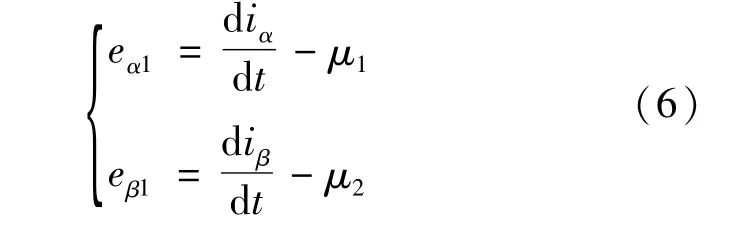
2)引入切换函数 通常切换函数采用的是各个误差变量的线性组合,而该方法不能保证系统的全局鲁棒性。为确保系统具有全局鲁棒性,在此基础上加入积分项与时变项。在整个动态过程中,为保证系统具有强鲁棒性,在切换函数中引入积分项。为使系统的状态能够在很短时间内到达滑模面,引入时变项:

其中,k3,k4,k5,k6,qα,qβ都为正常数,pα,pβ为常数, pαe-qαt,pβe-qβt为时变项。为实现系统的全局鲁棒性,必须满足系统初始时刻在时变滑模面上。这样就会有

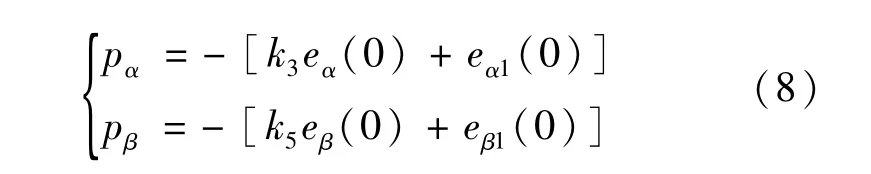
其中,eα(0),eα1(0),eβ(0),eβ1(0)分别为eα,eα1, eβ,eβ1的初始状态值。

构造第二组Lyapunov函数为

考虑到系统的全局一致渐进稳定性以及等效控制的存在性,最终推出反推滑模控制律为

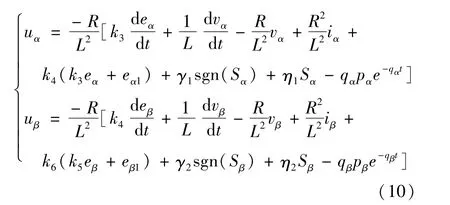
其中,γ1,η1和γ2,η2都是正常数,sgn()为符号函数。

2.2 控制系统框图

APF系统控制框图如图4所示。先通过反推控制获得全局渐进稳定,再通过滑模控制获得良好的鲁棒性。谐波电流检测采用比较成熟的瞬时无功ip-iq法。eα,eβ和eα1,eβ1是两组误差变量,滑模面是由两组误差变量建立起来的。最后由反推滑模控制律获得参考电压uα,uβ通过SVPWM控制开关管的关断与导通。

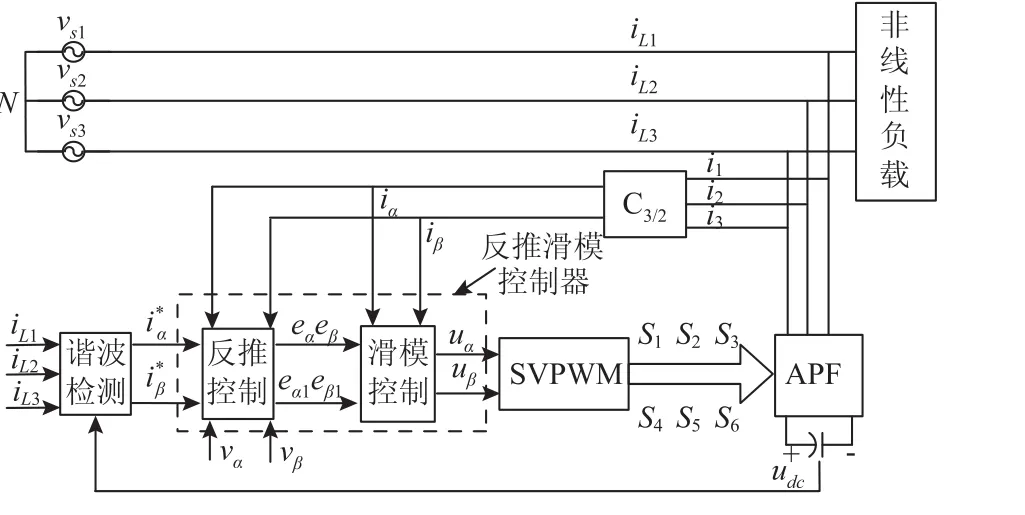
图4 APF系统控制Fig.4 Control block of the APF

3 仿真与实验

为了验证控制方案的正确性,搭建了Matlab/Simulink仿真模型。其仿真参数为:电网相电压220 V;频率50 Hz;非线性负载选用三相不可控整流桥,直流侧负载参数30Ω,20 mH;并联APF输出电感L=2.5mH,输出电阻R=1Ω;该系统的采样频率为100 kHz;运行至0.1 s时,负载侧串联一个串联阻感负载,其负载参数为15Ω,10 mH。该仿真中的常数为:k1=k2=0.5;k3=k5=0.5;k4= k6=100;γ1=γ2=1;η1=η2=2.5;qα=qβ=100。

系统补偿后的电网侧三相电流如图5所示。通过仿真波形可以看出,在0.04 s时投入APF使得波形已经接近理想的正弦波了,谐波含量明显减少。在0.1 s时改变负载,网侧电流能在很短时间内获得稳定,说明了系统的强鲁棒性。

图5 电网侧电流仿真波形Fig.5 Simulation waveform s of grid-side

实验所采用的是TMS320F2812 DSP作为主控芯片来验证控制方案的可行性。实验电路参数与上述仿真参数一致。

实验结果如图6所示(横轴t为每格5 ms,纵轴i为每格10 A),其中iL1为补偿前a相的负载电流, is1为补偿后a相的网侧电流,i1为a相的补偿电流。APF补偿后的电流总畸变率明显降低,改善了电能质量。因此验证了反推滑模控制方案的可行性。

图6 实验波形Fig.6 Experimental waveform s

4 结 语

根据传统控制策略的不足,将滑模控制与反推控制结合起来应用于APF中,通过仿真和实验验证了该控制策略的正确性,同时与传统的滑模控制相比除了具有良好的鲁棒性并且有效地改善了跟踪误差。因此这种控制方法具有很大的实用发展前景。

[1]王兆安,杨君.谐波抑制和无功功率补偿[M].北京:机械工业出版社,2005.

[2]王志良,王永,訾振宁,等.基于无差拍控制的有源电力滤波器研究[J].电力电子技术,2012,46(11):55-56.

WANG Zhiliang,WANG Yong,ZI Zhenning,et al.Research on deadbet control strategy of active power filter[J].Power Electronics,2012,46(11):55-56.(in Chinese)

[3]卞业伟,沈锦飞.基于单周控制三相四线制APF的研究[J].电力电子技术,2010,44(8):32-33.

BIAN Yewei,SHEN Jinfei.Research on the three-phase four-wire system APF based on one-cycle control[J].Power Electronics, 2010,44(8):32-33.(in Chinese)

[4]乐健,姜齐荣,韩英铎.一种新型的四桥臂三电平并联有源电力滤波器的空间矢量控制策略[J].中国电机工程学报, 2006,26(14):59-65.

LE Jian,JIANG Qirong,HAN Yingduo.A novel space vector control strategy of four-leg three-level shunt active power filter[J]. Proceedings of the CSEE,2006,26(14):59-65.(in Chinese)

[5]GE J J,ZHAO Z M,LI J J.Backstepping control for active power filter with LCL filter[C]//Renewable Power Generation Conference.Beijing:IET,2013:1-4.

[6]Carlos A Arellano-Muro,Luis F Luque-Vega,Castillo-Toledo B,et al.Backstepping control with sliding mode estimation for a hexacopter[C]//2013 10thInternational Conference on Electrical Engineering,Computing Science and Automatic.Mexico City: IEEE,2013:31-36.

[7]何志敏.并联型三相有源电力滤波器的滑模控制方法[D].长沙:中南大学,2011.

[8]朱日升,康劲松,卢文建.三电平有源电力滤波器的无差拍控制研究[J].电源学报,2013,5(14):14-20.

ZHU Risheng,KANG Jinsong,LUWenjian.Research on deadbet control strategy of three level active power filter[J].Journal of Power Supply,2013,5(14):14-20.(in Chinese)

[9]刘启宇.滑模反推式永磁直线同步电机控制策略研究[D].辽宁:沈阳工业大学,2010.

(责任编辑:杨 勇)

A New Sliding M ode Control for Active Power Filters

SANG Jie, WU Lei*
(Key Laboratory of Advanced Process Control for Light Industry,Ministry of Education,Jiangnan University,Wuxi214122,China)

Based on the active power filter of three-phase three-wire systems,aiming at the problems of large tracking error in the conventional sliding control in the premise of guaranteeing the robustness of the system,the slidingmode control strategy and backstepping technique combining is adopted.Firstly themathematicalmodel of shuntactive power filters is established inαβstatic coordinate,and then the back-stepping slidingmode controller is designed.Finally the emulational and experimental study is conducted.The emulational and experimental results show that the back-stepping slidingmode control can achieve good robustness and improve the tracking error effectively.

active power filter,slidingmode control,backstepping control

TM 712

A

1671-7147(2015)03-0295-04

2015-01-13;

2015-03-13。

江苏省产学研创新项目(BY2012069)。

作者简介:桑杰(1990—),男,江苏南通人,电气工程专业硕士研究生。

*通信作者:吴 雷(1962—),男,江苏无锡人,副教授,硕士生导师。主要从事电力电子与电力传动研究。

Email:wulei62622@126.com