基于ICA概率密度指标的过程监控

严文武, 潘丰

(江南大学轻工过程先进控制教育部重点实验室,江苏无锡214122)

基于ICA概率密度指标的过程监控

严文武, 潘丰*

(江南大学轻工过程先进控制教育部重点实验室,江苏无锡214122)

基于独立成分分析的多变量统计过程监控一般采用PCA方法的监控指标进行过程监控,并没有充分利用ICA方法特性。根据ICA分离得到的成分相互独立这一特性,提出了一种概率密度监控指标。用核密度估计的方法估计各成分概率密度,从而得到所有成分的联合概率密度,再根据联合概率密度判断过程状态是否异常。通过TE过程仿真表明,新的概率密度指标与传统指标相比,能检测出更多的故障点,监控效果更加有效。

独立成分分析;概率密度;监控指标;故障;TE过程

随着数据时代的来临,工业过程中大量的数据被采集并存储,但这些过程数据很多都未充分利用,导致“数据丰富,信息匮乏”现象的出现。因此,多变量统计过程监控和故障诊断技术受到学术界和工业界的广泛重视,并在化工生产过程中得以应用[1]。其中最为普遍的是主成分分析(Principal Component Analysis,PCA)和偏最小二乘(Partial Least Squares,PLS),并在化工、生物、制药等领域得到迅速发展[2-4]。

传统的PCA和PLS方法仅仅利用了低阶统计信息(均值和方差),然而在工业过程中常常存在非高斯信息,均值和方差无法全面描述其统计信息。基于PCA方法的前提是假设过程变量满足高斯分布且独立同分布,然而很多时候并不能完全满足这些假设;PCA只能去除相关性,并不能保证其独立性,同时一些观测数据中的隐变量也得不到有效估计[5]。因此,PCA和PLS方法有时效果并不是很理想。

基于独立成分分析(Independent Component Analysis,ICA)的多变量统计过程监控方法是由PCA方法进一步发展而来,该方法不要求变量满足高斯分布,能够有效地利用信号中高阶统计信息,提取的成分相互独立,更好地反应过程特征,从而更有效地进行过程监控。

基于ICA的多变量统计过程监控方法已有大量的文献对其加以改进。2009年,张晓玲等[6]提出基于非线性多向ICA的间歇过程监控方法;2010年,Yingwei Zhang等[7]提出一种基于PSO-ICA的非高斯过程故障检测方法,改善了ICA算法的分离效果;2011年,陆宁云等[8]提出基于时延SDG和ICA的多工况过程故障预测方法;2014年,李召等[9]提出基于小波去噪结合CVA-ICA的故障检测方法,主要针对工业过程含噪和随机干扰问题。

大多ICA监控方法的改进主要集中在对ICA算法自身的改进,少有针对ICA监控指标的改进。与传统PCA方法采用SPE和T2统计量类似,一般的ICA方法采用I2,I2e和SPE 3个统计指标进行过程监控[10],但没有充分利用ICA分离的成分相互独立这一特性。文中根据独立这一特性,各成分联合概率密度等于各单一成分概率密度的积,由此,提出一种概率密度监控指标(称作概率密度指标,记为P),并通过TE过程仿真验证其有效性。

1 ICA算法

独立成分分析(ICA)是信号处理领域在20世纪90年代后期发展起来的一种新处理方法,Kano等[11]首先提出了基于ICA的过程监控方法。

假设有d个观测变量x1,x2,…,xd可用m个未知独立成分s1,s2,…,sm通过线性组合表达。观测变量矩阵表示为x=[x1,x2,…,xd]T,独立成分矩阵表示为s=[s1,s2,…,sm]T,两者间有如下关系:

其中,A=[a1,a2,…,am]∈Rd×m是未知混合矩阵。ICA的基本问题就是根据已知观测数据x估计出混合矩阵A和独立成分s,等同于找一个解混矩阵W估计独立成分:

ICA基本原理如图1所示。

图1 ICA基本原理Fig.1 Basic p rincip le of ICA

求解独立成分的方法有很多,一般采用FastICA算法[12]。在计算之前要先对数据进行预处理,标准化数据后用PCA对x进行白化处理,消除数据间的二阶相关性,从而可集中分析高阶统计量。对x的协方差矩阵进行特征值分解:

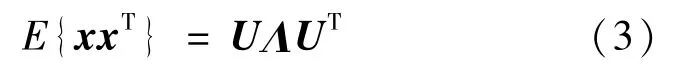
对x白化后有

其中白化矩阵

将式(1)代入式(4)有

其中,B=QA=Λ-1/2UTA,B为单位正交阵。对式(5)左乘BT可得

结合式(2)可知,W=BTQ,即只要求出B就能得到解混矩阵W,B可由FastICA算法求得。

2 概率密度指标

单变量统计过程监控时,正常状态下大量数值集中分布在其均值附近,越远离均值分布越少。根据样本统计原理设置控制限,超出控制限范围,就认为过程异常[13]。

多变量统计过程监控时,PCA方法采用SPE和T2统计量进行监控,而一般ICA方法监控[14]也采用类似统计量指标I2,SPE:

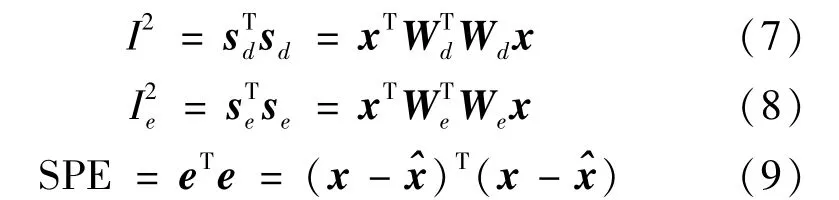
其中,Wd为W中影响s较大的d行,余下的几行为We。由于ICA提取独立成分的顺序是未知的,选择独立成分可以根据W行向量二范数大小进行排序,较大行作为Wd,较小行作为We。

上述指标来源于传统PCA多变量统计过程监控,没有充分利用ICA分离得到的成分相互独立这一特性。由于ICA方法提取的成分是相互独立的,则s联合概率密度可以通过下式求得:

式中:p(si)表示第i个独立成分的概率密度;m为总的独立成分个数。

由s联合概率密度可以得到全部独立成分的联合分布,这是一个多维空间分布。对比单变量统计过程监控,此处正常状态s数据大量分布于某一空间点(分布中心)附近,越远离这个空间点s数据分布越少。同理,根据样本统计原理可以设置控制限,超出控制限空间范围,认为过程异常。

为了实现ICA概率密度指标的过程监控,需要解决两个问题:①如何得到每个独立成分si的分布,即概率密度;②控制限空间范围的确定。

对于问题①,每个独立成分的概率可以通过核密度估计求得。给出一组给定样本数据X1,X2,…, Xn,则采用核密度估计方法的变量总体的概率密度为

其中,h为带宽(平滑参数);K为核函数。一般而言,核函数K的选取对核密度估计好坏的影响远小于带宽h的选取。文中核函数K选取常用的高斯核:

带宽h的选取是影响核密度估计精度的关键因素。h越小,估计结果越局限于观测数据附近;h越大,估计结果越平滑,当h不断增大,估计结果趋近于平均分布。通常h的好坏以均方误差衡量,文中采用Silverman的拇指法则(一种经验法则)计算最优带宽h

式中:σ为样本标准差估计;n为样本数。

对于问题②,多维空间的控制限空间范围没有很好的方法求解,即使求得这一空间也难以表示,不方便应用。

设置信度为(1-α),由于概率密度越远离分布中心值越小,则控制限空间范围的边界对应某一密度值Pα,该值满足以下条件:

式(14)表示所有小于Pα的概率密度积分为α。同样Pα也很难简单地通过公式求得,所以提出一种简单的方法估计Pα。当样本能充分反应其分布特性时,有下式:

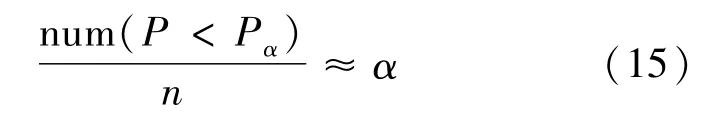
其中,n为样本总数;num(P＜Pα)为样本中概率密度小于Pα的个数。Pα的值可以简单地用样本中P值较小的a×100%处值近似代替。当样本较小时,可能出现代替值＞Pα的情况,这时可以适当减小。

记P为概率密度指标,Pα是该指标的控制限。当P≥Pα时,认为状态正常;当P＜Pα时,认为状态异常。其中,α的取值并不固定,可以根据实际情况进行调整,一般取0＜α≤0.05较为合适。

使用P指标绘制监测图时,由于Pα和故障状态P值都非常小,在图中很难看清,不直观。为了改善P监测图的直观性,取(-ln P)为纵坐标,控制限取(-ln Pα),然后再绘制P监测图,故障部分将被突出,直观性得到大大改善。

3 ICA概率密度监控过程

基于ICA概率密度的过程监控主要分为离线建模和在线监控两大部分。具体流程如图2所示。

图2 监控过程Fig.2 M onitoring p rocess

离线建模:对正常数据预处理后进行ICA分析,得到分离矩阵W和独立成分s,然后用核密度估计方法求得所有独立成分s的联合概率密度p(s),最后确定控制限Pα。其中Pα的值并不固定,该值的确定需要考虑具体的实际工况并结合实际效果作相应调整。

在线监控:在线数据根据已知分离矩阵W得到独立成分s,再根据离线建模概率密度p(s)求得对就P值,最后根据设定的Pα判断状态是否正常。

4 TE过程仿真

Tennessee Eastman(TE)过程基于实际工业过程,是一个标准测试过程。此过程被广泛作为连续过程的策略、监视、诊断的研究平台,有大量的文献引用它作为数据源进行相关研究[15-17]。该过程包括41个测量变量和12个控制变量,预设有21个故障,具体见文献[18]。

此次仿真选取500组正常状态下的前16个测量变量进行ICA建模,并对比各指标性能。控制限取分别取95%和99%。实际结果表明,这两种控制限对传统指标影响较小,对P指标影响较大。当取95%时,P指标故障误报数较高。以下实验,控制限都取99%(对于P指标,取正常状态从小到大排1%处值,此处为500组从小到大排第5个处的值)。

每种故障测试给出960组数据,前160组为正常状态数据,后800组为故障状态数据。以故障5为例,图3～图6分别为故障5的SPE,I2和P监测情况。

图3 故障5SPE的监测曲线Fig.3 SPEchartofFault5

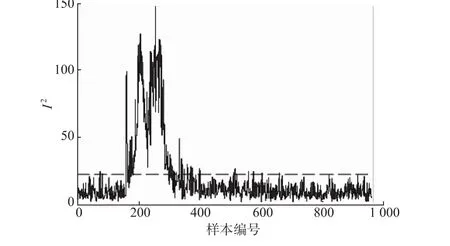
图4 故障5I2的监测曲线Fig.4 I2chartofFault5

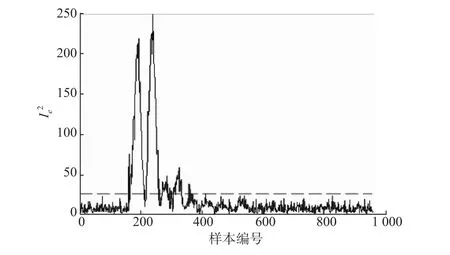
图5 故障5的监测曲线Fig.5 chartofFault5

图6 故障5P的监测曲线Fig.6 PchartofFault5

故障5总共有960个样本,故障在第160个样本后引入。4幅监测图中虚线为控制限,超出控制限的被认为是故障点。对于SPE,I2和监测图,分别检测的故障点数为199,159和140个。在图6中,大约第161到第300个样本间,其P值基本接近0,经处理后,(-lnP)值过大,未在图中显示。图6经过统计,全部故障区间检测到256个故障点。P指标相对于其他几个指标能检测到的故障点数更多,对故障更为敏感。

对每种故障的800个故障数据进行监测,表1给出了各故障不同指标检测到的故障点数。

表1 各故障不同指标检测的故障点数Tab.1 Numberoffaultdetectionbydifferentindicators foreachfault

由表1可以看出,P指标检测到的故障点数相对其他3个指标要多一点,尤其是某些相对难于检测到的故障。如故障4、故障9和故障15,P指标检测到的故障点数约是SPE,I2和的2～3倍。

表2给出了每种故障160个正常状态时误报的点数。

由表2可以看出,P指标误报数与传统指标误报数相近,但其检测到的故障点数明显要多于传统指标(即故障漏报较少)。

5 结 语

文中根据ICA分离的成分相互独立这一特性提出了一种基于ICA的概率密度指标P,并在TE仿真中证实了其有效性。该指标相比传统指标能检测到更多的故障点,故障检测率相对较高,该指标有一定的实际意义。概率指标也可应用于一些改进的ICA过程监控方法中,同样也能取得较好效果。

由于没有确切的科学证明指标肯定优于传统ICA指标,所以在使用时可以考虑结合传统指标共同参考,以达到较好的效果。

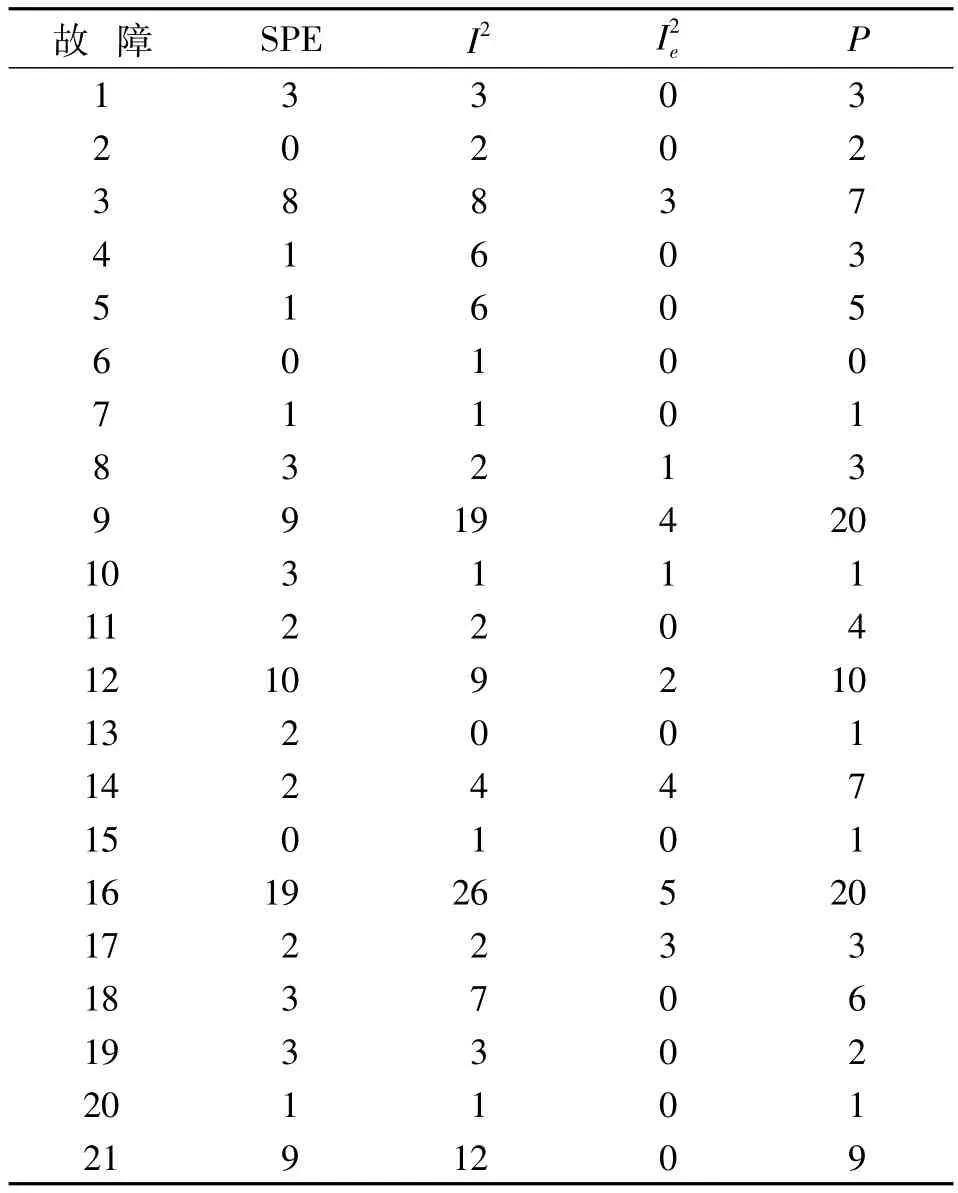
表2 各故障不同指标检测的故障误报点数Tab.2 Number of false alarm by different indicators for each fault

[1]YIN S,DING SX,Haghani A,et al.A comparison study of basic data-driven fault diagnosis and processmonitoringmethods on the benchmark Tennessee Eastman process[J].Journal of Process Control,2012,22(9):1567-1581.

[2]周东华,李钢,李元.数据驱动的工业过程故障诊断技术——基于主元分析与偏最小二乘的方法[M].北京:科学出版社,2011.

[3]LIU Q,CHAITY,QIN SJ,etal.Progress of data-driven and knowledge-driven processmonitoring and fault diagnosis for industry process[J].Control and Decision,2010,25(6):801-807,813.

[4]Joe Qin S.Statistical processmonitoring:basics and beyond[J].Journal of Chemometrics,2003,17(8/9):480-502.

[5]王海清,宋执环,王慧.PCA过程监测方法的故障检测行为分析[J].化工学报,2002,53(3):297-301.

WANG Haiqing,SONG Zhihuan,WANG Hui.Fault detection behavior analysis of PCA based processmonitoring approach[J]. Journal of Chemical Industry and Engineering,2002,53(3):297-301.(in Chinese)

[6]张晓玲,田学民.基于非线性多向ICA的间歇过程监控方法研究[J].系统仿真学报,2009(11):3365-3369.

ZHANG Xiaoling,TIAN Xuemin.Monitoringmethod based on nonlinearmulti-way ICA for batch process[J].Journal of System Simulation,2009(11):3365-3369.(in Chinese)

[7]ZHANG Yingwei,ZHANG Yang.Fault detection of non-Gaussian processes based on modified independent component analysis [J].Chemical Engineering Science,2010,65(16):4630-4639.

[8]陆宁云,王磊,姜斌.基于时延SDG和ICA的多工况过程故障预测方法[J].控制工程,2011,18(4):632-635.

LU Ningyun,WANG Lei,JIANG Bin.A fault prognosismethod based on time-dalayed SDG and ICA for multi-mode industrial processes[J].Control Engineering of China,2011,18(4):632-635.(in Chinese)

[9]李召,杨英华,李智辉.基于小波去噪结合CVA-ICA的故障检测方法的研究[J].仪表技术与传感器,2014(4):80-84.

LIZhao,YANG Yinghua,LI Zhihui.Fault detection based on wavelet de-noise and CVA-ICA[J].Instrument Technique and Sensor,2014(4):80-84.(in Chinese)

[10]Lee JM,Yoo C K,Lee IB.Statistical processmonitoring with independent component analysis[J].Journal of Process Control, 2004,14(5):467-485.

[11]Kano M,Tanaka S,Hasebe S,etal.Monitoring independent components for fault detection[J].AIChE Journal,2003,49(4):969-976.

[12]Hyvarinen A.Fast and robust fixed-point algorithms for independent component analysis[J].IEEE Transactions on Neural Networks,1999,10(3):626-634.

[13]钱夕元,荆建芬,侯旭暹.统计过程控制(SPC)及其应用研究[J].计算机工程,2004,30(19):144-145.

QIAN Xiyuan,JING Jianfen,HOU Xuxian.Research of statistical process control(SPC)and its application[J].Computer Engineering,2004,30(19):144-145.(in Chinese)

[14]樊继聪,王友清,秦泗钊.联合指标独立成分分析在多变量过程故障诊断中的应用[J].自动化学报,2013,39(5): 494-501.

FAN Jicong,WANG Youqing,QIN Sizhao.Combined indices for ICA and their applications tomultivariate process fault diagnosis [J].Acta Automatica Sinica,2013,39(5):494-501.(in Chinese)

[15]ZHANG Hui,FANG Huajing,LIShaxia.Fault diagnosis of the TE process based on discrete hidden Markov model[C]//2013 25th Chinese Control and Decision Conference(CCDC).Guiyang:IEEE,2013:4343-4346.

[16]徐圆,刘莹,朱群雄.基于多元时滞序列驱动的复杂过程故障预测方法应用研究[J].化工学报,2013,64(12): 4290-4295.

XU Yuan,LIU Ying,ZHU Qunxiong.A complex process fault prognosis approach based on multivariate delayed sequenxes[J]. CIESC Journal,2013,64(12):4290-4295.(in Chinese)

[17]ZHANG Yingwei,ZHANG Yang.Fault detection of non-Gaussian processes based on modified independent component analysis [J].Chemical Engineering Science,2010,65(16):4630-4639.

[18]Chiang L H,Braatz R D,Russell E L.Fault Detection and Diagnosis in Industrial Systems[M].London:Springer-Verlag,2001.

(责任编辑:邢宝妹)

Probability Density Index Based on ICA for the Process M onitoring

YANWenwu, PAN Feng*
(Key Laboratory of Advanced Process Control for Light Industry,Ministry of Education,Jiangnan University,Wuxi214122,China)

The process monitoring method with multivariate statistics based on independent component analysis(ICA)takes the process monitoring with indexes of PCA.It does not take full use of the features of ICA. According to the characteristic of themutual independence of the components separated with ICA,this paper proposes a processmonitoring index called the probability density index.The index estimates the probability densities of each componentwith the kernel density estimation in order to obtain the joint probability density.Then the joint probability density is used to judge whether the process state is abnormal.By the TE process simulation,it can make a conclusion that the new probability density index detects more fault points and is more effective comparing with the traditional indexes.

independent componentanalysis,the probability density,monitoring index,fault,tennessee eastman process

TP 277

A

1671-7147(2015)03-0283-06

2014-11-05;

2014-12-10。

国家自然科学基金项目(61273131);江苏省产学研前瞻性联合创新项目(BY2013015—39)。

严文武(1989—),男,江苏常州人,控制理论与控制工程硕士研究生。

*通信作者:潘 丰(1963—),男,江苏苏州人,教授,博士生导师。主要从事工业过程优化控制研究。

Email:pan_feng_63@163.com