筒式磁流变液联轴器的机理模型及特征解*

王贡献 张宇 胡志辉 周鹏中

(武汉理工大学 物流工程学院，湖北 武汉430063)

磁流变液智能材料具有瞬时可变可控性力学特性以及优良阻尼特性，被广泛运用到机械传动领域以实现传动系统特性控制. 鲁光涛等［1］研究了永磁型磁流变液联轴器工作间隙与传递转矩之间的关系，提出了磁流变液联轴器合理的工作区间隙选择依据;Wang 等［2］采用神经网络算法定性地模拟了磁流变液联轴器的非线性特性;韩晓明等［3］通过ANSYS 仿真研究了联轴装置重要几何参数对磁路性能的影响;申玉良等［4］设计了圆盘式磁流变离合器并基于实验数据提出了增大传递扭矩的方法;Wang 等［5］采用实验方法给出了MRF-132LD 型磁流变液直式阻尼器在冲击载荷下动力学参数-时间的动态特性关系;Wang 等［6］采用磁路耦合原理设计出一种永磁涡流联轴器，并着重研究了系统在冲击作用下的热能转换;Imaduddin 等［7］基于流体Bouc-Wen 等经典力学模型分析了不同形式的磁流变减振器所能传递扭矩与磁流变液本构属性间的关系;李宏男等［8］初步研究了磁流变(MR)阻尼器的基础理论模型及动态特性. 上述研究只是对磁流变液联轴器的磁路设计、几何尺寸及机械特性等某个方面进行理论分析，并通过数值方法和实验方法得到相关结论，未从系统的角度建立描述磁流变液联轴器的性能指标的理论模型和解析表达式，如最大传动力矩、相位转差、稳定时间、几何尺寸参数与磁流变液本构特性及其控制电流等之间的理论关系及其理论解.

文中以筒式磁流变液联轴器为研究对象，分析了机械动力传递过程中联轴器的运动学特性，得到了联轴器的最大传递力矩、稳定时间、可调倍数及其几何设计尺寸等关键参数的理论表达式.

1 联轴器的结构原理

图1 为碟筒式磁流变液联轴器结构图.联轴器由内腔和外部联接部分组成. 内腔由从动轴套筒(Ⅶ)包裹，其中的励磁线圈(Ⅵ)安置在线圈缠绕柱(Ⅴ)上，通过外接电源线(Ⅻ)完成电流供给;内腔与外部的主动轴套筒(Ⅱ)内壁之间的密封夹层放置磁流变液(Ⅳ)，为了增大屈服后的磁流变液切向剪切面积，在内套筒(Ⅶ)上适当开通轴向沟槽(す)，内支撑盖(Ⅲ)和密封盖(Ⅷ)保障了磁流变液腔的密闭性.联轴器在工作时外套筒(Ⅱ)与电机的输入端(Ⅰ)相连接，内套筒(Ⅶ)连接输出端(Ⅹ).

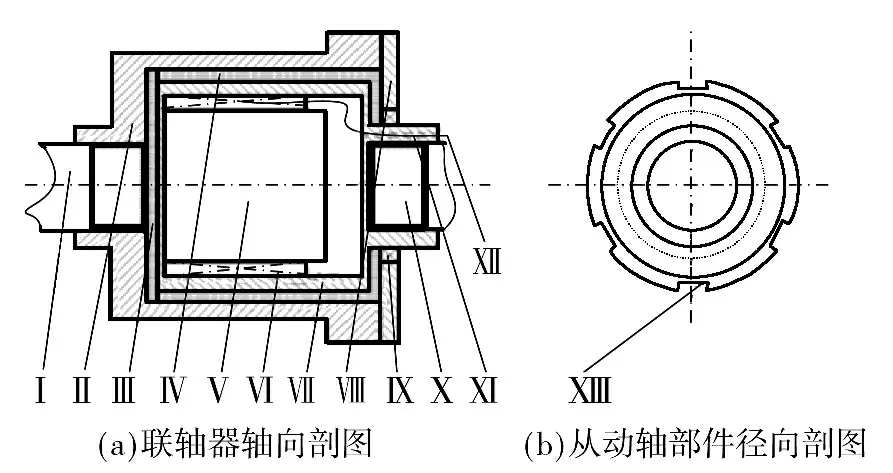
图1 磁流变液联轴器结构图Fig.1 Schematic structure of magnetorheological fluid couplings

励磁线圈中有电流通过时，工作区产生的磁场达到一定的强度，因为磁流变液的固液两相特性，该联轴器不仅能够传递扭矩，保证输入端和输出端的同步传动，而且有一定的柔性. 相较于传统连轴装置，该联轴器可通过延缓碰撞时间、增加相接触角位移的方式将一部分冲击动能转移到磁流变液的内部以热能释放，有一定的减振作用，同时减轻传动系统的物理冲击，延长系统部件的使用寿命;另外，联轴器的“软启动”特性可以实现较为平稳有效的起制动.

2 联轴器的力学原理

2.1 动力学模型

由筒式磁流变液联轴器组成传动系统是一个双自由度的线性振动系统.如图2 所示，T 是电动机驱动力矩，M 是负载阻力矩，Me是磁流变液联轴器等效扭转力矩，c0、k0分别为联轴器的等效回转阻尼系数和等效回转刚度，θ1、θ2分别为在磁流变液上的激励电场工作时电机及其他驱动系统和负载的角位移，J1为包括电机、驱动系统和磁流变液联轴器与主动轴联接部分的转动惯量，J2为负载和磁流变液联轴器与从动轴联接部分的转动惯量.该线性系统中分别作用在输入端和输出端上的转矩运动微分方程为

联轴器上传递的力矩［9］

θ 为运动过程中输入端与输出端的相对相位转差.

图2 筒式磁流变液联轴器动力传递模型Fig.2 Power transmission model of cylindrical magnetorheological fluid couplings

2.2 联轴器的等效刚度系数和阻尼系数

联轴器的具体磁路设计如图3 所示，根据安培定理有

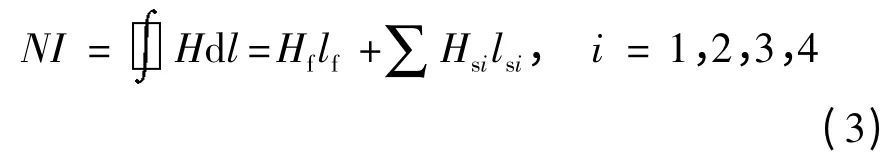
式中，N 为励磁线圈在内套筒内的绕线柱上的线圈匝数，I 为励磁线圈内的实时电流强度，Hf为在磁流变液流体区域的磁场强度，Hsi、lsi(i=1，2，3，4)依次为受励磁线圈影响的主动轴套筒部分、从动轴套筒部分、联轴器钢材内部的轴向部分和径向部分的磁场强度和线圈环绕有效线性尺寸，结合磁路结构形式有ls1=ls2=ls3=L，ls4=R2，L 为工作区轴向有效长度.线圈在磁流变液内线性环绕尺寸lf=R1-R2，其中R1、R2分别为磁流变液腔外径和内径，且主/从动轴套筒壁设计尺寸相同，认为均是R0-R1.

图3 磁路设计示意图Fig.3 Schematic diagram of magnetic circuit design

由以上几何关系结合式(3)可得到磁场强度与电流(H-I)关系，即

磁流变液联轴器的等效转动惯量

式中:JM为输出端转动惯量;JL为输入端联轴器外固有转动惯量;JZ、JC分别为联轴器与主动轴和从动轴相连接部分的转动惯量;m1为磁流变液的质量;r 为磁流变液与回转轴中心距离，这里可取中心距离r=(R1+R2)/2;rw为缠绕线圈中心与回转中心距离，rw=r0;mw为线圈质量.

联轴器的等效扭转刚度系数［9］

其中G 为磁流变液屈服后的剪切模量［11-13］，

式中，φ 是磁性颗粒的体积含量，μ0是真空磁导率，Ss为饱和磁化强度，μ0Ss为粒子的饱和磁强度.

综合式(4)、(6)、(7)可以得到磁流变液联轴器在不同励磁电流下的等效扭转刚度系数.

磁流变液的等效阻尼系数［9］

式中:ζ0是磁流变液的阻尼率，ζ0=ζA0-ηI，η 为系数，通过实验数据可取ζA0仅与磁流变液本构特性有关，一般有0.05 ＜ζA0＜0.35［9］;Cc为临界阻尼系数

3 联轴器的性能指标

3.1 相位转差和稳定时间

该联轴器传递的系统在制动过程中，由于磁流变液的固液两相性，输入端和输出端由于制动瞬间的同步转动而出现相位差，经过一定的制动稳定时间t1后完成制动.稳定时间反映了联轴器的工作时间效率，在满足工作要求的条件下，稳定时间增加可在一定程度上减小冲击对系统部件造成的损害. 为具体描述这一过程，引入两端相位转差θ =θ1-θ2，它反映了磁流变液联轴器的扰性强弱，即在制动时间相差很小的前提下，转差θ 能达到的最大值越大，联轴器所能吸收的冲击能量越多.

以θ 作为传动系统的自由度，在一定的输入转矩载荷下，式(1)、(2)的微分方程组可写作式(9):

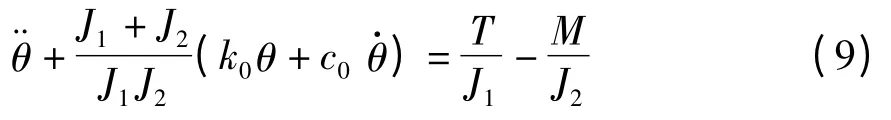
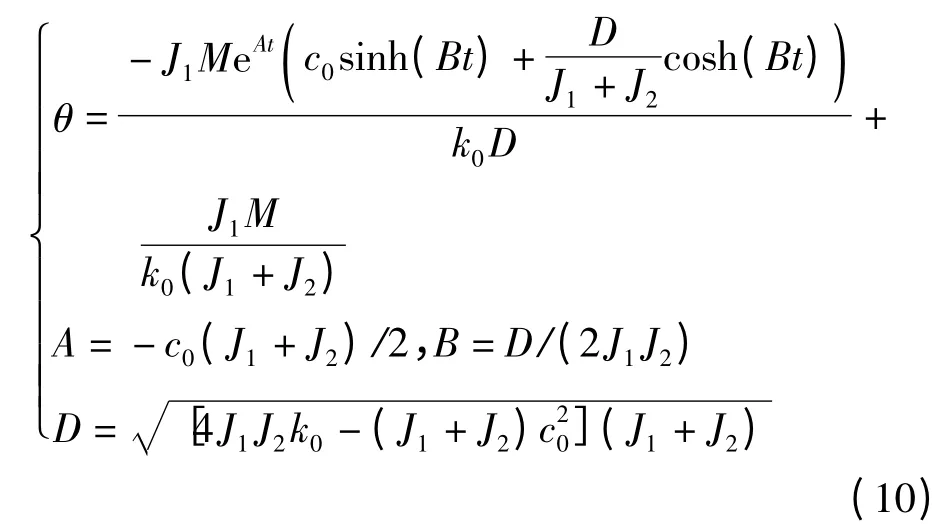
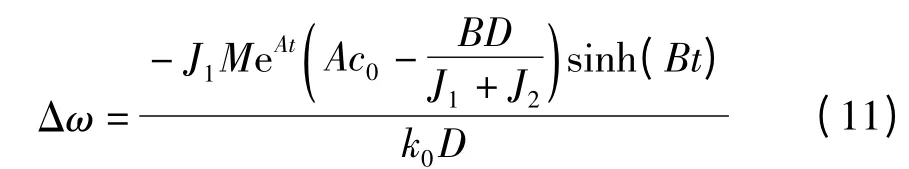
达到完全制动的条件为两者的速度差Δω 为零.类似地，当系统起动时，存在初始条件角位移差瞬间角加速度差系统在起动过程中的角位移-时间解析式为

式中，参数A、B 和D 的意义同式(10).输入、输出两端在此过程中的转速差为

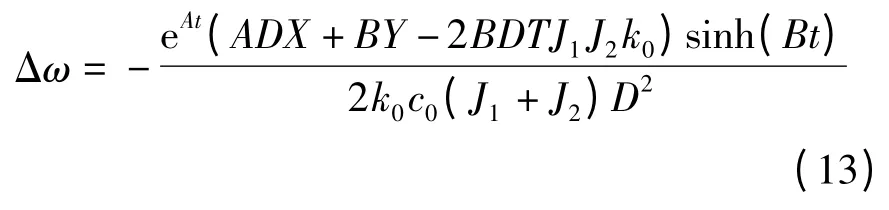
当转速差Δω=0 时达到稳定工作状态，需要用的时间为

3.2 最大传递扭矩

图4 是磁流变液联轴器转矩计算示意图，内筒与外筒间为磁流变液.若系统传动力矩以角速度ω1旋转，磁流变液受剪切力以角速度ω(r)转动，从而带动输出轴以ω2旋转.

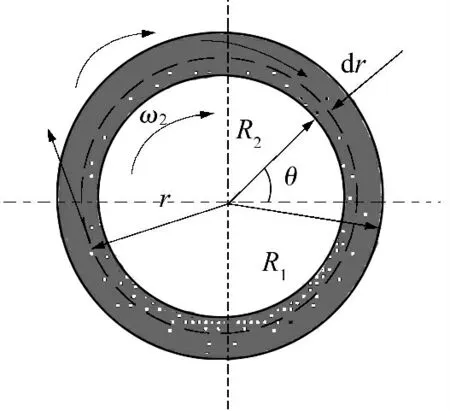
图4 磁流变液联轴器转矩计算示意图Fig.4 Schematic diagram of torque calculation of MRF couplings

根据速度边界条件

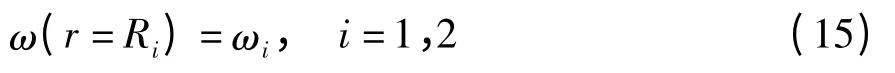
磁流变液的剪切应力与剪切速率关系如下［12-13］:

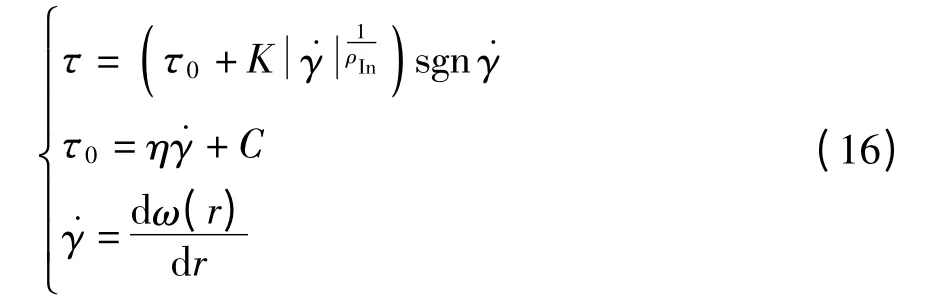
式中:˙γ 为磁流变液的剪应变率;ω 是磁流变液在处于稳态回转时的角速度;ρIn是与磁流变液本构特性相关的参数，反映了液体的等效黏度;0为零场剪切应力;η 是磁流变液塑性黏度;C 为常数.

圆筒间剪切流的动量方程为

在半径r 处，磁流变液所产生的扭矩为

由式(17)、(18)可得到磁流变液在两圆筒间作剪切流动的角速度为

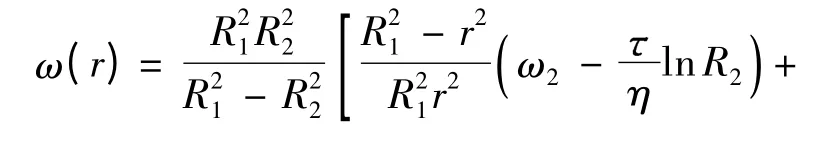
由式(18)、(19)可得到联轴器所能传递的扭矩

考虑到实际情况，该联轴器所传递的力矩T 应由3个部分组成［15］，分别是由结构自身等因素导致的摩擦力矩Tfr、由磁场作用形成的磁致力矩T 和磁流变液在磁致屈服后的自身黏度所引起的力矩Τη.在不考虑额外摩擦力矩Tfr的情况下，式(20)中的前后两项分别为动态屈服应力传递的扭矩T 和粘性力传递的扭矩Τη，即

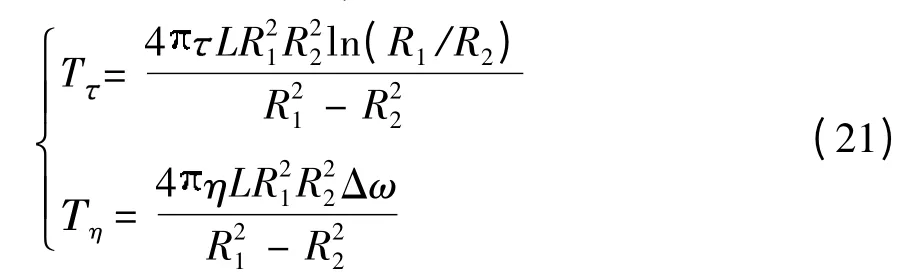
式(21)表明，粘性力所传递的扭矩除了与联轴器结构尺寸和磁流变液的本构参数粘滞系数η 有关外，还与筒间转速差Δω 有关.当系统从起动或制动状态趋于稳定后，联轴器所能传递的最大稳定扭矩Ts=T .记根据极限即当内套筒外径与外套筒内径无限接近时，在理论上的稳定扭矩最大，即

可以看到在设计联轴器时应尽量使得外筒和内筒的半径相差较小，以得到大的回转半径.

3.3 扭矩可调倍数

联轴器的可调倍数是该部件性能优良的主要指标之一，它反映了除联轴器尺寸参数外，仅与励磁电流形成的磁场强弱有关的库仑阻尼扭矩T 和仅与磁流变液的塑性黏度系数有关的粘滞阻尼扭矩Tη的比例关系.参考式(21)中的扭矩计算结果，有

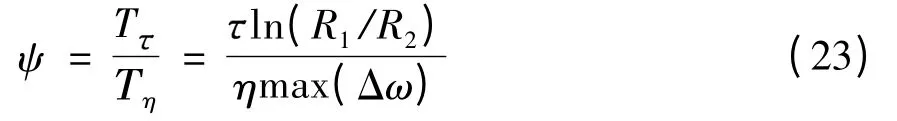
易知，在系统运行至稳定状态这一过程中，可确定主动轴和从动轴的最大转速差、可调倍数仅与联轴器的径向尺寸相对关系有关.

3.4 联轴器的关键几何参数

为了能够定量分析磁流变液联轴器的等效刚度系数和阻尼系数，以及系统的相位转差、稳定时间和扭矩可调倍数等关键参数，需要完善联轴器重要尺寸参数的设计方案.

在满足额定传递扭矩Te的条件下，根据式(22)，以min{max{L，R1}}为双目标函数建立线性优化模型，得到最节约空间的联轴器理论计算几何参数Ld、R1d，根据式(21)，取R1=R1d，R2=R1d-0.01 m，得到设计联轴器使用长度

所需磁流变液的体积V 对联轴器的成本估算有参考作用，如式(25)所示:

4 筒式磁流变液联轴器的应用实例

4.1 联轴器结构设计及分析

以常用的MRF-132DG 型磁流变液为例，若该联轴器需要传递额定扭转力矩T=3000 N·m，输入端电机额定转矩735 r/min.Lord 公司官方网站提供的磁感应强度-剪切应力实验数据如图5 所示［16］.

图5 MRF-132DG 磁流变液剪切特性曲线Fig.5 Shear properties of MRF-132DG

为了描述联轴器的动力学特性，这里将依据联轴器外形尺寸计算得到的所需电流强度最优化后的各重要参数数据定为A 组.根据式(22)、(24)，取安全系数=1.1，得到磁流变液联轴器重要理论尺寸参数，即参与磁场作用的磁流变液部分轴向长度L和磁流变液腔的最大、最小半径(R1、R2，)从实际工程尺寸考虑，优化条件可选为2R1＜L ＜3R1，如图6所示.

联轴器达到稳定工作状态时，由式(4)知不同电流形成的磁场下，相应的磁流变液获得不同的磁致屈服剪切应力;根据式(6)得到联轴器等效扭转刚度k0;根据式(8)得到联轴器等效扭转阻尼系数c0;根据式(23)可以得到联轴器的扭矩可调倍数.A组各数据对应列于表1 中.

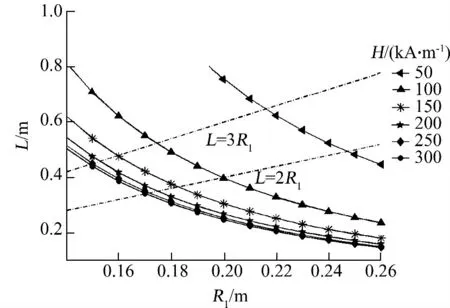
图6 不同磁场强度下联轴器提供额定转矩的尺寸Fig.6 Dimensions of MRF couplings at different magnetic field strength

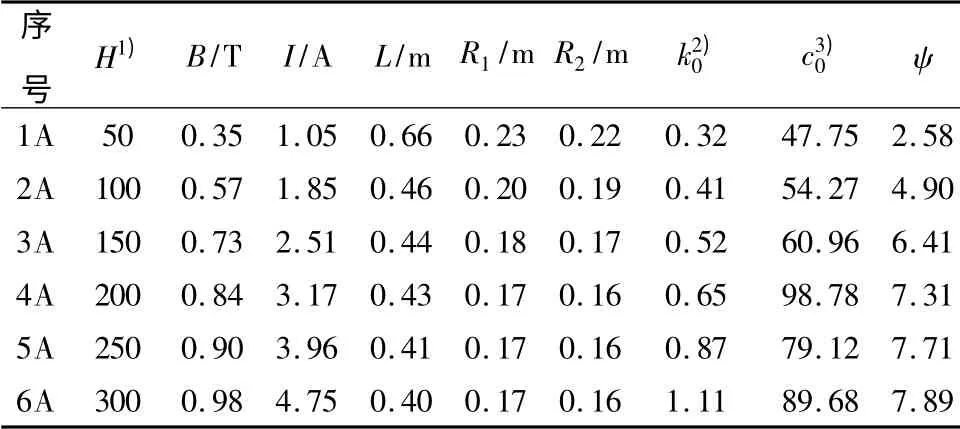
表1 磁流变液联轴器最优化设计参数(A 组)Table 1 Optimized design parameters of MRF couplings by example A

图7 不同励磁电流下的联轴器特性参数Fig.7 Properties of MRF couplings at different magnetization currents

图7 拟合了磁场强度、可调倍数和联轴器尺寸参数与电流之间的关系，统计确定系数R2分别为0.996、0.994 和0.994.由图7(a)和7(b)可以看到，当励磁电流增大时，磁场强度、可调倍数均增加，且当电流I ＞4A 时，增幅减小，相应变量达到稳定值1T 和8 倍左右，磁场强度反应了联轴器的剪切能力，可调倍数反应了联轴器可传递扭矩的适用范围;在联轴器尺寸优化条件的限制下，励磁电流高于2.5A 后，尺寸参数L、R1稳定在确定值.

对比目前常用联轴器的尺寸(如HL6型弹性柱销联轴器公称转矩为3150 N·m，轴向和径向尺寸分别为0.344 m 和0.280 m［17］;TL10 型弹性套柱销联轴器公称转矩为2 000 N·m，轴向和径向尺寸分别为0.344 m和0.315 m［18］)，结合图7 可知，当励磁电流I ＞4 A时，依据理论设计的磁流变液联轴器尺寸约为常用联轴器的1.2 倍，实际工程运用中基本不会因尺寸因素而影响使用.

系统制动过程中，在满足传递额定扭矩的前提下得到联轴器的设计尺寸参数，如A 组中数据.磁流变液联轴器在此过程中的传动特性如图8 所示.由图8(a)中可以看到，尽管励磁电流约增加了3.5 倍，相应地磁场强度增加了5 倍，而联轴器制动所用时间并没有产生较大波动，均在1 ms 之内，满足工业生产中对反应时间的要求;随着电流强度的增加联轴器尺寸减小.图8(b)反映了制动过程中粘滞传动力矩的减小，侧面说明动态屈服应力产生的转矩在传递扭矩当中占有更大的比例，这从A 组4A-6A 的数据曲线相差很小上得到验证.

图8 基于A 组数据系统在制动过程中联轴器的传动特性Fig.8 Transmission properties of MRF couplings during braking of system based on data group A

4.2 系统传递特性分析

在已知的结构优化设计数据基础上，易知若联轴器外形尺寸采用iA 组数据，则在其上施加jA 组中的电流强度(j≥i)均能满足传递额定力矩的要求.为了方便讨论该联轴器的传递特性，不妨取1A组几何参数和A 组1 -6 的电流强度数据，其组合得到一组新的设计参数(B 组)，如表2 所示.文中还给出了联轴器粘滞力矩和最大传递力矩的运动学特性曲线，如图9 所示.

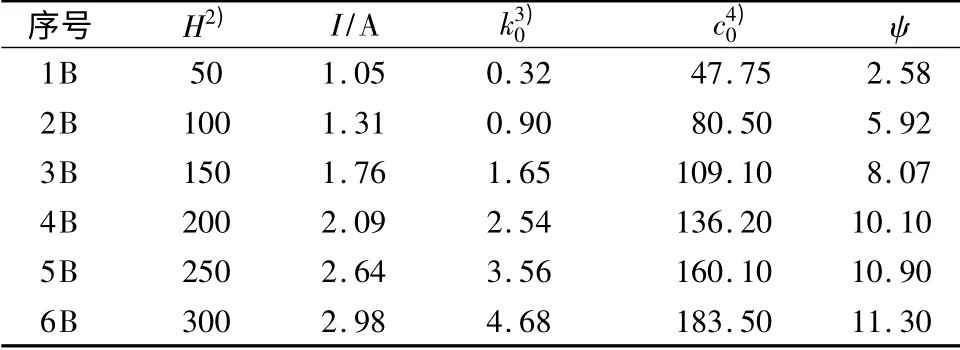
表2 磁流变液联轴器外形尺寸固定后的设计参数(B 组)1)Table 2 Optimized design parameters of MRF couplings with fixation dimensions by example B

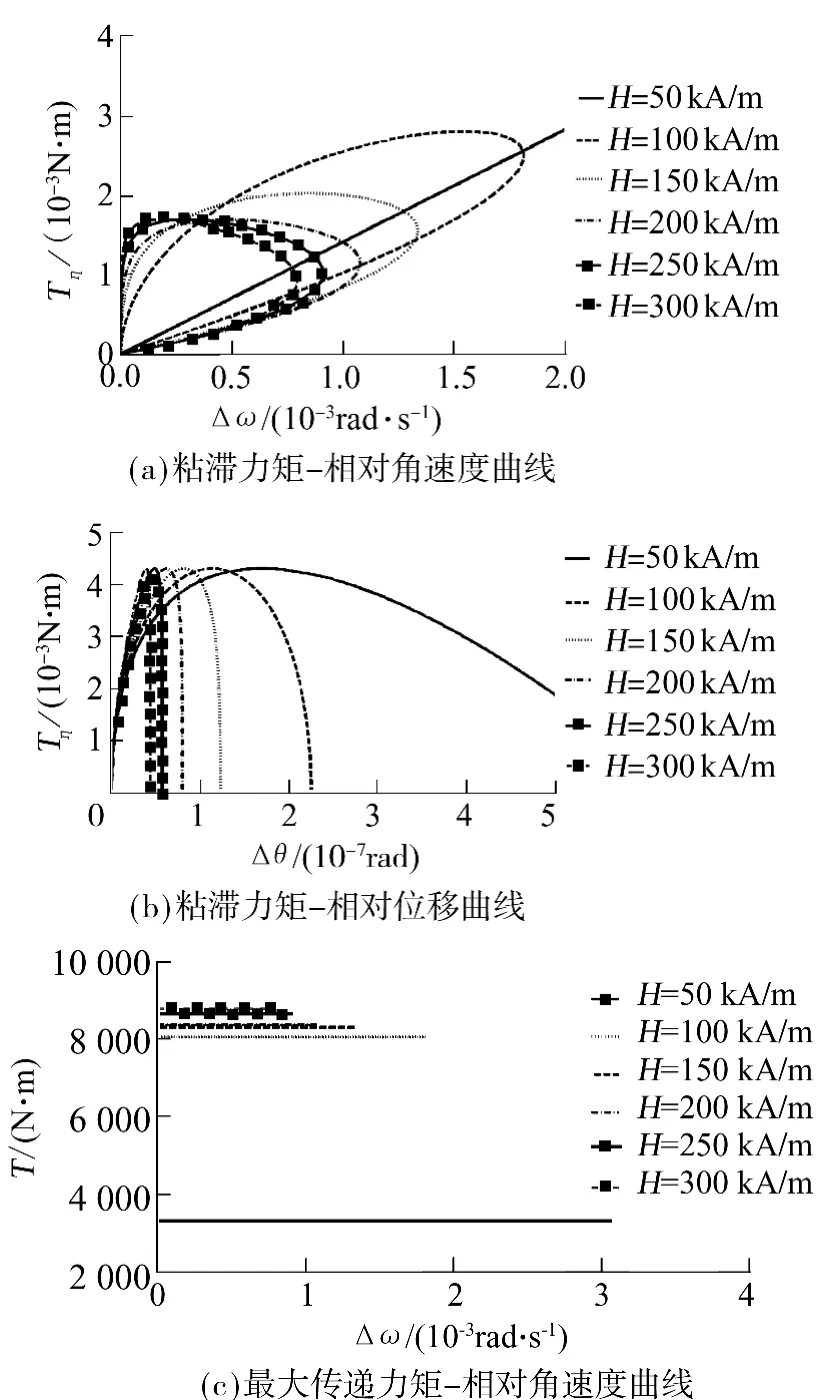
图9 联轴器粘滞力矩和最大传递力矩的运动学特性Fig.9 Dynamic properties of viscous torques and maximum transmission torques of couplings

对比图8(a)和图9(c)可以看到:确定联轴器尺寸后，增加电流强度能够获得更大的稳定传递力矩，随励磁电流的增大力矩作用在减弱;系统在此过程中最大相对角速度在减小，即更大的电流强度使得此过程更加稳定，反映在图9(a)和图9(b)粘滞力-运动学关系曲线上，曲线与坐标轴所围区域逐渐减小直至为0，等效转化成刚性联接，此时所传递的力矩与运动学参数无关.

基于A、B 这两组数据可得到联轴器的可调倍数随电流强度的变化，如图10 所示.从A 组数据可以看出联轴器尺寸数据对可调倍数的影响:对于尺寸确定的联轴器，当电流小于某一确定值(如3A)时，采用增加电流的方法可调倍数可获得明显的提高，当电流增加至3A 后，可调倍数的增加幅度减缓直至某一固定值.

图10 制动过程中磁流变液联轴器的可调倍数特性Fig. 10 Properties of adjustable multiple during braking of system

对于尺寸确定的联轴器，系统完成制动过程所用的时间显然与励磁电流强度呈负相关，且在励磁电流高于2.5A 后时间趋于稳定，如图11 中所示，其中t1为系统达到完全制动的稳定时间;与可调倍数类似，对比相同大小励磁电流下的稳定时间发现，联轴器尺寸数据亦对制动时间有不小的影响.

图11 制动过程中的稳定时间特性Fig.11 Properties of stabilization time during braking of system

由于系统起动过程的传动特性在数学表达式上与制动过程相似，可结合上述过程参考式(12)、(13)进行分析.

5 结论

文中研究了筒式磁流变液联轴器结构，进行了理论分析并获得了最大传递扭矩、相位转差和扭矩可调倍数等多个联轴器性能指标参数的显性解析式，为联轴器尺寸设计和系统运动分析建立机理模型.该机理模型避免了繁琐的数值求解和实验性能参数拟合曲线，具有更明确的物理意义，对类似结构磁流变液联轴器设计和特性分析具有更直接的指导和借鉴意义.文中的联轴器主要外形尺寸(φ0.34 m×0.4 m)与市场上同等额定参数的联轴器装置(如柱销联轴器)相比约为其尺寸的1.2 倍;通过理论数据分析联轴器关键的性能特征解，发现系统制动过程的稳定时间在1 ms 之内，传递扭矩可调倍数为3 ～10，其他参数如稳定传递力矩等满足工程实际应用中的要求.

［1］鲁光涛，李友荣，宋钢兵.工作间隙对磁流变液联轴器的影响［J］.功能材料，2013，44(1):71-75.Lu Guang-tao，Li You-rong，Song Gang-bing. Influence of working gap on magneto-rheological coupler ［J］. Functions and Materials，2013，44(1):71-75.

［2］Wang D H，Liao W H.Modeling and control of magnetorheological fluid dampers using neural networks ［J］.Smart Materials and Structures，2005，14(1):111-126.

［3］韩晓明，薄玉成，张鹏军，等. 车用磁流变离合器磁路设计研究［J］.机械设计与制造，2013，1(1):35-37.Han Xiao-ming，Bo Yu-cheng，Zhang Peng-jun，et. al. The design research about vehicle MR clutch magnetic circuit［J］.Machinery Design ＆ Manufacture，2013，1(1):35-37.

［4］申玉良，潘存治，杨绍普，等. 磁流变液离合器的设计与探讨［J］.机械设计，2005，22(6):21-24.Shen Yu-liang，Pan Cun-zhi，Yang Shao-pu，et al. Design and discussion on magnetic rheologic fluid clutch ［J］.Journal of Machine Design，2005，22(6):21-24.

［5］Wang X，Gordaninejad F. Flow analysis and modeling of field-controllable，electro-and magneto-rheological fluid dampers ［J］. Journal of Applied Mechanics，2007，74(1):13.

［6］Wang X，Wang D. Calculation of eddy current loss and thermal analysis for adjustable permanent magnetic coupler［J］. Electronic and Mechanical Engineering and Information Technology，2011，9(1):4405-4408.

［7］Imaduddin F，Mazlan S A，Zamzuri H.A design and modelling review of rotary magnetorheological damper［J］.Materials ＆ Design，2013，51(4):575-591.

［8］李宏男，杨浩，李秀贤.磁流变阻尼器参数化动力学模型研究进展［J］. 大连理工大学学报，2004，44(4):616-624.Li Hong-nan，Yang Hao，Li Xiu-xian.Adances of research on parameterized dynamic models of magnetorheolgical dampers［J］.Journal of Dalian University of Technology，2004，44(4):616-624.

［9］Hoang N，Zhang N，Du H.A dynamic absorber with a soft magnetorheological elastomer for powertrain vibration suppression ［J］. Smart Materials and Structures，2009，18(7):074009.

［10］瞿伟廉.磁流变液智能材料与器件及结构振动的智能控制［M］.北京:科学出版社，2013:31.

［11］周云，谭平.磁流变阻尼控制理论与技术［M］.北京:科学出版社，2007:26-27.

［12］Hong S R，Wereley N M，Choi Y T.Analytical and experimental validation of a nondimensional Bingham model for mixed-mode magnetorheological dampers［J］. Journal of Sound and Vibration，2008，312(3):399-417.

［13］Esteki K，Bagchi A，Sedaghati R. Dynamic analysis of electro-and magneto-rheological fluid dampers using duct flow models［J］. Smart Materials and Structures，2014，23(3):035016.

［14］Hoang N，Zhang N，Du H.An adaptive tunable vibration absorber using a new magnetorheological elastomer for vehicular powertrain transient vibration reduction ［J］.Smart Materials and Structures，2011，20(1):15-19.

［15］Li W H，Du H.Design and experimental evaluation of a magnetorheological brake［J］. Advanced Manufacturing Technology，2003，21(7):508-515.

［16］Lord Corp. MRF-132 DG magneto-rheological fluid［EB/OL］.(2014-05-23)［2015-03-27］.http:∥www.lord.com/products-and-solutions/magneto-rheological-(mr)/product.xml/1645/2.html.

［17］GB/T5014—2003，弹性柱销联轴器［S］. 北京:中国标准出版社，2013.

［18］GB/T4323—2002，弹性套柱销联轴器［S］. 北京:中国标准出版社，2013.