基于SMOTE采样和支持向量机的不平衡数据分类

曹路，王鹏



基于SMOTE采样和支持向量机的不平衡数据分类

曹路，王鹏

（五邑大学 信息工程学院，广东 江门 529020）

不平衡数据集广泛存在，对其的有效识别往往是分类的重点，但传统的支持向量机在不平衡数据集上的分类效果不佳. 本文提出将数据采样方法与SVM结合，先对原始数据中的少类样本进行SMOTE采样，再使用SVM进行分类. 人工数据集和UCI数据集的实验均表明，使用SMOTE采样以后，SVM的分类性能得到了提升.

不平衡数据；支持向量机；SMOTE；ROC曲线

现实生活中，不平衡数据集广泛存在，如：癌症诊断、信用卡欺诈等，其中，不平衡数据集中少类样本的识别往往才是分类的重点. 在医疗诊断中，如果把一个病人误诊为正常，可能会造成严重的后果；在信用卡欺诈检测中，如果将欺诈判断为正常事件，可能带来巨大的经济损失. 传统的分类器，如支持向量机（Support Vector Machine，SVM）[1]、决策树、神经网络等均是从优化整个数据集的性能出发而设计的学习机器，对多数样本类有较高的识别率，而对少数类的识别率却很低. 因此，传统的分类方法在处理不平衡数据集时存在弊端.

为了解决不平衡数据的分类问题，研究人员主要从算法层面和数据层面来改善分类性能[2]. 算法层面主要是对现有算法的改进和提升[3-4]，数据层面主要是通过重采样的技术来改善数据集的不平衡率，方法包括下采样和上采样. 下采样技术通过减少多数类样本来提高少数类样本的比例，但易因丢失多数类样本的信息而导致分类器无法正确学习[5]. 随机上采样通过随机复制少数类样本来达到增加少数类样本的目的，但新增加的数据有额外的计算代价[6]. 鉴于此，本文提出了一种基于SMOTE（synthetic minority over-sampling technique）[7]采样和支持向量机的不平衡数据分类，先对原始数据中的少类样本进行SMOTE采样，再使用SVM进行分类，以期提升分类器的分类性能.

1 基于SMOTE采样的SVM分类器的设计

1.1 不平衡数据对SVM算法分类性能的影响

为了测试数据不平衡对SVM分类器的影响，对两类符合正态分布的人工数据样本分别以不同的抽样比例生成训练集，再用SVM对它们进行分类. 其中一类样本中心为，另一类样本中心为，方差为（0.5,0;0,0.5）. 图1中，两类样本的比例分别为1000:1000，1000:200，1000:100，1000:10；蓝颜色的点代表正类样本，黑颜色的“+”代表负类样本，红线代表使用支持向量机分类后得到的分类面. 如图1所示，当采样比例不断向右上方的多类样本（蓝色样本)倾斜时，红色的分界线逐渐向左下方移动，越来越多的少类样本被错划为多类样本，导致少类样本的分类准确率下降. 这是由于训练样本数量不平衡所引起的. 在现实生活中，少数样本的错分代价远高于多数样本. 所以为了提高分类器的性能，需要解决分类的决策面偏向少类样本的问题.

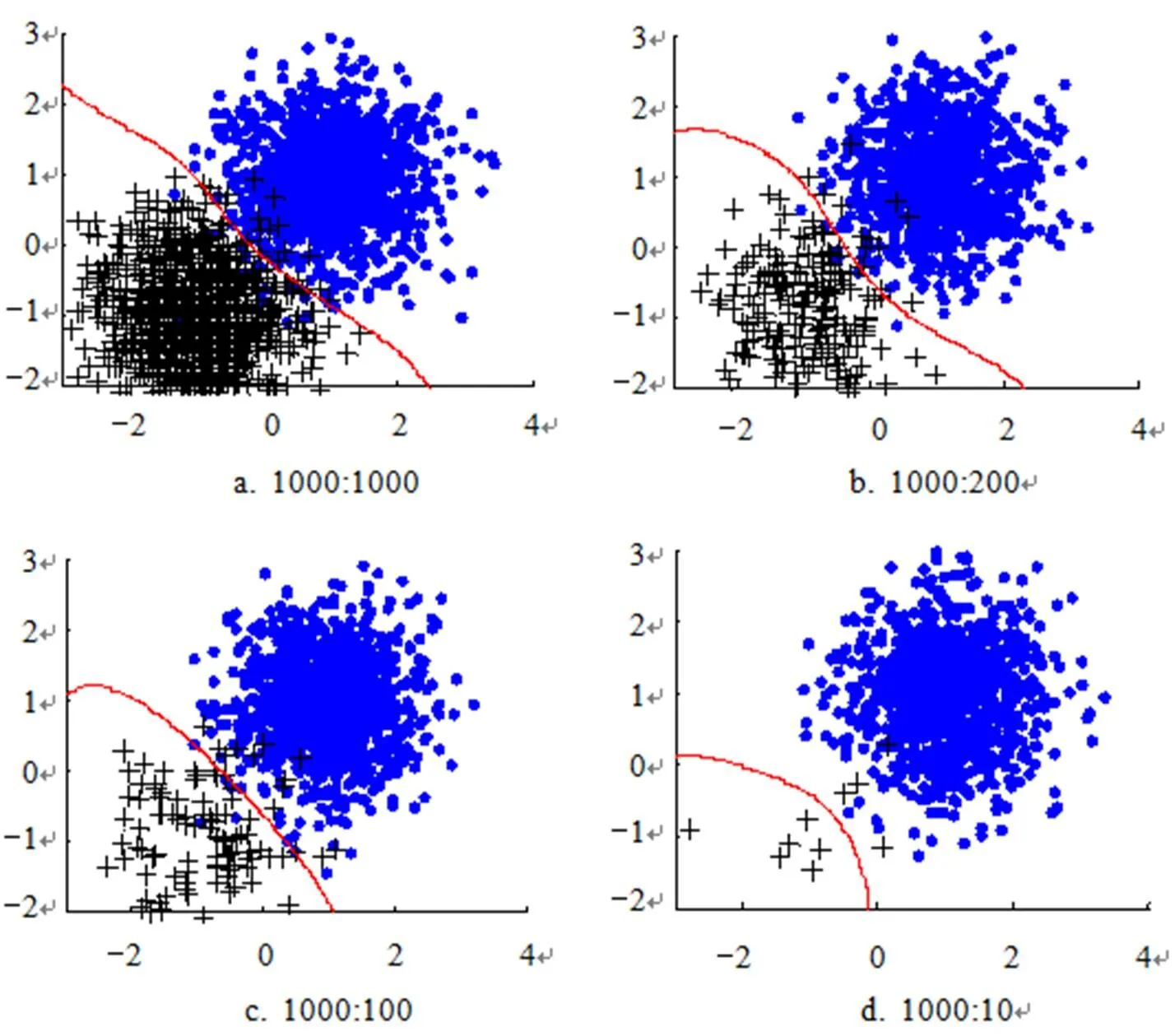
图1 两类样本不同比例下的分类面

1.2 SMOTE采样与SVM分类的结合

SMOTE方法是由Chawla等提出来的一种对数据过采样的方法，其主要思想是在相距较近的少数类样本之间进行线性插值产生新的少数类样本，降低两类样本数量上的不平衡率，提高少数类样本的分类精度. 其具体方法可概括为：对少数类的样本，搜索其个最近邻样本，在其个最近邻样本中随机选择个样本（记为），在少数类样本与之间进行随机插值，构造如式（1）所示的新的小类样本:

如图2所示，原始数据样本满足二元高斯分布，形状为方块；按照的比例对原始样本进行SMOTE采样，圆圈型样本是SMOTE采样之后的样本.

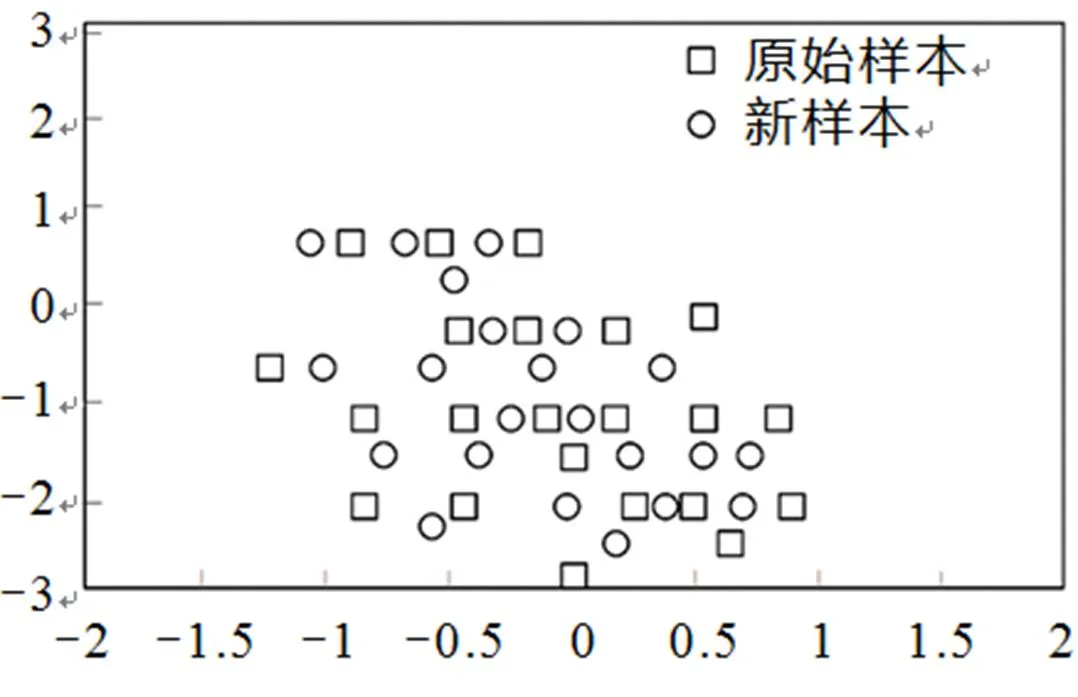
图2 SMOTE方法效果图

为了更好地对不平衡数据进行分类，本文提出将数据采样方法与SVM结合，先对原始数据中的少类样本进行SMOTE采样，再使用SVM进行分类，算法的流程图如图3所示. 具体步骤如下：

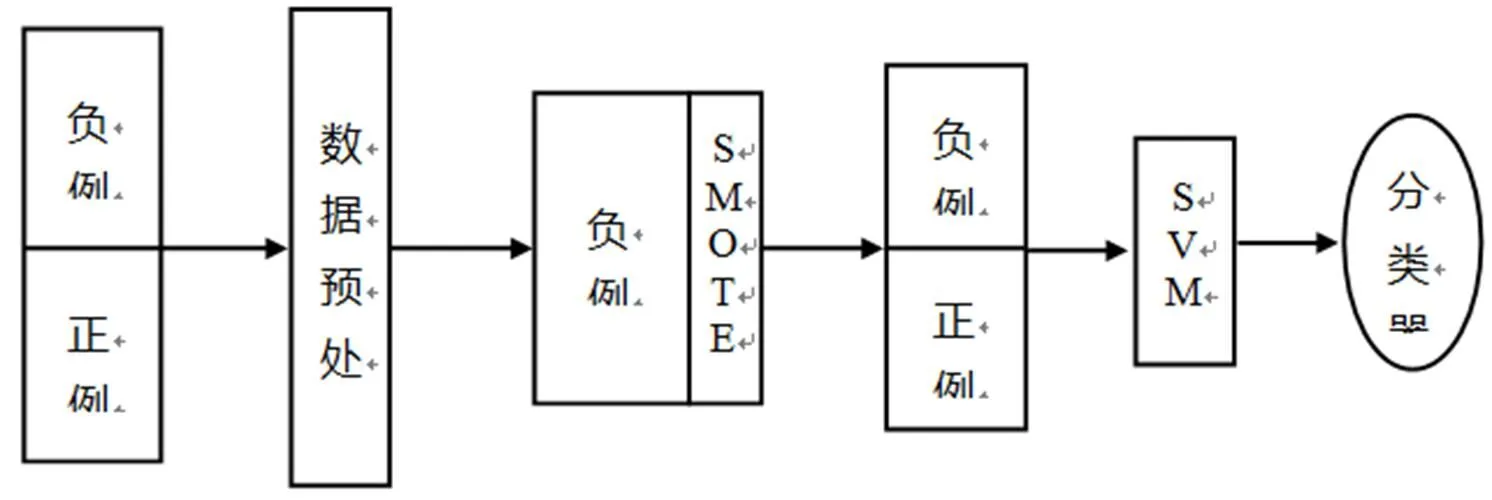
图3 基于支持向量机的采样方法流程图

1）对样本数据进行预处理. 本文的数据预处理是对数据集数据进行归一化处理，按照数据集的各自维数，把所有的数据都归一化为[0,1]之间的数，以消除各个不同维数的数据间的数量级差别，避免因输入数据数量级差别较大而产生的较大误差；

2）用SMOTE对负类样本采样，以降低多数类和少数类的不平衡程度；

3）用支持向量机进行学习，建立最终的分类器.

2 实验及结果分析

2.1 人工数据集

实验中的人造样本服从二维标准正态分布，其中一类样本中心为（1,1），另一类样本中心为，方差为（0.5,0;0,0.5），因此最优的分类面应该是一条通过原点的分界线. 分别选取了10个和100个作为少类样本和多类样本. 如图4所示，红色圆点表示多类样本，蓝色“+”点代表少类样本，蓝色线条是原始最佳分界面，红色线条是经过分类器之后建立的分界面. 很显然，SMOTE采样后的分界面明显优于原始不平衡数据的分类面. 本次实验在SVM建模的参数寻优过程中选取的是线性核函数，因此分类界面是直线.

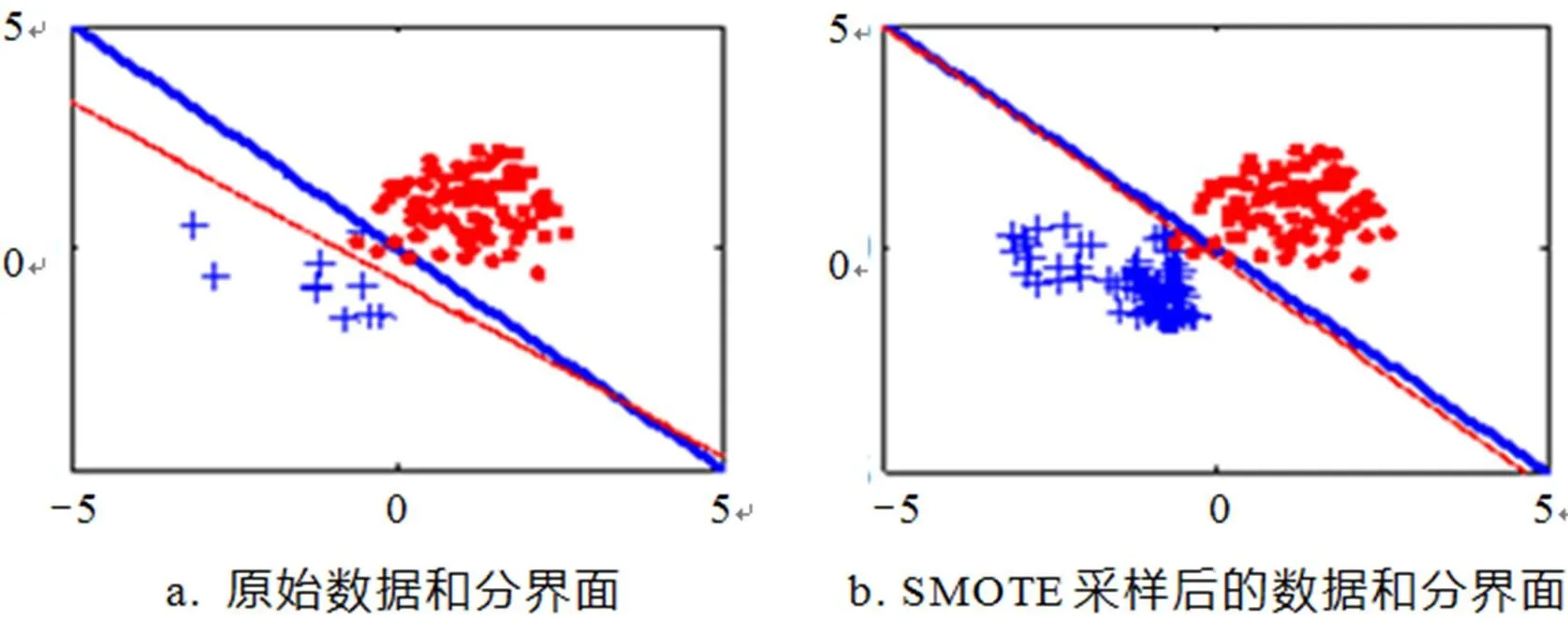
图4 人工数据集的样本分类

2.2 UCI数据集

本文选取5个不同平衡程度、不同样本数量的UCI数据集进行实验. 为了实验简便，可把多类数据集转化为两类. 对于类数较多的数据集，设定其中一类为少数类，剩余的合并为多数类. 数据集的总体描述如表1所示.

表1 数据集

传统的分类学习方法一般采用分类精度来评价分类的效果. 但对于不平衡数据，用分类精度来衡量分类器的性能是不合理的. 因为当少数类比例非常低时，即使将全部少类都分为多类，其精度仍然非常高，而这样的分类器是没有意义的. 目前，不平衡问题分类的评价标准有F-value、G-mean、ROC曲线等，它们都是建立在混淆矩阵的基础上的. 其中，ROC曲线能全面描述分类器的性能，已经成为不平衡数据分类性能评价的准则. 一般说来，ROC曲线越偏向左上角，分类器的性能越好. 由于ROC曲线不能定量地对分类器的性能进行评估，一般用ROC曲线下的面积（Area Under ROC Curve，AUC）来评估分类器的性能.

在实验的过程中，采用交叉验证的方法，将数据集中的样本随机分为5份：其中的4份作为训练集，剩下的1份作为测试集. 由于实验中所用到的采样方法都属于随机算法，为避免偶然性，本文将每种方法都独立执行5次，最后取5次AUC值的平均值作为该算法在整个数据集中的AUC值. 图5为不同数据集下的ROC曲线，由图可见，除了图5-e中Breast cancer数据集SMOTE采样前和SMOTE采样后ROC曲线接近外，其他数据集中采用SMOTE采样后的ROC曲线均更偏向左上角，说明采用SMOTE采样后，SVM的分类性能要优于原始数据集下的分类性能.

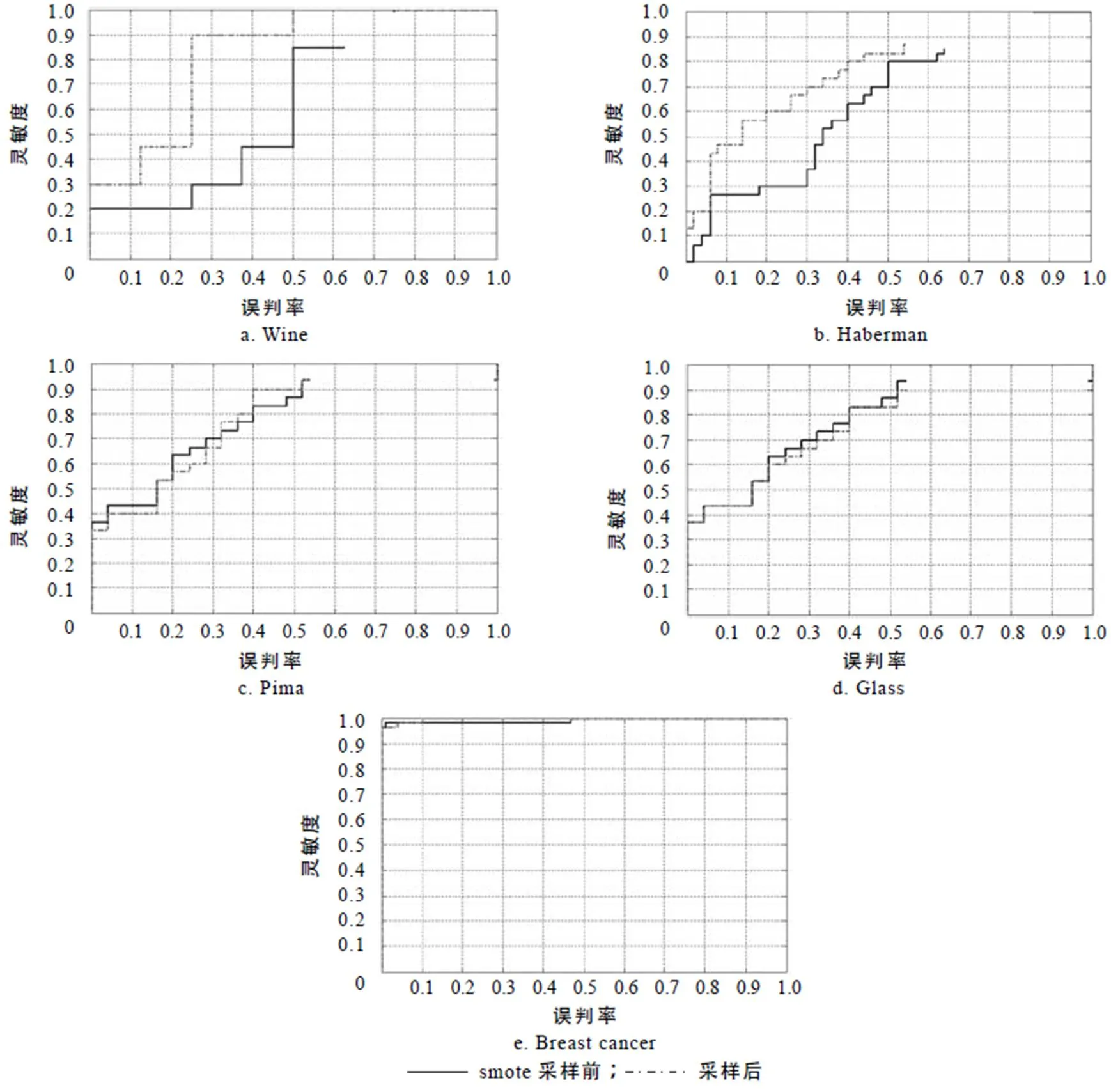
图5 不同数据集的ROC曲线

5组数据集在两种方法下所记录的AUC的平均值和分类精度平均值如表2所示. 由表2可知，相较于SVM分类算法，SVM+SMOTE算法除了在Breast cancer数据集上的AUC略低外，在其他数据集上均有不同程度的提升. 5个数据集的分类精度平均值亦有相似的实验结果，即除了Breast cancer数据集，经过SMOTE采样后，Wine、Haberman、Pima、Glass等4个数据集的分类精度平均值均得到了不同程度的提高. 这些说明采用SVM+SMOTE的方法能提高不平衡数据集的分类性能.

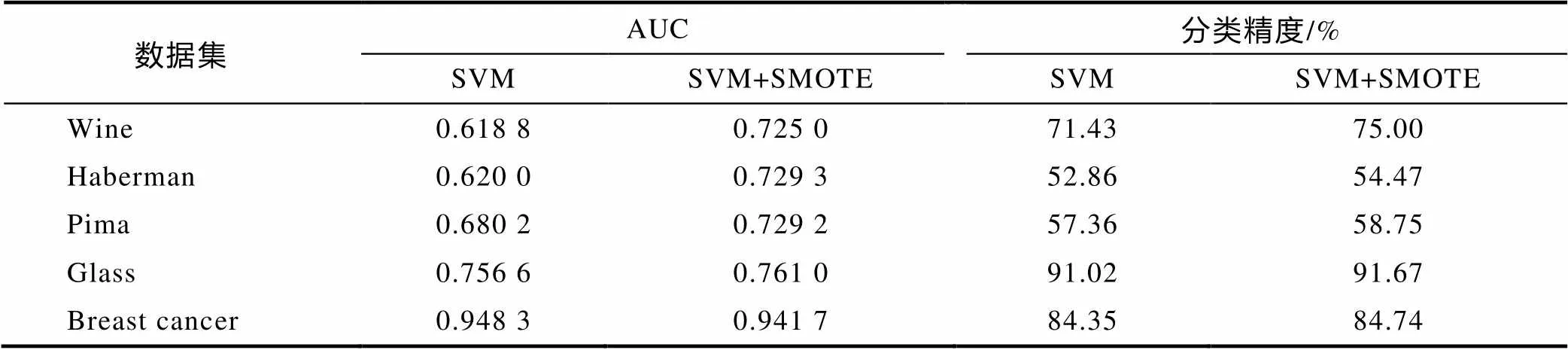
表2 5种数据集在两种方法下的AUC和分类精度的平均值

3 结论

传统的分类器对不平衡数据集中少数类样本的识别率较低，本文在讨论了不平衡数据对SVM算法分类性能影响的基础上，提出了一种基于SMOTE采样的SVM方法. 该方法首先对原始数据进行预处理，然后对少类样本进行SMOTE采样，最后再使用SVM进行分类. 实验结果表明，本文所提出的方法在少数类识别率和整体的分类精度上均优于传统的SVM算法，证明该算法是可行的、有效的. 如何利用上采样和下采样结合的方法，或者利用其他算法来提高不平衡数据集的分类性能是今后需要进一步研究的问题.

[1] VAPNIK V N. 统计学习理论[M]. 许建华，张学工，译. 北京：电子工业出版社，2004.

[2] 杨明，尹军梅，吉根林. 不平衡数据分类方法综述[J]. 南京师范大学学报（工程技术版），2008, 4(8): 7-12.

[3] 李秋洁，茅耀斌，王执铨. 基于Boosting的不平衡数据分类算法研究[J]. 计算机科学，2011, 38(12): 224-228.

[4] 王超学，张涛，马春森. 基于聚类权重分阶段的SVM解不平衡数据集分类[J]. 计算机工程与应用，2014, 25(4): 1-6.

[5] ESTABROOKS A, JO T. A multiple re-sampling method for learning from imbalanced data sets [J]. Computational Intelligence, 2004, 20(11): 18-36.

[6] AKBAR I R, KWEK S, JAPKOW I. Applying support vector machines to imbalanced datasets [C]//Proc of the 15th European Conference on Machines Learning. Berlin Heidelberg: Springer, 2004: 39-50.

[7] CHAWLA N, BOWYER K, HALL L, et al. SMOTE: Synthetic minority over-sampling technique [J]. Journal of Artificial Intelligence Research, 2002, 16: 321-357.

[8] 陶新民，郝思媛，张冬雪，等. 基于样本特性欠取样的不均衡支持向量机[J]. 控制与决策，2013, 28(7): 978-984.

[9] 邓乃扬，田英杰. 支持向量机——理论、算法与拓展[M]. 北京：科学出版社，2009.

[10] WANG Quan, CHEN Weijie. A combined SMOTE and cost-sensitive twin support vector for imbalanced classification [J]. Journal of computational information systems, 2014, 12(10): 5245-5253.

[责任编辑：熊玉涛]

Imbalanced Data Classification Based on SMOTE Sampling and the Support Vector Machine

CAOLu, WANGPeng

(School of Information Engineering, Wuyi University, Jiangmen 529020, China)

Imbalanced data sets exist widely in real life and their effective identification tends to be the focus of classification. However, the results of classification of imbalanced data sets by traditional support vector machines are poor. This paper proposes combining data sampling and SVM, conducting SMOTE sampling of minority samples in the original data and then classifying them by SVM. Experiments using artificial datasets and UCI datasets show that by adopting SMOTE sampling, the performance of classification by SVM is improved.

imbalanced data; support vector machines; SMOTE; ROC curve

1006-7302（2015）04-0027-05

TP273

A

2015-07-17

2013年五邑大学青年基金资助项目（2013zk07）；2014年五邑大学青年基金资助项目（2014zk10）；2015年江门市科技计划项目（201501003001556）

曹路（1983—），女，湖北松滋人，讲师，硕士，研究方向为模式识别.