一种基于Arnold变换和RSA的图像加密算法
2015-10-20邓家先邓海涛
曹 静,邓家先,邓海涛
(海南大学信息科学技术学院,海南海口570228)
随着Internet技术的飞速发展,人们可以利用网络传输大量的文本、多媒体、数字图像、视频等,相应的信息安全和保密性问题也日益凸显。于此同时,加密秘钥的管理问题和分发问题随之产生。传统的加密技术主要针对内容性数据,但对图像、声音等相邻像素高度相关和冗余的具有一定结构数据的加密方法还在寻找当中[1]。很多文献提出了可行有效的图像加密算法[2-7]。Shannon 指出,扩散[8]能够能把明文的冗余信息分散到密文中,使得明文不再具有统计结构,而置乱是实现扩散的主要方法。
混沌系统具有类随机性,利用其产生密钥序列是近年来新发展的一种加密技术。混沌信号具有对初始条件的极端敏感性,各态历经性、非周期宽频谱性,因而用这种方法加密的信息很难破译,具有很高的保密度。Fridrich于1997年提出[9]将混沌系统应用于图像加密,使用二维的Baker映射和Arnold变换对图像的像素点的位置进行变换,其变换实质是通过改变像素点的位置来扰乱图像相邻像素间的相互关联程度,图像灰度并未改变[10],因此置乱的安全性极低。
公钥密码体制为密码学的发展提供了新的理论和技术基础,成功解决了密钥分发、密钥管理等问题,已成为信息安全领域中的核心技术。当前最流行的[11]RSA算法是一个较为完善的公开密钥算法,其非常容易理解和实现。该加密算法已经经受住了多年深入分析,具有一定的可信度。
综上考虑图像像素点位置、灰度值变化及秘钥分发管理问题,本文提出一种将数字图像数据置乱和RSA加密机制相结合的方法,实现图像加密。算法在以往Arnold连续迭代k次对图像像素位置置乱的基础上做了改进,用不同初值的Logistic混沌映射产生Arnold变换参数序列,使得每次置乱的Arnold矩阵都不同。同时利用RSA算法对置乱后的像素值采用密文链接模式的替代和扩散过程,使密文和明文相关,实现灰度值的改变。
1 Arnold变换原理
Arnold变换是在遍历理论的研究中引入的一种非线性映射,可以看作是裁剪和拼接的过程。猫映射没有吸引因子,是一个表面积映射[12-16],而且也是一个一一映射,单位矩阵内的每一个元素唯一地变化到位矩阵内另一个元素位置。它可对平面的坐标进行一种置乱变换,进而将其推广为
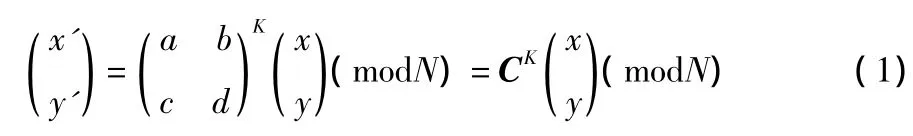
式中:x,y∈{0,1,2,…,N-1},N 为图像矩阵的阶数;(x,y)是原图像中像素点的坐标;(x',y')是变换后该像素点对应的坐标;k为迭代次数;a,b,c,d是满足 ad-bc=1时的任意正整数。图1是Arnold映射的示意图,可看出该映射具有拉伸和折叠特性,这种性质使得置乱有一定程度的初值敏感性[17]。
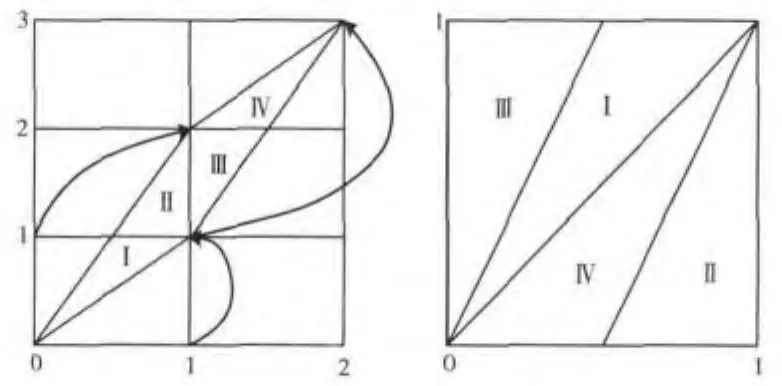
图1 猫映射的拉伸和折叠原理
Arnold变换具有周期性,经过反复迭代,就能恢复原图像,这种利用其周期性来恢复原图的方法耗时长。田云凯等提出,若原图像通过k步Arnold变换到达某一置乱状态,则需要用该算法迭代同样的步数来便捷地恢复原图像,无需计算其周期,大大节省了复原时间[18]。根据式(1),可以方便地给出猫映射的逆映射为
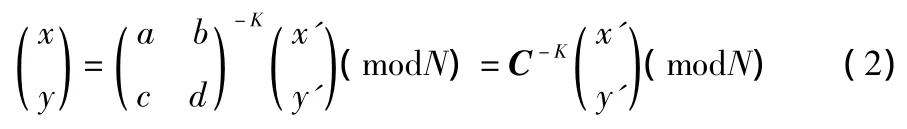
当已知猫映射混沌序列中任意一组(x,y)的值时,把加密了的图像按逆映射迭代相同的次数就可以解密,整个计算过程简单且效率很高。
2 RSA加密体制
RSA体制是基于陷门单向函数的概念,其安全性基于大数分解。大素数的产生是RSA公开密钥体制中最重要的步骤。
2.1 RSA算法描述
步骤1:选取两个随机大素数p和q;
步骤2:计算模 n=pq,φ(n)=(p-1)(q-1),φ(n)是 n 的欧拉函数;
步骤3:随机选择整数 e(1<e<φ(n)),满足 gcd(e,φ(n))=1,即 e与 φ(n)互素;
步骤4:用扩展Euclid算法算出私钥d,以满足d×e=1(modφ(n)),公钥为(e,n),私钥为(d,n);
步骤5:每次发送的明文m的长度为l(l<lb n),并通过c=me(mod n)进行加密;
步骤6:信息接收者用自己保存的私钥 d,通过 m=cd(mod n)进行解密。
2.2 常用素数的生成算法介绍
2.2.1 传统的筛选算法
选择一个随机数n,若n为合数,则可分解成n1×n2,n1和n2必有一个因数小于,则用n除以小于的所有素数,都除不尽则n为素数,否则n为合数,需要重新生成随机数n。
2.2.2 Rabin-Miller测试法
Rabin-Miller是一个很容易实现且被广泛使用的算法,其运算速度快,通过该测试后被测数为素数的概率更高,通过t次测试后,被测数是合数的可能性不超过1/4t。
首先,选择一个待加密的随机数p,计算b,b是2整除p-1的次数(即2b能整除p-1最大幂数),然后计算m,使得n=1+2bm,此算法的基本思想如下:
步骤1,选择一个小于p的随机数a,设j=0,z=ammod p。
步骤2,若z=1或 z=p-1,那么 p通过了测试,可能是素数。
步骤3,若j>0且z=1,那么p不是素数。
步骤 4,设 j=j+1,若 j< b 且 z≠p-1,设,z=z2mod p,返回到步骤3;若z=p-1,那么p通过测试,可能是素数。
步骤5,若j=b且z≠p-1,那么p不是素数。
3 算法的设计与实现
本文首先利用Arnold变换对图像的像素位置进行循环迭代置乱,再利用RSA公钥对像素值进行替代和扩散,完成加密过程,其流程图如图2所示。
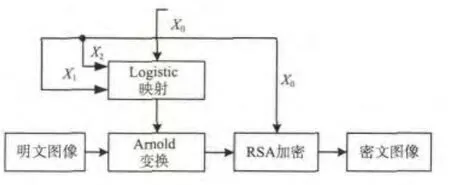
图2 加密流程
3.1 像素位置置乱
采用密钥扩展算法将变化的Logistic映射的密钥种子(x,λ)扩展成长度为20的序列,随机选取满足条件 ab-c=1 时的参数序列 a,b,c,使每次置乱的Arnold矩阵都不同,对图像像素位置进行3次循环迭代置乱。
设Logistic混沌系统的密钥种子:X0=0.365 645 710 269 86,λ0=3.965 2,产生参数 a=2,b=2,c=5,进行第一次位置置乱;xk=xk-1(1+10-14)产生参数a,b,c,进行第k次置乱。用此方法对图像像素位置进行置乱,很好地避免了Arnold的周期性,不用担心循环到某一次就会恢复到原图像,即Arnold变换的庞加莱性[19]。其解密就是根据每一次迭代的Arnold矩阵求出其逆映射矩阵,便可恢复到原来的像素位置。
3.2 像素灰度值的替代和扩散
生成一个 100 以内的小素数库 S={2,3,5,7,11,13,17,19,…},然后结合上述两种素数生成算法生成两个互素的大素数p和q。先利用传统的筛选算法排除其是合数的绝大多数可能性,以减少对随机生成的大整数进行测试的总次数,再利用Rabin-Miller测试法产生大素数。具体步骤如下:
步骤1:随机生成一个大整数p,若最低位为偶数,则其加1,以确保该素数为奇数;
步骤2:用传统的筛选算法检测一个随机数p是否为素数;
步骤3:对筛选出的p整除小素数库s里的素数,若都不能整除,则转到步骤4,否则跳转到步骤5;
步骤4:进行k次Rabin-Miller测试,若通过测试,则p是伪素数,否则跳转到步骤5;
步骤5:s+=(2步骤3中s自动加2),跳转到步骤3。
由生成的大素数p和q根据RSA算法原理计算出公钥PKB=(e,n),私钥 SKB=(d,n),为简便起见,本文取用较小的素数,p=241,q=193,n=p q=46 513,φ(n)=46 080,公钥e=41 677,得出解私钥d=9 733。然后利用RSA公钥对像素值进行扩散和替代过程。
初始值为
r0=(x0×1010)emod n (3)式中:x0为产生Arnold参数序列的Logistic混沌映射的初值。
采用密文链接模式将加密前的明文与前次的密文进行异或运算,再进行RSA加密,准备与下一个明文进行异或,使得密文与明文具有相关性。
密文链接模式的加密、解密过程如图3所示。
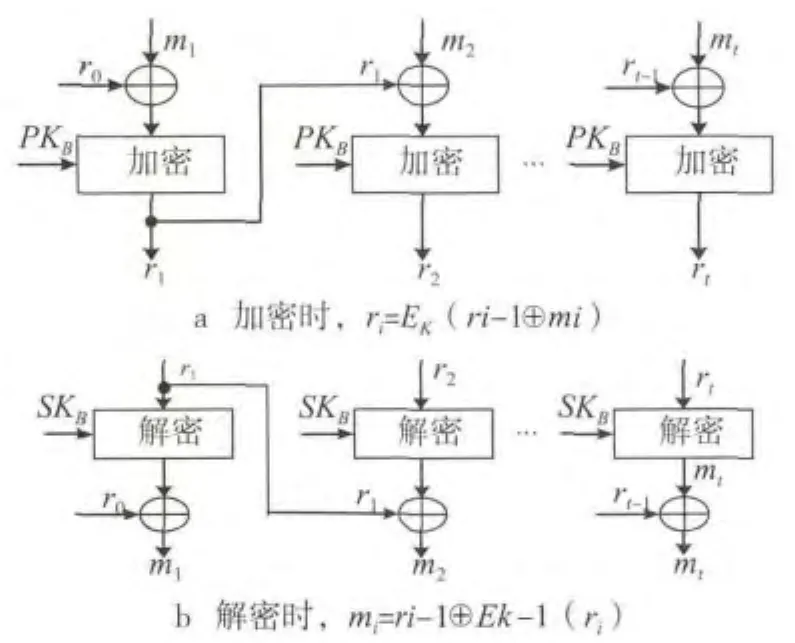
图3 密文链接模式的加密/解密过程
4 仿真结果及分析
本文采用Lena 512×512,灰度级为256的图像作为原始明文图像,选用Arnold变换对图像像素位置进行1次、3次置乱,得到图4b和图4c。从视觉系统[20]的角度来说,无法从置乱图像中观察出图像的原貌,置乱效果良好;然后采用公钥加密体制RSA对像素灰度级进行替代和扩散,最后完成加密过程,最终得到一幅非常混乱的密图4d,图像纹理细腻,颗粒均匀。图4e为RSA解密为猜测前一像素值加密错误,再进行解密的图像,图4f为正确解密图像。

图4 仿真结果
4.1 灰度直方图分析
灰度直方图表示数字图像每一灰度级与该灰度级出现频率的对应关系,是图像的重要统计特征[21]。图像的灰度密度函数与像素所在的位置有关,设图像在(x,y)的灰度分布密度函数为P(z;x;y),那么图像的灰度密度函数[14]为
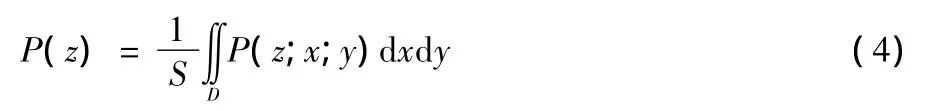
式中:D是图像的定义域;S是区域D的面积。
图5为明文图像及加密图像直方图。由5a可以看出,Lena图像的像素点集中分布在某些灰度级上,为非均匀分布;在加密后,如图5b所示,图像像素的灰度级出现的频率分布在整个灰度值空间,呈均匀分布,使明文图像的统计特性被完全打破,说明该加密算法使得灰度均匀分布,因此可以抵抗一定程度的统计分析攻击。
4.2 相邻像素相关性分析
图像相邻像素的相关性可反映图像置乱的程度,相关性越大,置乱效果越差,相关性越小,置乱的效果越好[22]。表1为 Lena、Airplane、Barbara、Boat、Baboon 几幅图像加密前后其水平、垂直和对角线3个方向的相邻像素之间的数据相关系数[23],其计算如下
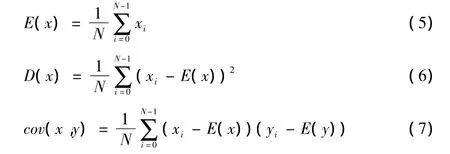
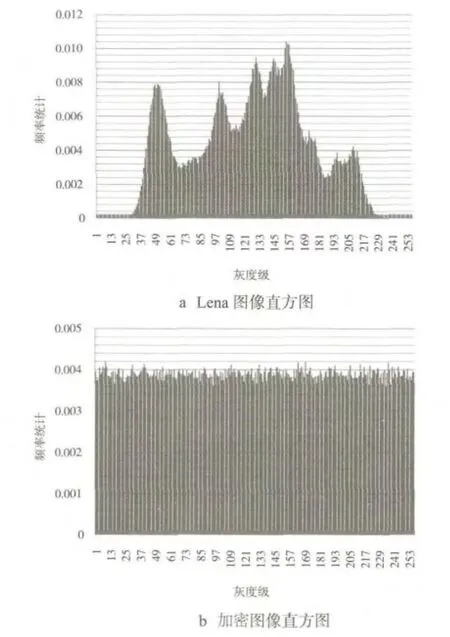
图5 加密前后图像直方图

式中:x,y为两个相邻像素值;N为像素数;E(x)是x的数学期望;D(x)是x的方差;rxy为两个相邻像素的相关系数。表2为对Lena图像1次Arnold置乱、3次Arnold置乱及最终RSA加密图像抽取水平、垂直和对角方向相邻像素对4 096对,利用式(5)~式(8)分别测试其相关系数,可知加密图像相较于原始图像在各方向的相关系数均小得多,Arnold多次置乱的效果非常明显;由加密前后相邻像素各方向相关性的散点图(图6),也可以看出,明文图像各方向像素间的相关性都近似于线性关系,说明明文图像像素间相关性很高;密文图像各方向像素间的相关性为随机分布,说明其相关性很低。因此,该算法去相关性强。
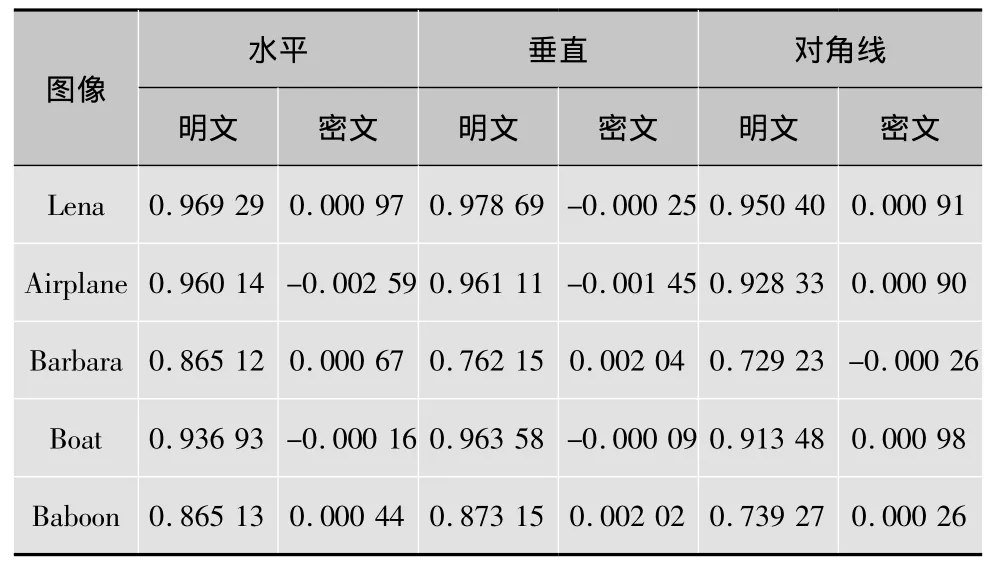
表1 图像加密前后相邻像素相关性
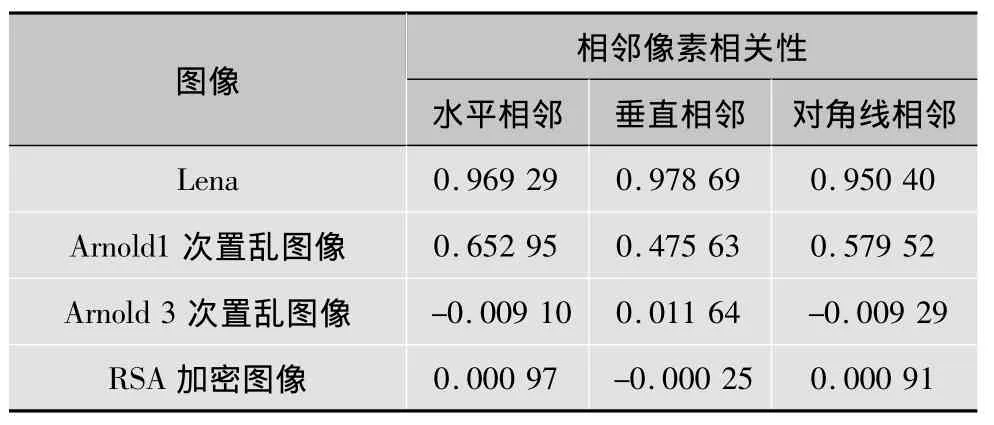
表2 Lena图像多重置乱前后相邻像素相关性
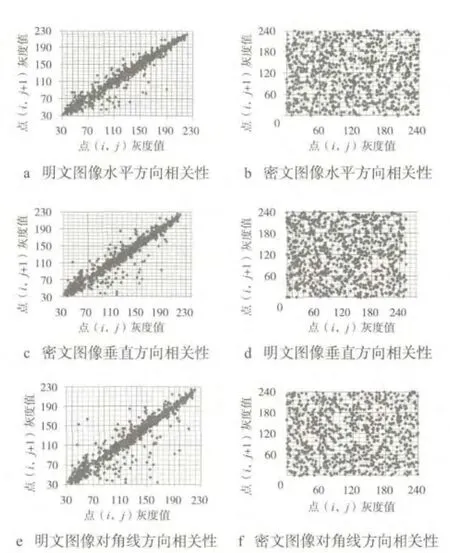
图6 加密前后相邻像素相关性
4.3 抗攻击性分析
利用Logistic混沌映射产生Arnold变换矩阵的参数(a,b,c)随着变化的密钥种子(x,λ)非线性映射Arnold变换循环迭代的参数改变,其加密的密钥空间增大,每迭代一次明文、密文、密钥间的关系具有高度非线性和复杂的统计关系;进一步对图像像素值进行了链接模式的替代与扩散,当中的取模运算也具有非常强的非线性。这使得要找到一个非常逼近的明文与密文线性关系几乎不可能,所以可以有效抵抗明文攻击。
由算法可知,像素值解密时要知道密钥初值和上一个像素值的加密过程,逐个将图像中像素点的灰度值解出。在已知加密算法是RSA的前提下,必须要知道相关的密钥r0,x0,(e,n)和(d,n),这又回归到大素数分解的问题,有相当大的难度。而且在正确恢复像素的位置时,解密要从后面开始进行Arnold的逆映射的迭代,前一步骤解密的正确与否影响到下一步骤的正确进行,每一轮迭代置乱的穷举密钥空间为(512×512)!,且加密时又采用变化的Logistic初值控制每次迭代的参数a,b,c,因此可以抵抗穷尽密钥搜索攻击。
5 结论
本文提出的算法实现了对图像像素位置的置乱和灰度值的扩散,达到了很好的加密效果。采用公钥加密体制同时也解决了密钥分发和密钥管理问题。整个加密过程具有很强的保密性、高度的非线性和复杂的统计关系,安全性高,软件实现简单,在图像加密领域有着广泛的应用前景。
[1]曹光辉,胡凯,佟维.基于Logistic均匀分布图像置乱方法[J].物理学报,2011,61(11):1-8.
[2]刘金梅,丘水生.混沌系统在密码学中的应用现状及展望[J].计算机工程与应用,2008,44(14):5-12.
[3]田园,邓鲁耀,张浩.几个通用公钥加密方案的匿名性条件[J].通信学报,2009,30(11A):8-16.
[4]贺楚雄,田绍槐.基于灰度级出现频数的数字图像置乱程度衡量方法[J].中国图象图形学报,2010,15(2):220-228.
[5]邓海涛,邓家先,邓小梅.一种基于EZW的ROI图像联合压缩加密算法[J].电视技术,2013,37(9):45-51.
[6]李晔,姜竞赛,樊燕红.一种混沌加密算法的改进[J].电视技术,2011,35(2):37-47.
[7]刘亮,吴怀宇.随机数列在数字图像加密中的应用[J].电视技术,2006,30(8):115-120.
[8]王育民.Shannon信息保密理论的新进展[J].电子学报,1998,26(7):27-34.
[9] XU SJ,WANG J,YANG S X.An improved image encryption algorithm based on chaotic maps[J].Chinese Physics B,2008,17(11):4027-4032.
[10]蔡邦荣.数字图像置乱评估方法研究[D].大连:大连理工大学,2011.
[11]谢元斌,史江,郝跃.一种长整数模乘幂的改进算法与实现[J].西安电子科技大学学报,2011,38(2):129-134.
[12] QI Dongxu,ZOU Jiancheng,HAN Xiaoyou.A new class of scrambling transformation and its application in the image information covering[J].Science in China(Series E),2000,43(3):304-312.
[13]郭琳琴,张新荣.基于二维Arnold变换的图像双置乱算法[J].计算机应用与软件,2010,27(4):264-266.
[14]张海涛,姚雪,陈虹宇.基于分层Arnold变换的置乱算法[J].计算机应用,2013,33(8):2240-2243.
[15]王圆妹,李涛.基于Arnold变换的高效率分块图像置乱算法的研究[J].电视技术,2012,36(3):17-19.
[16]陈善学,姚小凤,周淑贤.基于Arnold变换的改进方法[J].电视技术,2011,35(17):33-35.
[17]马在光,丘水生.基于广义猫映射的一种图像加密系统[J].通信学报,2003,24(2):51-57.
[18]田云凯,贾传荧,王庆武.基于Arnold变换的图像置乱及其恢复[J].大连海事大学学报,2006,32(4):107-109.
[19]任洪娥,尚振伟,张健.一种基于Arnold变换的数字图像加密算法[J].光学技术,2009,35(3):384-390.
[20]刘挺.一种基于HVS的空域分块数字水印技术[J].电子设计工程,2012,20(6):184-185.
[21]黄辉,任国强,孙健.基于图像直方图统计的CCD相机自动调光算法[J].半导体光电,2013,34(4):698-701.
[22]廖晓峰,肖迪,陈勇,等.混沌密码学原理及其应用[M].北京:科学出版社,2009.
[23]王静,蒋国平.一种超混沌图像加密算法的安全性分析及其改进[J].物理学报,2011,60(6):82-89.
