基于有理数多项式先验模型的图像盲去模糊

李 桐，胡绍海，刘帅奇，孙宇恒

（1.北京交通大学 信息科学研究所，北京 100044；2.河北大学 电子信息工程学院，河北 保定 071002）

在数码相机日益普及的今天，相机抖动或者物体运动造成的图像模糊现象严重影响了使用者对数码产品的体验，怎样从模糊图像中恢复出清晰图像成为了各国科学家研究的热点问题。模糊图像被复原成清晰图像属于图像复原，这一复原过程被称为图像去模糊。由于模糊核函数是未知的，故这种图像复原的过程称为模糊图像盲复原。图像去模糊技术在摄影、航空、航海、地质勘探等领域起着显著的作用。对单幅图像进行图像盲去模糊非常困难，由于只有一个已知量（模糊图像），而要求出两个未知量（清晰图像和模糊核），因此该过程是一个病态问题的求解过程。求解这样的问题通常是对模糊图像或者模糊核增加一些先验约束进行正则化求解。

Fergus[1]等人利用图像的先验知识和模糊核的约束条件对模糊图像进行正则化求解。通过大量自然图像的对比试验，提出清晰图像与模糊图像在图像的梯度分布上区别很大，清晰图像的梯度符合长拖尾分布，而模糊图像的梯度不符合这种特征。利用混合高斯函数作为约束函数对自然图像梯度分布进行拟合，并采用变分贝叶斯方法估计出模糊核，通过传统R-L算法恢复原始图像。由于图像梯度分布函数具有广泛性，因此该方法可以得到较好的去模糊效果。但是由于混合高斯函数拟合自然图像梯度分布时，在梯度值较大的地方往往会出现过拟合现象，从而导致去模糊后的图像产生了严重的振铃效应。

本文对Fergus算法进一步改进，采用有理数多项式拟合自然图像梯度分布。虽然与混合高斯函数相比，有理数多项式函数在拟合自然图像梯度特征时在误差项平方和（SSE）、确定系数（R-square）、校正的决定系数（Adjusted R-square）、均方根（RMSE）等拟合优度标准上只具有略微的优势，但是有理数多项式函数大大的削弱了拟合过程中的过拟合现象，从而使模糊核的估计更准确，减小了由此而带来的振铃效应，对模糊图像的复原更加有效。

1 模糊图像模型

运动模糊退化图像的数学模型一般为

式中：B为输入的模糊退化图像；K为模糊核；L为清晰图像；N为成像过程中加性噪声。

图像去模糊的目标就是求解清晰图像L。一般情况下，是在抑制噪声的情况下，先求解模糊核K，然后通过传统的反卷积算法求解得到清晰的图像L。设 p(L)是清晰图像的概率密度函数，p(B)是模糊图像的概率密度函数，而 p(L|B)表示已知模糊图像条件下，原始清晰图像的条件概率密度。根据贝叶斯定理，则有下式成立

由于模糊核K需要利用模糊图像B来估计，式（2）可以写成

在模糊图像B已知时，可以得到如下的关系

即可得

E(K)=-lg(p(K))，其中E(B|L,K)是图像噪声约束项，也是模糊图像B、清晰图像L和模糊核K之间的数据匹配约束项，E(L)是对自然图像的特征约束项，E(K)是对模糊核的特征约束，设E(L,K|B)为能量项，则有

由于上述模型已知量B的个数小于未知量L、K的个数，所以这是一个病态问题的求解过程，在理论上难以获得精确的解，因此通过L、K的大量迭代，在实验中能够获得最优解，EK(K)和EK(L)为能量项，对二者进行迭代即迭代以下两个能量

这样，把通过贝叶斯理论建立的求最大后验概率（MAP）问题[2]转化成求最小能量问题。计算迭代出模糊核，最后通过反卷积得到清晰图像。

2 有理数多项式函数拟合自然图像梯度分布特征函数

通常认为自然场景图像具有平滑性或者分块平滑性，通过图像的梯度可以体现图像的平滑性。图像的梯度值大部分情况下比较小，分布在梯度为零值附近，很少一部分会出现较大的值，这说明图像梯度是稀疏的。梯度值较大的部分，对应的是图像中的细节。以往论文都通常假定图像梯度的分布特征服从一个高斯模型，即

式中：‖ ‖

∀F 为图像梯度，利用图像梯度的分布约束能够减少图像去模糊过程中的不确定性，但是在假设中强制图像梯度分布服从高斯分布，导致模糊核估计不准确，恢复结果过于平滑，因此引入较强的振铃效应[2]。

实际上，自然场景图像梯度并不服从高斯分布，因此利用高斯模型进行图像去模糊的效果并不是很好。本文对图像先验约束模型进一步改进，提出用有理数多项式函数拟合自然图像梯度分布特征函数。大量图像分析统计发现，自然场景图像的梯度分布具有一个很明显的长拖尾曲线特征[3-4]。自然场景图像具有很强的平滑性，大部分梯度值都在零值附近，而图像梯度分布图中很长的拖尾是由梯度值较大的点造成的，对应的是自然场景图像中的细节。

图1是利用20幅自然图像统计的自然图像的梯度分布，其横坐标为梯度值，纵坐标为梯度值对应的概率的对数。

Fergus采用混合高斯函数拟合自然图像的梯度分布

式中：an，bn和cn为高斯函数参数。

图2即为混合高斯函数拟合的效果图，其中黑点为经过计算统计得到的图像真实概率密度，untitled fit 1为混合高斯拟合函数。可以看到在拟合过程中，混合高斯函数拟合在梯度为100～150时，出现比较严重的过拟合现象。

图1 自然图像的梯度分布

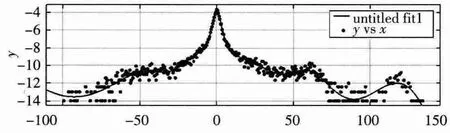
图2 混合高斯函数拟合自然图像梯度分布

为了防止过拟合现象的出现，本文采用有理数多项式函数拟合自然图像的梯度分布

在有理数多项式函数中，通过曲线拟合确定有理多项式中的系数 p和q。调节多项式的项数可以对拟合效果进行调整，但是考虑到项数多会产生冗余，增加了计算复杂度和计算时间，故本实验采用上述函数。

图3为有理数多项式函数拟合的效果图，其中黑点为图像的真实概率密度，untitled fit 2为有理数多项式函数拟合函数。可以看到该函数克服了拟合过程中出现的过拟合现象。

图3 有理数多项式函数拟合自然图像梯度分布

为了更为详细地对比两种拟合算法，本文计算了两种拟合函数的拟合优度

式中：Xi为原始数据；Xˆi为预测值；Xˉi为原始数据平均值。

如表1所示，SSE与RMSE越接近于0，说明函数拟合越好，数据预测越成功。决定系数R-square与校正后决定系数Adjusted R-square是通过数据的变化来表征函数拟合的好坏，值越接近1说明拟合越好。可以看到本文的拟合算法略胜于混合高斯函数拟合算法。综合考虑本文的拟合算法必然可以带来更好的去模糊效果。

表1 拟合优度对比

由于有理数多项式函数的分母多项式强制函数在梯度值较大值时平滑，所以有效地避免了过拟合现象的发生，从而使得模糊核估计得更准确，减少振铃效应。本文通过集成学习[5-7]，首先利用新的拟合函数进行能量项迭代求得模糊核，然后利用Richardson-Lucy算法[8-9]进行反卷积得到去模糊图像。

3 实验结果与分析

本文选择了人工合成图像与自然拍摄的模糊图像进行实验，进而说明有理数多项式逼近自然图像的梯度分布作为先验约束的有效性。采用峰值信噪比PSNR（Peak Signal to Noise Ratio）和均方误差和MSE（Mean Square Error）这两个指标评估两种约束函数的复原结果。

图4为使用混合高斯约束去模糊的结果和有理数多项式约束去模糊的结果，图4a为清晰图像，图4b为人工模糊图像，其中模糊核是均值为0，方差为5的高斯模糊核，图4c为使用混合高斯约束得到的去模糊图像，图4d为使用有理数多项式约束得到的去模糊图像。在图4c中，平坦的背景区域出现了明显的振铃效应，这是因为在使用混合高斯函数拟合自然梯度图像时，在大梯度值区域出现了过拟合现象，导致模糊核估计不准确，从而使得图像恢复失真，出现振铃。在图4d中，由于使用有理数多项式拟合自然图像梯度，抑制了过拟合现象，所以图像的细节部分保存相对完整，且模糊核估计相对准确，振铃效应减少。

图4 人工模糊图像去模糊效果图

图5 为自然拍摄的模糊图像的去模糊效果图。图5a模糊图像，图5b为使用混合高斯约束得到的去模糊图像，图5c为使用有理数多项式约束得到的去模糊图像。在图5b中，也有明显的振铃效应。而在图5c中，由于使用有理数多项式拟合自然图像梯度，抑制了过拟合现象，振铃效应得到了明显的抑制。

图5 自然模糊图像去模糊效果图

表2为使用有理数多项式约束的去模糊图像与混合高斯约束的去模糊图像的PSNR、MSE比较。从表中结果可以看出，有理数多项式拟合自然图像的梯度分布作为约束在这两项客观评价上有提升，但是在运算速度上，由于算法本身的自然对数限制，所以使用多项式拟合后，迭代所需要的时间更长。

表2 人工模糊图像去模糊效果比较

4 结论

本文提出了基于有理数多项式的图像先验模型约束，利用有理数多项式拟合自然图像梯度分布，通过选取合理的拟合参数，得到拟合优度良好的拟合函数，避免了由于混合高斯函数过拟合现象带来的模糊核估计不准确，从而得到了较佳的去模糊效果。使用人工模糊图像与自然模糊图像的复原结果证明了本文算法的有效性和可行性。

[1]FERGUS R，SINGH B，HERTZMANN A，et al.Removing camera shake from a single photograph[C]//Proc.ACM Trans.Graphics（TOG）.[S.l.]：ACM，2006：787-794.

[2]SHAN Q，JIA J，AGARWALA A.High-quality motion deblurring from a single image[C]//Proc.ACM Trans.Graphics（TOG）.[S.l.]：ACM，2008：73.

[3]KRAHMER F，LIN Y，MCADOO B，et al.Blind image deconvolution：motion blur estimation[J].IMA Preprints Series，2006（21）：33-35.

[4] STEFAN R，MICHAEL J.Fields of experts：freamwork for learning image priors[J].Computer Vision and Pattern Recognition，2005（10）：56-59.

[5]YAIR W，FREEMAN W T.What makes a good model of natural images[J].Computer Vision and Pattern Recognition，2007（8）：14-20.

[6]MISKIN J，MACKAY D.Ensemble learning for blind image separation and deconvolution[J].Neural Computing，2000（9）：123-141.

[7] OSHER S，RUDIN L I.Feature-oriented image enhancement using shock filters[J].SIAM Journal on Numerical Analysis，1990，27（4）：919-940.

[8]MISKIN JW.Ensemble learning for independent component analysis[D].Cambridge：University of Cambridge，2000.

[9] RICHARDSON W H.Bayesian-based iterative method of image restoration[J].JOSA，1972，62（1）：55-59.

[10] LUCY L B.An iterative technique for the rectification of observed distributions[J].The Astronomical Journal，1974（79）：745.