导体电磁散射问题的H2矩阵快速求解算法
2015-10-20黄晓菁南京邮电大学电子科学与工程学院江苏南京210003
黄晓菁(南京邮电大学 电子科学与工程学院,江苏 南京 210003)
导体电磁散射问题的H2矩阵快速求解算法
黄晓菁
(南京邮电大学电子科学与工程学院,江苏南京210003)
根据理想导体的边界条件建立线、面连接结构的电场积分方程。该积分方程运用矩量法直接进行计算时,随着电尺寸增大,计算量和存储量就会迅速增加,进而降低了求解的效率。为了降低计算量和存储量,运用H2矩阵方法的可容许条件将阻抗矩阵元素划分为远区场的矩阵块和近区场的矩阵块。近区场的矩阵块直接用矩量法计算并进行存储,远区场的矩阵块通过H2矩阵的层间插值的方法进行处理并存储,从而有效地降低了计算量和存储量。
MoM;H2矩阵;电场积分方程
0 引言
实际工程问题中,常常遇到线天线与平台相连的情况(例如飞机、轮船、手机上的天线等),于是求解这类的电场积分方程问题具有非常重要的意义。
可是运用矩量法(MoM)[1]直接求解计算该积分方程时,随着目标电尺寸增大,计算量和存储量就会迅速增加,进而降低了求解的效率。随着电磁数值计算的发展,陆续地提出了不少快速算法,例如FMM[2]、MLFMA[3]、CGFFT以及H-Matrix[4-5]等,虽然这些算法中最好的已经能够将计算量和存储量从最初的O(N2)和O(N3)的数量级降低到O(NlogN)的数量级,但是这并不是最理想的情况,当未知量N继续增大时,O(NlogN)的数量级还是很惊人的。于是本文通过结合H2-Matrix[6]算法实现将数量级降低到O(N)线性阶的关系。
1 线面连接结构的积分方程的构建
空间中任意一点的散射电场Es(r)是由线面连接结构的面电流密度Js(r)和线电流密度Jw(r)二者综合作用产生的,表达式为:
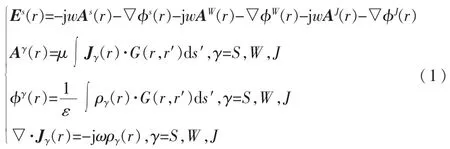
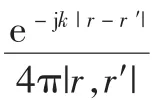
理想导体表面的切向电场边界条件为:

将式(1)代入式(2)得到:

2 H2矩阵求解积分方程
式(3)中的未知量Jγ(r)可以用一组线性不相关的基函数(r)展开,理想导体的表面部分选用RWG基函数[7],导线部分选用三角基函数,而线-面连接点选用连接基函数[8],然后运用伽略金法得到矩阵形式ZI=V的积分方程如下:
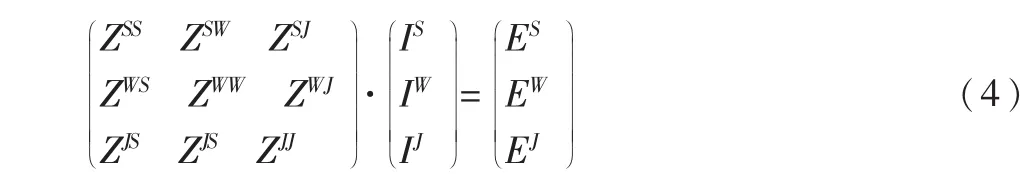
对于式(4)中的阻抗矩阵Z中的元素运用可容性条件[5]将其划分为近区块和远区块。
近区块中的阻抗矩阵元素是不可容的,直接采用矩量法进行计算。
而对于远区块中可容的阻抗矩阵元素运用H2矩阵方法计算。远区块的核函数-格林函数采用Lagrange多项式[9]进行退化核处理。于是式(3)中的核函数G(r,r′)可以写成如下形式:
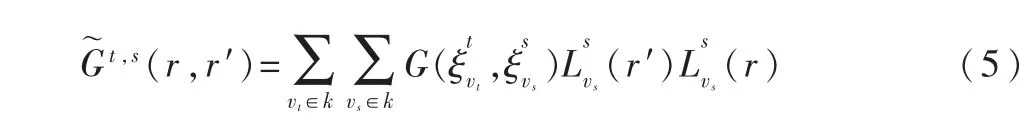
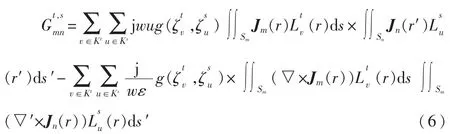
其中,m∈t,n∈s,v∈Kt,u∈Ks。
Gt,s可以写成

其中,Vt∈#t×2Kt,St,s∈2Ks×2Kt,Vs∈?s×2Ks

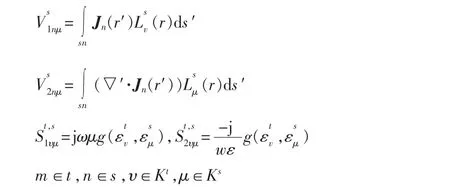

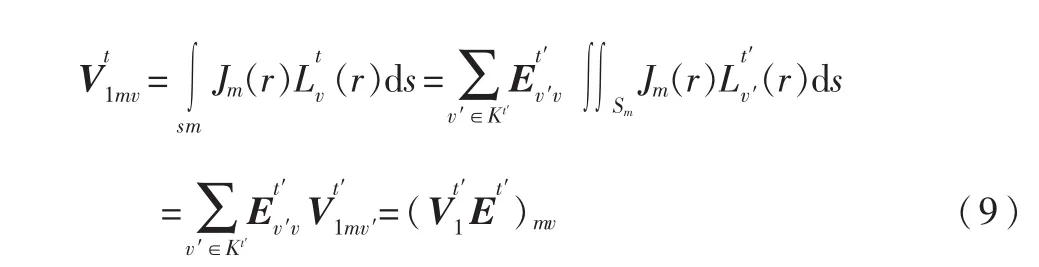
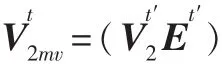
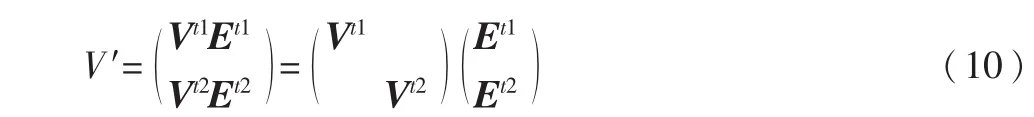
这就意味着只需要存储叶子簇E矩阵Vt并且使用转移矩阵E就可以精确地表示所有的簇树,因为转移矩阵只需要k(t′)k(t)个存储单元,而矩阵Vt需要tgk(t)个存储单元,k(t)=t,因此H2矩阵的嵌套结构有效节省了存储量。从而使H2矩阵的计算量和存储量近似达到线性阶O(N)。
下面就运用存储量小、步收敛性、稳定性高的共轭梯度迭代法[10-12]求解矩阵-向量方程,得出感应电流。
3 数值算例
算例1为了验证矩量法结合H2矩阵方法的正确性,首先计算了频率为300MHz的均匀平面波,它沿θ=0°,φ=0°入射到半径为0.8λ的金属球上,其中散射方向为θ=0°~180°,φ=0°。通过对两种计算方法结果的比较(如图1所示)可以判断出H2矩阵方法的正确性。
算例2电磁波频率f=300MHz,辐射方向为θ=0°~180°,φ=0°,激励采用连接点馈电,分别计算了0.6λ~2.8λ,H2矩阵算法与MoM分别计算时存储量随未知量的变化,以及阻抗矩阵元素计算时间量随未知量的变化,结果如图2和图3所示。从图2、图3可以看出,H2矩阵算法不管是阻抗矩阵元素的求解时间还是总的程序求解时间都明显比MoM要少,并且可以看出H2矩阵算法的计算量随未知量的变化近似呈线性阶O(N)的增长趋势。
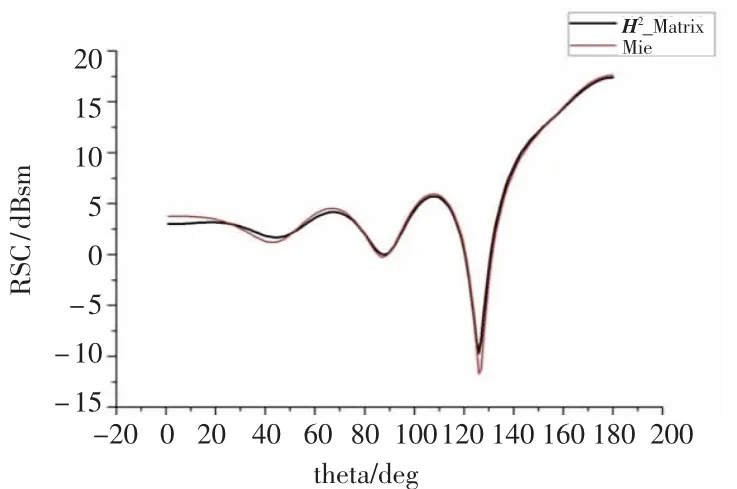
图1 金属球θθ极化双站RCS
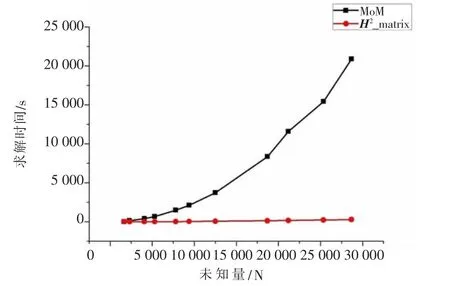
图2 MoM与H2矩阵的矩阵生成时间对比曲线图
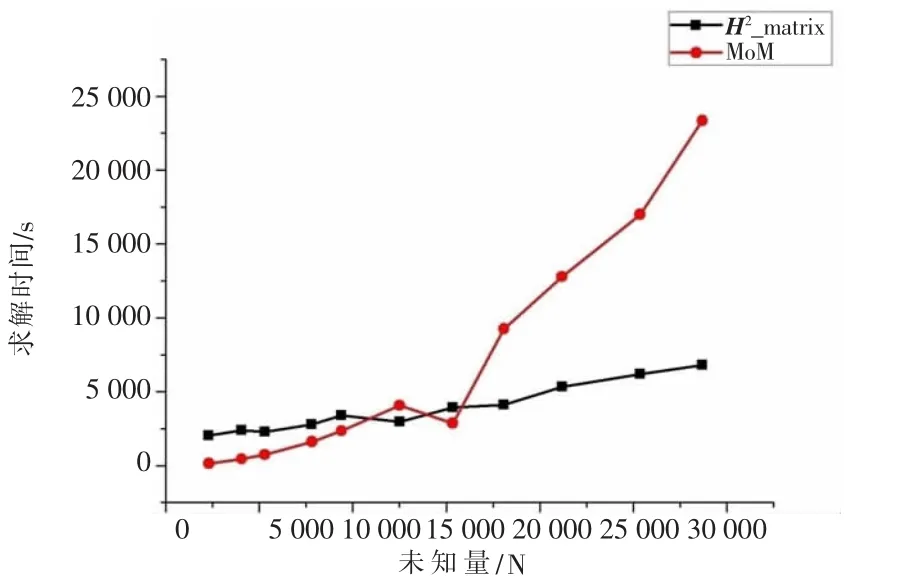
图3 MoM与H2矩阵总的求解时间随未知量变化
图4给出了H2矩阵算法与矩量法求解电场积方程所需存储量随未知量变化的曲线图。由图4可知,MoM计算时所需的存储量随着未知量的变化呈O(N2)的关系迅速增加,而H2矩阵所需的存储量与未知量之间的关系呈线性阶O(N)的变化趋势。

图4 MoM与H2矩阵存计算存储量对比曲线图
4 结论
本文采用H2矩阵算法计算电场积分方程,通过传递矩阵的嵌套方法能够有效地将计算所需的存储量和计算量近似降低到线性阶O(N)。同时H2矩阵算法对模型并没有具体的要求,可以推广到求解任意导体线面结构的模型。
[1]GIBSON W C.The method of moments in electromagnetics[M].CRC Press,2007.
[2]CHENG H,GREENGARD L,ROKHLIN V.A fast adaptive multipole algorithm in three dimensions[J].Journal of Computational Physics,1999,155(2):468-498.
[3]ROKHLIN V.Rapid solution ofintegralequationsof scattering theory in two dimensions[J].Journal of Computational Physics,1990,86(2):414-439.
[4]HACKBUSCH W.A sparse matrix arithmetic based on HMatrices.Part I:introduction to H-Matrices[J].Computing,1999,62(2):89-108.
[5]HACKBUSCH W,KHOROMSKIJ B N.A Sparse-matrix arithmetic[J].Computing,2000,64(1):21-47.
[6]BÖRM S.H2-matrices-multilevel methods for the approximation of integral operators[J].Computing and Visualization in Science,2004,7(3-4):173-181.
[7] RAO S,WILTON D,GLISSON A.Electromagnetic scattering by surfaces of arbitrary shape[J].IEEE Transactions on Antennas and Propagation,1982,30(3):409-418.
[8]HWU S U,WILTON D R,RAO S M.Electromagnetic scattering and radiation by arbitrary conducting wire/surface configurations[C].IEEE Society International Symposium on Antennas and Propagation,Syracuse,NY,USA,1988,2:890-893.
[9]唐松生,隋树林.拉格朗日插值多项式[J].青岛化工学院学报,1992(4):101-105.
[10]王学忠,黄廷祝,李良,等.H-矩阵方程组的预条件迭代法[J].计算数学,2007,29(1):89-98.
[11]郑丽.几种共轭梯度法的研究[D].重庆:重庆大学,2009.
[12]张颖.有关共轭梯度法的一些研究[D].大连:大连理工大学,2012.
An H2-matrix-based method for fast solving electromagnetic problems of perfect conducting surface
Huang Xiaojing
(College of Electronic Science and Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)
In this paper,based on perfect conductor boundary conditions building the electric field integral equation of wire attached to an arbitrary faceted surface.When using the method of moments to calculate directly,with the increasing size of electrical conductor,computation and storage will increase rapidly,thereby reducing the efficiency of solution.In order to reduce the computation and storage,using the permissible conditions of the H2-Matrix to divide the elements of impedance matrix into far field and near field.Matrix block of near field can be calculated and stored directly by using the method of moments,while matrix block of far field can be disposed and stored by method of interpolation between layers of H2-Matrix,thus greatly reducing the amount of computation and storage.
MoM;H2-Matrix;the electric field integral equation
O441.5
A
1674-7720(2015)10-0010-03
201-0-0)
黄晓菁(1990-),女,硕士研究生,主要研究方向:电磁工程计算机辅助分析与设计。
